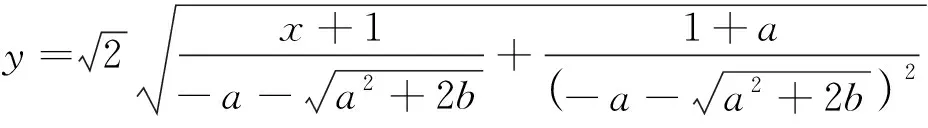一类三次多项式系统的全局分析*
方成鸿
(景德镇陶瓷大学 信息工程学院,江西 景德镇 333403)
关于平面二次多项式微分系统的定性分析,研究结果较丰富,文献[1]有论述,对于三次系统,多为分析不同形式的三次系统,获得系统的结构相图或者极限环存在的条件,以便了解三次系统的各种全局结构.考虑如下形式的系统:
(1)
文献[2]包含c=0时的结论,以下设c=1,否则可作适当的变换达成.本文分析点(a,b)位于第一、三象限的情形,这时系统(1)以(虚)椭圆1+ax2+by2=0为垂直等倾线,通过对奇点、无穷远奇点的讨论,获得了系统(1)的全局结构相图.
1 奇点的性态
方程(1)的右端所定义的平面向量场关于坐标x轴对称,故中心型奇点都是中心.
引理1系统(1)的奇点O(0, 0)是中心.
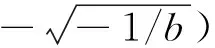
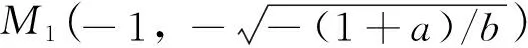

2 关于高次奇点轨线走向的结论
为应用方便,对文献[4]的引理1进行推广.设原点是
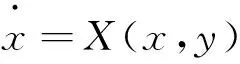
(2)
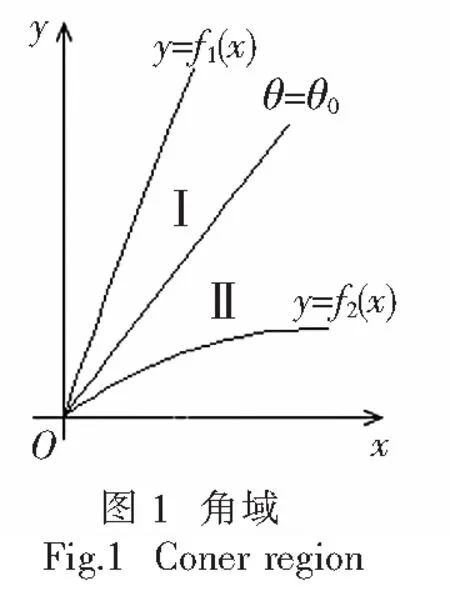
的孤立奇点,其中X(x,y)、Y(x,y)在原点附近具有任意阶偏导数,在原点处的函数值及一阶偏导数值均为零.
定理1如图1,设θ=θ0是特殊方向,曲线l1:y=f1(x)是系统(2)的水平等倾线,角域I内无其他等倾线,如果存在正数c使得当0 上述角域也可位于其他象限,相应修改不等号方向即可.同理可证. 定理2如图1,设θ=θ0是特殊方向,曲线l2:y=f2(x)是系统(2)的垂直等倾线,角域Ⅱ内无其他等倾线,如果存在正数c使得当0 作Poincare变换u=y/x,z=1/x及时间变换dτ=dt/z2,系统(1)化为 (3) 系统(3)的奇点附近的轨线拓扑结构如图2所示. 作变换v=x/y,z=1/y以及时间变换dτ=dt/z2,系统(1)化为 (4) 定理3当a=0时,系统(1)的全局结构相图如图4所示;当b=0时,系统(1)的全局结构相图如图5所示. 引理5当a=-1且-1/2≤b<0时,鞍点B2位于左半平面的不稳定流形以A为ω极限点. 引理6当-1 定理4当a<-1且b<0或者a=-1且b<-a2/2时,系统(1)的全局结构相图如图6(1)所示;当a=-1且-a2/2≤b<0时,系统(1)的相图如图6(2)所示;当-1 引理7当-1 引理8当-1 引理10当-1 由于div(P,Q)=-2axy,可知a≠0时在任何一个象限,系统(1)都不存在闭轨线.根据引理9、10、11,结合无穷远奇点的性态可得. 定理5设-1 关于ab<0的情形,另文分析,这时系统(1)的一条垂直等倾线是双曲线1+ax2+by2=0.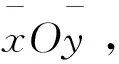
3 无穷远奇点
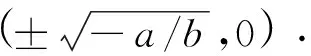
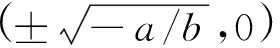

4 全局结构