电感材料与电流限制相关性认知诊断模型研究*

吴俊锋， 旷 怡， 李 辉， 段 斌， 于立君， 章 兢

(1.湘潭大学 信息工程学院，湖南 湘潭 411105；2.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

《华盛顿协议》作为目前世界工程教育认证领域最具权威性的国际工程师互认协议，提出工程教育专业不仅要深入理解和把握复杂工程问题，更要培养学生具有解决复杂工程问题的能力[1].要求掌握专业知识，能够灵活运用各种现代工具和技术进行系统设计与开发，对复杂工程问题进行相关研究.因此，如何对学生专业知识和技能的掌握情况进行有效的评估，已经成为当前的重要研究问题.

传统的评估方法存在效率低，主观性强的问题，并且不能对学生进行个性化评估.随着互联网教育的迅速发展，实现了以现代统计方法和计算机技术作为工具实现诊断学生的认知结构和认知过程[2].教育评估方法的形式多种多样，不同的方法会有不同的产出结果，有些模型是在统计的基础上发展起来的，有一些则注重证据的获取.目前常用的模型类型有：潜在特质模型(latent trait models, LTM)[3]、证据中心设计(evidence centered design, ECD)[4]、潜在分类模型(latent class models, LCM)[5]等.

基于贝叶斯心理测量的评估方法对学生知识点的掌握程度进行建模分析，它能够用合适的粒度(即考察点的细分或细化程度)对问题解决进行简化描述，界定测量建构，设计测验项目，进行建模分析和解释[6].与此同时，它能够挖掘学生的潜在认知状态(如知识点掌握程度等)，解释和预报学生表现, 以及他们在这个领域中认知上的不足.

本文以降压稳压器中电流限制功能为背景，研究电流限制与电感类型之间的相关性为例，评估学生对电流限制复杂工程问题研究的能力，阐述电流限制认知的局限性.首先，基于认知诊断模型构建熟练度模型、任务模型以及证据模型，依据项目反应理论对模型中变量间的关系进行了估计；其次，随机选取两位被试者，要求对电气工程领域“电感饱和与电流限制相关性”的复杂问题进行研究，通过设计实验，分析与解释数据，并通过信息综合得到合理有效的结论；最后,利用BNs分析软件Netica，构建电流限制功能认知诊断系统，以被试者的实验结果作为数据，推断出模型中潜在变量的等级的概率，通过案例分析的结果验证所述方案的准确性和可行性.

1 电流限制功能的认知局限

降压稳压器广泛用于工业和基础设施应用，可将12 V电源轨步降至适合微控制器、FPGA、内存和外设I/O的负载点输入，最小可低至0.6 V.为防止这些开关稳压器由于过量电流而损坏，电流限制功能起到关键性的作用[7].

电流限制功能的激活受控于平均负载电流以及电感电流纹波峰-峰值，进而又取决于电感的输入电压Ui、开关频率fs、占空比D二极管压降Ud和电感.因此，在对电路中电流限制功能的解决方案中，需要考虑以下几点.

1.1 常规参数设计

(1) 根据周期内电流是否为0开始和电感电流是否为0开始，可以将电源电路的工作状态分为电流连续模式(CCM)和电流非连续模式(DCM)两种情况：

① CMM：电感上连续有导通电流，电感电流不会降低到0，而是保持连续，根据电路拓扑图，此时输入输出电压关系为

U0=DUi,

(1)

式中，D为开关控制信号的占空比UOUT.由于电感电流不为0，因此工作周期中，电路仅有两个工作状态：导通或者截止.在功率开关管导通的情况下，电感电流会从某个大于0的初始值增加到最高值，最终的结果使得在截止期间提供给负载的电流得到补充.电感两端的电压为

UL(t)=Ui-U0(t) .

(2)

电感电流纹波峰值为

(3)

在开关管截止期间，由于电感电压极性方向，二极管导通，电路形成新的回路，电感发出能量提供给负载，电感电流减小至初始值，此时，电感电压为：

UL(t)=-U0(t)，

(4)

此时电感电流为

(5)

当t=Ts时，式(5)可以化简为

(6)

当电路处于稳定时候iL(Ts)=iL(0)，

(7)

② DCM：当电感值小于临界值时，流经电感的电流就会处于不连续的状态，此时电路会达到伏秒平衡，有

(Vi-V0)D1=V0D2.

(8)

根据欧姆定理，可以推出电感电流为：

(9)

式中，D1为时间从0到t1的与空比，D2为t1到t2的与空比.

(2) 开关频率计算

更高的开关频率可以增大电流限制水平，因为电感电流纹波的幅度会更小，然后在给定负载电流的情况下控制电压电平将更小.根据BUCK电路中频率设定的频移保护，开关电源的频率应当小于ffsp.

(10)

式中：RdL为电感电阻；IL为电感电流；RD(ON)为导通电阻；UIMAX为最大输入电压；UOUT为输出电压；USC为短路输出电压；tON为导通时间.

(3) 输出电容参数计算

较大的输出电容会产生较低的输出电压纹波，从而会增大电流限制水平.电流限制对输出电容大小的敏感性取决于电压环路增益穿越频率[8].使用具有高带宽特征的误差放大器可实现高穿越频率.

对于高滤波电容，电压纹波ΔU0取决于输入电容等效串联电阻ESR，和电流纹波Δipp，

ΔU0=ESRΔiPP.

(11)

对于低滤波电容，输出电压纹波为

ΔU0=Δipp/8fzCout.

(12)

电压环路增益为

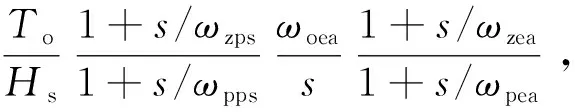
(13)

式中，

(14)

式中：gmps表示PCC降压稳压器的跨导，{Rg,Ri}为电压传感器，{Cf1,Cf2,Rf2}是反馈阻抗.

1.2 电感磁芯材料选型

在常规电感元件的设计中，一般设计人员在分析电感电流纹波峰-峰值时，认为电感L为恒量.然而，随着电流增大，电感可能在高电流时饱和，而饱和时不同磁芯类型的电感其电感值减小的程度不同，从而影响电感电流纹波峰-峰值[9].

因为不同的磁芯材料具有不同的饱和特性，电感量随电感电流变化的幅度会不同.其中，铁氧体磁芯电感的动态电感量随电流的变化为

(15)

式中：Ld为动态电感量；Lnom是静态电感量，即电感标称值；Lsat为深度饱和时的电感量；系数σ由电感类型，磁芯材料和温度决定.

磁粉芯电感的动态电感量随电流的变化为

(16)

式中：L30%是满足L(I30%)=0.7Lnom条件的30%饱和电流.

根据式(15)和式(16)，铁氧体磁芯的电感在小电流的条件下电感量变化不大，而在大电流的条件下，因磁芯的急剧饱和作用使得电感量迅速下降，磁粉芯电感的电感量随电流的增加，呈线性的方式下降.

对于不饱和的电感，其纹波电流峰-峰值表示为

Δipp=Vout(1-D)/(fsL)，

(17)

其中，输入电压和开关频率对电感电流纹波有很大影响.

对于饱和的电感，其纹波电流峰-峰值会比不饱和电感情况下要大，

Δipp>Vout(1-D)/(fsL).

(18)

2 贝叶斯心理测量模型

2.1 能力模型

基于电源电流限制工程问题特征构建能力模型，表示电感特性参数、磁芯材料知识与电感频率特性等潜在变量之间的关系.节点之间的有向连接线表示节点之间的相互关系，方框为似然概率，表示子节点与父节点之间的关系，每一个节点都有一组不同于其他节点的状态值，表示该节点知识或认知能力的掌握程度.电流限制功能中电感元件能力模型如图1所示.

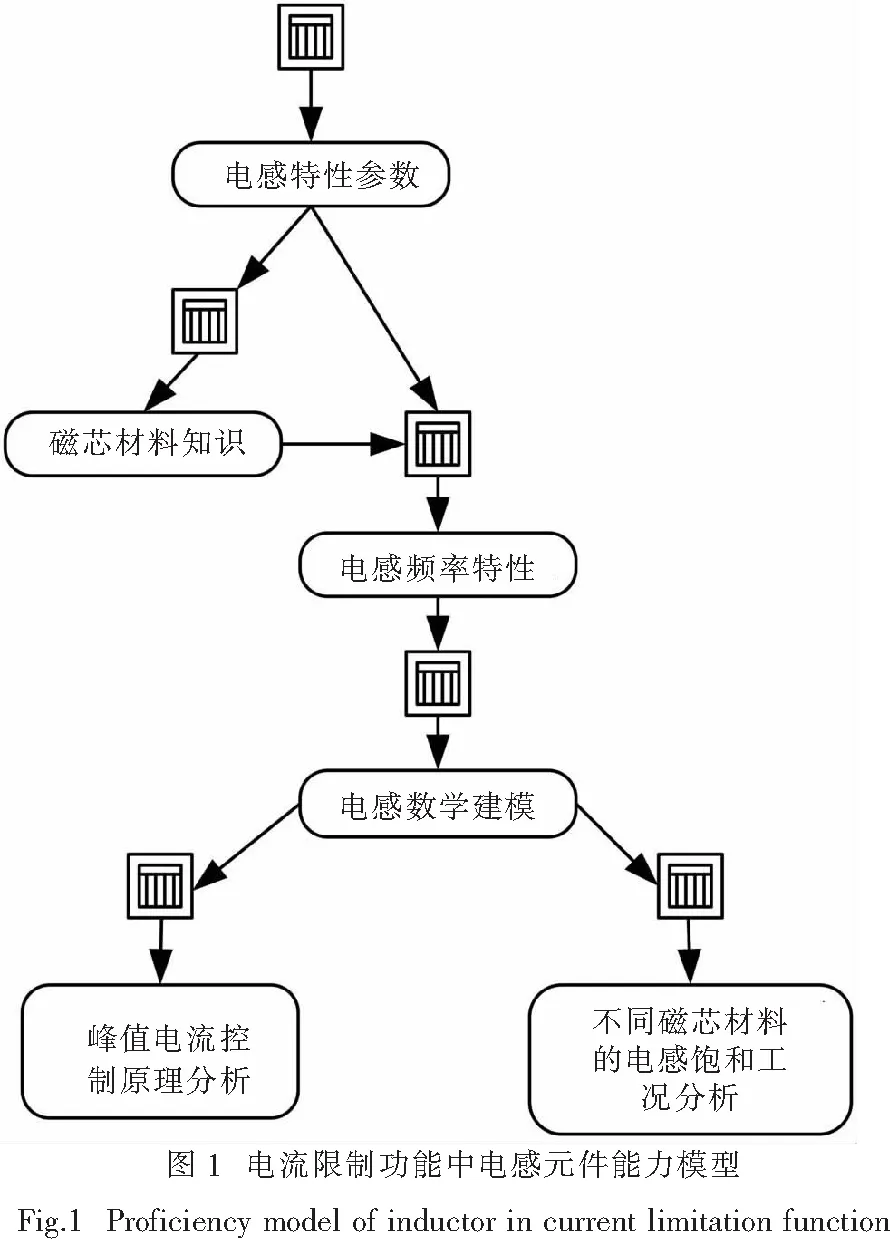
电感特性参数包括：电感量L，感抗XL，品质因素Q，分布电容，标称电流，允许误差.

电感频率特性表示：在低频时，电感表现出储能、滤高频的特性；在高频时，电感表现出明显的阻抗特性，消耗能量并转换为热能，并且不同磁芯材料电感的高频特性不一样.

2.2 任务模型

“电感饱和与电流限制相关性”是电气工程的一个复杂问题，学生就能够基于科学原理并采用相应科学方法对电气工程领域“电感饱和与电流限制相关性”的复杂问题进行研究，通过设计实验，分析与解释数据并通过信息综合得到合理有效的结论。具体任务包括：

(1) 依据降压稳压器的控制原理，分析影响电流限制需要获取的电路参数，并设置输入电压，开关频率，输出电容及电感.

(2) 根据电感特性参数，在不同磁芯材料的电感下，建立电感量与电感电流的数学模型，如式(15)和式(16)，计算最大输出电流.

(3) 设计实验，使用铁氧体和磁粉芯电感与不同输入电压来运行降压稳压器时的控制电压和最大输出电流.

(4) 使用铁氧体电感以及不同输入电压、开关频率和输出电容设置来运行降压稳压器时的控制电压和最大输出电流.

(5) 观测在低电流和高电流时的电感电流纹波，绘制磁粉芯与铁氧体电感在不同电流下的变化曲线.

(6) 对比并分析实验结果，得出允许最高电流限制的电感，并分析不同的开关频率和输出电容对电流限制的影响.

2.3 证据模型

证据模型确定了电力电子器件的认知能力与电源电路认知能力之间的联系，通过电路中的可观测数据，为能力模型提供数据依据.

其中，电感认知能力变量与阻抗认知能力变量间为联合关系.驱动电路认知能力变量、反馈控制电路认知能力变量和其他综合电路认知能力变量，三个变量之间均为补偿关系.

结合被试者的操作过程的有效性、实验结果的正确性和数据分析的合理性，领域专家对被试者每个观测变量的实验结果评分，依据各个可观测变量的得分对电感电流限制认知能力以及电感磁芯材料认知能力进行贝叶斯推断.

2.4 贝叶斯推理

心理测量学理应是心理与测量学的结合,是心理学与测量学的交叉学科，它的本质在于根据被试者在某些观测指标(如测验项目)上的反应对其在测验所要测量的某种心理属性上的状态或程度进行推断和标定.

等级反应模型是心理测量模型中常用的潜在特质模型.GRM中每个任务有不同的难度等级，而且每个任务各个等级上的难度值是严格单调递增的.项目用函数表示为

(19)

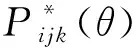
(20)

采用有效θ方法，引入参数c与d，以生成一个用于单参数GRM的变量，记作θ**.设子变量只受单一父变量θ1的影响，经过线性变换，自变量有效θ可表示为

θ**=c×θ1+d.

(21)

依据任务模型得到的实验结果和分析，经过贝叶斯推理得到知识与认知能力掌握程度的概率，即

(22)

式中：θ表示潜在变量；X表示可观测变量；p(θ)指潜在变量的先验概率；p(X)指θ在所有可能取值的情况下，可观测变量X的概率的期望；p(X|θ)为似然概率，表示潜在变量在已知的情况下，可观测变量的可信度；p(θ|X)表示在观测到具体的实验结果和分析后，潜在变量的概率，即后验概率[10].

3 变量间似然概率生成及变量间的关系

3.1 能力模型中变量间的关系

(1) 直接依赖关系

在图1中，子节点与父节点是依赖关系的包括：磁芯材料知识(CMK)与电感特性参数(ICP)；电感频率特性与电感数学建模；峰值电流控制原理分析与电感数学建模；不同磁芯材料的电感饱和工况分析与电感数学建模.其中，变量CMK的有效θ表达式为

(23)

(2) baseline-ceiling关系

在图1中，电感频率特性变量(LFC)，与两个父变量电感特性参数知识(ICP)与磁芯材料知识变量(CK)之间是baseline-ceiling关系，其有效θ表达式为

(24)

(25)

3.2 证据模型中变量间的关系

(1) 联合关系

在图2不同磁芯材料的电感饱和工况分析证据模型中，子节点不同磁芯材料的电感饱和工况分析&电感工作原理变量(SA&IK)与父节点不同磁芯材料的电感饱和工况分析SA和电感工作原理变量IK之间为联合关系，其有效θ表达式为

(26)

(27)

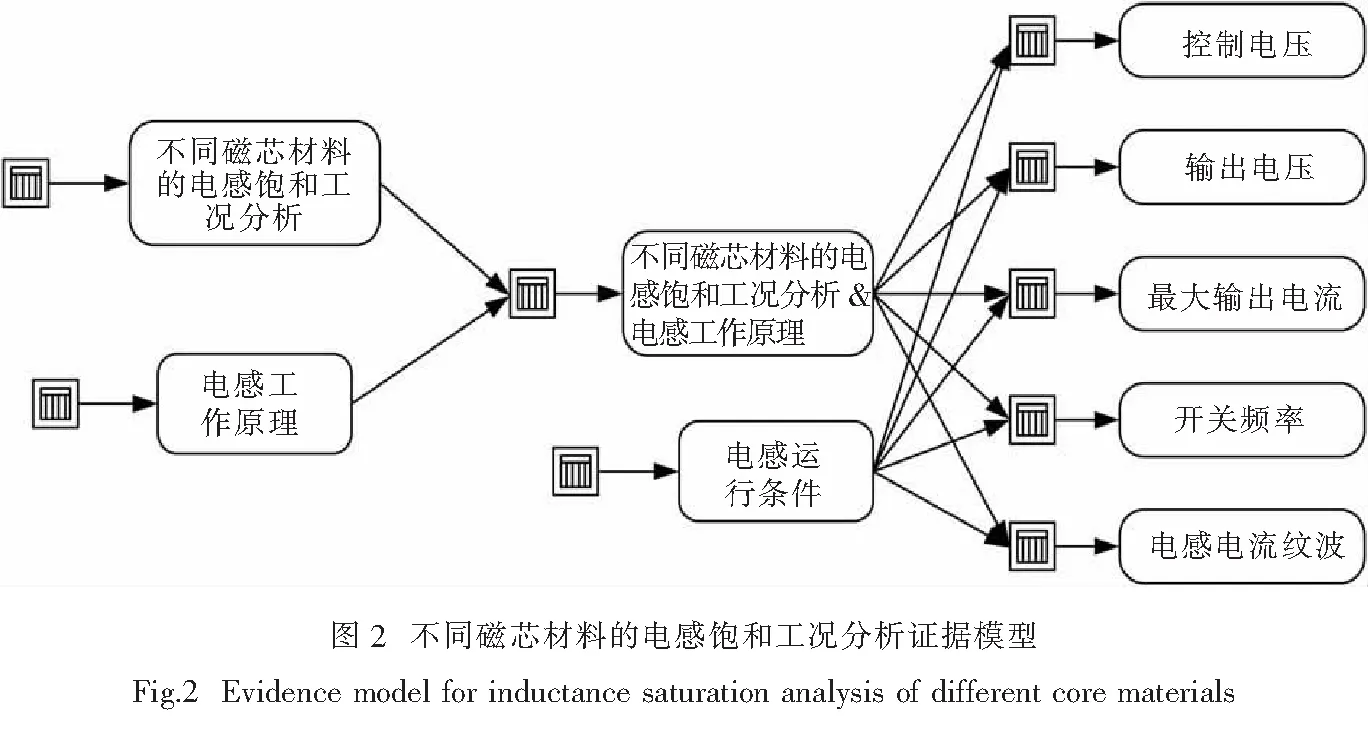
同理，在图3峰值电流控制原理分析证据模型中，子节点峰值电流控制原理分析&电感数学建模(PCC&IMM)与两个父节点峰值电流控制原理分析(PCC)和电感数学建模(IMM)直接为联合关系.

(2) 补偿关系

在图2电感饱和工况分析证据模型中，电感运行条件变量是外生变量，是对电感运行场景的描述.控制电压、输出电压、最大输出电流、开关频率和电感电流纹波为可观测变量(OB).可观测变量与父节点不同磁芯材料的电感饱和工况分析&电感工作原理变量(SA&IK)和电感运行条件之间为补偿关系，其有效θ表达式为

(28)

同理，在图3峰值电流控制原理分析证据模型中，可观测变量与父节点峰值电流控制原理分析&电感数学建模(PCC&IMM)和电感运行条件之间为补偿关系.

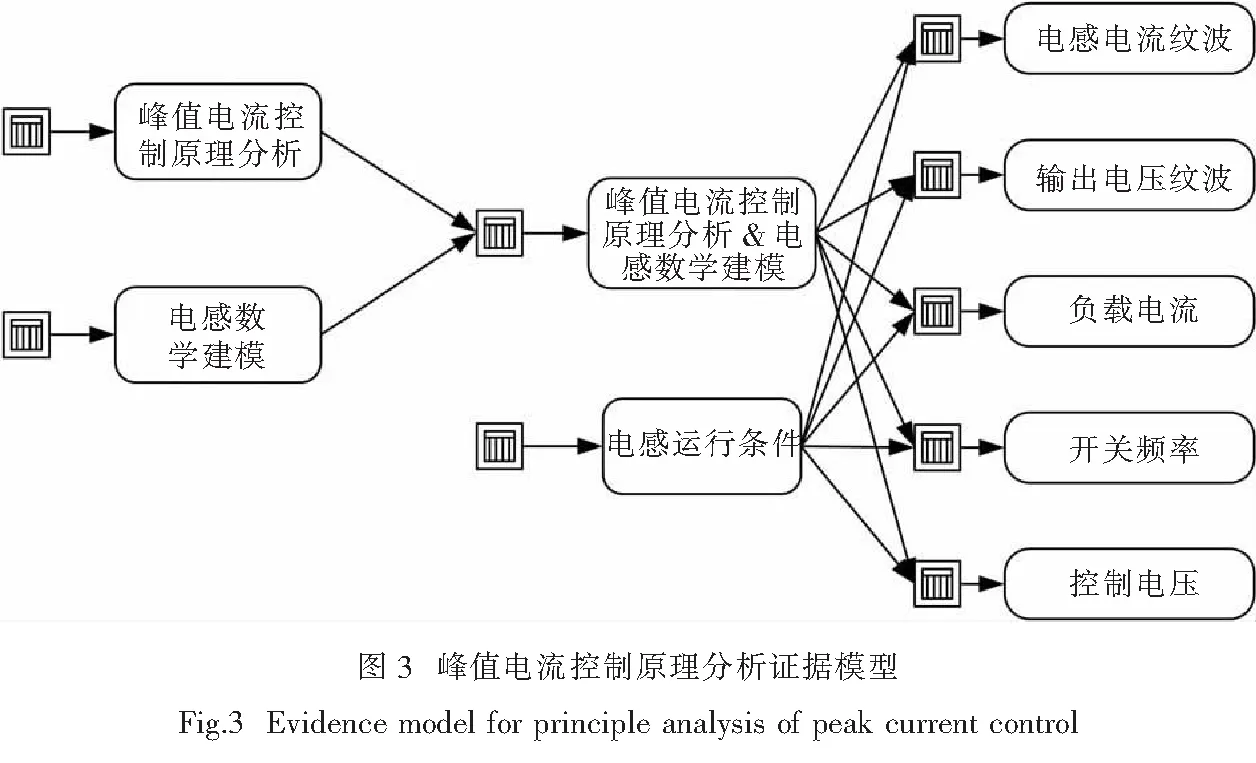
4 电流限制功能认知诊断系统

4.1 条件概率生成

依据电力电子学科知识和领域专家意见，选取能力模型和证据模型中参数c、d，并且不同变量关系的参数c、d不同，不同变量间的参数c、d也不同.

(1) 在能力模型中，父节点电感特性参数知识(ICP)与子节点磁芯材料知识变量(CK)是直接依赖关系，变量间的条件概率如表1所示.其中，cCMK,ICP=2.8，dCMK,ICP=-5.4.

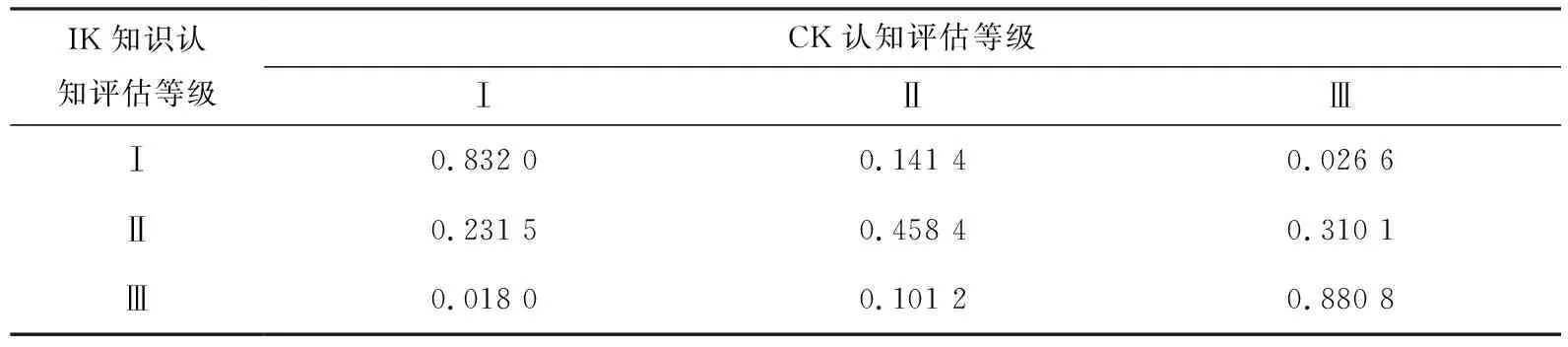
表1 磁芯材料知识变量条件概率表

(2) 在能力模型中，两个父变量电感特性参数知识ICP与磁芯材料知识变量CK与子节点电感频率特性LFC之间是baseline-ceiling关系，似然概率如表2所示.其中，cIFC,baseline=1.7，cIFC,compensatory=1,dIFC,baseline=-3.8.

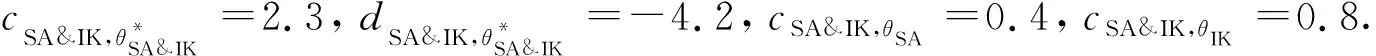
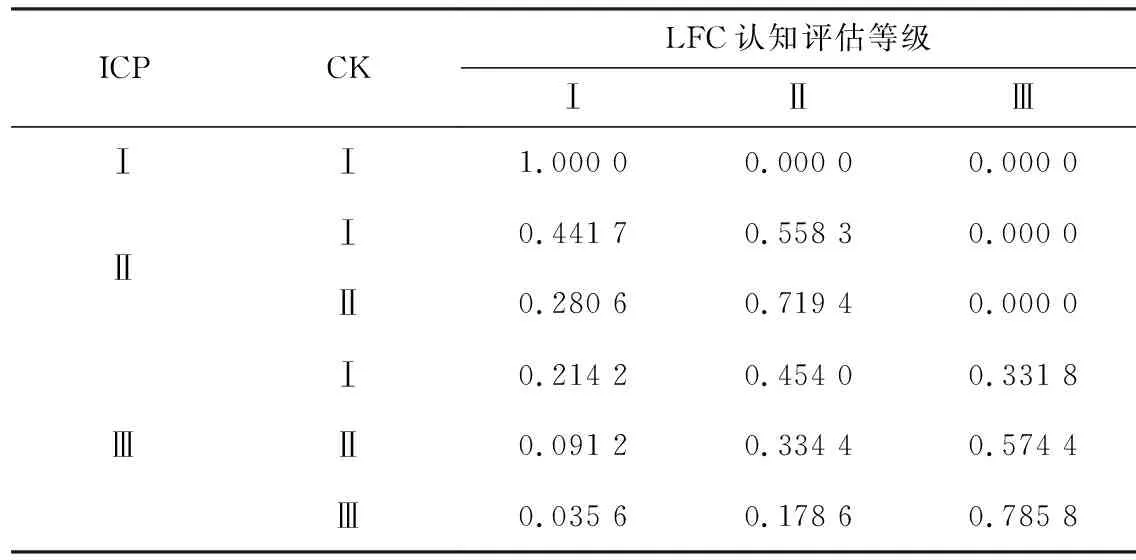
表2 电感频率特性变量条件概率表

表3 不同磁芯材料的电感饱和工况分析&电感工作原理变量条件概率表

4.2 案例分析

从某大学18级电气工程专业研究生中抽取两位被测者进行测试，他们分别来自2014级电子信息工程和通信工程本科专业，研究电感磁芯饱和如何影响降压稳压器的电流限制，基于电感工作原理、饱和工况等科学原理设计实验，测量控制电压、最大输出电流等实验数据，分析并解释数据，得出合理有效的结论.对被试者A和B两者设计方案，实验数据与理论值进行比较，将不符合理论值的可观测量视为不合格.被试者实验结果如表4所示.

表4 被试者测试结果表

利用贝叶斯网络分析软件Netica，经贝叶斯网络推理得到被试者A、B的电感饱和工况分析能力的先验与后验概率表，如表5所示.

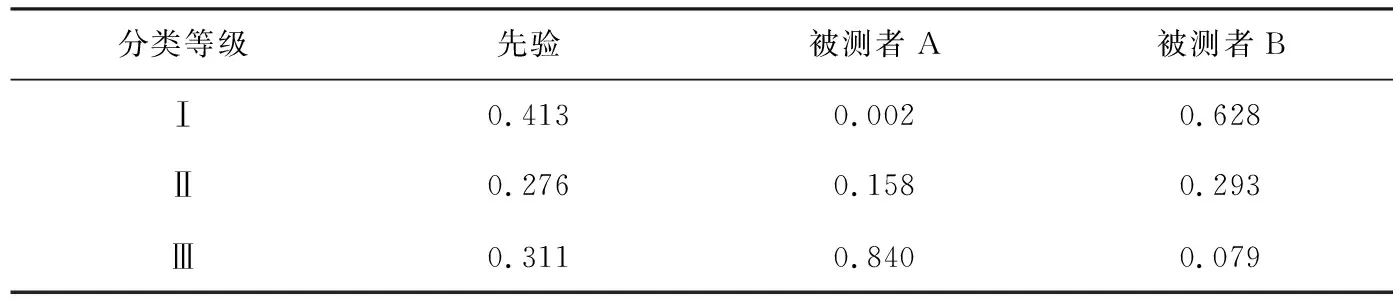
表5 被试者峰值电流控制原理分析能力的先验与后验概率表

其中，被试者A和B的峰值电流控制原理分析能力认知诊断系统如图4和图5所示.

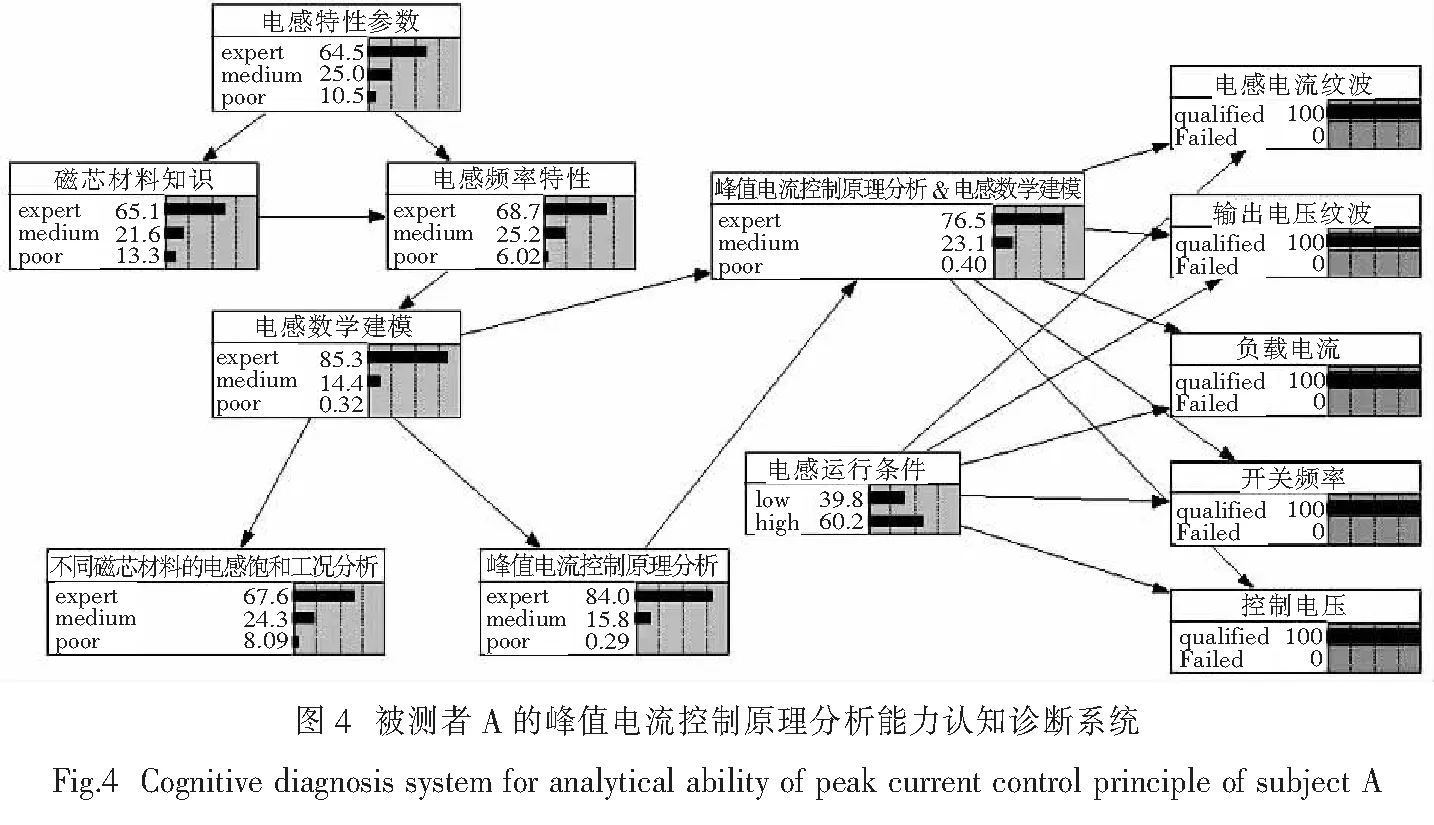
由图4可知，被试者A其峰值电流控制原理分析能力运用熟练度为Ⅰ、Ⅱ、Ⅲ的概率分别为0.29%，15.8%，84%.因此，该被测者的峰值电流控制原理分析能力掌握程度较好.

由图5可知，被试者B其峰值电流控制原理分析能力运用熟练度为Ⅰ、Ⅱ、Ⅲ的概率分别为7.97%，29.3%，62.8%.因此，该被测者的峰值电流控制原理分析能力存在不足，需要加强学习.

5 结论与展望

(1) 根据降压稳压器电流限制中的影响因素，阐述了电流限制认知的局限性.

(2) 结合专家知识，构建了用于评估被试者电流限制功能研究能力的能力模型、任务模型和证据模型，并采用等级反应理论对认知诊断模型中变量间的概率关系进行了计算.

(3) 利用贝叶斯网络分析软件Netica，搭建了电流限制功能研究能力评估系统，并进行了仿真实验，案例分析结果表明了所提方法的正确性和有效性.

(4) 基于认知诊断理论的能力评估方法可扩展应用到其他工程专业领域，具有普适性.