智能车竞赛学习成果认知诊断模型*

罗新宇， 陈洋卓， 段 斌， 张 佐， 章 兢

(1.湘潭大学 信息工程学院，湖南 湘潭 411105；2.清华大学 自动化系，北京 100084)

智能车竞赛是一个集机械、电气、仪器仪表、电子、计算机、控制等多学科综合贯穿始终的面向全国大学生的具有探索性的工程实践活动，是教育部倡导的大学生科技竞赛之一.该竞赛旨在促进高等学校素质教育，培养大学生的综合知识运用能力、基本工程实践能力和创新意识[1].国内外关于学科竞赛学习成果评价的研究很少，文献[1]分析了复杂工程问题的特征和解决复杂工程问题的能力,对每一个指标点设置不同的考核方式来阐述评价学生解决复杂工程问题的能力，但是相对烦琐；文献[2]从系统设计类课程层面,培养学生解决复杂工程问题的能力,阐述数据库系统设计课程的具体教学实践,包括课程内容、课程组织和能力达成评价方法[2]；文献[3]对比赛任务和规则、信号处理所起的作用以及建立在比赛基础上的课程进行了概述[3].如何以学生为中心，围绕学生制定培养目标，按照毕业要求配备合格的师资，评价学生是否具有解决复杂工程问题的能力已然成为一大挑战.智能车在执行任务的过程中运用了多学科知识和个人技能，学生充分运用书本所学原理、公式、方法，结合个人技能，从最开始的方案制定到比赛运行，实际上是解决一系列复杂工程问题.根据智能车竞赛规则，定义所希望测量的知识、能力和技能，结合贝叶斯网络，综合智能车竞赛所体现的学生知识和能力与毕业要求能力的相关关系，构建智能车竞赛学生知识与能力认知诊断模型.通过观察可观察量和认知诊断系统的反馈，对学生知识的掌握程度和个人技能进行评估.

1 智能车竞赛学习成果评价

智能车竞赛学习成果评估整体框架如图1所示，智能车竞赛需运用电气、仪器、机械、电子、计算机、控制等多学科知识综合[4].整个完成过程涉及构思、设计、实施和运行等模块，这些模块具体通过方案制定、理论研究、系统设计、仿真计算、软硬件设计、系统组装与调试等过程证据体现.通过观察运动性能、路径规划、路径识别、参数调整等中间量，作为证据支撑认知诊断模型，经过模型的层层反馈，输出知识和能力熟练度以及所达成的部分毕业要求能力指标点.

学生倾向于以考试为导向的技能，有足够的动力去学习和创新，获得在团队环境中解决真实的工程问题的机会.智能车竞赛从构思、设计、实施到运行，实际上是解决一系列复杂工程问题的过程.基于12条毕业要求指标，对智能车竞赛能力概念化分析，以ECD(evidence-centered design)为理论指导[6]，根据智能车竞赛过程，设计任务模型与结果数据.智能车竞赛展现的能力对应的毕业要求能力指标点如表1所示.

表1 复杂工程问题与智能车的等价性

2 贝叶斯网络应用

2.1 贝叶斯网络的适应性

为了解学生参加智能车竞赛相关知识的掌握程度和能力的强弱，以及毕业要求能力达成情况，以贝叶斯网络为基础，构建认知诊断模型.贝叶斯定理即条件概率推理过程，贝叶斯公式如下：

(1)

其中：p(A|B)称为后验概率，即更新数据后，A事件发生的概率；p(A)称为先验概率，即在得到新数据前事件A的概率；p(B|A)是似然度，在事件A发生的情况下，事件B发生的概率；p(B)是标准化常量[8].

贝叶斯网络主要由三部分组成：有向无环图、先验概率、条件概率[9].有向无环图由节点Di=(Di1,Di2,…,Din)和有向线段L组成，节点Di表示贝叶斯网络节点变量，包括父母节点，子节点，每个节点变量有一个或多个状态Sj=(Sj1,Sj2,…,Sjm).有向线段L连接父节点Di与子节点Di+1，表示父子节点间的依赖关系；先验概率p(Di)是在得到新数据前该节点变量的概率，通常由历史数据决定；条件概率p(Di|Di-1)，即用概率估计的形式表示父节点与子节点之间的关联程度，在同一个父节点下，每个子节点间相互独立，即

p(D1,D2,…,Dn)=∑p(Dn|D1,D2,…,Dn-1)…p(D2|D1)p(D1) .

(2)

2.2 先验概率

在贝叶斯网络中，先验概率的选择一直饱受争议.先验概率分两种：第一种客观先验，例如扁平先验，每一种可能状态赋以相同的权重；第二种主观先验，根据历史数据或专家经验，表达个人对先验的看法[10].常用的先验概率分布有Gamma分布、Beta分布、高斯分布等.智能车竞赛认知诊断模型每个节点变量分为4个状态Sj=(Sj1,Sj2,Sj3,Sj4)，并把等级转换成数值，对这些数值进行分类：S1优秀(90～100)、S2良好(75～89)、S3中等(60～74)、S4不及格(60分以下).

2.3 条件概率

2.3.1层次分析法AHP专业知识和专家经验的引入是公认的降低模型内在不确定性的最佳解决方案，所以被认为是确定CPT(条件概率)的一种重要手段.层次分析法(analytic hierarchy process， AHP)原理即从专家(评分老师)知识经验中训练条件概率信息的贝叶斯网络建模方法[11].

表2 专家决策标准

(1) 识别框架.Θ表示节点Nr的所有可能状态概率取值的一个集合，且Θ内的各种状态互不相容.

(2) 分配函数、焦元.定义m：2Θ→[0，1],若满足如下条件：

(3)

称m(Di)为Θ上的基本概率分配函数，若m(Di)>0，则称A为m的焦元.

(3) 专家决策标准.专家Ek在属性Cx下推断的相关度矩阵：

表3 专家Ek在属性Cx下推断的相关度矩阵

(4)

专家根据对应事件对识别框架的关联程度来给出决策标准.

2.3.2Pert分布Pert分布是一种特殊的Beta分布，存在三个参数：最小值a、最可能值b与最大值.

Pert(a,b,c)=Beta(α1,α2)*(c-a)+a,

(5)

3 证据模型

3.1 路径识别证据模型

由于篇幅有限，以智能车竞赛路径识别环节为例.基于复杂工程问题的特征，对路径识别环节任务执行过程进行归纳.

(1) 工程原理的深入运用和分析.

① 数据采集.将赛道信息以数字量的形式输入单片机.

② 数据处理.对采集到的信息进行处理，去噪声干扰，滤波分析，路况特征提取.

③ 数据控制.控制算法，需要结合道路元素设计合理方案.

④ 使用现代工具、传感器分析和仿真软件的使用.

(2) 涉及多方面的技术，工程和其他因素的分析和综合运用，以及相互间冲突的解决.

① 线性调压、PWM调制与接口电路设计.

② 如何设计传感器接口电路与后续有关电路联系起来.

③ 传感器的输出与计算机的匹配问题，选择器件的问题等.

(3) 创造性抽象模型的建立.

① 数据处理.图像识别存在建模和模式识别.

② 控制本身是基于模型的控制过程.

(4) 非常规方法的提出和运用.

① 不连续道路线和路口的道路元素的识别必须依靠某种策略.

② 电感传感器的温度系数需做大量实验寻找规律和最佳工作点.

(5) 非标准情况或非规范情况的解决.

车模在高速运动过程中，所采集的图像一定有各种非标准情况，对于图像的处理过程也一定有其独特的方法.

(6)问题相关各方利益冲突的调和与解决.

① 车模的运行精度与速度有矛盾，车模的稳定性与速度有矛盾.

② 团队成员的评分.

(7) 综合性分析问题的分析与解决.

运行速度控制知识、传感器知识、转向控制知识等多学科知识的综合.

在内、外部技术问题上进行证据划分，证据部分或全部地支撑了毕业要求能力指标1～5条和11条，对应于复杂工程问题的特征，可对智能车路径识别完成过程中的证据性总结为：

(1) 智能车竞赛路径识别环节设计工程原理的深入运用和分析.

(2) 涉及多方面的技术、工程和其他因素的分析和综合运用，以及相互间冲突的解决.

(3) 数据处理与控制创造性抽象模型的建立.

(4) 非常规方法的提出和运用.

(5) 非标准情况或非规范情况的解决.

(6) 问题相关各方利益冲突的调和与解决.

(7) 车模综合性分析问题的分析与解决.

而对于9，10，12条面向从事解决复杂问题学生应具有的社会能力，我们可以在整个智能车完成过程中罗列新的证据.

(8) 个人与团队的交流和合作.

① 在组建竞赛队伍时，团队成员和指导老师通常来自不同一级学科，不同的专业.

② 团队成员进行互评打分，路径识别环节设计时体现团队协作能力.

(9) 就复杂工程问题与业界同行和社会公众进行有效沟通和交流.

① 在参加比赛的过程中，会与来自其他学校的不同队伍、指导老师进行经验和技术上的交流.

② 比赛完成后，通常需要撰写内容翔实的技术报告，总结整个比赛过程.

根据上述内容，构建节点变量路径识别证据模型，如图2所示.

3.2 路径识别认知诊断模型

路径识别是智能车竞赛设计中的一个重要部分，也是体现学生知识和能力的一个重要节点.根据图2证据模型，对路径识别进行展开，图3为路径识别认知诊断模型.

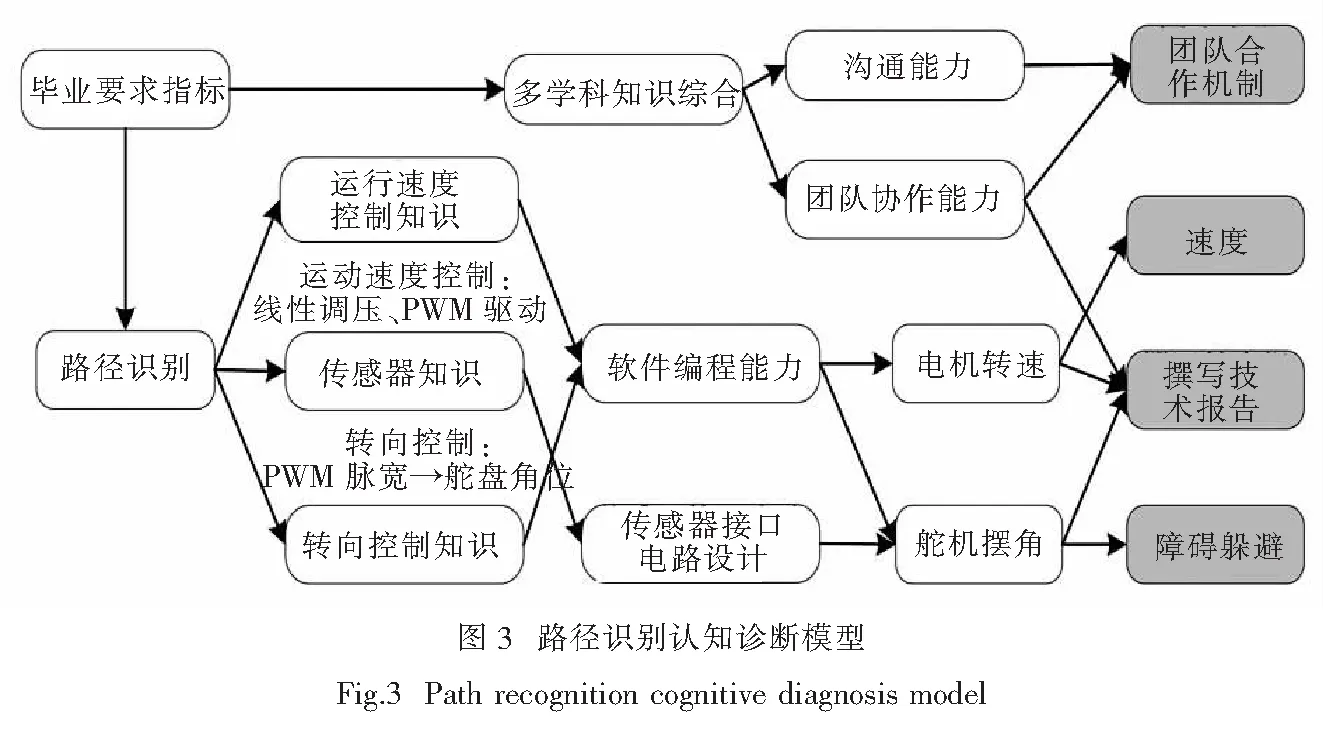
路径识别包括三部分：数据采集，数据处理，数据控制[14-15].路径识别认知诊断模型涉及计算机、控制、电子、电气、仪器仪表等多学科知识综合.具体来说，线性调压、PWM驱动控制运行速度；转向控制知识，即PWM脉宽调制控制舵盘角位来控制智能车运动方向[7]；利用传感器和电路知识，设计传感器接口电路；利用摄像头采集赛道路径图像信息或用传感器采集赛道信息，对数据进行处理和特征提取，编写程序控制电机转速和舵机摆角[7]；最后对团队合作机制、速度、撰写技术报告、障碍躲避等可观察变量进行测量，通过认知诊断模型反馈学生在路径识别这一模块的熟练度和相关知识掌握程度以及能力强弱.

3.3 证据辨识规则

学生参加智能车竞赛既是培养学生解决复杂工程问题的能力，也是培养学生高阶思维能力的过程.高阶思维能力包括问题解决能力、元认知能力、团队协作能力、沟通能力、创造性思维能力五个子能力，问题解决能力与其余四个子能力成正相关，团队协作能力与沟通能力成正相关，与创造性思维能力间接性正相关.子能力间相互依赖关系如图4所示.

高阶思维能力与毕业要求指标点的对应关系如表4所示.

表4 高阶思维能力与毕业要求指标点的对应关系

结合团队合作机制这一可观察量，以团队协作能力为例.智能车竞赛由一个团队共同运作，通过组内成员相互评估考核其他成员的高阶思维能力，在一个智能车竞赛组中，成员所做的贡献固然有异，不同贡献的人考核时得分应当不同，如何进行合理的打分并使团队所有队员都能竭尽全力工作，已然成为一种困境，为了解决这种困境，采用博弈论纳什均衡来解决同组成员评分问题.

一个智能车竞赛小组由n位学生组成，i=1,2,…,n,代表同一小组的学生.每个学生的效用水平与个人的努力关联，ui表示第i个人的效益水平,n维向量u=(u1,…,uI,…,un)为n位学生的效用水平组合[16]；Eui为期望效用，即学生效用水平的期望值,与战略发生的概率和效益水平有关；学生参加智能车竞赛根据实际情况选择多种战略，若n位学生每人选择一个战略，n维向量s=(s1,…,si,…,sn)称为一个战略组合，其中si是小组中第i位学生选择的战略[13]；最优战略均衡是所有学生的最优战略的组合，记为s*=(s1*,…,si*,…,sn*)[16].用si*表示第i位学生在均衡情况下的最优战略，它是i学生所有可能战略中使ui或Eui最大化的战略[5].一般来说，ui是所有参与人的战略组合函数，i学生的最优战略通常依赖于其他人的战略选择；除i以外其他所有人的战略组合由向量s-i=(s1,…,si-1,si+1,…,sn)表示，si*是给定s-i情况下第i位学生的最优战略，即

ui(si*,s-i)≥u(si′,s-i),∀si′≠si*.

(6)

对所有i=1，2，…，n，上式成立.

设n个参与者的战略式表述博弈G={S1,…,Sn;u1,…,un},战略组合s*=(s1*,…,si*,…,sn*)是一个纳什均衡，如果对于每一个i，si*是给定其他参与人选择s-i*=(s1*,…,si-1*,si+1*,…,sn*)的情况下第i个参与人的最优战略，即

ui(si*,s-i*)≥ui(si′,s-i*)，∀si∈Si，

(7)

或者，si为下式最大化时的解：

si*∈arg maxui(s1*,…,si-1*,si,si+1*,…,sn*),i=1,2,…,n.

(8)

若一个竞赛团队由三人组成，参加智能车竞赛时，每个人有“工作”和“偷懒”两种战略.智能车竞赛小组评分机制组员间形成一个G={工作,偷懒;u1,u2,u3}的博弈，该评分博弈存在占优战略均衡.团队共同得分取决于平均努力程度，即专家意见，第i(i=1,2,3)个人的效益水平ui为小组得分减去个人努力的成本，效益水平用数值表示，数值大小与效益水平(收益)成正比，团队A提交的团队合作机制如表5所示.

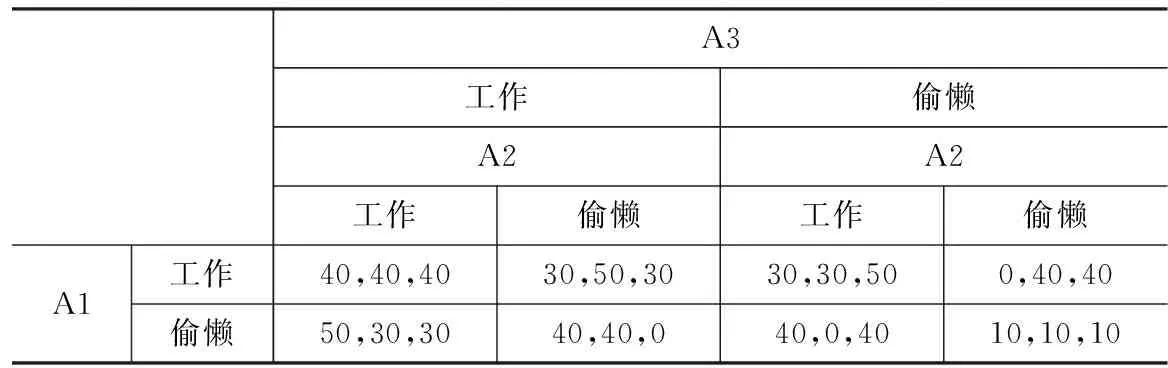
表5 学生两难困境

该博弈论存在一个占优战略均衡，满足：

ui(si*,s-i*)≥ui(si′,s-i*)，∀si∈Si， ∀i.

(9)

例如，当A1选择偷懒时，G={S1,…,Sn;u1,…,un}={{偷懒*，工作，工作；50*,30,30},{偷懒*，偷懒，工作；40*,40,0},{偷懒*，工作，偷懒；40*,0,40},{偷懒*，偷懒，偷懒；10*,10,10}},无论其他成员选择何种战略，A1的效益水平最高，“偷懒”都是最优战略.

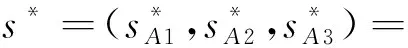
为了解决两难困境，团队B提出一种新的评分机制，根据对团队的贡献大小为学生评级，排名第一加30分，第二加20分，第三不加分，每个学生为团队其他两位成员评级，如表6所示.

表6 团队评级情况

若有两个队员等级相同，则让第三个队员对这两个队员重新评级.如表6所示，B1为第一，B2第二，B3第三.修改表5博弈，如表7所示.

表7 带有奖励机制的队员处境

如表7所示，此时“工作”成为占优战略，博弈称为合作占优博弈.B1选择“工作”战略，G={S1,…,Sn;u1,…,un}={{工作*，工作，工作；83*,83,83},{工作*，偷懒，工作；75*,50,75},{工作*，工作，偷懒；75*,75,50},{工作*，偷懒，偷懒；50*,30,30}},如图6所示，团队合作机制趋于positive，团队协作能力相对较强.

每个队员给同队成员打分(不包括自己)，再利用如下公式计算最终成绩.

个人最终成绩=小组成绩*组内人数*r/100，

(10)

式中：r是互评系数，互评系数是对团队成员的打分，即博弈论法评分得分.评价应尽量客观，包括工作量，工作难度，团队贡献等的综合评价，分数越高，贡献越大.经过归一化处理后，得到互评系数，互评系数之和为100，小组平均成绩由指导老师决定.例如，经过上述博弈论评分机制，GB1={工作;90}，GB2={工作;90}，GB3={工作；90}，为3位同学的战略和效用水平，小组成员“工作”成绩85分，则3位同学的最终成绩为

B1：85*3*37.5/100=95.6,

B2：85*3*34.4/100=87.7,

B3：85*3*28.1/100=71.7.

把博弈论用在组内互评上的优势：

(1) 从同队组员那里获得评分依据.

(2) 没有给队员伪造信息提升自己分数的机会.

(3) 消除工作两难的困境.

4 仿真实验

4.1 先验与条件概率计算

某高校2016-2017年全国大学生“恩智浦”杯智能汽车竞赛比赛结果如表8所示.

表8 某高校2016-2017年“恩智浦”杯智能车竞赛比赛结果

将“国家级”“华南赛区和省一等奖”“省二、三等奖”“未获奖”依次设定为优秀、良好、中等、不及格四个等级，则首节点的先验概率值如表9所示.在本认知诊断模型中，未获奖不代表考核不及格，只是先验概率的一种设定方法.

表9 首节点的先验概率

由于篇幅有限，现以父节点“路径识别”和子节点“传感器知识”之间的条件概率设置为例，其他节点间的条件概率同理可得.如表10所示，当传感器知识认知能力为优秀级别时，与获得优秀级别的路径识别关联度较高(专家一般给出5、6)，而与获得不及格级别的路径识别能力检测关联度不高(专家一般给出2、3).

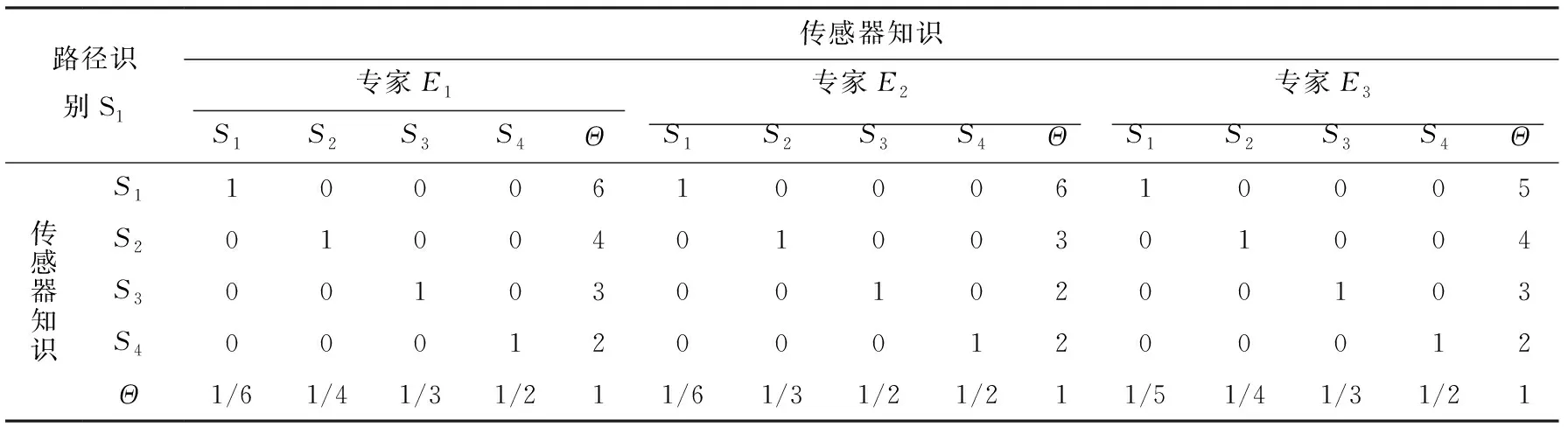
表10 专家Ek在路径识别S1(优秀)下传感器知识的相关度矩阵

注：S1代表优秀，S2代表良好，S3代表中等，S4代表不及格.

根据知识矩阵求出专家E1,E2,E3的基本概率分布如表11所示.

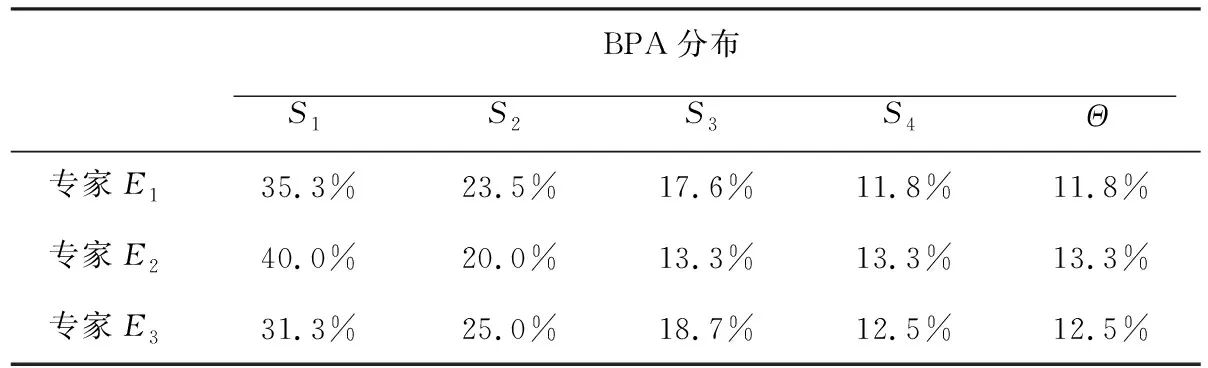
表11 专家E1,E2,E3的BPA分布

对三位专家的基本概率分布取值进行排序，依次得出专家给出的最小值、最可能值、最大值，最后使用泊松分布(Pert)对多个专家进行意见综合.

4.2 Pert分布仿真

利用Pert分布来模拟专家意见，通过AHP分析得出：S1优秀、S2良好、S3中等、S4不及格四个等级的条件概率，对三个专家的意见进行排序，得出最低概率，最可能概率，最高概率.在@RISK软件中调用函数Risk Discrete，得到如图7所示的Pert分布，从而对三位专家意见进行拟合，结果如表12所示.

表12 专家E1,E2,E3综合BPA分布

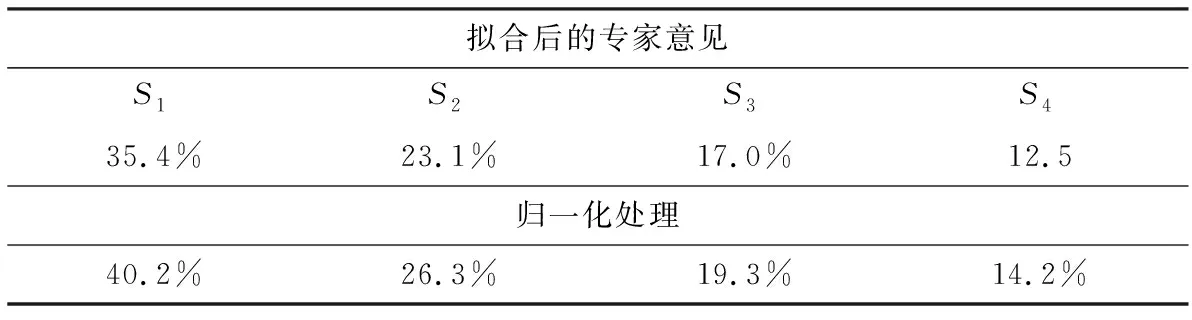
拟合后的专家意见S1S2S3S435.4%23.1%17.0%12.5归一化处理40.2%26.3%19.3%14.2%

4.3 贝叶斯网络仿真

学生参加智能车竞赛,在路径识别环节知识的掌握程度和能力的强弱以及毕业要求能力指标点达成度如图8所示.各项可观察量趋于优秀时，相关的知识和能力值也因可观察量的改变趋于优秀.但仿真结果仍然不是很理想，例如没有设定相关阈值评价学生的各项达成度，该认知诊断模型的结构与参数需要进一步精炼，这些将在后续工作中改进.

5 总结

本文以12条毕业要求能力指标点为依据，基于贝叶斯网络，并以产出为导向，构建了以证据为中心的智能车竞赛路径识别认知诊断模型.依据智能车竞赛的内容和规则，提出一种确定贝叶斯网络的结构和参数的方法.基于博弈论设计了团队合作能力的证据辨识规则，避免了成员伪造信息提高自己评级的机会.最后对该认知诊断模型进行仿真，得到学生参加智能车竞赛路径识别模块包括知识和能力的整体熟练度.