习知识，炼方法，善反思——新课程背景下一道解析几何课堂教学的实践与思考

☉浙江省慈溪中学 张 军

解析几何是在平面直角坐标系的框架下用代数的方法来研究图形的几何性质，问题一般涉及的变量多，运算量大，综合性强，是公认的“一根难啃的硬骨头”.它是高中数学的难点，但却是高考的热点.学生学习解析几何主要存在以下问题：

1.学生平时学习时只停留在“听懂”“看懂”层面，未能真正理解，缺少进一步深入研究；

2.运算能力薄弱，不能合理转化；

3.缺少题后反思，很少有知识联系.

那么如何在课堂教学中破解出现的问题，是值得每位教师思考的问题.本文作者结合教学实践和思考，运用重过程、重应用、重体验、重参与的课堂模式，以学生为主体，充分暴露解题思维和探究过程，引导学生提出问题、分析问题、解决问题，破解学生对解析几何的“恐惧”.

一、试题呈现

在平面直角坐标系xOy中，点B与点A（-1，1）关于原点O对称，P是动点，且直线AP与BP的斜率之积等于

（1）求动点P的轨迹方程.

（2）设直线AP和BP分别与直线x=3交于点M、N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由.

此题涉及椭圆的标准方程及简单几何性质、直线方程、直线与椭圆相交弦长的计算、三角形面积的计算等.背景简单、条件熟悉，起点低，入口宽，突出主干知识，紧扣考试说明.但是学生在第（2）问碰到很大困难，究其原因，主要是解题方法选择不当，运算能力不强，缺少知识的融会贯通和灵活应用.

二、教学片段

师：请同学们迅速做一下第（1）问.

生1：因为点B与点A（-1，1）关于原点对称，所以可得点B的坐标为（1，-1），

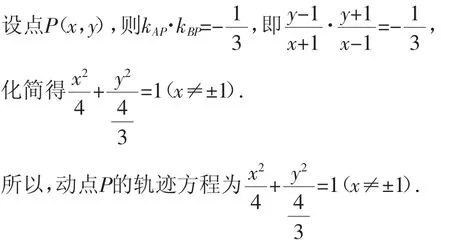
师：同学们，第（1）问很简单，但计算一定要仔细准确，因为一旦错误，那整个大题都错了，同时还要注意由于两条直线斜率的存在，所以x不能取±1.

师：下面请同学们考虑一下第（2）问怎么处理.

生2：对于存在性问题可先假设存在，目标是求出△PAB和△PMN的面积.

师：那么你说说该如何求这两个三角形的面积呢？

生2：先要求出这两个三角形的一条边长及其所对应的高.

师：那么如何求解呢？

生2：先选择参数，由于要求点P的坐标，所以选择斜率k为参数，这样可得到直线AP和BP，然后利用韦达定理即可求出点P的坐标.

设直线AP的方程为y=k（x+1）+1，则直线BP的方程为

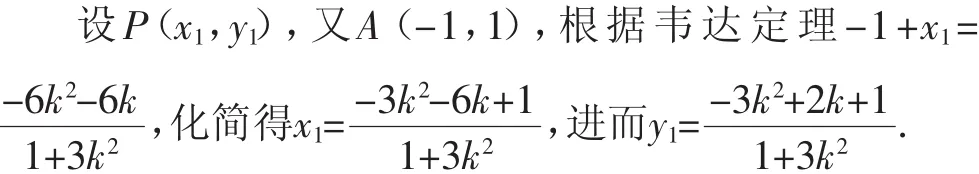
师：很好！有了点P坐标，接下来我们要做什么工作呢？

生3：接着求P到直线AB和x=3的距离，即两个三角形的高，再求得线段AB和MN的长，就可以表示出三角形的面积.

师：非常棒！请大家一起共同来尝试下.

教师巡视，查看学生的解题过程，但是这个思路很快就遇到了困难，选择一份做不下去的草稿投影在黑板上：

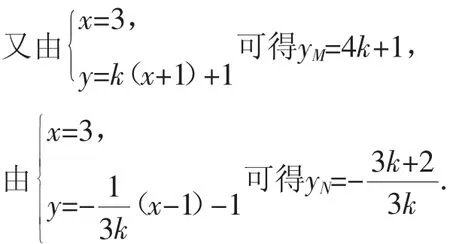
若存在点P，使S△PAB=S△PMN，则P必在直线AB的右上方，且yN>yM.

因为1+3k2≠0，所以12k2+9k+1=0.

但接下去点P的横坐标x1求不出来了，想用求根公式求出k的值然后代入x1=，又觉得运算量太大，几乎不可能完成，不知所措了.

师：生2的思路是不是不能做了呢？是否必须要把k解出来？

生4：不必求出k的值，这里设而不求的思想，得到

教室里传来了同学们的惊叹之声，佩服生4的高超运算智慧，变繁为简，化腐朽为神奇.

师：对于生2的方法容易想到，但却不容易解出答案，运算有些复杂，所以平时我们一定要加强运算能力训练，只要运算中有一点点失误，就很难得到正确答案.那么还有其他思路吗？

生5：根据三角形的面积公式可得

师：太棒了！生5能将所学知识灵活应用，融会贯通，运算量明显比上一种思路要简洁，值得我们大家学习.

生6迫不及待地站了起来：我对生5的思路还有另外一种处理方式：

如图1，连接|BM|、|AN|，

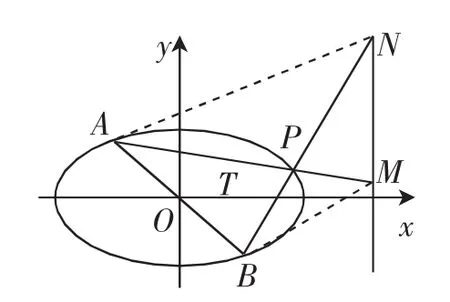
图1

师：生6的方法也很妙.

师：解析几何一般处理方式是几何问题代数化，其实质就是将问题中的几何要素用坐标或方程表示，利用坐标运算和方程思想，来研究几何图形的性质.但仍然要注意图形的性质，用图形的几何性质，有助于简化计算.数形结合思想是解析几何的精髓所在.

师：通过这节课你有什么体会？大家可以相互交流，并应用到以后的学习中去.

生7：要加强基本运算能力的训练，加强方法的比较，通过分析与比较有时会得到“巧算”.

师：是的，在学习解析几何时，要重视基本思路、基本运算；要重视分析、比较；要重视过程步骤、答题规范.

三、拓展延伸

讲授完该题，学生对如何啃下解析几何这根“硬骨头”有了初步认识，教师从该题出发，进行适当改编，进一步培养学生分析问题的能力和提升学生的解题能力.

（2）椭圆C上是否存在三点D，E，G，使得S△ODE=S△ODG=？若存在，判断△DEG的性状；若不存在，请说明理由.

四、课后反思

1.进行解析几何教学时要重通法，教算理，帮助学生掌握解题策略

对于解析几何的教学，并不是题目讲得越多越好，也不是技巧讲得越巧妙越好，而是要“授人以鱼，不如授人以渔”.要坚持以学生为主体，多角度示范解题分析，强化数形结合的运用，重视数学思想和方法来指导解题，避免盲目地生搬硬套.如通过第（2）问的讲解，点拨学生总结解决解析几何问题的方法步骤，利用设而不求的方法、转化相关条件、注重整体代换等运算技能，从能力角度提高对运算的认识，反思运算方法的优化，不断提高运算水平.同时解题方法的多样性，有助于拓展学生的思维.

2.进行解析几何教学时要以探究为径，发挥学生主体作用

俗话说“百闻不如一练”，只有让学生“动起来”，才能使所学知识“活起来”“用起来”.所以要让学生学会思考，学会探究，学会研究数学问题.教师做好引导，以问题模式为驱动，在时间和空间上保证学生学习活动正常展开和学习行为真实发生，要让学生亲身经历学习过程，引领学生思考，在形式和本质上保证学生大脑处于积极的思维状态，培养学生探究思考的好习惯.

3.进行解析几何教学时要创设问题情景，培养学生抗挫能力

大多数学生对解析几何题有着一种恐惧感，在探索思路、分析求解的过程中经常会出现“绞尽脑汁而无从下手”“运算繁杂而中途作废”的思维受阻现象.所以解决解析几何问题，信心很重要，坚持也很重要.但信心和坚持需要我们从平时的教学和学习中去获取，在平时的教学中鼓励学生去做这类题目，在他们算不对，化简不出的时候个别辅导，与学生一起运算，让他们在心理上先接受这类题，相信这是他们能解决的问题.在解析几何这条路上，享受的不是结果，而是在失败中找出成功的途径，培养耐心，磨砺心志，这就是解析几何带给我们的最美之处.