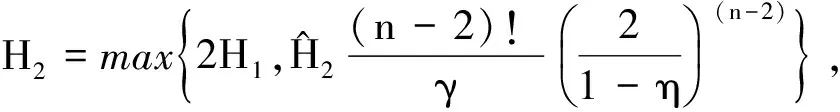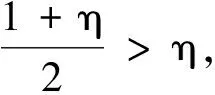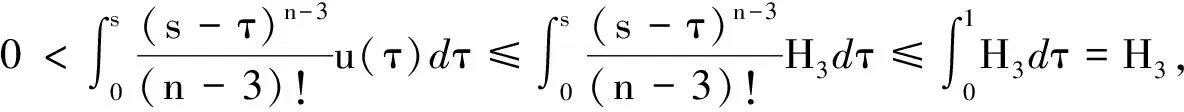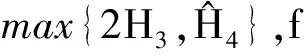一类n阶常微分方程边值问题正解的存在性

刘 颖,陈逸藻,李 琳(.沈阳航空航天大学 理学院，沈阳 036;.辽宁大学 数学院，沈阳 0036)

1999年马如云[1]研究了三点边值问题

正解的存在性，此后上述结果被推广到了更广泛的边界条件及更一般的微分方程情形。目前所能见到的推广结果多数是三、四阶微分方程[2-14]。这里通过降阶法和格林函数法将微分方程边值问题转化为微分积分方程边值问题。通过适当选取积分下限克服了不等式证明过程中的困难，利用范数形式的锥拉伸和锥压缩不动点定理，将上述边值问题推广到了更一般的n阶微分方程情形，得到了解的存在性结果。

1 主要结论

记

定义:当f0=0且f=时，称f为超线性函数；当f0=且f=0时，称f为次线性函数。

比如，f(v)=vβ，β为常数且β>1时在[0,+)上为超线性函数；f(v)=vβ，β为常数且0<β<1时在[0,+)上为次线性函数。

下面始终假设α,η为常数，且0<η<1,0<αη<1。

定理

(A)f(v)∈c([0,+),[0,+))

(B)a(t)∈c([0,1],[0,+))，且存在使得a(x0)>0

(C)f0=0且f=

(D)f0=且f=0

假设条件(A),(B)成立，则当f(v)满足(C)或(D)时，下面边值问题(1)至少有一个正解。

(1)

2 问题转换

设v(n-2)(t)=u(t)，利用常数变易法及v(0)=v′(0)=…=v(n-3)(0)=0，可将v(t)表

u(τ)dτ[15]，则原边值问题化为二阶微分积分方程边值问题,如式(2)所示。

(2)

再通过格林函数法可将上述边值问题转化为积分方程问题,如式(3)所示。

(3)

3 重要引理

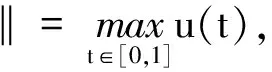
(4)

引理1[1]若u(t)是(4)的解，则对任意的t∈[0,1]，都有u(t)≥0

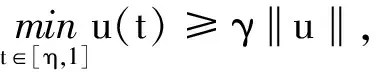
设u(t)∈c[0,1]，且u(t)≥0，定义算子A为

(5)

引理3 记

K={u(t)|u(t)∈c[0,1],u(t)≥0,

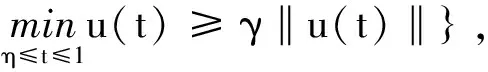
易证K是一个锥[2]，另外由算子的定义不难验证

再由引理1和引理2知AK⊆K,下面证明A是全连续算子。

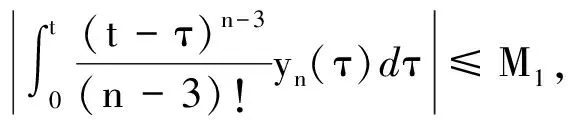
所以{Ayn}一致有界。

显然{Ayn}等度连续，由Ascoli-Arzela定理知{Ayn}存在收敛子列，即A是紧算子。

设yn,y0∈K且yn→y0(n→)，则

即A是连续算子，综上A是全连续算子。

4 定理证明

定理1 设条件(A),(B),(C)成立，则边值问题(1)至少有一个正解。

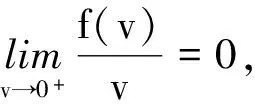
(6)

因此取Ω1={u(t)|u(t)∈c[0,1],‖u(t)‖

即

当u(t)∈K∩∂Ω1，有‖Au‖≤‖u‖

(7)

又由条件(A),(C)，f=+，即，所以对任意ρ>0，存在使当时,有即f(v)>ρv。在这里取ρ满足

(8)

设

(9)

所以

(10)

(11)

即

当u(t)∈K∩∂Ω2时，‖Au‖≥‖u‖

(12)

定理2 设条件(A),(B),(D)成立，则边值问题(1)至少有一个正解。

证明：由条件(A),(D)，f0=+，即，由无穷大定义，对任意ω>0，存在H3>0,使0ωv。在这里取ω满足

取Ω3={u(t)|u(t)∈c[0,1],‖u(t)‖

即当u(t)∈K∩∂Ω3，有‖Au‖≥‖u‖

由条件(D)，f=0，即由极限定义对任意λ>0，存在使时,有<λ，即f(v)<λv。在这里取λ满足

(13)

以下分两种情况讨论：

情形1：f(v)有界，即存在N>0使得对所有v∈[0,+)，有f(v)≤N，选取

并取

Ω4={u(t)|u(t)∈c[0,1],‖u(t)‖

则当u(t)∈K∩∂Ω4时，有u(t)≥0，且‖u(t)‖=H4

即

当u(t)∈K∩∂Ω4时，‖Au‖≤‖u‖

则由(13)式

即

当u(t)∈K∩∂Ω4时，‖Au‖≤‖u‖

综上，定理得证。

[1] 马如云.非线性常微分方程非局部问题[M].北京：科学出版社，2004.

[2] 郭大钧.非线性泛函分析[M].济南：山东科学技术出版社，1985.

[3] 杨春风.一类非线性四阶问题正解的存在性和多解性[J].数学进展，2014，43(1)：133-144.

[4] 高芳,江卫华.一类分数阶微分方程边值问题的三个正解[J].数学的实践与认识，2014，44(1)：273-278.

[5] BAI Z.On positive solution of a nonlocai fractional boundary value problem[J].Nonlinear Anal，2010,72:916-924.

[6] 谢春杰.带非齐次边界条件的二阶常微分方程边值问题正解的存在性[J].烟台大学学报,2012,25(4):251-255.

[7] 余立.一类四阶两点边值问题正解的存在性与多解性[J].理论数学,2013,3(6):347-353.

[8] 王宏洲,葛渭高.奇性边值问题的正解存在性[J].数学学报,1999,42(1):111-118.

[9] 赵增勤.非线性奇异微分方程边值问题的正解[J].数学学报,2000,43(1):179-118.

[10]毛安民.正指数超线性Emden-Fowler方程奇异边值问题的正解[J].数学学报,2000,43(4):623-632.

[11]姚庆六.一类特殊非线性Neumann边值问题正解[J].重庆大学学报(自然科学版),2007,30(9):93-95.

[12]彭海军,高强.非线性齐次常微分方程两端边值问题精细积分法[J].大连理工大学学报,2010,50(4):477-480.

[13]李耀红.一类分数阶微分方程组积分边值问题的正解[J].高校应用数学学报,2015,30(1):109-116.

[14]汪卫华,杨彩霞.一类多点共振方程组边值问题正解的存在性[J].河北科技大学学报,2016,37(4):340-348.

[15]刘颖.n阶非线性常微分方程两点及三点边值问题解的存在性的进一步结果[J].应用数学学报，2003，26(1)：72-90.