一种带变异算子的粒子群算法

(朔州师范高等专科学校 数学与计算机系,山西 朔州 036000)

通过观察和模拟鸟类觅食行为,我们得到了粒子群算法(PSO),这是一种通过随机搜索找到最优解的算法.由于算法简单易行,因此被普遍应用于神经网络和函数优化领域.

PSO算法也存在缺点,如收敛慢,容易困于局部收敛.因此,本文提出一种基于变异算子的粒子群算法(MPSO),该算法根据一定概率改变运行过程中发现的当前个体极值，从而跳出局部收敛,然后执行全局搜索.通过性能函数测试,新算法能有效进行全局寻优,且提高收敛进度和解的精确度.

1 标准粒子群优化算法(PSO)

该PSO算法需要开始设置一组随机粒子.也就是说,在D维空间中随机设置m个粒子,其中粒子k的位置表示为xk=(xk1,xk2,…,xkD),k=1,2,…,m,粒子k的行进速度是vk=(vk1,vk2,…,vkD),到目前为止,粒子k找到的最佳位置为pbk=(pbk1,pbk2,…,pbkD),整个粒子种群所找到的全局最佳位置为gb=(gb1,gb2,…,gbd),每个粒子的速度和位置的计算如下:

(1)

(2)

其中,k=1,2,…,m是粒子数,i=1,2,…,n是运行次数,d=1,2,…,D是维数;c1和c2是加速常数,它们代表粒子运动到gb和pb位置的权重;vkd∈[vmin,vmax],vmin和vmax是常数,根据问题具体设定;r1和r2是介于[0,1]之间的随机数;w是惯性系数,通常在0.1～0.9之间,如果算法运行时w线性减小,该算法的收敛性能将更优越[1],因此本文算法w采用以下形式:

(3)

(其中当前运行次数是i,算法运行总的次数是imax;最小惯性系数是wmin,最大惯性系数是wmax).

2 带变异算子的粒子群算法

文献[2]提出了一种速度变动PSO算法,该算法是改变粒子速度以跳出局部最优.本文效仿该思想,提出在合适的时机按一定几率修改粒子的个体极值pbk的粒子群算法(MPSO),从而粒子的行进方向得以变动.通过这种方式,粒子可以在其它区域中搜索最佳值,跳出局部最优值,并改善全局收敛.

然而,当执行变异操作时,通常难以控制,因此必须首先确定变动的时机.这个时机与粒子群的行进状况有关,粒子群的行进状况可以通过种群适应度的方差来给出.

有m个粒子,favg——这群粒子当前的平均速度,fk——第k粒子适应度,σ2——粒子群的种群适应度方差,则:

(4)

其中f为归一化定标因子,f的值是:f=max{1,max{|fk-favg|}},k=1,2,…，m.

[注]:群体适应方差σ2的大小可反映粒子群的“收敛”程度.σ2较小粒子群接近收敛(全局收敛或者局部收敛); 相反,粒子群是非收敛的并且需要随机搜索.因此,如果σ2值很小并且问题的理论最优值差算法所产生的实际最优值很远,我们认为该算法已经局部收敛.

若算法困于局部收敛,则让粒子k的个体极值pbk根据概率p变异.

若算法困于局部收敛,则让粒子k的个体极值pbk根据概率p变异.

(5)

fm(理论最佳值),f(gb)(gb适应度),μ(收敛精确度),γ值通常远小于σ2的最大值.

粒子k的个体极值pbk作如下变动:

① 首先生成一个与正态分布N(0,1)匹配的随机数r.

②pbk变异:pbk=pbk×(1+r)

具体算法流程图1所示.

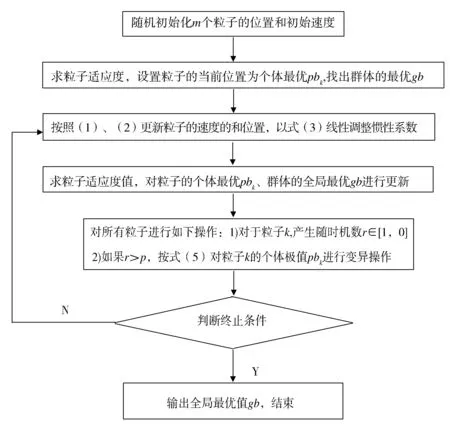
图1 算法流程图

3 实验

由三个性能测试函数Griewank函数、Rosenbrock函数、Ackley函数(求最小值)来验证本文MPSO算法的性能,同时与标准PSO算法、文献[2]的算法作仿真分析和比较.三个性能测试函数[2]如下:

Griewank函数

(6)

Rosenbrock函数

(7)

Ackley函数

(8)

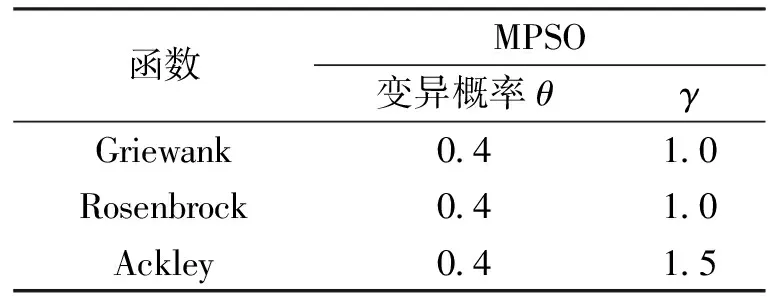
表1 实验参数

上述三个性能测试函数是多峰值函数,具有大量局部极点,最小值为零.实验的参数见表1,其中:算法的种群大小都设置为50,收敛精确度μ=10-7,c1=c2=2,最大运行次数设定为1 000,惯性系数w:

其中i为当前的运行次数,imax为总运行次数,wmin为最小惯性系数,wmax为最大惯性系数,惯性系数w从0.9线性递减到0.1.表2出示了运行20次后得的结果.

表2 三种算法的仿真结果

为了更好地反映三种算法的收敛性能,如图2、图3、图4所示.为了比较,纵坐标是适应度的对数.

图2 Griewank函数，xk =[-50,50],D=30最佳适应度进化曲线

图3 Resenbrock函数xk =[-50,50],D=30最佳适应度进化曲线

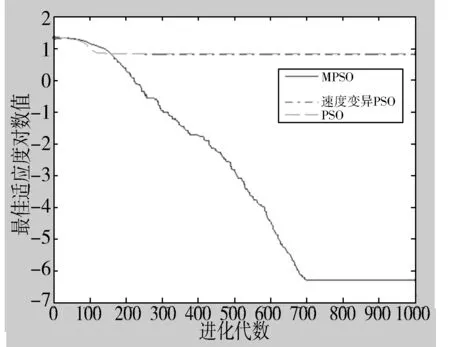
图4 Ackley函xk∈[-50,50],D=30最佳适应度进化曲线

从表2的数据和图2、图3、图4可以发现,MPSO算法较PSO算法和文献[2]的算法更接近最优解,全局收敛性能、收敛进度和精确度更好.

4 结论

为了更好的找到全局最优解,文中效仿文献[3]的算法,在标准PSO算法的基础上,做了改进,得到了具有变异算子的粒子群算法(MPSO).验证结果显示,该算法的改进方案是可行的,得到的结果更接近最佳值,全局收敛性能更好.