基于主成分分析和梯度重构的全波形反演
史才旺 何兵寿*
(①中国海洋大学,山东青岛 266100; ②青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266071; ③海底科学与探测技术教育部重点实验室,山东青岛 266100)
1 引言
全波形反演(FWI)利用了地震记录中的振幅、相位等信息,是一种分辨率较高的速度建模方法。Tarantola[1]最早提出了FWI的基本方法,该方法基于广义最小二乘反演理论,利用理论波场与反传播的残差波场的互相关构造梯度方向。此后,FWI方法得到不断完善,Bunks等[2]首先提出了时间域多尺度反演的理念,从低频逐步反演到高频,显著降低了FWI的非线性性。Pratt[3]首先提出了频率域的FWI思想,其优势在于仅利用几个离散的频率就能对模型实现高精度重建。此外,Shin等[4]的Laplace域反演和Sirgue等[5]的混合域反演方法进一步丰富了FWI理论。
FWI技术在过去的30年间取得了长足的进步,现在已经开始应用于实际资料。FWI本身是一套完美的数学体系,然而在实际应用中,由于地震记录总是会受到不同程度的破坏,如低频能量的缺失、各种噪声的影响等,FWI 很难取得理想的效果。实际地震记录包含各种随机噪声和相干噪声,在噪声较强时,能量较弱的反射同相轴甚至可能被完全掩盖。在模拟记录中不含噪声,而由残差记录计算出的梯度会包含噪声,因此适当的去噪处理对FWI十分必要。不同的相干噪声有不同的针对性压制方法。对于随机噪声,常规的策略是对信号进行滤波处理,以牺牲部分有效信号予以去除。对于频带与有效信号重合的噪声,则一般通过有效信号之间的相关性予以压制,如SVD方法[6,7]、小波变换[8]和近年兴起的Curvelet变换[9,10]等。若将这些方法直接作用于地震记录,当信噪比较低时对波形伤害很大,会导致FWI数据的不匹配。
对于含噪地震数据,目前一般使用几种特殊的目标函数改善反演效果。常规FWI基于L2范数,其实用性较强,但抗噪能力较弱。Tarantola[11]和Hugues等[12]的实验和实际资料处理结果表明,L1范数对噪声并不敏感。Huber范数和混合范数都是L1范数与L2范数的结合,由于其带有L1范数的特性,因而抗噪性较强,但是这两种范数都需要指定具体阈值用于切换L1/L2范数,若阈值不合适可能导致反演效果较差[13,14]。Brossier等[15]的弹性波实验结果也表明,L1范数比L2范数抗噪性强,对存在明显异常值的地震记录也能得到更好的反演结果。但是L1范数本身也具有一定缺陷,如当数据误差接近于零时,基于L1范数求取的目标函数梯度会出现不稳定,而L2范数则没有这个问题。当地震记录中噪声严重时,L1范数也难以得到正确的结果。此外,成景旺等[16]使用了基于柯西分布的目标函数,其对数据异常、线性噪声具有良好的压制能力。
目前,大多数基于L1范数的目标函数对数据异常及一些相干噪声压制效果良好,但对随机噪声压制能力有限[17],前人在L2范数框架下提出了多种改进方法。Brossier等[18]指出,在进行含随机噪声的频率域反演时,通过增加频率个数可以在一定程度上改善反演效果。Oh等[19]在单尺度、全频域弹性波反演时构建了一个降噪函数,针对不同频率估算信噪比,以增大高信噪比频段在梯度中的占比。这种方法需要针对实际情况指定一个合适的降噪因子;此外,该方法只适合单尺度反演,当高频段信噪比较低时,会降低反演分辨率。Kwon等[20]利用平面波编码方式提高编码记录的信噪比,改善了含噪弹性波记录的反演效果。
为进一步降低随机噪声对反演结果的影响,本文结合主成分分析,通过对梯度进行额外处理,实现了一种抗噪性更强的L2范数FWI方法。模型实验表明,该方法在信噪比较低时仍能得到正确的反演结果。
2 FWI基本理论
频率域声波方程可以视为一个关于波场值U的方程组
AU=S
(1)
式中:A为阻抗矩阵;U为由所有网格点波场值组成的列向量;S为震源列向量。
在最小二乘意义下,FWI的目标函数为
(2)
式中:E为目标函数;m为待反演参数,文中m代表速度;Ns为炮数; δdi为第i炮各检波点残差,它是模拟地震记录与实际观测地震记录之差,i为炮点序号; *代表取共轭。由此推导出目标函数关于速度参数的梯度

(3)
为加快误差函数的收敛速度,本文利用L-BFGS法对梯度方向进行优化[21],随后通过抛物线拟合法求取一个合理的步长,从而实现模型更新。
3 随机噪声对FWI的影响
为了详细说明随机噪声对FWI的影响,使用Marmousi 2模型进行含噪数据单频反演实验。首先对Marmousi 2部分模型(图1a)采用1000m×1000m的高斯滤波器进行平滑(默认海水层速度为1500m/s),得到初始模型(图1b)。对Marmousi 2部分模型及初始模型(图1)进行正演得到频率域2.0Hz地震记录的实部(图2),对其进行2.0Hz的单频FWI,得到2.0Hz单频FWI结果(图3),采用以拟Hessian矩阵[22]对角元素为初始矩阵的L-BFGS法对梯度进行了优化。由FWI反演结果可见,含噪数据反演结果(图3b)与不含噪数据反演结果(图3a)存在较大差距,且前者的迭代次数更多。
FWI追求的是地震记录的误差最小,但并不能识别数据中的噪声,而噪声与地质模型无关,因此噪声的存在可能导致模型误差不断扩大。图4为2.0Hz单频FWI相对误差曲线。由图可见,其变化趋势为先减小后增大。这是因为在反演初期,初始模型与真实模型相差较大,导致地震记录差距明显,因而残
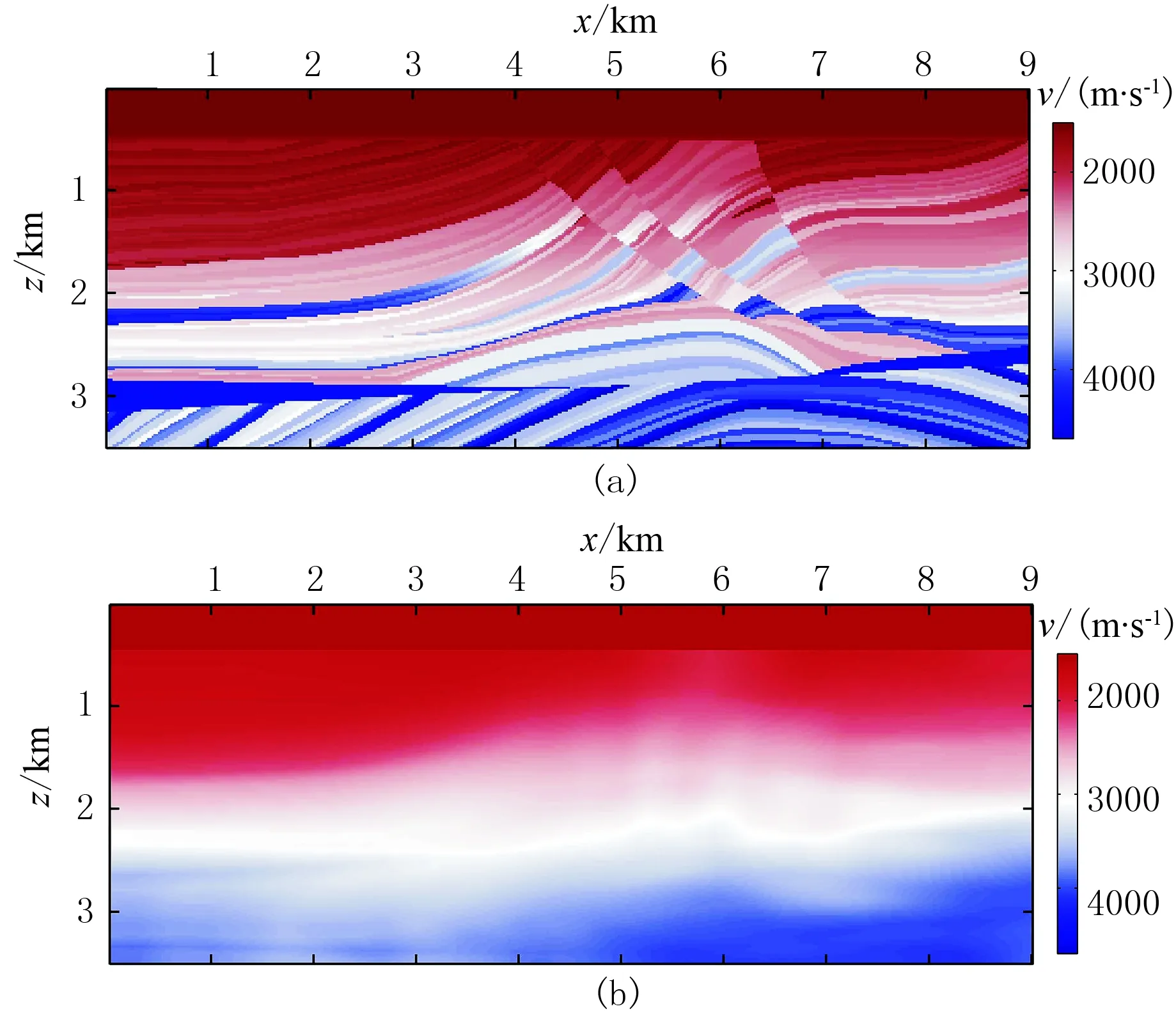
图1 Marmousi 2部分模型(a)及初始模型(b)
模型网格数为175×450,网格间距为20m。震源为主频8Hz的雷克子波,原始记录共有112炮数据,炮点深度为20m,炮间距为80m,共有450道接收,检波器均匀分布于模型表面
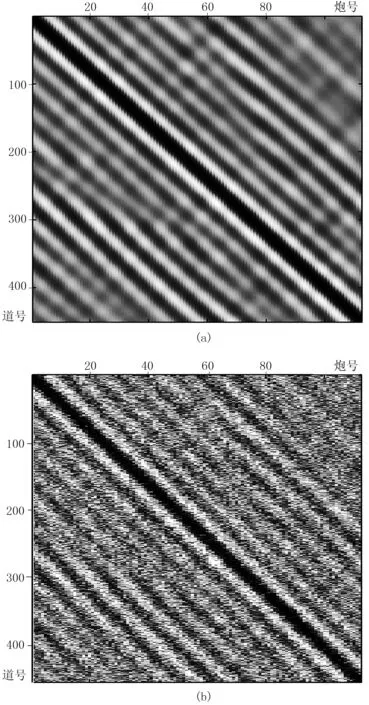
图2 频率域2.0Hz地震记录的实部 (a)不含噪声; (b)含高斯白噪声(信噪比为1)
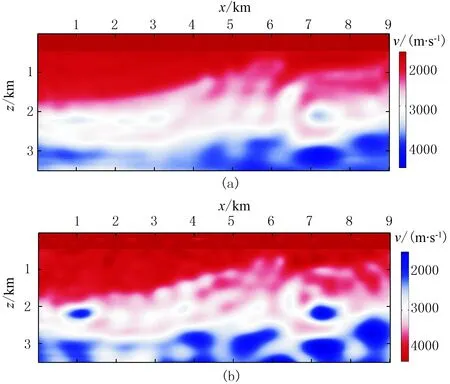
图3 2.0Hz单频FWI结果 (a)不含噪声; (b)含高斯白噪声
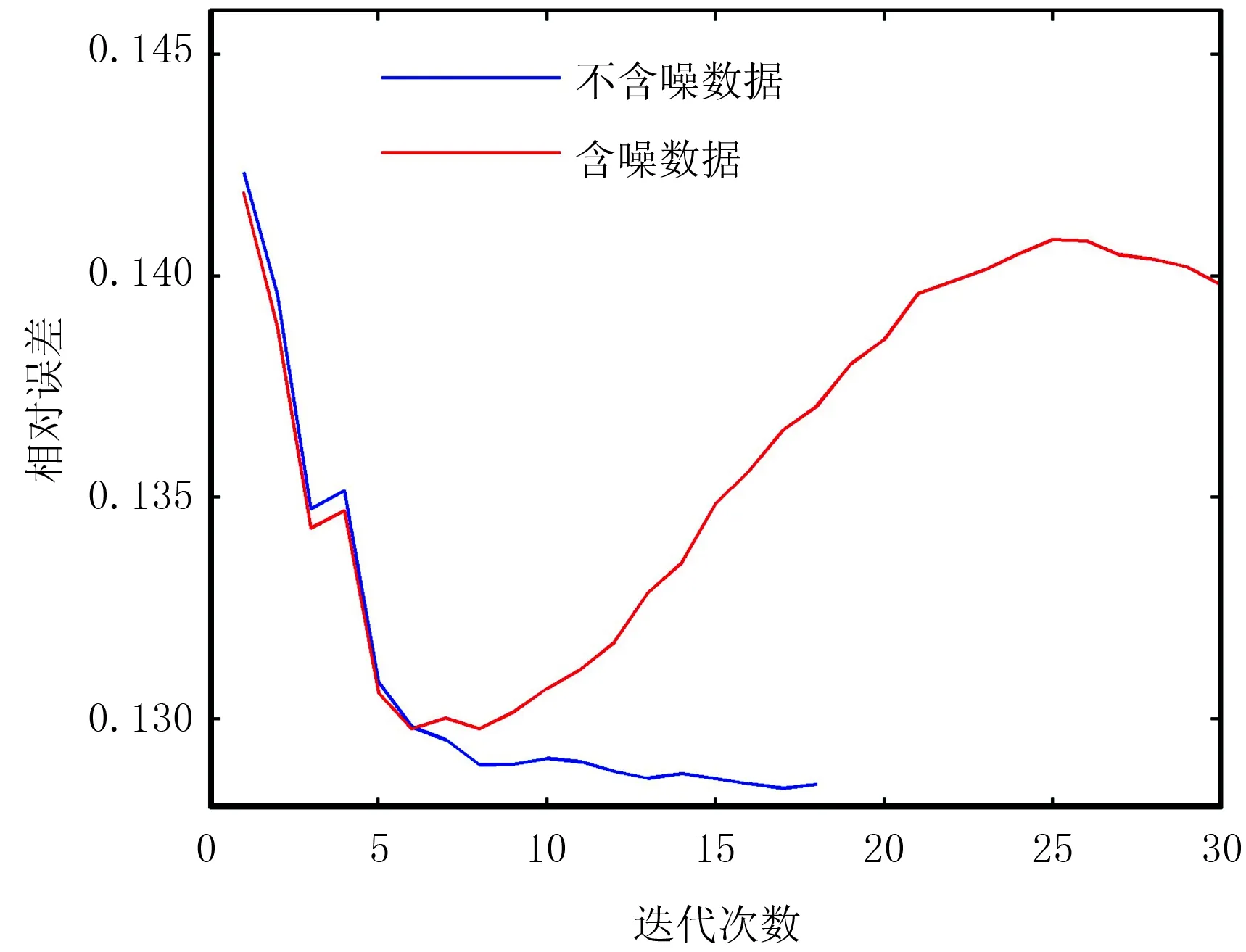
图4 2.0Hz单频FWI相对误差曲线 模型误差errm根据标准模型mstd、FWI结果mFWI 按errm=计算[23]
差记录中有效信号能量强,噪声能量弱,使反演中的梯度较准确。当反演继续进行,反演模型与真实模型较接近时,残差中有效信号能量弱,噪声能量占主导,此时梯度受噪声破坏严重,导致模型朝着错误方向更新。若能在模型误差发散前及时使反演过程收敛,则反演结果的可靠性将大为提高。
基于以上分析,本文引入一种新的梯度处理方式——主成分分析(PCA),在反演中能达到以下目的:①在信噪比较高时能获得准确的梯度,不影响其收敛速度;②在信噪比较低时对梯度进行优化,在提取有效信息的同时阻止模型朝着错误方向更新。
4 基于PCA的梯度重构
PCA是一种多元统计分析方法,其目的是使用少数几个特征变量描述一组具有相关性的多个变量,这些特征变量互不相关,为原始的多个变量的线性组合[24]。PCA最初是一种降维方法,Liu等[25]利用这种方法对地震资料进行压缩从而大大降低了FWI的计算量; 段超然等[26]在此基础上利用PCA实现了高效的波场重构反演,为常规FWI提供了可靠的初始模型。在图像处理方面,PCA也是一种良好的去噪方法,在电磁数据去噪中也有较多应用[27,28]。
在常规FWI中,总梯度是由单炮梯度直接叠加得到的。在本文中,每一炮的梯度都被视为描述总梯度的一个变量,而总梯度是所有炮的梯度的一种线性组合。假设某次反演迭代获取了N炮的梯度信息,每一炮梯度含有M个空间点的速度梯度。首先将每一炮的梯度拉伸为一个列优先存放的列向量,并将这些列向量组合为一个M×N阶的矩阵A,称为设计矩阵。矩阵A的第i(i=1,2,…,N)列代表第i炮记录得到的所有空间点的梯度;第j(j=1,2,…,M)行代表第j个空间点每一炮对应的梯度值。对A进行PCA,返回三个矩阵变量,分别为主成分系数矩阵P、主成分变量矩阵A′及其对应的特征值矩阵λ,其中A′的每一列称为一个主成分,它们满足
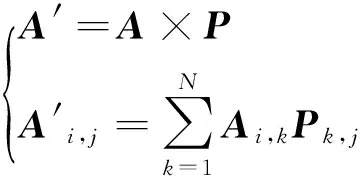
i=1,2,…,M;j=1,2,…,N
(4)
特征值矩阵λ描述了每一个主成分对矩阵A的贡献值,λ由大到小排列,值越大则此主成分越重要,其对应的主成分排位也越靠前。上式表示的过程可以改写为
A=A′×P-1
(5)
即原始梯度可以通过主成分和主成分系数进行重构。由于A的主要信息集中于特征值较大的前几个主成分中,因而只要选取几个重要的主成分进行重构就可以还原矩阵A的大部分信息,其他主成分则可以舍弃,该过程可记为
(6)
式中:B′也为M×N阶矩阵,它是由A′中只保留前k个主成分得到的;B为重构得到的新梯度,将B按行进行叠加便可得到最终的梯度场。
地震记录中的噪声会通过波场的互相关运算映射到梯度中,当噪声具有随机性时,可认为各炮梯度中包含的噪声也互不相关,与此同时,各炮的有效梯度则具有很强的相关性。当有效梯度能量总体占优时,主成分重构能得到高信噪比的梯度信息。随着反演的进行,有效梯度能量减弱,常规FWI得到的梯度中噪声能量占主导,依据此梯度更新得到的新模型则会引入大量噪声,导致模型误差扩散。在各炮噪声不相关的情况下,各主成分贡献值差距不大。由于只选取了少量主成分参与重构,此时重构的梯度与原始梯度相差较大,可以使目标函数不降低或者极缓慢地降低。这种特性可以使反演过程快速收敛,不会引起误差扩散。
主成分重构需要选定使用的主成分个数,Kaiser准则是一种常用的选取主成分个数的经验方法。Kaiser准则建议只保留特征值大于1的主成分,其他主成分则舍弃。本文即采用这种方法,不过应用Kaiser准则需要先对设计矩阵A进行标准化,将其每一列转换为均值为0、方差为1的标准化向量,而重构得到的梯度也要去除标准化影响。事实上,由于FWI需要不断迭代,因此其对主成分个数没有较高要求,直接利用第一主成分进行反演依然能得到正确结果,只是其收敛速度逊于Kaiser准则方法(附录A)。
5 模型实验
在频率域反演中,噪声的影响与自身强度和频谱分布都有关,因而有必要选取不同强度、不同性质的随机噪声分别进行实验。在加入白噪声的情形下,由于白噪声的能量在频谱上均匀分布,低频段受噪声影响严重,震源主频处信噪比较高。因此,在反演含白噪声的地震数据时,往往低频段的反演效果很差,直接导致高频段反演失败。为更好地突出文中方法的优势,文中又利用频谱能量分布不均衡的高斯有色噪声进行了实验。
5.1 含高斯白噪声的FWI
使用Marmousi 2部分模型及初始模型(图1)进行实验,观测系统保持不变。在频率域采用单频连续反演策略,频率点由低到高依次为2.0、2.5、3.75、5.625、8.125、11.25Hz,频率迭代的终止条件是前后两次迭代的反演结果相对误差小于0.001。频率选择是频率域FWI反演精度的重要影响因素,频率选取越密集、频率越高,反演精度越高。就本文的实际情况而言,11.25Hz的反演结果已经接近原模型。对于不含噪声的情况,常规FWI给出了准确的反演结果(图5)。
5.1.1 常规FWI
为说明本文方法应用于不同信噪比地震数据时的反演效果,分别在原始记录中加入不同强度的高斯白噪声。图6、图7分别为信噪比为1.0、0.5时不同频率点原始记录傅里叶变换的实部,用以说明各频率的信噪比。利用常规FWI对上述地震记录进行反演,图8为常规FWI在5.625Hz频点的第一次迭代获取的梯度,可见梯度形态或多或少都偏离了真实模型。由常规FWI对含高斯白噪声地震数据的反演结果(图9)可见:由于信噪比的影响,反演效果不理想,其中浅层反演较为准确,深层受噪声破坏严重。如精确模型的最大速度为4700m/s,反演结果则分别达到了5580、6685m/s,严重偏离了真实值,导致反演结果误差较大。
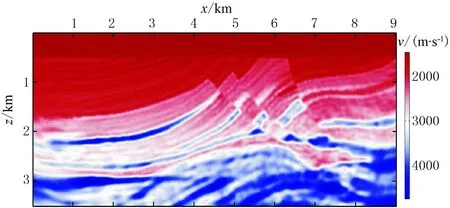
图5 不含噪声地震数据的FWI结果

图7 信噪比为0.5时不同频率点的原始记录傅里叶变换的实部 (a)2.0Hz; (b)3.75Hz; (c)11.25Hz
5.1.2 基于单炮的主成分梯度重构FWI
首先,将每一炮的梯度单独转换为设计矩阵A的一列,直接利用主成分梯度重构方法进行反演。此时A是一个78750×112阶的矩阵,矩阵标准化后利用Kaiser准则选取特征值大于1的主成分参与重构。
图10为基于单炮的主成分梯度重构FWI在5.625Hz频点的第一次迭代获取的梯度,与常规FWI在5.625Hz频点的第一次迭代获取的梯度(图8)进行对比可知,前者的精度更高。图11为基于单炮的主成分梯度重构FWI对含高斯白噪声地震数据的反演结果,与常规FWI对含高斯白噪声地震数据的反演结果(图9)相比,前者更加贴合真实模型。图12为基于单炮的主成分梯度重构FWI的2.0Hz单频反演相对误差曲线。由图可见,基于单炮的主成分梯度重构FWI的反演过程稳健,即使在信噪比最低的第一个频点,反演也没有出现误差扩散现象,具体表现为:当信噪比为1.0时,反演结果几乎完全还原了精确模型的特征(图12a);当信噪比为0.5时,模型浅层得到了较好的还原,深层虽然稍差,但是也基本体现了精确模型的轮廓,并且最大速度约为5000m/s,速度误差在合理范围内(图12b)。
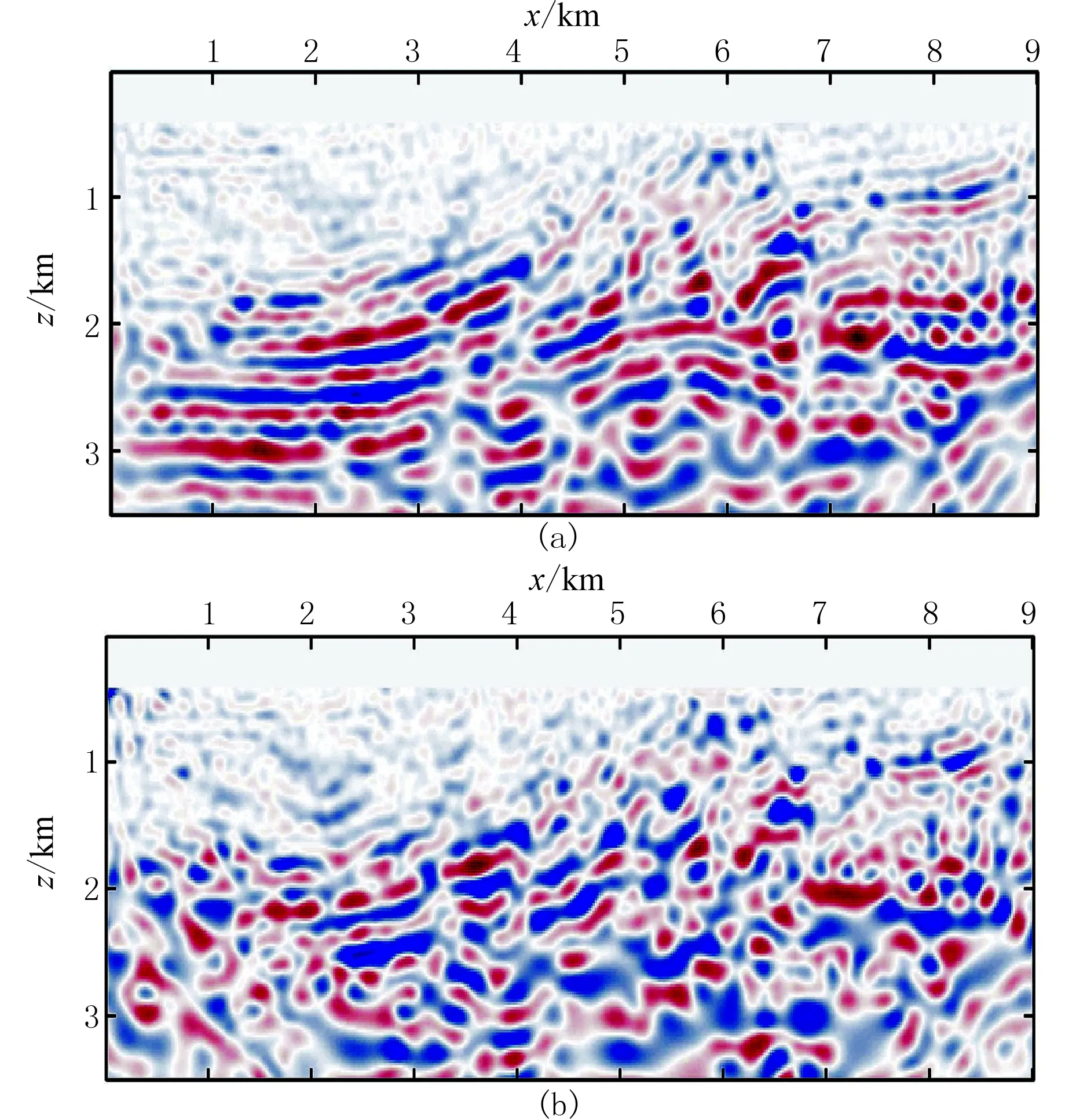
图8 常规FWI在5.625Hz频点的第一次迭代获取的梯度 (a)信噪比为1.0; (b)信噪比为0.5
5.1.3 基于组合炮的主成分梯度重构FWI
在本文方法的理论假设中,每一炮的梯度被视为对总梯度的一个描述。在主成分分析和重构中,这些梯度组成了一个训练集,在理想情况下该训练集中的梯度应当都是由某个公共部分加上随机噪声组成。实际上每一炮的梯度只反映了炮点附近的梯度信息,频率较高时这一点尤为明显,这必定会对梯度重构产生一定影响。为此,本文提出了基于组合炮的主成分梯度重构方法。顾名思义,这种方法首先将所有炮梯度分成L个组,每个组内的梯度先累加得到一个组合梯度,将其变形为设计矩阵A的一列,之后在再对A进行主成分分析和重构。由于主要目的是使训练集的公共成分尽量相似,所以本文采用等间隔采样的方法进行炮分组(图13),尽量使每个组合里的炮点能够均匀地覆盖整个模型。这里将所有炮点按照空间位置均匀分成10个组,并对10个组合梯度进行主成分分析和重构。
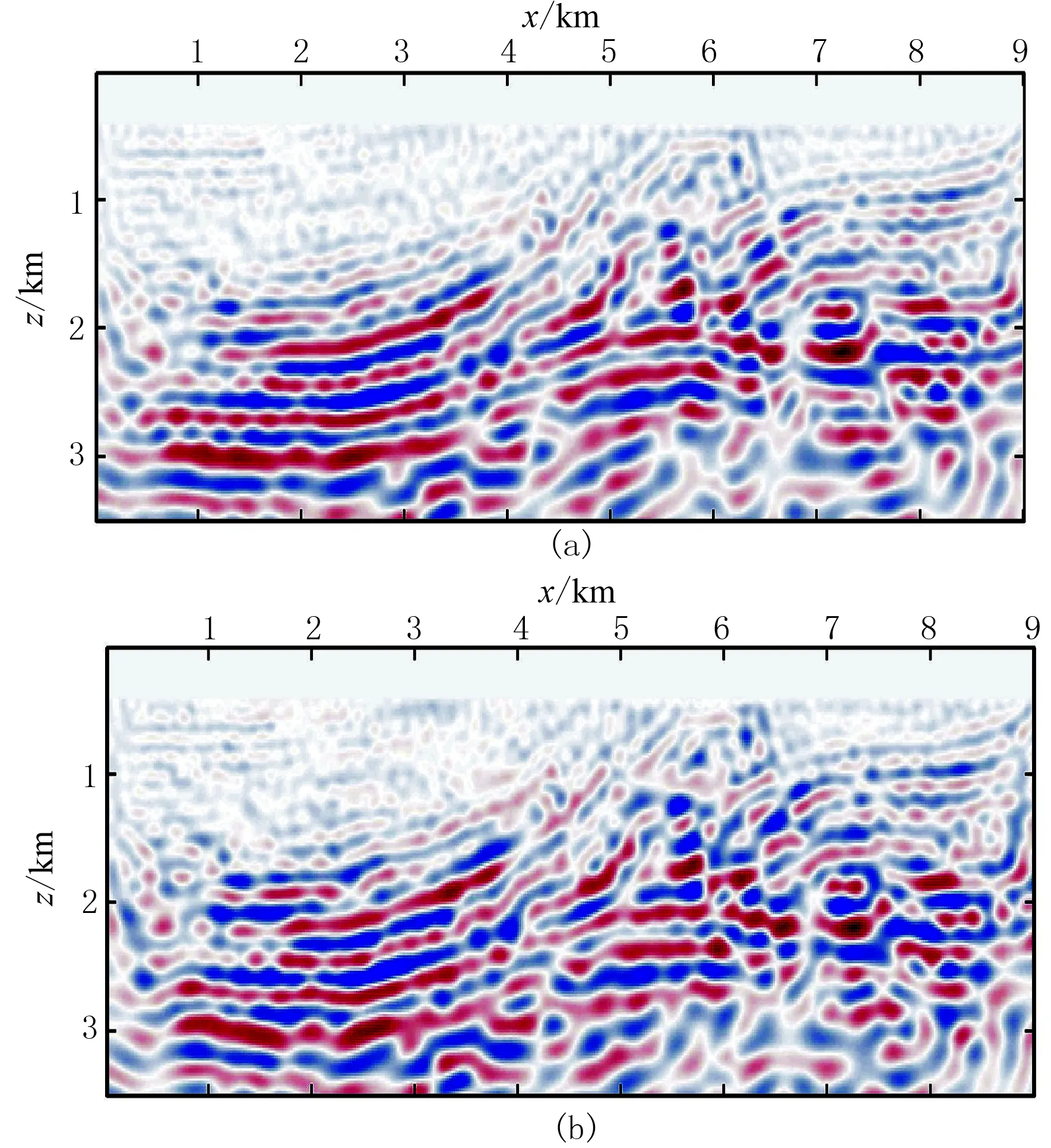
图10 基于单炮的主成分梯度重构FWI在5.625Hz 频点的第一次迭代获取的梯度 (a)信噪比为1.0; (b)信噪比为0.5
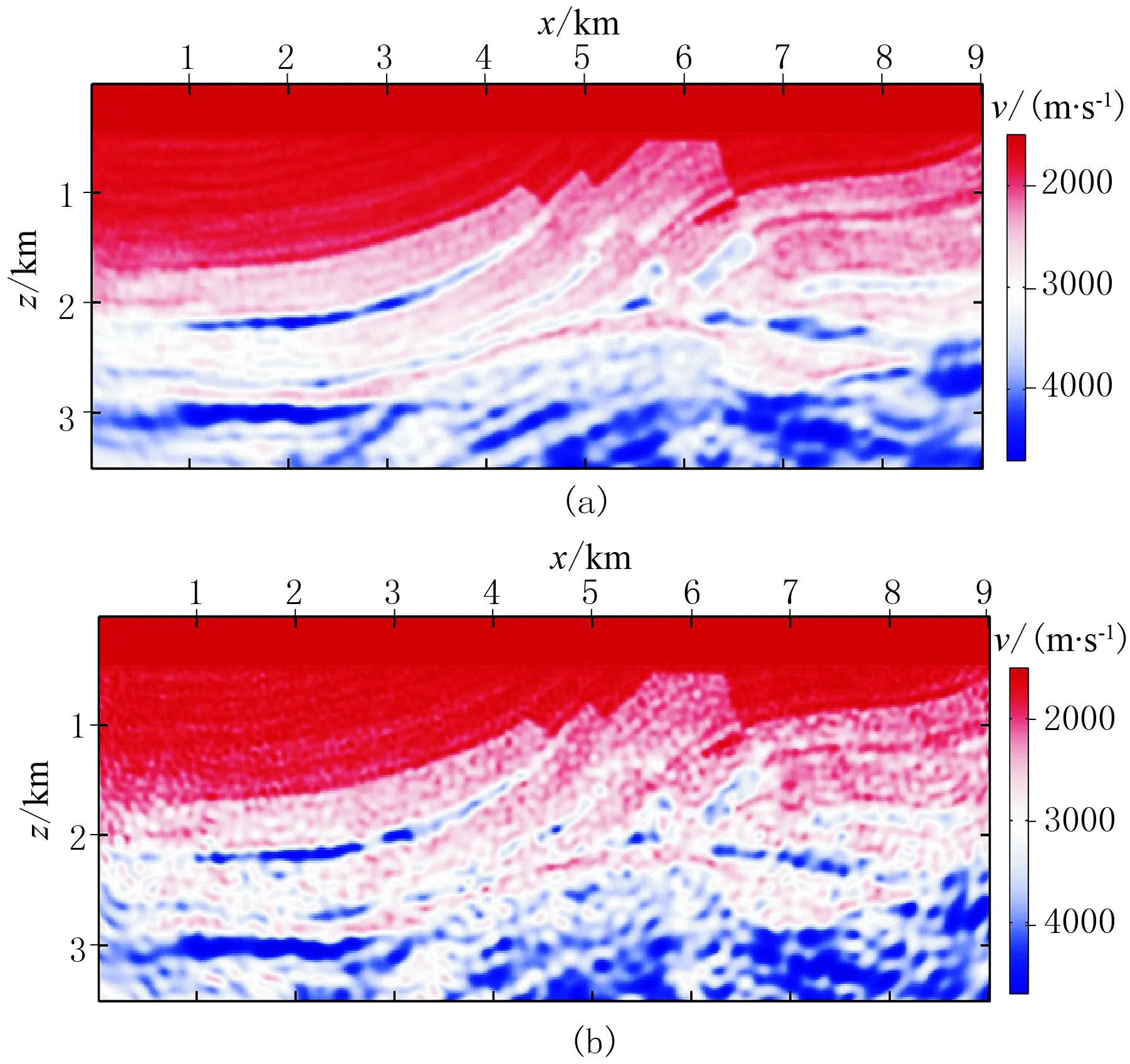
图11 基于单炮的主成分梯度重构FWI对含高斯白噪声 地震数据的反演结果 (a)信噪比为1.0; (b)信噪比为0.5
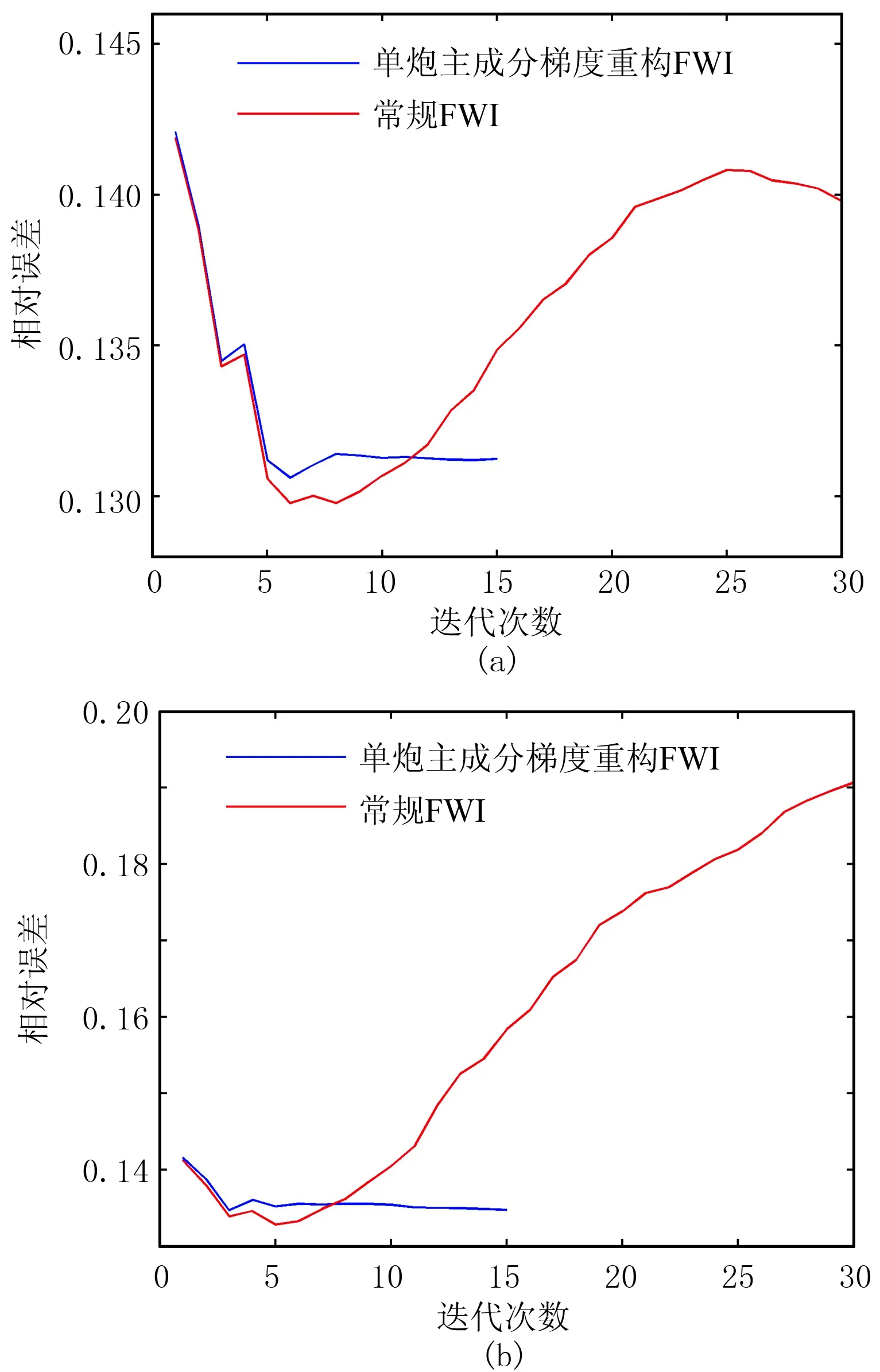
图12 基于单炮的主成分梯度重构FWI的2.0Hz 单频反演相对误差曲线 (a)信噪比为1.0; (b)信噪比为0.5
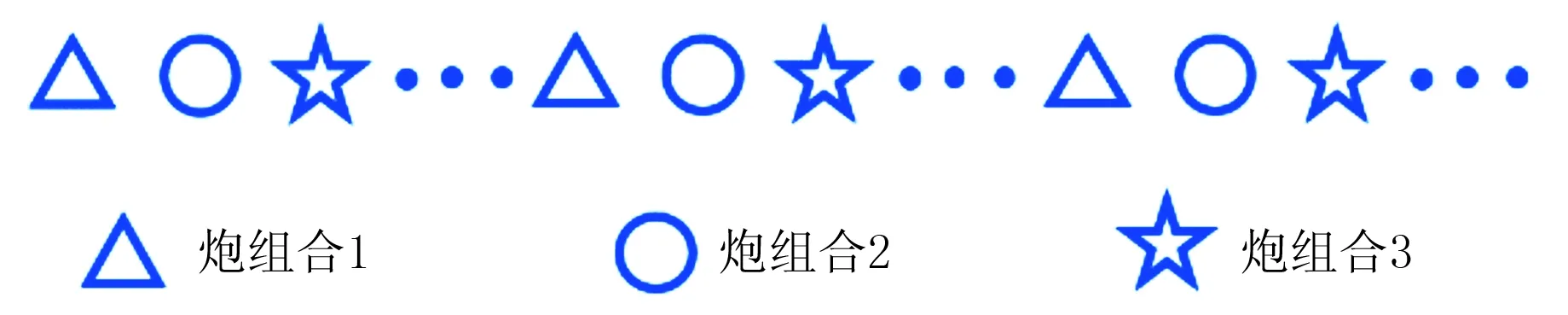
图13 炮分组方法示意
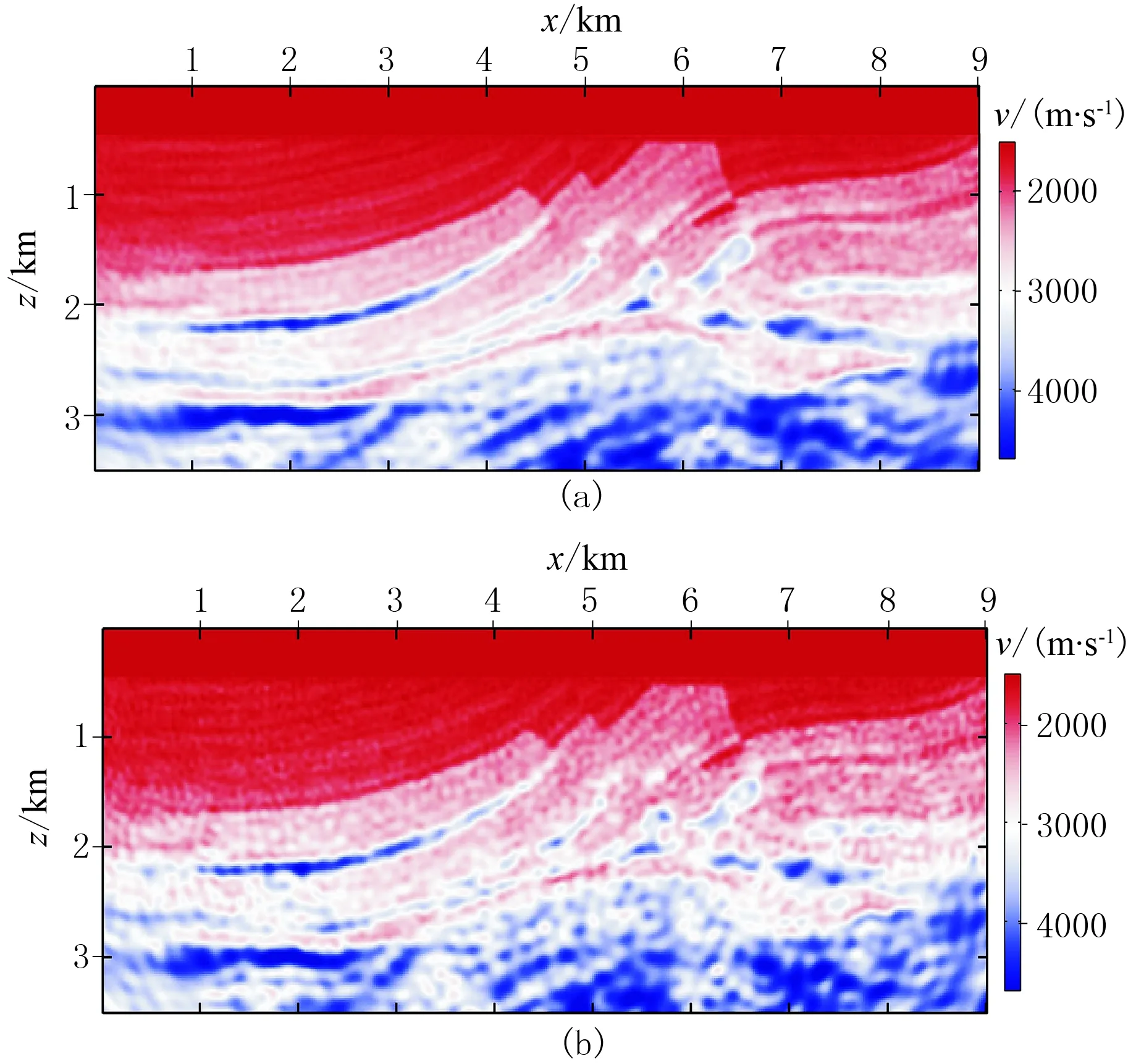
图14 基于组合炮的主成分梯度重构FWI对 含高斯白噪声地震数据的反演结果 (a)信噪比为1.0; (b)信噪比为0.5
利用此方法再进行反演实验,其他参数不变,得到基于组合炮的主成分梯度重构FWI对含高斯白噪声地震数据的反演结果(图14)及其2.0Hz时的模型相对误差曲线(图15)。表1为含高斯白噪声时不同方法的反演精度对比,可见改进后的FWI方法得到的结果更加接近真实模型。
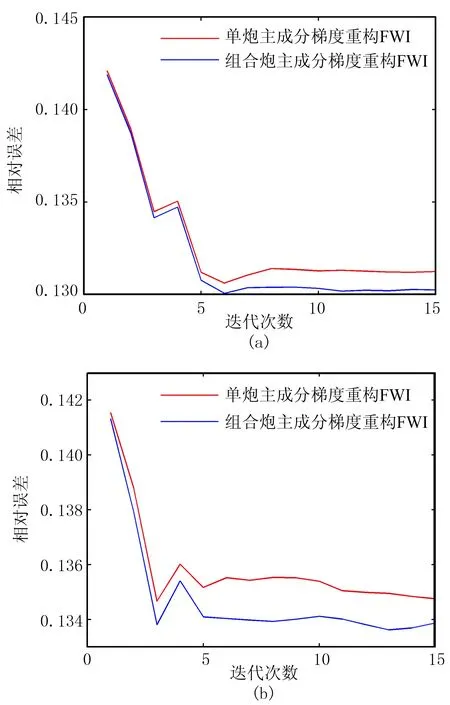
图15 基于组合炮的主成分梯度重构FWI的 2.0Hz单频反演相对误差曲线 (a)信噪比为1.0; (b) 信噪比为0.5表1 含高斯白噪声时不同方法的反演精度对比
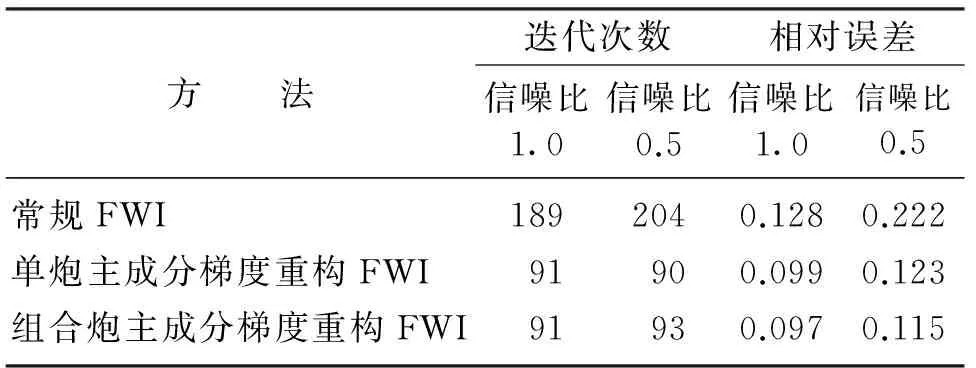
方 法迭代次数相对误差信噪比1.0信噪比0.5信噪比1.0信噪比0.5常规FWI1892040.1280.222单炮主成分梯度重构FWI91900.0990.123组合炮主成分梯度重构FWI91930.0970.115
5.2 含高斯有色噪声的FWI
频率域FWI从低频开始逐步提高频率,低频段的反演结果对高频段影响严重。为进一步说明主成分梯度重构方法对多尺度反演的普适性,本文在地震记录中引入有色噪声。有色噪声的能量随频率变化,实验中加入的有色噪声能量的频率分布与地震记录一致,即任意频率的信号能量和噪声能量都满足
(7)
式中:Sf为频率f处的单频信号能量;Nf为单频噪声能量。
利用常规FWI和基于组合炮的主成分梯度重构FWI进行反演,得到含高斯有色噪声地震数据反演结果(图16)。表2为含有色噪声时不同方法的反演相对误差对比。可见:组合炮主成分梯度重构FWI的反演相对误差明显小于常规FWI;对于常规FWI,由于信噪比较高,低频段的反演结果相对准确,但是后续频段的误差累积依然使反演结果的相对误差较大。
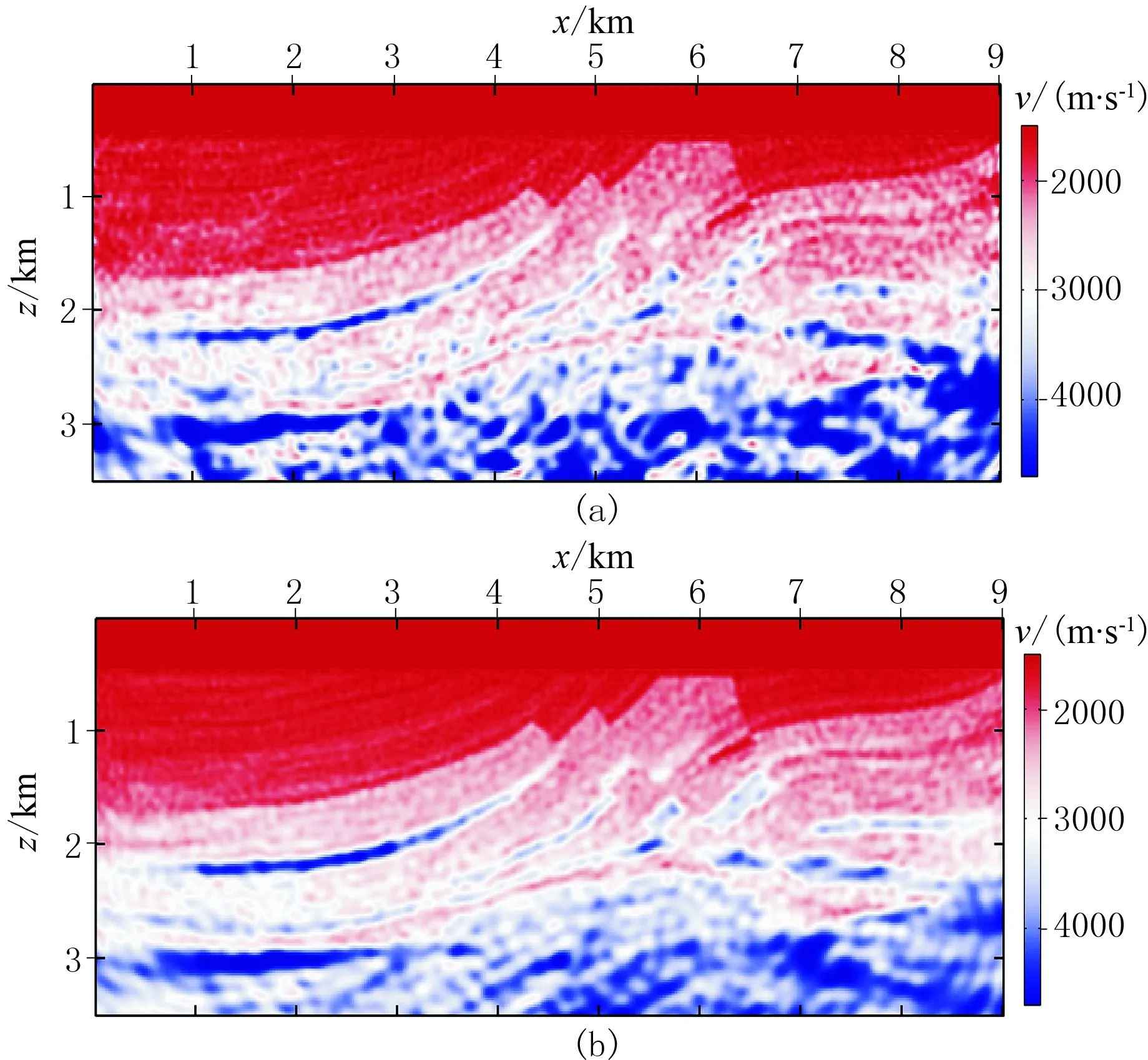
图16 含高斯有色噪声地震数据反演结果 (a)常规FWI; (b)基于组合炮的主成分梯度重构FWI表2 含有色噪声时不同方法的反演相对误差对比

频率/Hz2.02.52.755.6258.12511.25常规FWI0.1360.1270.1240.1270.1280.137组合炮主成分梯度重构FWI0.1300.1250.1160.1090.1060.105
5.3 计算量对比
主成分分析和重构过程的运算量都很小,基本不会使反演过程变慢。同时,由于常规FWI的误差函数常常无法收敛(图4),因此迭代次数会达到预设的最大值,从而造成常规FWI的耗时很长且效果差。表3列出了基于组合炮的主成分梯度重构FWI与常规FWI的计算量,表中所有实验基于同一平台,所用的CPU型号为Intel Core i5-4460,主频为3.20GHz,内存为8G,利用UMFPACK软件包提供的LU分解法进行频率域正演。由表3可见:在含白噪声的数据反演中,改进FWI的运算时间不到常规FWI的一半;在含有色噪声的数据反演中,运算时间也大幅减少。
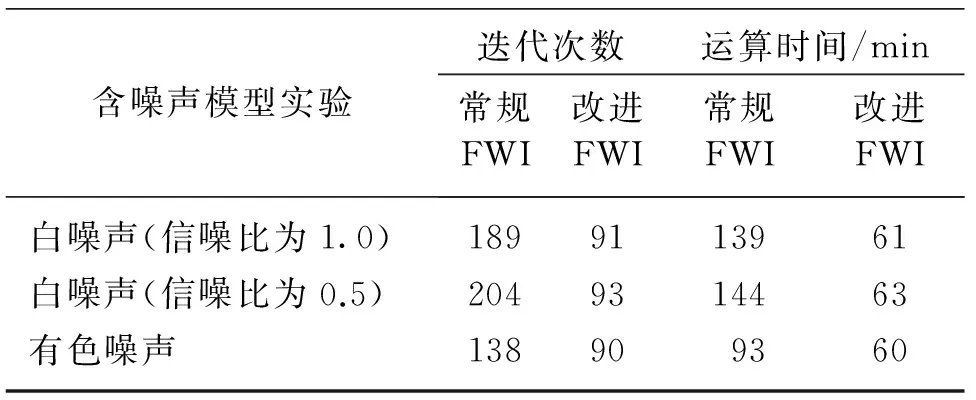
表3 基于组合炮的主成分梯度重构FWI 与常规FWI的计算量
综上所述,当地震记录中含有噪声时,主成分梯度重构FWI较常规FWI的抗噪性更强,模型误差收敛速度也较快,计算量更小。此外,基于组合炮的梯度重构FWI比基于单炮的梯度重构FWI的效果更好,反演的相对误差更小。
6 结束语
随机噪声会对FWI的梯度产生破坏,甚至导致反演失败。在研究随机噪声对FWI影响的基础上,本文引入了基于PCA的FWI方法。利用PCA将各炮梯度重新组合为一组不相关的主成分,选取部分主成分重构梯度以压制噪声的扩散,此方法在低信噪比情况下实现了FWI。
模型实验表明,基于PCA和梯度重构的FWI方法具有较高的抗噪性。此外,本文对比了基于单炮和组合炮的主成分梯度重构FWI方法,结果表明后者的效果更佳。
尚需指出,本文所添加的噪声均服从高斯分布,且所用的经典的PCA的鲁棒性仍然不足,有关其他类型的噪声对波形反演的影响及其压制策略、引入改进的高鲁棒性PCA进一步提高对噪声和数据异常的适应性等问题是今后的研究方向。
附录A 只选取第一主成分进行梯度重构的反演效果
本文中使用Kaiser准则的目的是选定特定数量的主成分参与重构,这是一种经验做法。一般可以认为特征值大于1的主成分中有效信号居多,反之则噪声能量占优。考虑到FWI的过程需要不断迭代,因此,即使某次重构的梯度缺失了部分有效信息,在之后的迭代中也可以得到弥补,但相应的反演过程的收敛速度可能会受到影响。针对文中所述的基于单炮的主成分梯度重构FWI,为与之对比,在其他各参数不变的情况下,仅利用第一主成分进行梯度重构。
图A1为含高斯白噪声地震数据的反演结果,图A2为含高斯白噪声地震数据的反演相对误差曲线。由图可见,应用Kaiser准则的梯度重构方法的反演结果更为精确。表A1为含高斯白噪声地震数据的反演相对误差对比。由表A1可见,Kaiser准则方法最终模型的相对误差达到0.099,只利用第一主成分的相对误差为0.101。在收敛速度方面,应用Kaiser准则的梯度重构方法显然更快。值得注意的是,Kaiser准则的作用与参与PCA 的梯度数量有关,即梯度数量越多,两种方法差距越明显。而当使用基于组合炮的主成分梯度重构方法时,Kaiser准则本身选取的主成分数量就较少,因而两种方法差距并不大。
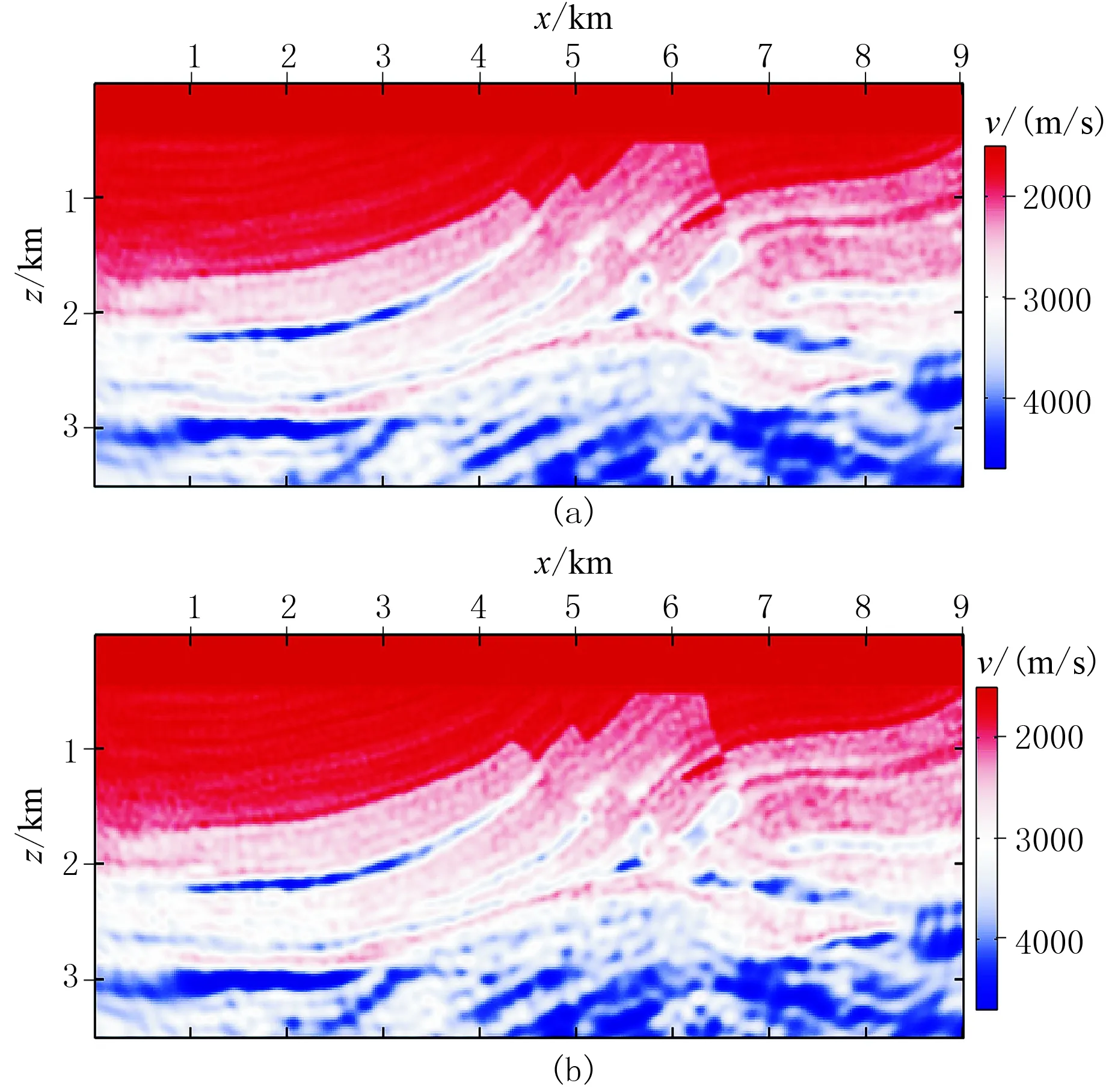
图A1 含高斯白噪声地震数据的反演结果 (a)应用Kaiser准则; (b)只应用第一主成分
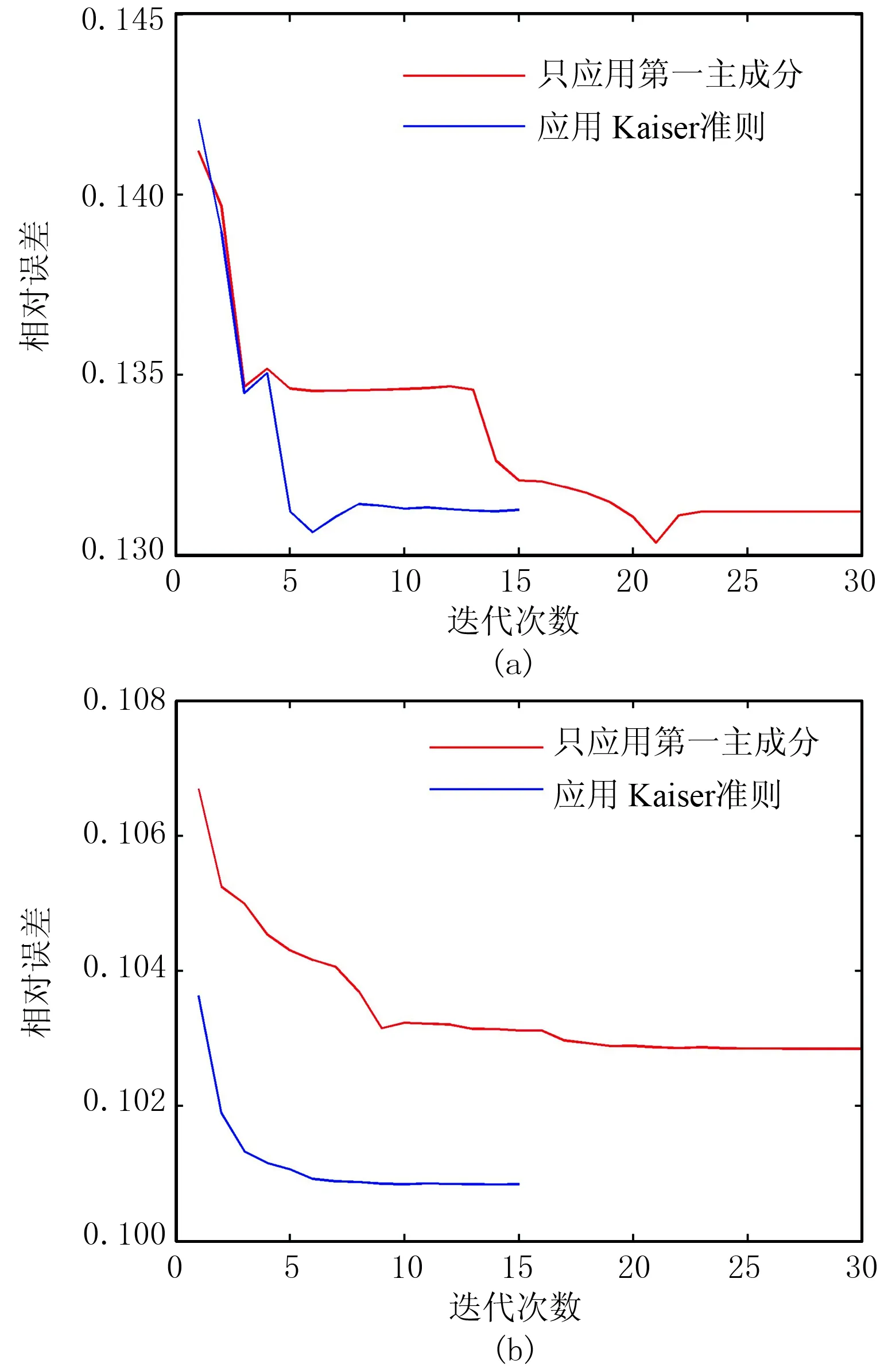
图A2 含高斯白噪声地震数据的反演相对误差曲线 (a)2.0Hz; (b)8.125Hz表A1 含高斯白噪声地震数据的反演相对误差对比

频率/Hz2.02.52.755.6258.12511.25应用Kaiser准则0.1310.1270.1180.1080.1010.099只应用第一主成分0.1310.1270.1180.1100.1030.101
[1] Tarantola A.Inversion of seismic data in acoustic approximation.Geophysics,1984,49(8):1259-1266.
[2] Bunks C,Saleck F M,Zaleski S et al.Multiscale seismic waveform inversion.Geophysics,1995,60(5):1457-1473.
[3] Pratt R G.Seismic waveform inversion in the frequency domain,Part 1:Theory and verification in a physical scale model.Geophysics,1999,64(3):888-901.
[4] Shin C,Cha Y H.Waveform inversion in the Laplace domain.Geophysical Journal International,2008,173(3):922-931.
[5] Sirgue L,Etgen J T,Albertin U.3D frequency domain waveform inversion using time domain finite difference methods.EAGE 70th Conference and Technical Exhibition,2008.
[6] Bekara M,Van der Baan M.Local SVD/ICA for signal enhancement of pre-stack seismic data.EAGE 68th Conference and Technical Exhibition,2006.
[7] 沈鸿雁,李庆春.频域奇异值分解 (SVD) 地震波场去噪.石油地球物理勘探,2010,45(2):185-189. Shen Hongyan,Li Qingchun.SVD(singular value decomposition) seismic wave field noise elimination in frequency domain.OGP,2010,45(2):185-189.
[8] 高静怀,毛剑,满蔚仕等.叠前地震资料噪声衰减的小波域方法研究.地球物理学报,2006,49(4):1155-1163. Gao Jinghuai,Mao Jian,Man Weishi et al.On the denoising method of prestack seismic data in wavelet domain.Chinese Journal of Geophysics,2006,49(4):1155-1163.
[9] 张恒磊,刘天佑,张云翠.基于高阶相关的 Curvelet 域和空间域的倾角扫描噪声压制方法.石油地球物理勘探,2010,45(2):208-214. Zhang Henglei,Liu Tianyou,Zhang Yuncui.High order correlation based dip angle scanning noise elimination method in Curvelet domain and space domain.OGP,2010,45(2):208-214.
[10] 张华,陈小宏,李红星等.曲波变换三维地震数据去噪技术.石油地球物理勘探,2017,52(2):226-232. Zhang Hua,Chen Xiaohong,Li Hongxing et al.3D seismic data de-noising approach based on Curvelet transform.OGP,2017,52(2):226-232.
[11] Tarantola A.Inverse Problem Theory:Methods for Data Fitting and Model Parameter Estimation.Elsevier,Amsterdam and New York,1987.
[12] Hugues A D,Tarantola A.Multiparameter L1norm waveform fitting: interpretation of Gulf of Mexico reflection seismograms.Geophysics,1999,64(4):1023-1035.
[13] Ha T,Chung W,Shin C.Waveform inversion using a back-propagation algorithm and a Huber function norm.Geophysics,2009,74(3):R15-R24.
[14] Bube K P.Hybrid L1/L2minimization with applica-tions to tomography.Geophysics,1997,62(4):1183-1195.
[15] Brossier R,Operto S,Virieux J.Robust elastic frequency-domain full-waveform inversion using the L1norm.Geophysical Research Letters,2009,36(20):L20310.
[16] 成景旺,吕晓春,顾汉明等.基于柯西分布的频率域全波形反演.石油地球物理勘探,2014,49(5):940-945. Cheng Jingwang,Lü Xiaochun,Gu Hanming et al.Full waveform inversion with Cauchy distribution in the frequency domain.OGP,2014,49(5):940-945.
[17] Oh J W,Min D J.Robust scaling strategy for frequency-domain acoustic full waveform inversion.ASEG 23rd Geophysical Conference Extended Abstracts,2013,1-4.
[18] Brossier R,Operto S,Virieux J.Which data residual norm for robust elastic frequency-domain full waveform inversion?.Geophysics,2010,75(3):R37-R46.
[19] Oh J W,Min D J.Spectral filtering of gradient for L2-norm frequency-domain elastic waveform inversion.Geophysical Journal International,2013,193(2):820-840.
[20] Kwon T,Seol S J,Byun J.Reduction of noise effect on elastic full-waveform inversion by using plane-wave data.SEG Technical Program Expanded Abstracts,2016,35:1131-1135.
[21] 苗永康.基于L-BFGS算法的时间域全波形反演.石油地球物理勘探,2015,50(3):469-474. Miao Yongkang.Full waveform inversion in time domain based on limited-memory BFGS algorithm.OGP,2015,50(3):469-474.
[22] Shin C,Jang S,Min D J.Improved amplitude preservation for prestack depth migration by inverse.Geophysical Prospecting,2008,49(5):592-606.
[23] Ben-Hadj-Ali H,Operto S,Virieux J.An efficient frequency-domain full waveform inversion method using simultaneous encoded sources.Geophysics,2011,76(4):R109-R124.
[24] 王学民.应用多元分析.上海:上海财经大学出版社,2014,251-256.
[25] Liu C,Han M,Han L et al.Application of principal component analysis for frequency-domain full waveform inversion.SEG Technical Program Expanded Abstracts,2012,31:1-5.
[26] 段超然,韩立国.主成分分析波场重构反演与全波形反演联合速度重构.石油地球物理勘探,2016,51(6):1134-1140. Duan Chaoran,Han Liguo.A joint velocity reconstruction method: principal component analysis based wavefield-reconstruction inversion combined with full waveform inversion.OGP,2016,51(6):1134-1140.
[27] 王凌群,李冰冰,林君等.航空电磁数据主成分滤波重构的噪声去除方法.地球物理学报,2015,58(8):2803-2811. Wang Lingqun,Li Bingbing,Lin Jun et al.Noise removal based on reconstruction of filtered principal components.Chinese Journal of Geophysics,2015,58(8):2803-2811.
[28] Zhu K G,Ma M Y,Che H W et al.PC-based artificial neural network inversion for airborne time-domain electromagnetic data.Applied Geophysics,2012,9(1):1-8.

