基于NGSIM数据的车辆瞬时速度获取方法
刘东亮,王秋爽
(1.东北师范大学 信息科学与技术学院,长春 130021;2.吉林大学学报(信息科学版)编辑部,长春 130012;3.吉林大学 计算机科学与技术学院,长春 130012)
科学的交通协同策略和管控措施需要准确的情报信息支撑,因此交通信息的采集成为交通研究过程的重要基础和关键环节。交通信息采集方法中,对视频和无线传感的相关研究较多。其中,基于视频识别的交通信息采集方法由美国加利福尼亚州的喷气推进实验室(Jet propulsion laboratory)于1978年首先提出,随后欧洲、日本也开始了对该领域的研究[1]。近十年,我国也开始重视交通信息的视频识别技术,许多专家学者对该领域进行了多方面的研究,取得了一系列成果[2-7]。基于无线传感网络(WSN)的交通信息采集方法,最早由美国加州大学伯克利分校的Bajwa等[8]进行研究并将其应用于交通领域,当前在该领域国内外已有相当多的研究与应用。此外,国内外还有学者研究了依靠图像信息参数进行车辆速度判别的方法,如王祺等[9]分析了不同车头间距下车速的分布规律,利用对数正态分布和负指数分布对交通流速度统计建模。Leitloff等[10]深入分析了遥感系统中全色影像与多波段影像的生成时刻,提出了一种利用全色-多光谱影像采集时间差推导车速的方法,文献[11,12]在重点进行图像处理的基础上利用该方法进行了交通信息采集研究,取得了一定成果。
虽然交通信息采集方法较多,若应用于大范围单车运行信息采集,上述方法仍有各自的不足:①对车头间距与车速相关性的研究尚滞留在统计层面,虽得到不同车头间距区间内速度的概率分布,但并未找到车头间距与车速间的严格映射关系,无法直接应用于广域交通信息采集;②基于遥感成像时间差的车速判别方法,必须以获取全色-多光谱影像采集时间差为前提,而该参数并非遥感系统的主要参数因而极难获取,笼统地使用文献[10]中的参数值将严重影响车速识别的精度。
针对统计方法所建映射关系不可直接应用、基于全色-多光谱时间差采集方法关键参数难以获取的现状,本文以NGSIM数据为基础数据,使用BP神经网络确定了被检测交通区域中车头间距、车辆轮廓两个图像信息参数与瞬时车速之间的映射关系,分析了瞬时车速随车头间距、车辆轮廓的变化趋势,建立了基于图像信息参数的瞬时车速模型,使用相近时间段的数据进行了模型验证,通过输出车速与实际车速的绝对平均误差证明了模型的可用性,并进一步分析了适用于本瞬时车速模型的车辆类型。
1 NGSIM数据
NGSIM(Next generation simulation)是由美国联邦高速公路管理局启动的下一代交通仿真工程,其收集、处理了大量的道路交通数据,为中微观交通研究提供了可靠、海量的数据源。NGSIM可为用户提供包含车长、车宽、车头间距、车辆速度等数据的“vehicle-trajectory-data”数据包。数据包中的数据由视频处理技术直接得到,因而能够反映目标车辆的瞬时状态,且初处理得到的车辆状态参数与目标车辆也保持高度一致。因此,本文选择NGSIM的“vehicle-trajectory-data”数据包作为模型建立的原始数据。
2 参数选择与数据处理
本文将NGSIM提供的“vehicle-trajectory-data”数据包作为模型建立的原始数据,数据采集位置分别为道路状况相近的US-101 Hollywood Freeway段(美国101快速路洛杉矶段)和I-80 Emeryville段,采集时间分别为2013年6月15日的8:20~8:35和2013年4月13日的17:15~17:30两个高峰时段。每个“vehicle-trajectory-data”数据包约有100万条数据记录,共分18个项目。数据项目见表1。

表1 数据项目Table 1 Data items
2.1 参数选择
(1)车头间距(Headway)
非线性跟驰理论认为,反应强度系数与车头间距成反比[13],即:
λ=λ1/s(t)=λ1/[xn(t)-xn+1(t)]
式中:λ为反应强度系数;λ1为常量参数;s(t)为t时刻车辆间的车头间距;xn(t)为t时刻n车的位置;xn+1(t)为t时刻n+1车的位置。
反应强度系数是根据前车所做的加速或减速运动而对后车进行的相应操纵行为及其效果。车头间距与反应强度成反比,反应强度对瞬时车速有影响,而车头间距也可由图像获取,因此选择车头间距Headway作为模型的输入参数。
(2)轮廓指数(Outline)
由于车辆性能和驾驶员行为的差异性,当车头间距相同时,不同的车辆会采取不同的跟驰速度[14],因而引入反映车辆性能的参数将提高模型的精度。车辆长度、车辆宽度均反映车辆轮廓情况,与车辆的型号及动力性有关,为减少输入参数的数量,定义车长与车宽之和为车辆轮廓指数并作为模型的输入参数:
Outline=Length+Width
式中:Outline为车辆轮廓指数;Length为车辆长度;Width为车辆宽度。
2.2 数据处理
(1)数据筛选
NGSIM中数据来源于美国高速公路,车辆种类包括摩托车、小型汽车和卡车。对于不同类型的车辆,外廓尺寸与车辆动力性的对应关系差别较大,为排除摩托车和卡车对模型造成的干扰,研究中仅使用Class项为2(小型汽车)的数据记录。
车头间距过大、车速过高说明车辆处于自由流状态,相邻车辆间的影响极小。而车头间距过小、车速过低则说明交通流处于阻塞状态,两种情况下图像信息参数与瞬时车速的映射关系均不明显[15]。为使模型更准确,选择车头间距为[5,200]m,车速为[30,70]km/h。
NGSIM未对车辆换道情况及换道时各图像信息参数进行详细的记录,无法研究换道跟驰现象,且由于外侧车道车辆数量较少,仅使用内侧1车道的数据,并将US-101 Hollywood freeway段2013年6月15日8:20~8:35时间段内的数据作为基础数据;将I-80 Emeryville段2013年4月13日17:15~17:30段内的数据作为模型验证数据。针对基础数据与模型验证数据两部分数据均根据车头间距与车速范围指标进行了筛选,将符合指标的数据用于后续的神经网络训练及模型验证。
(2)数据的归一化处理
由于本文拟使用神经网络进行建模,神经网络以样本在事件中的统计分布几率进行训练和预测,而当所有样本的输入信号都为正值时,与第一隐含层神经元相连的权值只能同时增加或减小。此外,由于一般神经网络将Sigmoid 函数作为传递函数,其值域为(-1,1)或(0,1),网络的输出也是如此,若不进行归一化处理,将导致学习速度变慢。为提高训练网络的收敛性,加快网络学习速度,需对输入输出数据(见表2)进行归一化处理,使数据的均值接近于0或与其均方差相比很小。

表2 输入和输出参数Table 2 Input and output parameters
本研究所用数据均为正值,因而对车辆轮廓指数、车头间距、车速数据使用线性函数转换方法按如下公式进行归一化处理:
y=(x-MinValue)/(MaxValue-MinValue)
式中:x为转换前数值;y为转换后数值;MaxValue为样本最大值;MinValue为样本最小值。
3 BP神经网络的建立
由跟驰理论可知,车辆速度、加速度、车头间距、驾驶员反应时间之间并非互不相干的独立关系,因而基于图像参数的车速模型是非线性模型。考虑到BP神经网络具有较强的海量数据处理和非线性拟合能力,本文采用BP神经网络建立以图像参数为输入的车辆瞬时速度模型。
3.1 BP网络结构确定
已证明任何一个连续函数均可由一个3层神经网络以任意精度逼近,含有一个隐含层的3层BP神经网络即可满足输入参数到输出参数的非线性映射。因此,本文选择使用3层BP神经网络结构。
一般利用试凑法确定隐含层节点数。试凑时,采用经验公式进行隐含层节点数的初步选择[16]:
式中:m为隐含层节点个数;n为输入层节点个数;l为输出层节点个数;α为1至10之间的常数。本研究中输入层节点数为2,输出层节点数为1,由于车辆轮廓指数的存在使映射关系变得复杂,本实验中取α为4,得到隐含层节点数为6。
3.2 传递函数确定
Sigmoid型函数不同于Pureline等线性阈值函数,其连续可微,适合作为传递函数用于隐含层(见图1)。具体到本研究,输出参数均为正值,应使用log-sigmoid单极性传递函数:
图1 Log-sigmoid与Purelin函数曲线Fig.1 Log-sigmoid and Pureline function curves
若BP 网络的输出层为Sigmoid 型函数,则网络的输出将被限制在(0,1)内,因而选择Pureline 型函数作为网络的输出层函数,使训练后的网络可输出任意值:
fpurelin(x)=x
3.3 训练方法确定
梯度下降动量(Gradient descent with momentum backpropagation)算法可避免最速梯度下降算法(Gradient descent backpropagation,GDB)陷于局部极小的情况,并可调节学习速率从而提高算法的可靠性和收敛性[17]:
wij(k+1)=wij(k)+η[(1-
α)d(k)+αd(k-1)]
式中:d(k)为k时刻的负梯度,d(k-1)为k-1时刻的负梯度,η为学习速率,α为动量因子。
α∈[0,1] ,当α=0时,权值修正只与当前负梯度有关,当α=1时,权值修正完全取决于上一次循环的负梯度。此方法加入的动量项相当于阻尼项,可以减小学习过程的震荡趋势,改善收敛性。
虽然梯度下降动量算法收敛速度较慢且需要较多的存储空间,但本研究非实时数据处理,对存储空间和收敛速度无特殊要求,选择有动量的梯度下降算法(GDM)作为网络训练方法。
4 网络训练与仿真验证
4.1 神经网络训练
将初处理后神经网络训练数据组中的车头间距Headway和车辆轮廓指数Outline作为输入,车速Velocity作为输出,规定最大训练次数为1000,使用表3所示BP神经网络参数,经多次调整确定隐含层节点数为10,训练后两个BP神经网络以0.0527的均方误差达到终止条件,作为反映输入输出参数映射关系的瞬时车速模型。
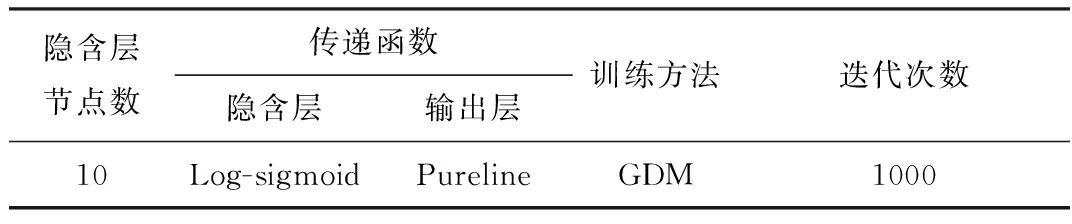
表3 BP神经网络结构参数Table 3 BP neural network structure parameters
4.2 仿真验证与结果分析
图2和图3分别是模型的仿真网格图和效果验证图。以各变量1%的步长形成模型曲面,仿真曲面反映出如下趋势:轮廓最大的车辆在车头间距最小时速度最慢;轮廓最小的车辆在车头间距最大时速度最快。车头间距与瞬时车速的正相关关系与王祺等[9]的统计结果一致。
将模型验证组中的图像信息数据输入训练后的神经网络中,输出两车道基于模型的瞬时车速,与相应实际车速对比,得绝对平均误差为13.73 km/h。
为详细分析误差产生原因,做出训练数据的车辆轮廓指数直方图与车速绝对平均误差(相应轮廓指数区间的MAE均值)曲线,如图4所示。
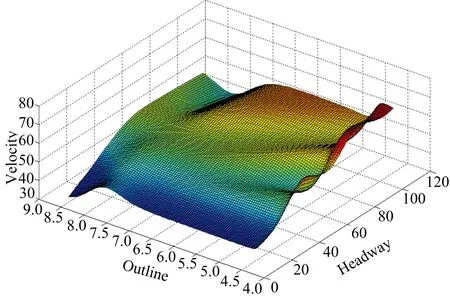
图2 模型仿真网格图Fig.2 Model simulation mesh diagrams
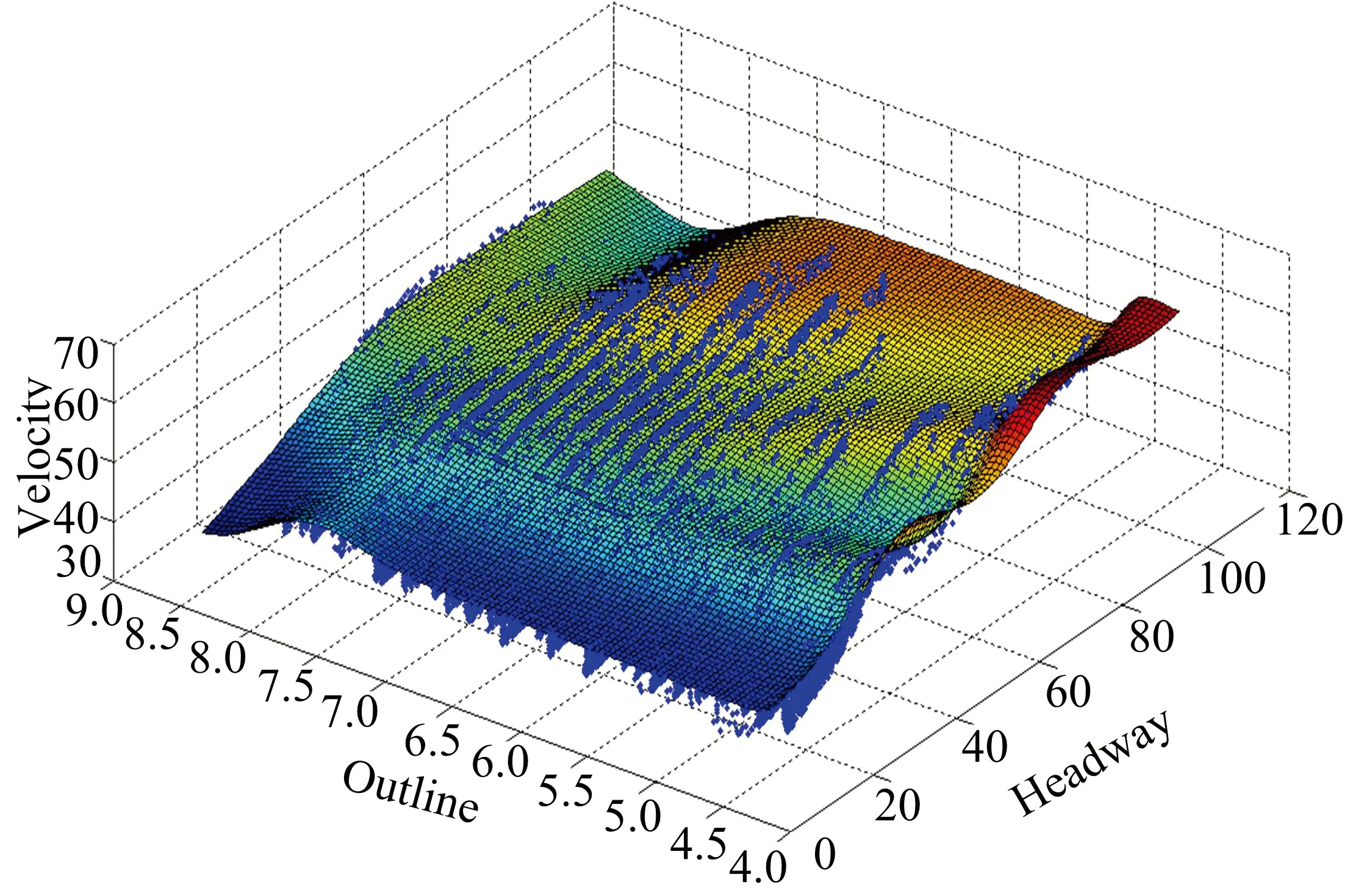
图3 模型效果验证图Fig.3 Model effect validation diagrams
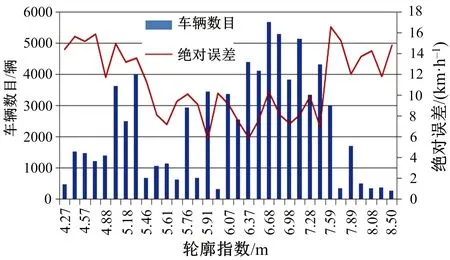
图4 轮廓指数直方图与车速MAE曲线Fig.4 Histograms of outline and waves ofvehicle speed MAE
轮廓指数是指车型车辆识别与分类的过程中大体的整车轮廓大小。由车辆轮廓指数直方图与车速绝对平均误差曲线可见:车辆轮廓指数集中分布在4.7~5.3 m和6.0~7.6 m的区间内;MAE曲线随不同轮廓指数的车辆数量变化,4.7~5.3 m和6.0~7.6 m区间内车速MAE较低,而其他车辆轮廓范围对应的车速MAE较高。
原因分析:
(1)进行BP神经网络训练时,轮廓指数在4.7~5.3 m和6.0~7.6 m区间内的车辆其样本量较大,神经网络的拟合效果较好;
(2)轮廓指数超过7.6 m的车辆,该类型车辆多为可进行货物运输车辆且发动机额定功率一般较大,使满载和空载时的加速能力等动力学参数产生明显差别,从而可造成不同样本情况下车速的较大差异。
5 结 论
(1)以NGSIM数据为基础数据,使用BP神经网络可确定被检测交通区域中车头间距、车辆轮廓两个图像信息参数与瞬时车速之间的映射关系。
(2)使用BP神经网络建立基于图像信息参数的瞬时车速模型可处理相近时间段的NGSIM数据,其输出车速与实际车速的绝对平均误差证明模型具有较高的可用性。
(3)仿真验证与分析结果表明,在US-101的NGSIM数据采集路段中,本文提出的车辆瞬时速度模型其总体准确性可以接受,且对轮廓指数为4.7~5.3 m和6.0~7.6 m区间内的中小型车辆较为适用。
(4)本文所做模型仿真实验是基于NGSIM数据样本进行的,将本文所提出的方法应用于实际情况时,为获得更好的效果,不应直接采用本文中NGSIM数据样本的训练结果,应针对应用环境下的交通数据流进行BP神经网络样本训练。
[1] 徐文聪. 基于视频的交通数据采集技术研究[D]. 山东大学机电与信息工程学院, 2012.
Xu Wen-cong. Research on the techniques of vision-based traffic data collection[D].Jinan:College of Mediatronics and Information Engineerig,Shandong University, 2012.
[2] Yin M, Zhang H, Meng H, et al. An HMM-based algorithm for vehicle detection in congested traffic situations[C]∥Intelligent Transportation Systems Conference,Seattle,WA,USA,2007: 736-741.
[3] Zhu Z, Xu G Y, Yang B, et al. VISATRAM: a real-time vision system for automatic traffic monitoring[J]. Image and Vision Computing, 2000, 18(10): 781-794.
[4] 李子青.人脸识别技术应用和市场分析[J].中国安防,2007(8):49-53.
Li Zi-qing . Face recognition technology and market analysis [J]. Security & Protection,2007(8):42-46.
[5] Tan T N, Sullivan G D, Baker K D. Model-based localisation and recognition of road vehicles[J]. International Journal of Computer Vision, 1998, 27(1): 5-25.
[6] Tai J C, Tseng S T, Lin C P, et al. Real-time image tracking for automatic traffic monitoring and enforcement applications[J]. Image and Vision Computing, 2004, 22(6): 485-501.
[7] Jin S, Wang D H, Xu C, et al. Short-term traffic safety forecasting using Gaussian mixture model and Kalman filter[J]. Journal of Zhejiang University (Science A), 2013, 14(4): 231-243.
[8] Bajwa R, Rajagopal R, Varaiya P, et al. In-pavement wireless sensor network for vehicle classification[C]∥10th International Conference on Information Processing in Sensor Networks (IPSN),Chicago,IL,USA,2011: 85-96.
[9] 王祺,李力,胡坚明,等.不同车头间距下交通流的速度分布[J].清华大学学报: 自然科学版,2011,51(3):23-26.
Wang Qi, Li Li, Hu Jian-ming, et al. Traffic velocity distributions for different spacings [J]. Journal of Tsinghua University(Science and Technology), 2011, 51(3): 309-312.
[10] Leitloff J, Hinz S, Stilla U. Inferring traffic activity from optical satellite images[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2007, 36(3/W49B): 89-93.
[11] 索明亮.卫星图像中运动车辆探测和速度提取研究 [D].北京: 北京交通大学城市交通复杂系统理论与技术教育部重点实验室,2011.
Suo Ming-liang. Research on moving vehicle detection and velocity extraction from satellite image [D].Beijing: MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology,Beijing Jiaotong University,2011.
[12] 张素兰.基于卫星遥感影像的交通状态判别研究 [D].北京: 北京交通大学交通运输规划与管理学院,2010.
Zhang Su-lan. Research on traffic state estimation from satellite remote sensing images [D].Beijing: College of Transportation Planning and Management,Beijing Jiaotong University,2010.
[13] 王殿海. 交通流理论[M]. 北京: 人民交通出版社, 2002:52.
[14] Bonzani I, Mussone L. From the discrete kinetic theory of vehicular traffic flow to computing the velocity distribution at equilibrium[J]. Mathematical and Computer Modelling, 2009, 49(3): 610-616.
[15] Bando M, Hasebe K, Nakayama A, et al. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51: 1035-1042.
[16] 李孝安, 张晓缋. 神经网络与神经计算机导论 [M]. 西安: 西安电子工业出版社, 1994.
[17] Wang J, Yang J, Wu W. Convergence of cyclic and almost-cyclic learning with momentum for feedforward neural networks[J].IEEE Transactions on Neural Networks,2011, 22(8): 1297-1306.

