非对称变翼飞行器复合控制系统设计
郭建国,吴林旭,周 军
(西北工业大学精确制导与控制研究所,西安 710072)
0 引 言
传统的固定翼飞行器的优越性往往只是体现在具体的飞行任务和某些特定的飞行状态之上,这在许多情况下制约了飞行器的飞行性能。为适应不断发展和改变的战场环境的需要,变外形飞行器应运而生[1]。变外形飞行器可以通过适当的变形[2-3](如变后掠翼、变翼展和Z型翼等)来改变外形以获得当前任务或飞行状态下最优的气动性能[4-5],使飞行器能够更好地完成多种飞行任务,但是并没有考虑将其作为一种主动的控制方式[6]来进行研究。
目前,对于变体飞行器,已有其建模、动力学特性[7-10],以及变翼飞行器姿态控制的研究。文献[11]针对变翼飞行器在变形过程中外形大幅变化的问题设计了自适应控制。文献[12]对一种多用途变体飞行器设计了鲁棒控制器。文献[13]使用自适应控制实现了对变体飞行器俯仰通道的跟踪,然而以上研究是基于飞行器模型已知的情况并且也没有考虑外界扰动影响。文献[14]针对变翼飞行器的LPV模型设计了鲁棒H∞控制器。以上研究主要是针对变形过程中带来的参数时变和一些附加干扰设计控制器,均没有将变翼作为一种主动控制方式开展研究。文献[15]研究了对称变翼展辅助机动情况,但未考虑非对称变化情况。此外,对于采用非对称变翼作为复合控制而言,需要进一步考虑控制指令分配问题,因为这直接关系到控制系统的性能[16-18]。
本文将非对称变翼作为一种新的主动控制方式,将传统的气动舵面操纵与机翼变形控制相结合建立了飞行器的姿态动力学模型[6,1-20],该模型是一个强耦合非线性的复合控制系统,且系统的气动参数亦会随着机翼变形而发生剧烈变化[10,20]。为此,对于机翼变形对系统结构和参数的影响以及其它外界扰动,选择滑模控制方法[21-23]联合扩张干扰观测器[24]设计复合控制器[25],实现对飞行器姿态的有效跟踪。
1 非对称变翼飞行器的姿态运动模型
非对称变翼飞行器的姿态模型[19-20]如下
(1)
(2)
(3)
(4)
(5)
式中Riy和Riz(i=1,2,3,4)为机翼运动和机翼与飞行器本体耦合所引起的附加力,具体形式为
(6)
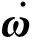
f2=-J-1ω×(Jω)
(7)
d2=J-1(M1+M2+M3+M4)
(8)
其中Mi(i=1,2,3,4)为质心的偏移,质量分布的变化和机翼运动以及机翼运动与飞行器转动的耦合所引起的附加力矩,r12×和r13×为相应矢量的叉乘矩阵,各附加力矩的表达形式如下:
(9)
非对称变翼对飞行器滚转通道的性能有很大提升[8,18,20],据此本文将机翼非对称变形做为一种新的主动控制加入到飞行器的姿态控制中。
2 控制分配
相比于传统的飞行器,非对称变翼飞行器姿态控制系统是一个复合控制系统。对于这样的复合控制系统,就需要设计复合逻辑对其控制量进行合理分配,同时还要保证复合逻辑适合实时计算,并且计算量不宜太大。期望的滚动力矩可以表示为Mxc=Mx,δx+Mx,δs其中Mxc表示为期望的滚转力矩,Mx,δx和Mx,δs分别为滚转舵偏和机翼的非对称变化所产生的滚转力矩。同时考虑到机翼的频繁响应会消耗大量的能量,产生不必要的干扰,所以引入死区特性,即在倾侧角的误差大于预设的阀值时机翼的非对称变化才开始响应[6],以避免机翼的频繁响应。记跟踪误差阀值为eU>eL>0,因此定义逻辑函数为
(10)
考虑如下非线性系统
x(n)=f(x)+g(x)u
(11)
控制u可以表示为u=u1+u2,定义[26]
u*=[-f(x)-KTx]/g(x)
(12)
式中:K=[k1,k2,…,kn]。将系统方程(11)表达成向量的形式并将式(12)代入则有
(13)
式中
(14)
(15)
定义李亚普诺夫函数如下
(16)
式中P是对称正定矩阵且满足李亚普诺夫方程
ΛTP+PΛ=-Q
(17)
式中Q是正定矩阵,因为Λ是稳定的,所以满足条件的P矩阵总是存在的。
假设|f(x)|的上界和|g(x)|的下界分别为fU和gL(gL>0)对李亚普诺夫函数求导可得
(18)
定义
u2=-ξsgn(xTPb)-[(fU+|kTx|)gL]
(19)
选择ξ(ξ≥|u1|),代入其中可得
(20)
所以将机翼的控制定义为
(21)
(22)
ux=uδx+h(eγv)·uδs
(23)
3 引入干扰观测器
飞行器机翼变化时会产生额外附加项,会影响整机质量的分布特性,增加了飞行器动力学模型的复杂性。所以,引入干扰观测器对控制器进行补偿[27-29]。
对于非线性系统
(24)
其中,x∈Rn,f为已知的非线性函数,d为系统中的未知扰动和未建模特性,将扩张干扰观测器设计为
(25)
(26)
式中
(27)
(28)
其中b01=diag(2κ…2κ),b02=diag(κ2…κ2)。
定义李亚普诺夫函数为
(29)
对其求导为
(30)
由定义的参数形式可知,矩阵Ag的特征值为λAg=-κ,从而可得
(31)
(32)
式中
λ=μ/κ
(33)
因此,当增大参数κ的值,观测器就能减少估计扰动d的时间,同时干扰估计误差也会减小,因此干扰观测器能够对系统扰动实时动态补偿。
4 姿态控制系统设计
令e1=Ωc-Ω为姿态角的误差,定义
(34)
设计如下滑模面[30]
s1=s-s(0)e-at
(35)
s=cz1+z2
(36)
式中:c=diag(c1,c2,c3)为正定对角矩阵,其中ci>0(i=1,2,3);a>0。
对式(36)求导可得
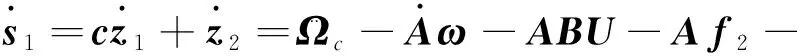
(37)
采用指数趋近律,则有
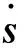
(38)
控制U的选择如下
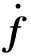
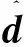
(39)
式中:k=diag(k1,k2,k3)为正定对角矩阵,其中ki>0(i=1,2,3);ε=diag(ε1,ε2,ε3)为正定对角矩阵,其中εi>0(i=1,2,3)。将式(39)代入式(37)可得
(40)
定义李亚普诺夫函数为
(41)
对其求导可得
(42)
当系统的状态在s1=0上运动时,由式(36)可知
z2=-cz1
(43)
将式(34)代入可得
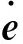
(44)
定义李亚普诺夫函数如下
(45)
求导可得
(46)
(47)
可见,状态误差e1是渐近稳定的。
5 仿真校验
设计非称变翼飞行器姿态控制系统仿真,通过跟踪期望指令来校验控制系统的控制效果,并且对只有传统气动舵面的的常规固定翼飞行器进行相同的仿真实验以作对比。同时,在对两种飞行器进行仿真的过程中,控制器参数保持不变。此外,采用蒙特卡洛法进行仿真验证,将气动力系数和气动力矩系数分别拉偏±40%和±30%。图1-3为攻角α、侧滑角β和倾侧角γV响应的对比曲线,图4-5为舵偏角变化对比曲线、倾侧角误差变化曲线以及机翼的变化曲线。图6-8为气动参数拉偏情况下姿态角跟踪的对比曲线。图9-11为在使用不同控制分配方法时,滚转舵偏,倾侧角响应曲线和机翼变化的对比图。
从图1可知,在采用同样的控制器及控制器参数的情况下,两种不同飞行器的攻角都可以跟踪相应的期望指令。二者的俯仰通道的上升时间和调节时间均相差不大,但是固定翼飞行器的超调量更大,达到了18%,而非对称变翼飞行器的超调量不到6%。图2表明,偏航通道中的侧滑角在整个控制过程中都在2°之内,但是对于固定翼飞行器而言,侧滑角的变化很剧烈,最大时接近6°,超出了控制系统的设计要求。由图3可以看出,两种飞行器滚转通道的上升时间相差不大,而非对称变翼飞行器的调节时间比固定翼飞行器的更小,并且超调量不超过5%,远小于固定翼飞行器。
从图4可以看出在倾侧角误差达到预设值之后,就要采用姿态复合控制系统。由图5可以看出,机翼的不对称变化使得气动舵面不会产生舵面饱和。
从图6-8中可以看出,无论是正拉偏还是负拉偏,飞行器姿态角的跟踪状态变化基本一致。可以对攻角、侧滑角和倾侧角稳定跟踪,稳态误差在3%以内,超调量也较小,说明文中所设计的控制器对参数的摄动有较好的鲁棒性和适应性。
从图9中可以看出采用广义逆的控制分配方法是机翼的变化全程参与姿态的控制,而本文中所设计的逻辑函数方法只在满足预设条件下机翼的变化才会启动,减少了额外的能量消耗。此外,从图10中可见,二者上升时间相差不大,然而采用逻辑函数方法时超调量略小。就动态性能而言,两种方法差别并不大,本文中方法的主要是避免了机翼在控制过程中频繁参与响应这一问题。图11可见,相比于逻辑函数方法,在使用广义逆的分配方法时,滚转通道就会出现气动舵面饱和状态。
从图12和图13可知,干扰观测器可以有效估计不确定项,其模型中干扰项的估计误差会在0.12 s内收敛到0附近小邻域内。
6 结 论
本文将机翼的非对称变化作为一种控制方式,基于干扰观测器技术和滑模控制方法,设计了非对称变翼飞行器姿态复合控制系统,并提出了非对称变翼的使用条件,设计了控制分配策略。仿真结果表明,相比于传统的固定翼飞行器,将非对称变翼作为一种新的控制方式提升了飞行器飞行性能。也验证了所设计的复合控制器对参数的摄动和干扰有很好的鲁棒性,避免了机翼的频繁响应。
[1] Weisshaar T A. Morphing aircraft systems: historical perspectives and future challenges [J]. Journal of Aircraft, 2013, 50 (2): 337-353.
[2] Barbarino S, Bilgen O, Ajaj R M,et al. A review of morphing aircraft[J]. Journal of Intelligent Material Systems and Structures,2011,22(9):823-877.
[3] 乐挺,王立新, 艾俊强.Z型翼变体飞行器的纵向多体动力学特性[J]. 航空学报, 2010, 31(4): 679-686. [Yue Ting, Wang Li-xin Ai Jun-qiang. Longitudinal multibody dynamic characteristics of Z-wing morphing aircraft [J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(4): 679-686.]
[4] Pecora R, Amoroso F, Lecce L. Effectiveness of wing twist morphing in roll control [J]. Journal of Aircraft,2012, 49(6):1666-1674.
[5] Obradovic B, Subbarao K. Modeling of flight dynamics of morphing wing aircraft [J]. Journal of Aircraft, 2011, 48(2):391-402.
[6] 童磊. 不对称变后掠翼飞行器多刚体建模与飞行控制[D].合肥: 中国科学技术大学.2013. [Tong Lei. Multi-body dynamic modelling and flight control for asymmetric variable sweep aircrafts [D]. Hefei: University of Science and Technology of China, 2013.]
[7] Beaverstock C S. Effect of symmetric & asymmetric span morphing on flight dynamics[C]. AIAA Atmospheric Flight Mechanics Conference, Maryland, USA, January 13-17 2014.
[8] Chakravarthy A, Grant D,Lind R. Time-varing dynamics of a micro air vehicle with variable-sweep morphing[J].Journal of Guidance, Control, and Dynamics. 2012, 35(3):890-903.
[9] 张杰, 吴森堂. 一种变体飞行器的动力学建模和动态特性分析[J]. 北京航空航天大学学报, 2015, 41(1):58-64.[Zhang Jie, Wu Sen-tang. Dynamic modeling for a morphing aircraft and dynamic characteristics analysis [J]. Journal of Beijing University of Aeromautics and Astronautics, 2015, 41(1): 58-64.]
[10] 郭建国, 陈惠娟, 周军等.非对称伸缩翼飞行器动力学建模及特性分析[J]. 系统工程与电子技术, 2016, 38(8): 1951-1957. [Guo Jian-guo, Chen Hui-juan, Zhou Jun, et al. Dynamics modeling and characteristic analysis for vehicle with asymmetric span morphing wing [J]. Systems Engineering and Electronics, 2016, 38(8):1951-1957.]
[11] Nigam N, Zhang Y, Chen P, et al. Adaptive control and actuation system development for biomimetic morphing [C]. 24th AIAA/AHS Adaptive Structures Conference, San Diego,California, USA, January 4-8, 2016.
[12] Abdulrahim M, Lind R. Control and simulation of a multi-role morphing micro air vehicle [C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, California, USA, August 15-18, 2005.
[13] Gandhi N, Jha A, Monaco J, et al. Intelligent control of a morphing aircraft[C]. 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, Hawaii USA, April 23-26, 2007.
[14] 董朝阳, 江未来,王青. 变翼展飞行器平滑切换LPV鲁棒H∞控制[J]. 宇航学报, 2015, 36(11):1270-1278.[Dong Chao-yang, Jiang Wei-lai, Wang Qing. Smoothing switching LPV robust H∞ control for variable-span vehicle [J]. Journal of Astronautics, 2015, 36(11): 1270-1278.]
[15] 殷明, 陆宇平, 何真等.变体飞行器变形辅助机构的建模与滑模控制[J].系统工程与电子技术, 2015, 37(1), 128-134. [Yin Ming, Lu Yu-ping, He Zhen, et al. Modeling and sliding mode control of morphing aircraft for morphing-aided maneuver [J]. Systems Engineering and Electronics, 2015, 37(1): 128-134.]
[16] 王磊, 王立新, 贾重任. 多操纵面飞翼布局作战飞机的控制分配方法[J]. 航空学报, 2011, 32(4):571-579.[Wang Lei, Wang Li-xin, Jia Zhong-ren. Control allocation method for combat flying wing with multiple control surfaces [J]. Acta Aeronautoca et Astronautica Sinica, 2011, 32(4): 571-579.]
[17] Ma C, Wang L. Flying-wing aircraft control allocation[C].47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, Florida, USA, January 5-8, 2009.
[18] 郭建国, 张添保, 周军等. 可重复使用飞行器归一化复合控制系统设计[J]. 宇航学报, 2016, 37(6):639-645.[Guo Jian-guo, Zhang Tian-bao, Zhou Jun, et al. Compound control system design for RLV based on normalization method [J]. Journal of Astronautics, 2016, 38(8): 1951-1957.]
[19] 杨贯通. 变外形飞行器建模与控制方法研究[D].北京:北京理工大学, 2015.[Yang Guan-tong. Research on modeling and control of morphing flight vehicles [D]. Beijing: Beijing Institute of Technology, 2015.]
[20] 毕胜. 变结构飞行器的多刚体建模和姿态控制[D].合肥: 中国科学技术大学, 2010. [Bi Sheng. Multi-rigid-body modeling and attitude control of variable structure aircraft [D]. Hefei: University of Science and Technology of China, 2010.]
[21] Lee Y, Kim Y, Moon G, et al. Sliding-mode based missile integrated attitude control schemes considering velocity change[J]. Journal of Guidance, Navigation Control, and Dynamics, 2016, 39(3): 423-432.
[22] 刘宇超,郭建国, 周军.基于新型快速Terminal滑模的高超声速飞行器姿态控制[J].航空学报, 2015, 36(7):2372-2380. [Liu Yu-chao, GuoJian-guo, Zhou Jun, et al. Hypersonic vehicle attitude control based on new fast terminal sliding mode [J]. Acta Aeronautoca et Astronautica Sinica, 2015, 36(7): 2372-2380.]
[23] Mattei G, Monaco S. Nonlinear autopilot design for an asymmetric missile using robust back stepping Control[J]. Journal of Guidance, Control and Dynamics, 2014, 37(5): 1462-1476.
[24] Zeng C, Tsourdos A, Lone M. Disturbance observer based sliding mode controller design for large civil aircraft. AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, USA, August 19-22, 2013.
[25] 毕永涛, 王宇航, 姚郁. 直/气复合控制导弹的模型预测和自抗扰姿态控制设计[J]. 宇航学报, 2015, 36(12):1373-1383. [Bi Yong-tao, Wang Hang-yu, Yao Yu. Attitude control design of missiles with dual control based on model predictive control and active disturbance rejection control. [J]. Journal of Astronautics, 2015, 36(12):1373-1383.]
[26] Wang L. A supervisory controller for fuzzy control systems that guarantees stability [J]. IEEE Transaetions on Automatic Control,1994, 39(9): 1845-1847.
[27] 韩京清. 自抗扰控制技术:估计补偿不确定因素的控制技术[M].北京: 国防工业出版社, 2008.
[28] 刘晓东, 黄万伟, 禹春梅. 含扩张状态观测器的高超声速飞行器动态面姿态控制[J]. 宇航学报, 2015,36(8):916-922. [Liu Xiao-dong, Huang Wan-wei, Yu Chun-mei. Dynamic surface attitude control for hypersonic vehicle containing extended state observer [J]. Journal of Astronautics, 2015, 36(8): 916-922.]
[29] 郭宗易, 周军, 郭建国. 新型高超声速飞行器耦合姿态控制系统设计[J]. 宇航学报, 2017, 38(3):270-278. [Guo Zong-yi, Zhou Jun, Guo Jian-guo. Novel coupling based attitude control system design for hypersonic vehicles [J].Journal of Astronautics, 2017, 38(3):270-278.]
[30] Ginoya D, Shendge P, Phadke S. Sliding mode control for mismatched uncertain systems using an extended disturbance observer[J].IEEE Transactions on Industrial Electronics, 2014, 61(4):1983-1992.

