具有SGCMG系统的挠性卫星姿态机动控制及验证

袁 利，雷拥军, 姚 宁，刘 洁，朱 琦

(1. 北京控制工程研究所，北京100094；2. 空间智能控制技术重点实验室，北京100094)

0 引 言

敏捷卫星由于能够根据任务要求快速改变姿态指向、实现对目标的灵活探测，相比传统卫星具有很多优势。尤其在遥感载荷成像方面，姿态快速机动可极大提高卫星使用灵活性和观测效率，快速高效获取非星下点目标遥感数据，是当今世界遥感卫星的一大发展方向[1-3]。早期的敏捷卫星姿态快速机动控制方法研究主要针对刚体卫星，随着小型敏捷卫星在遥感领域的应用优势[2-3]，高分辨率高性能大型载荷卫星具有姿态快速机动能力成为趋势[4]。大型遥感卫星一般安装有大型挠性太阳翼，使得动力学呈现复杂特性[5]，给高性能控制带来挑战。

由于基于系统控制频带远低于挠性模态频率的设计方法也无法适应挠性卫星敏捷性要求，挠性航天器姿态快速机动控制问题越来越受到关注。一方面，为避免姿态机动激发挠性振动，依据挠性动力学特性开展了基于输入成形、控制力矩成形等技术[6-9]的大量研究；另一方面，针对挠性卫星参数不确定的控制问题，相关文献开展了鲁棒控制、自适应控制及智能控制的姿态机动控制方法研究[10-14]；此外，针对姿态机动过程中挠性振动快速抑制问题，也有不少文献对基于压电陶瓷作动器开展主动振动抑制研究[15-16]。由ETS-VI卫星在轨评估显示实际挠性频率与理论值可能存在10%～40%的偏差[17]，从而使得依赖挠性参数的成形技术应用效果会受到影响。此外，上述挠性卫星控制方法研究由于其算法及工程实现的复杂性，目前主要局限于理论或地面试验验证。

上述挠性卫星姿态机动控制相关研究仅关注方法层面，而对控制系统工程实现中包括时延在内的因素欠缺考虑。对于敏感器与执行机构为共位安装的挠性卫星姿态稳定控制，由于其模态自身阻尼，理论上在常系数PD控制下可使得挠性模态均为全局稳定，并可通过参数选取实现宽带控制[18]。而系统往往因陀螺采样、星上计算等实现过程中不可避免地引入纯时延[19]，在此情况下不合适的控制参数选择可使得部分挠性模态不稳定而影响姿态机动性能。

大型挠性卫星姿态快速机动性能还受到姿态控制力矩及角动量管理实现约束。控制力矩陀螺(Control moment gyro,CMG)具有力矩精度高、力矩与角动量大等特点，是大型快速机动航天器合适的执行机构选择。对于CMG系统，目前研究所提出的奇异规避操纵律主要有零运动奇异规避操纵律与鲁棒奇异规避操纵律两大类[20-23]。其中鲁棒奇异规避操纵律能较好地实现显奇异点规避，但其存在的固有“框架锁死”现象以及在奇异规避中引入的力矩扰动对挠性振动的激发都是挠性卫星姿态快速机动需要考虑的问题。文献[21]对单框架CMG系统操纵律研究进行了较为全面地综述，并指出在当时还没有一种可靠的、行之有效的SGCMG系统操纵律能应用于航天器姿态控制中。正因如此，文献[22]提出了单框架CMG和动量轮组合的控制策略，以期在CMG奇异时依靠动量轮实现控制力矩精确输出，但实际动量轮输出力矩均很小，因此在工程上对于姿态快速机动卫星是很难适用的。尽管文献[23]在奇异状态附近通过对待求逆矩阵非对角元素引入时变项，以间接地施加时变扰动力矩实现奇异规避且避免“框架锁死”现象发生，但时变项中的周期及幅值等变量参数合理选择以适应系统长期运行各种工况是工程应用的一大难点。

针对挠性卫星在轨姿态快速机动控制问题，本文开展了挠性卫星姿态机动控制方法研究，解决具有系统时延下的挠性航天器姿态机动控制器设计及姿态机动实现的两方面控制问题。结合PD控制与补偿控制相结合的姿态控制方式与基于经典频率分析方法的参数选择，设计了挠性卫星姿态机动跟踪控制器，实现系统时延下兼顾系统稳定性及宽带控制的目标。在采用控制力矩陀螺作为执行机构实现挠性姿态机动实现中，与现有文献思路不同，本文基于直接对控制力矩指令施加偏转而产生避免“框架锁死”的扰动力矩思路，提出一种物理意义直观且工程实现方便的基于力矩矢量调节奇异规避新型操纵律，解决CMG系统的奇异规避及规避中挠性振动易激发的问题。最后，给出所提出方法的在轨实际应用的实施效果。

1 挠性卫星系统动力学

1.1 星体姿态运动学与动力学

记星体姿态描述为四元数q，卫星姿态运动学方程为[20]

(1a)

(1b)

式中：qv∈R3为姿态四元数q的矢量部分，q4为q的标量部分，ω∈R3为星体角速度。

当卫星具有大型挠性太阳翼时，由中心刚体与挠性附件组成的系统动力学方程为[12]

(2a)

(2b)

式(2a)与式(2b)分别描述星体转动与挠性附件振动。式中：J∈R3×3为星体转动惯量，其为正定对称阵，η∈Rm为挠性模态坐标，m为挠性模态数，τ∈R3为执行机构施加于中心体上的力矩，F∈R3×m为挠性耦合系数阵，Ω∈Rm×m为对角形式的挠性模态频率阵，ξ为挠性模态阻尼系数，一般取为0.005。

1.2 控制力矩陀螺系统

由n(n≥4)个控制力矩陀螺所组成系统中的第i(i=1,…,n)个CMG在星体系下的角动量hi为以对应CMG框架角δi为变量的向量函数，可表示为

(3)

式中：h为单个CMG的角动量幅值(系统中各CMG角动量幅值均相同)，mki,nki(k=1,2,3)为仅与第i个CMG安装相关的常数。

记框架角组合δ=[δ1,δ2,…,δn]T，由式(3)可得CMG系统在星体下合成角动量Hcmg为

h(Msinδ+Ncosδ)In×1

(4)

sinδ=diag(sinδ1, …, sinδn)
cosδ=diag(cosδ1, …, cosδn)

对Hcmg(δ)求时间导数可得

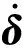
根据当前CMG系统的框架角及框架角速度，可得施加于星体的力矩为

(5)

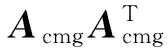
(6)

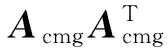
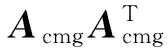
当sv越接近零表示系统越接近奇异状态，反之为系统远离奇异状态。

2 姿态机动控制器设计

卫星姿态机动跟踪足够光滑轨迹的期望姿态四元数qr与角速度ωr，由卫星当前姿态q与角速度ω，可得误差四元数qe为

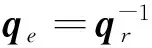
(7)

角速度误差ωe为

ωe=ω-C(qe)ωr

(8)

简写C(qe)为C，并记

τf=τ-(ωe+Cωr)×J(ωe+Cωr)+

由式(1)、式(2)、式(7)及式(8)可得基于误差四元数的运动学方程[24]

(9)

及动力学方程为

(10)

卫星挠性模态η信息一般为不可测，在动力学参数确知时类似挠性卫星姿态镇定PD控制[24]形式，可基于星体姿态及角速度信息设计如下姿态跟踪控制律为

τf=-2Kpqe vsgn(qe 4)-Kdωe

(11)

式中：控制参数Kp，Kd分别为比例与微分系数阵，一般选择为对角阵形式，sgn(·)为符号函数，即为

在星体期望运动角速度ωr下，由动力学方程(10)的挠性振动方程可求得标称轨迹下的标称挠性模态坐标为ηr，即

(12)

考虑姿态跟踪误差为小量时，即有qe v≈0且qe 4≈1，则C(qe)可近似为单位阵。记ηe=η-ηr，可将式(10)写为

(13)

记θ=2qe vsgn(qe 4)，当姿态跟踪误差为小量时由运动学方程(9)有

(14)

假设J具有主对角优势特性，故可忽略各轴间耦合，可按挠性卫星姿态稳定控制分析方式对由式(13)与式(14)所组成的跟踪系统各通道分别采用经典频域分析方法进行分析设计，以在考虑系统实现引入时延情况下选取兼顾模态稳定性及宽带控制的合适控制参数，尤其要避免过大参数选择使得部分模态不稳定情况发生。

(15)

式中：下标i(i=1,2,3)表示第i个通道，下标j(j=1,…,m)表示第j个挠性模态，e-Tds为系统纯时延环节传递函数，Ji为通道i的主惯量，其余变量为式(13)、式(14)中对应向量或矩阵的相应分量。

对式(11)取拉氏变换，得各通道控制器传递函数为

τf,i(s)=-(Kp,i+Kd,is)θi(s)

(16)

式中：Kp,i,Kd,i分别为Kp,Kd对应通道i的分量。

基于式(16) 所示控制形式，结合控制参数选取，可利用经典频域分析法对式(15)进行稳定性分析，以选择合适的控制参数Kp,Kd。

根据时延环节e-Tds的频率特性，其不对系统幅值特性产生作用，但会引入相位滞后，其相位滞后量与频率f的关系为

Δφ=2πf·Td

由此可见，时延对不同挠性模态频率处产生的相位滞后量随挠性模态频率呈线性关系。

对于式(15)所示单通道传递函数，以示例方式来说明挠性卫星在系统时延下的控制参数选择以及其对系统稳定性的影响。设对象转动惯量为3000 kg·m2且具有完全相同的两太阳翼，其挠性第一、二阶模态频率分别为0.31 Hz与1.35 Hz及对应耦合系数分别为20.06 kg0.5·m与20.06 kg0.5·m。针对式(16)控制形式选取两组控制参数值，其中控制参数组1为Kp,i=94与Kd,i=1350，控制参数组2为Kp,i=11.2与Kd,i=463。

针对系统无时延和系统有时延且时延常数Td=0.25 s两种情况，两组控制参数下开环系统传递函数的Nichols图如图1所示。由图1可知，在控制参数组1作用下无时延系统的第一、二阶挠性模态均为相位稳定；但当系统有时延后，若仍采取控制参数组1则系统第二阶挠性模态由于相位滞后过大出现不稳定现象，若降低控制参数而采用控制参数组2则该挠性模态成为增益稳定。因此，在系统具有时延情况下，选择过大控制参数可能使得系统挠性模态出现不稳定现象，控制参数选择直接受系统时延制约。

由于挠性模态自身阻尼低，当姿态快速机动挠性振动激发后很难短时间内由其自身阻尼衰减下来，故将低阶挠性模态设计为相位稳定，通过姿态控制为模态振动提供主动阻尼；对于高阶模态，鉴于系统时延影响及动力学建模不确定性，将其设计为增益稳定方式，其振动依靠自身结构阻尼衰减。在采用式(10)所示控制结构形式时，若无法选择到合适的控制参数(兼顾机动宽带控制且对挠性模态稳定)，可进一步引入不同形式结构滤波器[25],从而降低高阶不稳定挠性模态增益、适当增大低阶挠性模态相位裕度且保证一定幅频增益。

基于确定参数Kp,Kd，由式(11)计算得到τf，并考虑控制力矩陀螺角动量的陀螺力矩影响，从而可设计系统姿态控制力矩指令为

τr= -2Kpqe vsgn(qe 4)-Kdωe+

(17)

3 控制力矩陀螺操纵律设计

基于CMG系统奇异时无法沿奇异方向输出力矩几何解释及鲁棒奇异规避操纵律框架“锁死”现象的原理，文本提出了当框架构型临近或处于奇异状态时直接对指令力矩进行偏转的矢量调节思路，以脱离奇异状态且避免“框架锁死”。

定义矢量调节矩阵为

式中：υi(i=1,2,3)为指令力矩矢量调节系数，取为

(18)

式中：kυ,i为调节增益系数，vsv>0为调节阈值，sat(·)为饱和函数，即

饱和限幅值υLimt一般取为0≤υLimt<1。

控制力矩指令τr，对应的调节算法为

τAdj=AAdj·τr

(19)

从调节矩阵AAdj的形式来看，当υi为小量时则可将AAdj看作为方向余弦阵，系统在CMG系统奇异度量值较小时通过式(19)所示方式直接改变控制力矩指令τr方向，沿三个方向旋转角度为υi。由所设计式(18)的形式可知，υi随奇异度量值sv相应自主调整，当sv值越小则|υi|越大，意味着τr偏转角度越大，从而实现力矩指令偏离奇异方向，保证有效脱离框架角奇异状态且避免常规鲁棒奇异操纵律存在的框架“锁死”现象发生。此外，通过矩阵AAdj调节运算后，力矩指令τr变化前、后之间具有如下关系

由此可保证在姿态机动规避奇异过程中调节得到的力矩指令τAdj与原指令τr之间夹角小于90°，避免卫星姿态机动时调节力矩指令与原力矩指令方向相反导致CMG系统角动量往返穿越奇异面而未能脱离的情况。在υi形式上采用限幅处理，避免偏差角度过大使得τAdj在垂直τr的平面内分量过大超出CMG实际框架转速输出限制的问题。

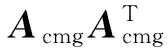
综上考虑，设计的基于矢量调节奇异规避操纵律为

(20)

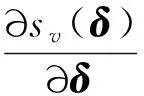
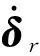
给定阈值vsv1与vsv2且满足vsv2≥vsv≥vsv1，基于上述引入各算法先后顺序及系数连续性设计思路，给出系数αs1,αs2的一种实现形式为[26]

式中：kαs1,kαs2为非负常数，αs10为非负常值偏置量，此处饱和函数sat(·)的饱和限幅为非负常数αs20。

4 在轨校验

结合某大型挠性卫星开展机动控制在轨校验。卫星两块太阳翼前两阶挠性模态标称频率分别为0.25 Hz与0.6 Hz。配置6个单框架控制力矩陀螺实现整星姿态控制，控制器参数设计选择中系统时延常数按0.25 s考虑。

4.1 机动控制校验

依照第2节给出的姿态控制形式及控制律参数选择方式设计出式(17)形式的姿态控制器，其中对于前两阶挠性模态采用相位稳定方式，其余高阶模态均为增益稳定。在帆板转角为45°时，含控制器环节的系统滚动通道开环Nichols图如图2所示(俯仰与偏航通道开环频率特性相似，此略)，其中第一阶挠性模态增益约为6 dB。

在所设计控制器下星体进行姿态机动，两次机动的星体姿态角速度及角速度误差如图3所示。从图3可以看出，在机动过程中挠性模态振动被有效抑制，姿态到位后角速度很快收敛至零附近。

在维持PD控制参数不变的基础上，引入陷阱滤波器使得前两阶挠性模态增益均在0 dB以下，即所有挠性模态均为增益稳定，对应系统滚动通道开环传函的Nichols图如图4所示。机动对应姿态角速度及角速度误差如图5所示，从图4～5可以看出，在机动过程中挠性模态振动明显，从而对星体机动到位后姿态稳定性能产生一定影响。

4.2 奇异规避校验

针对式(20)所示CMG奇异规避操纵律，设定vsv2=2，vsv1=0.3，vsv=0.7，即实现目的为：奇异度量值大于2时直接采用式(6)所示伪逆求解CMG框架角速度指令；当奇异度量值小于2时开始启动零运动奇异规避算法；当奇异度量值小于0.7时启用矢量调节算法；当奇异度量小于0.3时启用防奇异因子。其它参数选取为kυ,i=2，υLimt=0.7，kα s1=0.18，kα s2=0.1，αs10=0，αs20=0.5。

在6个CMG组合下进行姿态机动及机动返回的姿态角曲线如图6所示，在此过程中CMG的奇异度量值变化如图7所示。由图7可知，在姿态机动返回过程中，系统奇异度量值由7逐渐接近1，经零运动规避算法有效提升到2附近。

为验证矢量调节奇异规避算法的有效性，在轨采用5个CMG组合进行姿态机动，机动及机动返回的姿态角曲线如图8所示。

机动全过程CMG奇异度量值变化如图9所示。由图9可知，在滚动角姿态负向机动的初始阶段，尽管有零运动奇异规避作用，但随机动角速度增大奇异度量值快速下降到0.7以下，从而触发矢量调节算法，在达到0.1后迅速提升到0.7以上，并在零运动奇异规避持续作用下，最终将奇异度量值提升到2以上；在滚动正向机动时，初始阶段在零运动奇异规避作用下奇异度量值在2附近短时间波动，随着机动角速度增加奇异度量值迅速下降到0.7以下，在矢量调节算法作用下奇异度量值下降到0.4转为上升，并在零运动奇异规避作用下将奇异度量值提升至2附近。由于基于矢量调节的CMG奇异规避策略保证输出力矩连续变化，由图10可知，奇异规避过程中避免激发挠性模态振动。

5 结 论

为实现挠性卫星在轨姿态快速机动控制，本文设计了PD控制与补偿控制相结合的姿态跟踪控制器，并基于经典频率分析方法的参数选择，实现了具有系统时延下兼顾系统稳定性及宽带控制的目标。在基于控制力矩陀螺的挠性卫星姿态快速机动实现中，与传统奇异规避操纵律不同，采用直接对力矩指令偏转的矢量调节新型规避策略，实现奇异规避的同时可有效避免挠性振动激发。在轨验证结果表明，所提出方法可有效解决大型挠性卫星姿态快速机动的工程实现问题。

[1] 祝佳, 陶峰. 敏捷成像卫星需求筹划系统应用探析[J].电讯技术，2014, 56(5):508-516. [Zhu Jia, Tao Feng. Application discussion on agile spacecraft requirements planning system [J]. Telecommunication Engineering , 2014, 56(5):508-516.]

[2] 葛玉君, 赵键, 杨芳. 高分辨率光学遥感卫星平台技术综述[J]. 国际太空, 2013(5):2-8.[Ge Yu-jun, Zhao Jian, Yang Fang. Technical review of high resolution optical remote sensing satellite platforms [J]. Space International, 2013(5):2-8. ]

[3] 郭今昌. 商用高分辨率光学遥感卫星及平台技术分析[J]. 航天器工程, 2009, 18(2): 83-89. [Guo Jin-chang. Technical analysis of high resolution commercial optical remote sensing satellite [J]. Spacecraft Engineering , 2009, 18(2): 83-89.]

[4] 范宁, 祖家国, 杨文涛，等. WorldView系列卫星设计状态分析与启示[J]. 航天器环境工程, 2014, 31(3): 337-342. [Fan Ning, Zu Jia-guo, Yang Wen-tao, et al. The design of WorldView satellite and its demonstrative value [J]. Spacecraft Environment Engineering, 2014, 31(3): 337-342.]

[5] 耿长福. 航天器动力学[M]. 北京：中国科学技术出版社，2006.

[6] Byers R M, Vadali S R, Junkins J L. Near-minimum time ,closed-loop slewing of flexible spacecraft [J]. Journal of Guidance, Control and Dynamics, 1990, 13(1):57-65.

[7] Kamiya Y, Maeda K, Sakai S. Comparison of preshaping profilers for reducing residual vibrations after rest-to-rest maneuvers [J]. Journal of Guidance Control and Dynamics, 2015, 38(5): 874-885.

[8] 周伟敏, 廖瑛, 杨雅君，等. 一种应用输入成型的敏捷卫星快速姿态机动控制方法[J]. 航天器工程, 2016, 25(4): 27-32. [Zhou Wei-min, Liao Ying, Yang Ya-jun, et al. Attitude maneuver control method for agile satellite based on input shaping [J]. Spacecraft Engineering, 2016, 25(4): 27-32.]

[9] Chen H J, Agrawal B N. Method of slewing the spacecraft to minimize settling time [C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, California, USA, August 5-8 2002.

[10] Yu Y, Meng X, Li K, et al. Robust control of flexible spacecraft during large-angle attitude maneuver [J]. Journal of Guidance Control and Dynamics, 2014, 37(3):1027-1033.

[11] 管萍, 陈家斌, 刘向东. 基于自适应模糊与输入输出线性化的卫星姿态控制[J]. 控制与决策, 2004, 19(7): 741-745. [Guan Ping, Chen Jia-bin, Liu Xiang-dong. Variable structure control with time-varying sliding mode and vibration control for flexible satellite [J]. Control and Decision, 2004, 19(7): 741-745.]

[12] 雷拥军, 谈树萍, 刘一武. 一种航天器姿态快速机动及稳定控制[J]. 中国空间科学技术, 2010, 30(5):48-53. [Lei Yong-jun, Tan Shu-ping, Liu Yi-wu. Spacecraft control method for fast attitude maneuver and stabilization [J]. Chinese Space Science and Technology, 2010, 30(5):48-53.]

[13] 孙多青. 分层模糊广义预测控制及其在挠性航天器振动抑制中的应用[J]. 宇航学报, 2009, 30(4): 1537-1543. [Sun Duo-qing. Hierarchical fuzzy generalized predictive control and its application in vibration suppression of flexible spacecraft [J]. Journal of Astronautics, 2009, 30(4):1537-1543.]

[14] 耿云海, 吴炜平, 马玉海. 神经网络补偿的挠性卫星敏捷姿态机动[J]. 哈尔滨工业大学学报, 2012, 44(5): 741-745. [Geng Yun-hai, Wu Wei-ping, Ma Yu-hai. Neural network compensation of flexible satellite rapid maneuver [J]. Journal of Harbin Institute of Technology, 2012, 44(5):741-745.]

[15] Di Gennaro S. Active vibration suppression in flexible spacecraft attitude tracking [J]. Journal of Guidance Control and Dynamics, 1998, 21(3):400-408.

[16] 胡庆雷, 马广富, 姜野，等. 三轴稳定挠性卫星姿态机动时变滑模变结构和主动振动控制[J]. 控制理论与应用, 2009, 6(2): 122-126. [Hu Qing-lei, Ma Guang-fu, Jiang Ye, et al. Variable structure control with time-varying sliding mode and vibration control for flexible satellite [J]. Control Theory and Applications, 2009, 6(2):122-126.]

[17] Kida T, Yamaguchi I, Chida Y, et al. On-orbit robust control experiment of flexible spacecraft ETS-VI [C]. AIAA Guidance Navigation and Control Conference, San Diego, CA, July 29-31, 1996.

[18] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京：北京航空航天大学出版社, 1998.

[19] Wie B, Liu Q, Bauer F. Classical and robust H∞control redesign for the Hubble Space Telescope [C]. AIAA Guidance, Navigation and Control Conference, Hilton Head Island, SC, August 10-12, 1992.

[20] Kurokawa H. Constrained steering law of pyramid-type control moment gyros and ground tests [J].Journal of Guidance, Control, and Dynamics, 1997, 20(3): 445-449.

[21] 吴忠, 吴宏鑫. 单框架控制力矩陀螺系统操纵律研究综述 [J]. 宇航学报, 2000, 21(4): 140-145. [Wu Zhong, Wu Hong-xin. Survey on steering laws for single gimbal control moment gyroscope systems [J]. Journal of Astronautics, 2000, 21(4):140-145.]

[22] 金磊, 徐世杰. 采用单框架控制力矩陀螺和动量轮的航天器姿态跟踪控制研究 [J]. 宇航学报, 2008, 29(3): 916-921. [Jin Lei, Xu Shi-jie. Attitude tracking control of a spacecraft using single gimbal control moment gyros and momentum wheels [J]. Journal of Astronautics, 2008, 29(3): 916-921.]

[23] Wie B. Singularity escape/Avoidance steering logic for control moment gyro system [J]. Journal of Guidance, Control, and Dynamics, 2005, 28(5):948-956.

[24] Costic B T, Dawson D M W, De Queiroz M S, et al. A quaternion-based adaptive attitude tracking controller without velocity measurements [C]. The 39th IEEE Conference on Decision and Control, Sydney, Australia, December, 2000.

[25] Wie B, Byun K W. New generalized structural filtering concept for active vibration control synthesis [J]. Journal of Guidance, 1989, 12(2):147-154.

[26] 孙羽佳, 袁利, 雷拥军. 基于指令力矩螺旋式搜索的SGCMG奇异规避方法[J]. 空间控制技术与应用, 2016, 42(6): 26-30. [Sun Yu-jia, Yuan Li, Lei Yong-jun. SGCMG singularity avoidance method based on command torque vector helix search [J]. Aerospace Control and Application, 2016, 42(6):26-30.]