基于纹理边界检测的航天器椭圆特征提取方法
王诗强,张世杰
(哈尔滨工业大学卫星技术研究所,哈尔滨150080)
0 引 言
由于视觉相对位姿确定系统具有精度高、质量轻、功耗低等特点,目前广泛应用于交会对接[1]、在轨服务[2]等任务中。
为保证上述任务的成功,需要持续地确定两航天器的相对位姿,许多学者利用目标上安装的特征靶标确定目标航天器的相对位姿[3-5]。但非合作目标无法安装特征靶标,因此需要利用目标上的自然特征确定相对位姿,这种方式的前提条件是提取目标图像中的自然特征。非合作目标上的自然特征主要包括直线特征和圆特征,对于大部分航天器而言,其星箭对接环和发动机喷管处包含可利用的圆特征,圆特征在图像中的投影为椭圆。与直线特征相比,椭圆特征在相对位姿确定中可用矩阵进行表示,便于数学处理,并且通常情况下能得到闭式解[6]。对于图像中椭圆特征的提取,Xu等[7]在获取图像边缘特征的基础上,采用随机霍夫变换方法提取图像中航天器上的椭圆特征,虽然随机霍夫变换与标准霍夫变换相比提高了提取速度,但是在实际应用中,速度仍然不理想。对此,一些学者利用椭圆长度、凹凸性和曲率等几何属性确定属于椭圆特征的边缘,通过判断这些边缘特征的相似性,对属于同一个椭圆特征的边缘进行组合[8-9],最后利用直接最小二乘法[10]拟合椭圆参数。这类方法由于排除了非椭圆边缘特征,减小了数据量,与随机霍夫变换相比提高了计算速度,但引入了大量的几何约束,导致这类方法的输入参数较多,在实际应用中,需要不断调整算法参数来适应椭圆形状的变化。基于梯度区域生长的方法是一种无参数的椭圆特征检测方法,该方法认为图像中的椭圆特征由图像中某些特殊区域组成,这些区域中像素的梯度具有相似的方向,如果若干相邻区域合并后,形状凹凸性保持不变,那么合并后的区域就可作为一个椭圆假设[11-12],最后根据(Number of false alarms,NFA)准则[13]确定椭圆特征。
上述方法均在图像的边缘特征或梯度信息基础上进行椭圆特征提取,由于航天器本体表面的隔热材料凹凸不平,在阳光照射下会在图像中产生明暗交替的纹理,这些纹理会使图像中原本连续光滑的边缘特征或梯度方向一致的区域出现断裂,导致上述方法难以准确提取对接环处的椭圆特征。为此,有必要探索新的椭圆检测算法。
纹理是图像的某种局部性质,是对局部区域中像素之间关系的一种度量,其像素灰度或色彩分布一般具有统计意义上的规律[14]。与边缘特征和梯度信息相比,利用纹理特征确定两区域的边界可避免纹理图案对边界的影响。目前利用纹理特征进行区域边界检测已广泛应用到图像分割领域,主要的方法包括:频谱法、模型法和统计方法。频谱法将图像变换到频域空间,在不同尺度和不同方向上对图像中的纹理进行分析,得到描述纹理的特征向量,最后将这些特征向量进行分类,实现不同纹理区域的分割,得到纹理边界[15]。这种方法需要进行多尺度、多方向运算,计算量较大,无法满足交会对接中椭圆特征检测的实时性要求。模型法中各纹理区域的灰度分布可表示成一个由多参数定义的模型,通过统计图像中各像素的灰度值确定各模型中的参数,从而实现纹理区域的分割,进而确定各区域之间的边界[16]。模型法是从各纹理区域灰度分布的全局特性出发,并不能较好地获得局部纹理之间的边界,因此不适用于对接环处椭圆特征的提取。统计法是从图像灰度的统计特性和整体出发,发现纹理存在的某种规律,其主要思想是通过图像中灰度级分布的随机属性来描述纹理特征,适用于描述不规则的自然纹理[17]。统计方法简单易于实现,但复杂度较高,限制了计算速度。
综上,本文以对接环处的圆特征为目标,利用航天器表面与对接环区域的不同纹理特性,探索新的利用纹理边界检测的快速椭圆特征提取算法,为验证算法的精度与快速性,开展仿真试验,并与典型方法进行对比验证。
1 问题描述
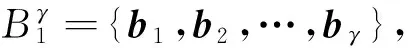
(1)
式中:η为归一化常数。
因此,提取图像中纹理边界点的问题就转化成求式(1)为最大值时bc的坐标的问题。
确定椭圆边界点像素仅解决了椭圆特征提取中像素点的归属问题,还需确定椭圆参数。直接最小二乘法是一种非迭代椭圆参数拟合方法。
拟合椭圆的数学模型为:
Ax2+Bxy+Cy2+Dx+Ey+F=0
(2)
式中:A,B,C,D,E,F分别为与椭圆中心坐标、长轴、短轴、长轴与图像坐标系横轴的夹角5个参数相关的系数。因此,上述模型包含5个未知量,当参与拟合的点数量不少于5时,利用带约束的最小二乘法即可确定A,B,C,D,E,F的值,进而求得椭圆的5个参数。
综上所述,式(1)和式(2)构成了椭圆特征检测的数学模型。
2 总体结构
如前所述,基于边缘特征和基于梯度区域生长的椭圆特征检测方法无法在具有纹理的图像中检测椭圆特征。因此,本文利用图像中的纹理特征,结合目标模型上的对接环尺寸r和上一时刻的相对位姿信息Rk-1和tk-1,从椭圆特征初始定位、边界点检测直线设置、纹理边界点提取、粗大误差去除四个方面,对目标航天器图像中的椭圆特征提取方法进行研究。
为了保证提取椭圆特征的准确性,首先在对接环所在空间圆上均匀取m个点Pi=[Pix,Piy,Piz]T,i=1,2,…,m,在已知目标模型的条件下,很容易获得这些点在目标上的位置。然后,利用上一时刻的相对位姿信息Rk-1、tk-1和相机参数矩阵K将这些空间点Pi投影到图像中。由于两时刻的相对位姿变化较小,因此这些投影点pi=[piu,piv]T在当前图像中椭圆边界的附近。至此,确定了椭圆特征的初始位置,并且建立图像中投影点与空间圆的对应关系。
为了检测图像中的椭圆边界点,首先,在每个投影点pi处建立边界检测直线,该直线的方向与pi-1和pi+1连线的中垂线平行,且具有足够的长度穿过纹理边界,设直线的长度为γ个像素。然后,利用式(1)计算直线上各点属于边界的概率,以令式(1)取最大值的点作为边界点。重复该过程,直到完成所有直线上边界点的检测。
为了去除粗大误差,进一步提高椭圆特征的精度,通过RANSAC方法去除边界点中的粗大误差点,以最佳一致点集为拟合数据,利用直接最小二乘法求解椭圆参数,算法的总体结构如图2所示。
3 椭圆特征提取算法
3.1 椭圆特征初始定位
对于星箭对接环上的点Pi=[Pix,Piy,Piz]T,i=1,2,…,m,利用式(3)将其变换到相机坐标系中:
Qi=RPi+t,i=1,2,…,m
(3)
式中:R为相对姿态矩阵,t=[tx,ty,tz]T为相对位置向量。
假设相机已经进行标定,内参数矩阵为K,对于相机坐标系中的点Qi=[xi,yi,zi]T,i=1,2,…,m,根据小孔相机模型,点Qi在图像中的投影pi可表示为:
(4)
式中:f为相机镜头的焦距,u0和v0为图像水平和垂直方向上的主点坐标,μ为像元尺寸。
根据上述投影理论,将对接环上的空间点投影到当前图像中,得到m个投影点。m越大,获得的边界点数量越多,拟合出的椭圆参数越精确,计算时间越长。为权衡精度与计算时间,令m=40。
3.2 设置边界点检测直线
第i条边界点检测直线由方向向量ki=[kiu,kiv]和投影点pi=[piu,piv]T确定,其中ki通过相邻两投影点连线的垂线获得,如下所示:
(5)
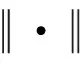
由于图像是由离散的像素点组成的,因此需要将搜索直线离散化,利用式(6),可计算出边界点检测直线上各点的坐标bi,j。
(6)
式中:i,j表示第i条边界点检测直线上的第j个点,γ表示边界点检测直线的长度。
根据bi,j的坐标,利用式(7)可获取该点处图像的灰度值si,j,并存储在集合Si中。
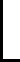
(7)
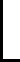
3.3 纹理边界点提取

(8)
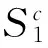
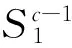
通过改变序号c的值,利用式(8)可计算出构成式(1)的两部分概率值,进而得到式(1)的值。使式(1)为最大值的序号c对应的点即为所求边界点,重复上述过程,直到完成所有边界点检测直线上边界点的提取。
3.4 粗大误差去除
采用RANSAC方法对边界点集合中的粗大误差点进行去除。RANSAC方法通过随机选择一组纹理边界点的方式寻找一致性最好的椭圆参数。由于直接最小二乘法拟合出的椭圆参数与数据点的坐标有关,如果这些数据点集中在一个区域,那么得到的椭圆参数将有较大的偏差。为了避免这种情况,将所有纹理变换点进行编号,并均匀分成4部分,在各部分内随机选取纹理变换点,避免了数据点集中在一个区域的问题。最后,利用直接最小二乘法进行椭圆参数拟合,得到式(2)中6个参数,并以Sampson误差作为判断依据获得一致性最好的椭圆参数。Sampson误差是一种点到圆锥曲线几何距离的近似,具有计算简单的优点,根据文献[19],其表示形式如下:
(9)
4 仿真试验与结果讨论
4.1 试验设计与初值设置
利用合成的目标航天器图像和真实的目标航天器图像进行试验。本章进行了3个试验,分别为:1)参数分析试验,为了分析边界点检测直线长度对算法性能的影响,在合成图像中,提取对接环外环椭圆,以提取椭圆的参数精度和提取时间为评价指标,设置不同的边界点检测直线长度进行试验。2)噪声试验,为了验证算法对噪声的鲁棒性,在合成图像中,提取对接环外环椭圆,以提取椭圆的参数精度为评价指标,利用包含噪声的合成图像进行试验。3)对比试验,以提取椭圆的正确性和提取时间为评价指标,真实图像中,将本文算法与Velasquez等[8]和Pătrăucean等[11]的方法进行对比。算法由Matlab编写,在安装有Windows 10系统的PC机(I5-480M@2.66GHz,8GB RAM)上运行。
利用合成图像进行试验时,设当前时刻两航天器的相对位置为tk=[200 mm,200 mm,5000 mm]T,相对姿态角为ak=[25°,20°,15°],计算时需将ak变换为相对姿态矩阵Rk。上一时刻两航天器的相对位置为tk-1=[190 mm,190 mm,4900 mm]T,相对姿态角为ak-1=[24°,19°,14°],计算时需将ak-1变换为相对姿态矩阵Rk-1。目标对接环外环尺寸为r=300 mm,相机镜头焦距f=25 mm,图像主点位置u0和v0同为512 pixel,像元尺寸μ=0.012 mm/pixel。合成图像中的目标如图2所示。
4.2 参数分析试验
令边界点检测直线数量m=40,验证不同边界检测直线长度γ对算法精度的影响,令γ依次为2,3,…,50 pixel,椭圆参数的真值由当前时刻对接环几何模型在图像中的投影获得,试验结果如图3~6所示。
试验结果表明,当γ<5 pixel时,多数边界点检测直线未穿过图像中对接环外环边界,参与椭圆拟合的数据点过少,得到的椭圆参数误差较大。当γ=5~40 pixel时,边界点检测直线全部穿过了图像中对接环外环边界,参与椭圆拟合的数据点数量总体稳定,得到的椭圆参数误差变化不大。当γ>40 pixel时,部分直线同时穿过了对接环外环和内环的边界,参与椭圆拟合的数据点数量开始下降,使误差开始增大。椭圆提取时间随着γ值的增大有增大的趋势。
4.3 噪声试验
由于空间拍摄的图像中存在噪声,这些噪声可认为是高斯噪声。为了验证算法对噪声的鲁棒性,分别在图像中增加4%,12%和20%的高斯噪声,在未对图像进行去噪处理的情况下,利用提出的算法提取目标椭圆,结果如表1所示。
从表1可以看出,对于存在噪声的图像,本文所提算法仍能较准确地提取出目标椭圆。因此,本文提出的算法对噪声具有一定的鲁棒性。
4.4 对比试验
利用真实图像进行对比试验,结果如图7~9所示,提出的方法能较准确地提取出对接环外环处的椭圆特征,Velasquez等[8]和Pătrăucean等[11]的方法提取出了较多错误的椭圆特征。在检测时间上,三种算法的检测时间分别为2290 ms,2920 ms和96 ms,因此,本文提出的方法优于另外两种方法。
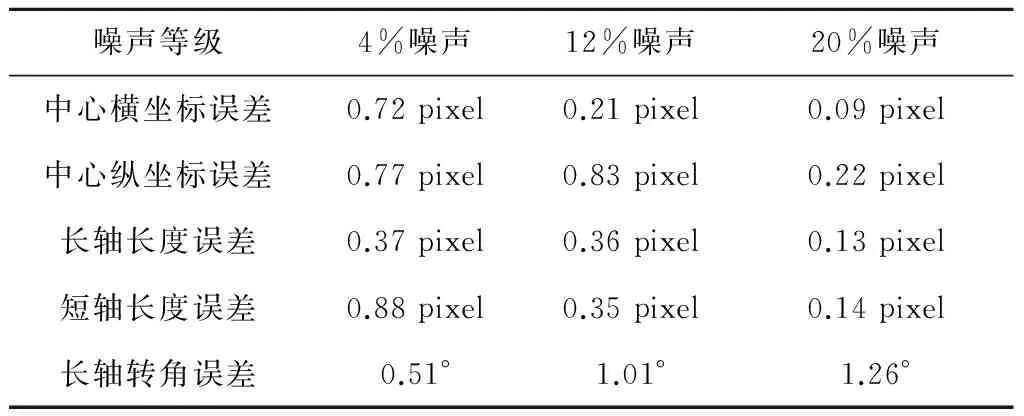
表1 不同等级的高斯噪声下提取的目标椭圆误差Table 1 Error of ellipse under different noise level
5 结 论
本文提出了一种非合作航天器上椭圆特征的提取方法。该方法通过检测图像中对接环附近的纹理边界点,去除粗大误差点后,采用直接最小二乘法得到椭圆的参数。利用合成图像和真实图像开展了仿真试验。结果表明,过长或过短的边界点检测直线都会影响算法的精度。在对比试验中,所提算法能够快速准确地提取目标航天器上的椭圆特征,性能好于两种对比算法。此外,本文所提算法对图像噪声具有一定的鲁棒性。因此,本文所提算法为航天器上椭圆特征提取提供了一种新思路。
[1] 钱萍,王惠南. 基于三目视觉测量的航天器交会对接相对位姿确定算法[J]. 宇航学报, 2010, 31(6):1575-1581. [Qian Ping, Wang Hui-nan. A trinocular vision measurement based relative attitude and position determination algorithm for RVD between spacecraft [J]. Journal of Astronautics, 2010, 31(6): 1575-1581.]
[2] 谷蔷薇,张世杰,曾占魁,等. 面向在轨服务的相对位姿单目视觉确定的凸松弛优化方法[J]. 宇航学报, 2016, 37(6):744-752. [Gu Qiang-wei, Zhang Shi-jie, Zeng Zhan-kui, et al. A convex relaxation optimization method of on-orbit servicing [J]. Journal of Astronautics, 2016, 37(6): 744-752.]
[3] 徐文福,梁斌,李成,等. 基于立体视觉的航天器相对位姿测量方法与仿真研究[J]. 宇航学报, 2009, 30(4):1421-1428. [Xu Wen-fu, Liang Bin, Li cheng, et al. The approach and simulation study of the relative pose measurement between spacecrafts based on stereo vision [J]. Journal of Astronautics, 2009, 30(4): 1421-1428.]
[4] 张庆君,胡修林,叶斌,等. 基于双目视觉的航天器间相对位置和姿态的测量方法[J]. 宇航学报, 2008, 29(1):156-161. [Zhang Qing-jun, Hu Xiu-lin, Ye Bin, et al. Binocular vision-based relative position and attitude determination between spacecrafts [J]. Journal of Astronautics, 2008, 29(1): 156-161.]
[5] 江刚武,龚辉,王净,等. 空间飞行器交会对接相对位置和姿态的在轨自检校光学成像测量算法[J]. 宇航学报, 2007, 28(1):15-21. [Jiang Gang-wu, Gong Hui, Wang Jing, et al. The optical measurement of self-calibration in orbit for spacecraft rendezvous and docking [J]. Journal of Astronautics, 2007, 28(1): 15-21.]
[6] Ma S D. Conics-based stereo, motion estimation, and pose determination [J]. International Journal of Computer Vision , 1993, 10 (1): 7-25.
[7] Xu W F, Xue Q, Liu H, et al. A pose measurement method of a non-cooperative GEO spacecraft based on stereo vision[C]. The 12th International Conference on Control Automation Robotics & Vision, Guangzhou, China, December 5-7, 2012.
[8] Velasquez A F, Luckett J, Napolitano M R, et al.Experimental evaluation of a machine vision based pose estimation system for autonomous capture of satellites with interface rings[C]. AIAA Guidance, Navigation, and Control Conference, Boston, USA, August 19-22, 2013.
[9] Lu C, Hu W. Effective method for ellipse extraction and integration for spacecraft images [J]. Optical Engineering , 2013, 52 (5): 1-18.
[10] Fitzgibbon A,Pilu M, Fisher R B. Direct least square fitting of ellipses [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21 (5): 476-480.
[11] Pătrăucean V, Gurdjos P, Von G R G. A parameterless line segment and elliptical arc detector with enhanced ellipse fitting[C]. The 12th European Conference on Computer Vision, Florence, Italy, October 7-13, 2012.
[12] Cai J, Huang P, Chen L, et al. An efficient circle detector not relying on edge detection [J]. Advances in Space Research , 2016, 57 (11): 2359-2375.
[13] Pătrăucean V. Detection and identification of elliptical structure arrangements in images: theory and algorithms[D]. Toulouse: Académie Technique Militaire,2012.
[14] 刘晓民. 纹理研究及其应用综述[J]. 测控技术, 2008, 27(5):4-9. [Liu Xiao-min. Summary of texture reseaarch [J]. Measurement & Control Technology, 2008, 27(5): 4-9.]
[15] Kaur A, Jindal G. Texturebased image segmentation using gabor filters [J]. International Journal of Engineering Science & Advanced Technology , 2014, 2 (3): 687-689.
[16] Kumar K N, Rao K S, Srinivas Y. Texturesegmentation based on multivariate generalized gaussian mixture model [J]. CMES: Computer Modeling in Engineering & Sciences , 2015, 107 (3): 201-221.
[17] Hua B O,Ma F L, Jiao L C. Research on computation of GLCM of image texture [J]. Acta Electronica Sinica , 2006, 1 (1): 155-158.
[18] Shahrokni A, Drummond T, Fua P. Texture boundary detection for real-time tracking[C]. The 8th European Conference on Computer Vision, Prague, Czech Republic, May 11-14, 2004.
[19] 昊福朝.计算机视觉中的数学方法[M].北京:科学出版社,2008:380-382.

