思维发展的核心:找到关联,构建系统
高中咏
数学知识间存在着内在联系。教师在教学中如果能够有效地沟通知识间的联系,学生就可能从整体上认识数学,形成知识链条,经历思维过程,体会到数学的有序有理,从而越学越清晰,越学越轻松。这是思维发展的核心,也是原汁数学的本质所在。本文以“图形的放大與缩小”一课为例,谈谈如何让数学课“原汁原味”。
一、思维的起始点:打破原有的平衡
案例1:教师出示一张A3纸与一张A4纸,并将A3纸对折,刚好与A4纸一样大
师:同学们,A3纸的面积刚好是A4纸面积的2倍,昨天老师拿着一张A3大小的建筑图纸到文印店,想把它复印并缩小为A4纸张的大小。
生:就是把图纸缩小到原来的1/2。
师:对!文印店的老板听了我的要求,把A3图纸放入复印机,先按下“缩小”按钮,再选择“缩小到50%”。同学们,你觉得复印的图纸会是我想要的那样吗?(学生点头赞同)
师:可是,出来的图纸却不是我想要的那样。
教师出示复印后的图,只有A4纸面积的一半那么大。
生1:怎么只有这么大?不可能!
生2: 50%就是1/2,怎么变了?
生3:是不是复印机坏了?(学生纷纷猜测原因)
师:其实,复印机并没有坏,这里面蕴含着一个数学知识。那就是我们今天学习的内容“图形的放大与缩小”(板书课题)
亚里士多德曾经说过:“思维自疑问和惊奇开始!”教师在课始巧妙创设“复印文件”的情境,这一素材既真实又新奇:与学生已有的知识经验产生矛盾,学生迫切地想知道“为什么50%不是1/2”,有效地唤起学生的好奇心和求知欲。
选择身边的材料引发学生积极思考,可以培养学生用数学的眼光看生活中的现象,逐步养成发现、研讨数学问题的习惯,这是数学学习的原动力和核心能力。
二、思维的生长线:寻找矛盾的根源
案例2:出示学习单,学生根据学习单自学课本学习单
1. 图形放大(或缩小),指的是把图形的( )放大或缩小。
2. 为什么图纸“缩小到50%”,不是原来的一半?你找到答案了吗?
3. 图形放大或缩小后,与原图形相比,什么变了,什么没变?
学生迫不及待地翻开课本,自学起来,继而开始汇报交流。
生1:图形的放大(或缩小),指的是把图形的每条边都放大或缩小。
生2:我知道为什么图纸的大小不是原图的一半了。缩小50%,指的是把图形的每条边缩小到原来的50%,不是把面积缩小到原来的50%。
师:那么,面积是怎样变化的呢?
生:面积应该只有原图形的1/4那么大。
师:为什么?
生:把一个长方形的图纸缩小50%,是把它的长和宽都缩小到原来的50%,面积就只有原来的50%×50%=25%。
师:同学们,你们很了不起,自己找到图纸大小不对的原因。把图纸“缩小到50%”,用我们今天的知识,应该怎样说?
生1:把图纸按2∶1缩小。
生2:把图纸按1∶2缩小。
师:把图形按一定的比放大(或缩小),指的是:变化后的图形与原图形之间的关系。比的前项和后项,表示的意义是一定的。
生1:比的前项表示变化后的图形,比的后项表示原图形。
生2:前项小就表示把原图形缩小,前项大就表示放大。
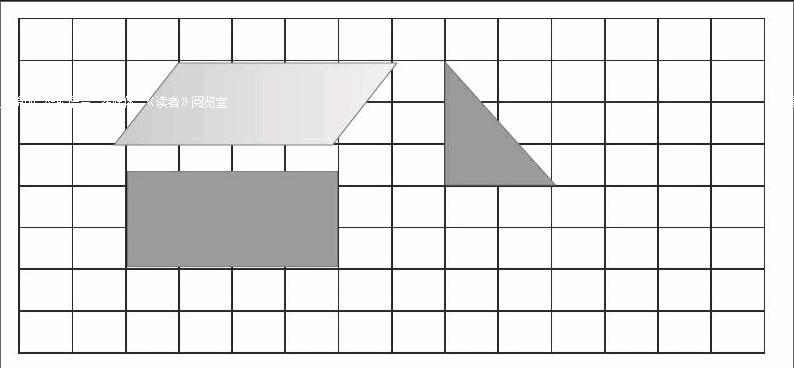
师:请同学们在方格纸上将下面各图形按1∶2缩小。
生1:我发现了,长方形的面积只有原图形面积的1/4,所以老师复印的图纸肯定只有原来图纸的1/4。
生2:不仅是长方形面积是原图形的1/4,平行四边形和三角形的面积都只有原图形的1/4。
生3:因为平行四边形和三角形的底、高只有原来的1/2,所以面积只有原来的1/4。
师:同学们都很有分析能力,我们再来看看图形放大或缩小后,与原图形之间什么会发生变化,什么没有变化?
生1:图形的每条边都会发生变化。
生2:周长和面积也会发生变化。好像都发生了变化,没有什么不变的。
生3:图形的样子没有变,只是大小变了。
生4:图形中角的大小没有变。
师:图形的样子没有变,我们叫形状不变。那为什么图形的形状不会变呢?
生:每条边都是同时变化的。
师:老师想要把图纸面积缩小到原来的一半,文印店老板应该按“缩小到百分之几” 的按钮呢?
生1:不能按50%了,应该比50%大,因为50%得到的只有1/4。
生2:应该是缩小到原来的70%,因为70%×70%=49%≈50%。
生3:对!如果是71%,它就大于50%了,因为71%×71%=50.41%。
师:同学们真厉害!我们放学后,就把你的方法告诉文印店的老板。
教师的作用不是告诉学生答案,而是引导学生探寻,激发学生思维。学生在矛盾冲突的驱使和学习单的引领下,通过自学,自主寻找到“缩小到50%不是一半”的原因所在,从总体上认清“图形的放大与缩小”的本质:是对应线段长度的比,不是面积的比,并且和以前学习的知识进行有效的沟通、联系和统一,使学生经历从矛盾、疑惑到清晰的过程,在学习中体会到数学的严密有理和数学魅力。
数学的根本就是发展思维。本环节中,教师在学生充分理解“图形的放大与缩小”的本质后,让他们尝试解决“复印图纸”的问题。这既是一种逆向思维的应用,又是数感的培养;既是知识的应用,更能体会数学思考的魅力。
三、思维的结构图:建立新的平衡
案例3:梳理知识,建立体系
师:通过本节课的学习,你有什么收获?
生1:我知道了:图形的放大或缩小,是指把图形的每条边都按一定的比进行放大或缩小。
生2:我知道了,图形放大或缩小后,图形的大小会发生变化,但形状不变。
生3:图形按一定的比放大或缩小,这个比的前项是变化后的图形。
师:通过今天的学习,让你想到过去学习的哪些知识?
生1:我想到了比和比例。
生2:我想到了图形的边扩大a倍,面积就会扩大到它的a2倍。
师:如果将一个长方体的模型按3∶1放大,放大后的长方体体积应该是原体积的多少倍?
生:放大后的长方体体积应是原体积的3×3×3=27倍,这是因为:放大是指把长、宽、高都放大到原来的3倍。
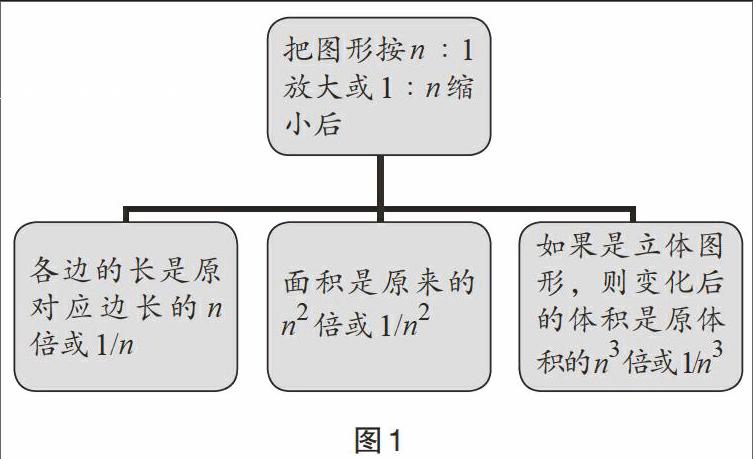
根据学生的回答,可以引导得出图1。
数学学习就是不断地打破旧的平衡,建立新的平衡。在这样的学习过程中,教师可以不断地完善学生的知识结构。学生在认识“图形的放大与缩小”的过程中,会从线段的关系认识到面积的关系,再上升到体积的关系,获得系统、合理的知识结构,形成多维的知识模块,建立上位的数学模型。
通过有效的问题情境,激活大脑,“勾住”旧知和经验,在矛盾冲突下经历抽象、推理、转化的过程,进行系统化思考,获得新的平衡,体现原汁数学的特征:从数学本质出发,学真数学,做真思考。
(作者单位:湖北武穴市师范附属小学)
责任编辑:孙建辉
zgjssjh@126.comendprint

