动物飞行的空气动力学

孙 茂(北京航空航天大学 流体力学研究所, 北京 100191)

0 引 言

动物飞行的流体力学是研究动物外部表面在流体中运动时产生的气动力或水动力的规律。

昆虫、鸟和兽(蝙蝠)的飞行是由作用于其上的气动力所决定的。匀速飞行时，作用于动物的气动力决定了其运动速度和所需的能耗；运动受到扰动时或动物希望作机动运动时，气动力随时间的变化特性决定了运动的稳定性和机动性。运动速度的快慢、运动效率和持久性以及运动的机动性与攫取食物、逃避敌害、追求配偶等生存需要密切相关。因而，了解动物外部表面产生气动力的机制和规律，是研究相关动物的比较生理学、行为学、生态学及进化的基础。这些机制和规律也可为发展新型飞行器提供仿生学指导。

在过去的20余年中，由于生物学和流体力学工作者的合作，实验和计算条件的提高，及发展仿生微型飞行器需求的推动，动物飞行的流体力学研究领域有了很大的进展。我们在这里介绍一些重要工作，并讨论该领域的未来发展趋势和需要进行的工作。

1 昆虫的飞行

先简介昆虫翅膀的拍动运动。大多数昆虫的翅膀近似在一个称为拍动平面的平面内拍动 (图 1)。对于某一昆虫，拍动平面与身体的夹角通常是固定的。若将昆虫翅膀近似为一刚性板，则翅膀的拍动运动(翅膀相对于身体的运动)可用三个欧拉角来描述：

方位角φ、抬升角θ和(几何)攻角ψ(或α)(图1)。方位角φ的变化幅度称为拍动幅度(Φ)；对于不同的昆虫，Φ约在60°～180°之间, 大多数在120°左右[1-3]。对于大多数昆虫，抬升角θ较小，小于10°[1,4-5]，这就是为什么上面说“昆虫翅近似在一个平面内拍动”的原因(果蝇是一个例外，其抬升角较大，大于30°[2])。攻角α通常约为35°或更大[1,4-5]。不同昆虫的拍动频率(n)约在25～400 Hz之间[6]。昆虫翅不是刚性的，拍动中翅膀会产生偏离刚性板的变形。对于尺寸小的昆虫，这种变形很小，例如果蝇，变形几乎没有[7]；只有较大的昆虫，例如蝴蝶，变形才比较大[6]。

图1 描述翅膀拍动运动的各个角度Fig.1 Angles of a flapping wing that determine the wing orientation

早期(20世纪70～80年代)有关昆虫飞行气动力的研究思路类似于直升机旋翼和飞机螺旋桨的研究思路：通过对昆虫翅膀运动进行观察，获得拍动频率、拍动角等参数，从而得知翅膀的运动速度；将翅膀置于风洞定常来流中，在相应的雷诺数(Re)下测量气动性能数据(升、阻力系数，CL和CD，随攻角的变化关系)；然后利用“叶素理论”和“动量理论”，基于测得的气动性能数据及翅膀在每一时刻的速度和攻角，估算昆虫飞行的升力和能耗。这一思路的基本假设是拍动翅的气动力是准定常的。结果表明，上述定常条件下测到的升力系数远不能给出平衡昆虫重量的升力，说明不能用定常流理论来解释昆虫的飞行[8]。例如，图2为果蝇翅在定常流动条件下升、阻力的极曲线：即使在攻角为30°时，CL也很小，只有0.6，远小于昆虫需要用来平衡重量的升力系数，2左右[9](此升力系数比飞机巡航飞行的升力系数大约三倍；这是因为，昆虫翅膀尺寸小故拍动时与空气的相对速度小，故需要的升力系数大，故称为高升力)。在同一时期，Weis-Fogh(生物学家)在研究台湾小黄蜂的飞行时发现，该昆虫在每一次下拍前，两翅会在背部“合拢”，然后快速“打开”[10]。Lighhill[11]和Maxwoothy[12]分别对翅膀的“合拢打开”进行了理论分析和实验，表明这一运动可产生很大的非定常升力；人们称此高升力机制为Weis-Fogh机制。虽然大多数昆虫不作打开合拢运动，但是Weis-Fogh机制的发现和上述对准定常假设的否定，促使人们从流动的非定常方面去思考昆虫产生高升力的问题。

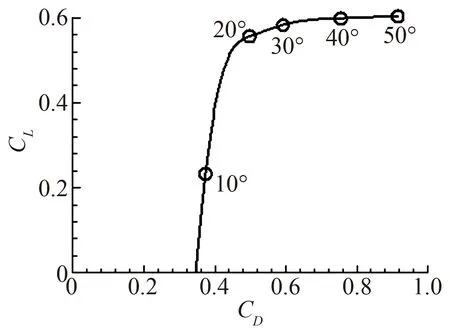
图2 果蝇翅在定常流动条件下升、阻力的极曲线Fig.2 Lift and drag coefficients of a fruit-fly wing under steady-state condition

如果说，以上工作的主要结果是否定了昆虫用定常流模式产生升力这一想法，那么，进入90年代，人们开始具体研究昆虫的非定常流动过程与其中的机理。由于每一次拍动都是在大攻角下的快速加速后和之后的平动，人们认为昆虫可能是利用动态失速机制，即保持瞬态高升力的机制，来产生足够的升力的。Dickinson及其合作者[13]测量了翼型启动后的升力(Re=75～225，针对果蝇等昆虫)，结果表明的确有大升力，但其只能维持翼型运动约2个弦长所需的时间(Re数较大时，该时间较长些。例如，Re=1000时，约为运动3个弦长的时间)。一般地，昆虫翅膀拍动时，翅膀外部的翼剖面要运动约4个弦长(而在前飞速度较大时，将为约7个弦长)。因而，人们又想，也许动态失速并不在这里起重要作用。到1996年，Ellington等[14]通过对鹰蛾飞行及其翅膀的自动拍动模型的流动显示，观察到拍动翅膀上的失速涡在整个平动过程中都不脱落，原因是存在一展向流动，其稳定了失速涡(Ellington称之为“前缘涡”，见图3)。这就是说，动态失速的高升力可在平动过程中得以保持。这是一重大发现，称为“不失速机制”。这一结果被以后的实验和数值计算所证实。

图3 模型鹰蛾翅拍动运动时的前缘涡Fig.3 LEV on a flapping model hawkmoth wing

上述工作表明上、下拍过程中，不失速机制可产生高升力。还有些其他高升力机制吗？翅膀在下拍至上拍之间(或下拍至上拍之间)存在一翻转运动，在上拍(或下拍)的开始为一启动加速运动。Dickinson小组[15]的实验和孙茂小组[16]的数值计算及涡动力的分析表明，拍动开始的加速运动，由于附加质量的作用，可产生大升力；拍动结束阶段的快速上仰运动也可产生大升力。此二个升力机制分别称为“快速加速机制”和“快速上仰机制”。但应指出，虽然三个机制均起作用，但因不失速机制作用的时间较长，且在其作用时翅膀运动的速度较大，故该机制产生的气动力占整个拍动周期中的大部分[2,9,17]，即不失速机制是产生高升力的主要机制。

对昆虫拍动翅产生高升力的机理有了一定认识之后，人们希望有对拍动翼气动力的简单估算方法；简单方法由于抓住了问题的主要因素，还可对问题的物理机制有进一步的认识。童秉纲小组[18]基于模型理论分析途径发展了二维拍动翼的半解析方法，上述三个升力机制均能在该方法中体现。Dickinson小组[19]将准定常理论中的升、阻力系数用转动翼的取代，得到简单的升、阻力计算公式；该方法虽不能正确计算快速加速和快速上仰二个机制产升的升力，但还是能正确计算拍动翅升、阻力的主要部分；这是因为转动翼的流动包含了不失速机制这一产生高升力的主要机制。

昆虫翅膀具有褶皱，且在拍动中会变形。上述高升力机制的研究是用平板翼模型来进行计算或实验的，变形和褶皱会不会导致新的气动力机制，是人们很关心的问题。Taylor研究小组[20]用四台高分辨率的摄像机测出了自由悬停飞行的食蚜蝇翅膀变形的时间过程(变形主要为沿展向的扭转和沿弦向的弯曲)。杜刚和孙茂[21]用此测量数据，并加上褶皱(食蚜蝇等昆虫翅的褶皱数据已存在)，用变形运动网格进行数值模拟，结果表明：对于悬停飞行的情形，单独变形的影响是使升力增大，能耗减小；单独褶的影响是恰好相反；褶皱和变形同时存在(这是实际情况)时，两者的影响会相互抵消而变得很小。因而，褶皱的作用主要是结构上的而非气动上的；平板翼可很好地近似真实翼(平板翼的攻角取为真实翼面积二阶矩折合半径处的攻角)。

虽然大部分昆虫在功能上可视为只有一对翅膀，有的昆虫(如蜻蜓)功能上却有两对翅膀。前、后翅气动干扰如何，有否新的高升力机制，是十分有趣的问题。孙茂小组[22]和Isogai小组[23]分别用计算和实验的方法研究了悬停飞行的蜻蜓前后翼的干扰问题，表明了当前翼滞后于后翼拍动时(蜻蜓和豆娘的拍动都是如此)，两翼的干扰是不利的，但十分小。但对于滑翔飞行(蜻蜓是少有的能滑翔的昆虫之一)，陆夕云小组[24]的研究表明前后翅存在有利且较大的干扰。

前面说到，不失速机制是产生高升力的主要机制。以前研究过的蝇、蜂、蛾等昆虫，气动力主要是由不失速机制产生的。也就是说，是由翅膀携带着 LEV 运动而产生的。这需要翅膀运动一段路程，即拍动幅度要足够大。若拍动幅度很小，比如蚊子只有约40°，食蚜蝇只有约60°，则翅膀刚完成启动阶段的加速，便要开始减速了。这样的话，LEV 还没有发展起来，拍动就进入结束阶段了，也就无法利用不失速机制了；也就是说，与许多其它昆虫不同，蚊子和食蚜蝇度拍动幅度小的昆虫可能不是利用不失速机制产生高升力的。最近的工作[25-26]表明了这一点:它们是用“划桨”机制产生高升力的。“划桨”机制是通过在短时间内在翅膀的前缘和后缘产生不同方向的新涡量来产生大升力的[26], 不像不失速机制那样, 是通过两个涡(LEV和启动涡)的相对运动来产生大升力(图4)。

图4 左边，“划桨”机制在翅膀的前缘和后缘产生不同方向的新涡量；右边，不失速机制两个涡(LEV和启动涡)的相对运动Fig.4 Left, vortex wake in the “paddling” mechanism; right, vortex wake in the delayed-stall mechanism

另外，对于极端小的昆虫(翅长小于1 mm)，雷诺数十分小，约为10。这时黏性效应很大，LEV十分弱，也不能用不失速机制产生高升力[27-28]。所需的高升力如何产生，还是未解决的问题。

以上工作和进展主要是针对悬停飞行的；可以说人们对于悬停飞行的，气动力机制和规律已有了较好了解。对于前飞和其它飞行状态的气动力规律还几乎没有什么研究。首先，这些飞行状态的翅膀拍动运动(包括翅的变形)需要细致的观测数据；这一工作将比悬停飞行或悬停附近的机动飞行的情形困难很多。有了翅膀的拍动运动和变形数据，气动力特性可通过模型实验和Navier-Stokes方程的数值求解进行研究。Ellington 小组[29-30]早年对熊蜂和蝇蛾的前飞作了观测，但速度范围较小，且由于当时实验设备条件限制，有的数据(如翅膀攻角)不能测到。最近，用较先进的观测系统和专门研制的风洞，孙茂小组给出了较完整的蜂蝇前飞的拍动数据[31]。但气动力机制和规律尚有待研究。

2 鸟类的飞行

鸟类飞行时产生升力以托举其重量，产生推力以克服身体各部分阻力。可能是因为鸟的尺寸较大从而翅膀运动雷诺数较大(Re=1×103～1×105)及拍动频率较低，人们一般认为鸟产生升力的机制与飞机类似，即鸟翼是用传统的空气动力学原理产生升力和阻力的(这里“传统空气动力学”指定常、附着流的空气动力学)。这样，广泛用于飞机机翼、直升机旋翼和飞机螺旋桨的，基于叶素理论和动量定理的准定常方法，就可以用来计算鸟类的升力、阻力和能耗了。这些观点反映在早期的一些专著中(例如文献[32-33])。反过来说，如果用叶素理论和动量定理计算出的升力能平衡鸟的重量，也就从一个侧面证明了上述有关鸟类用传统空气动力学原理产生气动力的猜想。但是，要利用叶素理论，需要知道鸟翼每一剖面任一时刻的运动速度和攻角，以及剖面的升、阻力系数随攻角的变化关系。获得这些数据是十分困难的(测量鸟翼拍动时的形态学和运动学参数比测量昆虫的这些参数困难得多)。因而，人们并没有系统地进行这方面的工作。早期的研究主要是用简单的力学原理估算气动力和能耗[32]：升力等于重量(可测得)；推力等于身体各部分阻力，其正比于V2(V为飞行速度)；产生升力所需的功率(称为诱导功率)，用动量定理计算，其正比于1/V(应用动量定理时假设鸟翼扫过的面积为一圆面)。从而可知，飞行的需用功率由二部分组成：克服身体各部分阻力的功率，正比于V3；诱导功率，正比于1/V。这表明飞行速度较小或较大时，功率较大，而在某一中等速度下，功率最小，即功率随飞行速度的变化关系呈一“U”形曲线(飞机和直升机亦如此)。

上面应用动量定理的计算中将鸟翼的作用视为一圆形作用面，以常速(诱导速度)下排空气；这是对鸟翼与周围空气相互作用的一个很大的简化。人们试图知道鸟翼究竟是怎样与周围的空气相互作用而产生气动力的。鸟飞行时留下的尾迹是鸟翼与空气相互作用的结果；对尾迹的流动显示和定量测量也相对容易一些。因而人们开始通过研究鸟的尾迹来推知和估算翼上的气动力。

最早的这类研究是Rayner[34-35]的尾涡理论模型，其对拍动运动作一些假设后，基于涡动力学理论认为，翼每次下拍产生一标准的圆形涡环(上拍无作用)，尾迹由涡环串组成。给定鸟的重量，平均升力就确定了，从而涡环的强度和运动可确定，进而诱导功率可确定。当时的(较粗略的)流动显示实验也表明了尾迹中有环状涡结构[36]。这一模型比动量定理的圆盘作用面模型更真实地反映了鸟翼与流体的相互作用，可更好地计算诱导功率。但其对尾迹和拍动运动都作了较大的简化假设；之后的许多流动显示实验都表明了这一点[37-38]。

随着流场速度测量方法的发展，人们开始用PIV方法定量测量鸟类尾迹的速度场，从而可计算出涡量场；还建造了专门的风洞(Lund University Wind-Tunnel)[39]，并发展了新的训练鸟在风洞中飞行的方法[38]。Spedding等[38]系统地测量了一种夜莺在不同飞行速度下飞行的尾迹速度场(离鸟约15个弦长之后的远场尾迹)，从而获得尾涡结构和强度(见图5)。结果表明：飞行速度较低时，远场尾迹主要由一对对的涡环组成，下拍产生一直径较大、环量较大的涡环(非标准圆形)，上拍产生一较小和较弱的涡环。飞行速度较大时，尾迹主要由两个分别发自左右翼尖的尾涡(流向涡)和连接它们的若干展向涡构成(形状犹如梯子)；两尾涡的环量沿其涡轴线周期性变化，两尾涡的间距和两尾涡在垂直方向的位置也周期性地变化。在较小和较大速度之间，随着速度的增加，尾迹从前者逐渐过渡到后者。用测得的涡的环量，涡的几何形状和方位，可近似估算出翼上拍的平均气动力和下拍的平均气动力分别是多少。估算出的升力能近似平衡鸟的重量。这一工作的意义在于，它能告诉人们气动力是上拍还是下拍产生的，各产生多少，升力和阻力分别是多少。

图5 一种夜莺飞行时身体对称面内尾迹的速度场和涡量场Fig.5 Velocity and vorticity field

接着，同一研究小组对形态和运动上各异的若干鸟类做了类似的实验研究，包括知更鸟[40]、雨燕[41-42]、黑顶莺[43]、斑鹟[44]等。不同的鸟或者同一鸟在不同飞行速度下，尾涡结构不同，但都与上述夜莺的某一种尾涡结构大体上相似。

到目前为止的尾迹测量能近似给出上拍或下拍的平均气动力，有时甚至可近似给出瞬时气动力[43-44]。但是由于没有翼面附近的流场信息，这些工作不能解释气动力是如何产生的。在文献[44]中，斑鹟的瞬时气动力合力系数最大可达2.7，如此大的力系数是不能用传统的空气动力学原理解释的，其产生的机理十分值得研究。今后的工作应着眼于翅膀拍动运动中形态学和运动学参数的细致测量，及翼面附近的流场、翼面压强和翼的气动力的测量和(或)计算，这样才能揭示鸟翼产生升力和推力的机理。

上面有关鸟类飞行的研究简介，没有包括蜂鸟。与其它鸟不同，蜂鸟的拍动运动方式更像昆虫，上拍时可将翅膀翻转过来(翅背部作下翼面，底部作上翼面)，产生与下拍同量级的气动力(其它鸟的上拍中，通常翅膀面积变小，攻角近似为0°，产生很小的气动力或几乎不产生气动力)。因为可使蜂鸟在实验室条件下长时间悬停，对其流场的测量也更详尽些，有尾迹的结果[45]，也有一些翼面附近的流场的结果[46]。尾迹流场(从而涡量场)的测量结果给出了上拍和下拍分别产生的平均气动力[45]。翼面附近的测量的结果[46]表明翅上存在前缘涡，流动不是附着的。这表明蜂鸟有可能是用与昆虫类似的机制产生气动力，但这需要进一步的工作来证实，特别是需要翅膀气动力、翼面压力分布和翼附近的流场的测量和计算方面的工作。有关蜂鸟前飞的工作还没有开展。

3 蝙蝠(兽类)的飞行

蝙蝠是唯一能飞行的哺乳动物，与鸟类同为能飞行的脊椎动物。蝙蝠进化到飞行的途径与鸟类不同，但大多数蝙蝠在翅膀形态、拍动方式和飞行速度上与相同尺寸的鸟略同，飞行的雷诺数也相当(Re=1×103～1×105)。因而，对两者飞行的空气动力学的研究也有许多共同之处。当然，蝙蝠和鸟也有一些重要差别，例如，鸟翅在上拍时可通过羽毛的转动而使翅膀形如百叶窗，从而使翅膀的阻力很小，而蝙蝠是通过折叠其翅膜来减小这种气动力的。

与鸟类一样，人们早期对蝙蝠飞行的研究主要基于传统的空气动力学原理(定常、附着流机翼理论；动量定理；叶素理论)来推算飞行的能耗、持久性、机动性等性能，以及这些性能与翅膀展弦比、翼载等参数的关系[33]。

前面讲到过，对于鸟类，除用简单力学原理估算飞行的能耗等外，对气动力机理的研究主要是通过测量和分析动物飞行时留下的尾迹来进行的。对于蝙蝠，情况也是如此，只是开始得比鸟类晚一些，但因利用了在对鸟类研究中取得的经验，很快就与鸟类研究同步了。在约1984～2006年期间，人们通过对鸟类飞行的尾迹的测量，对鸟类飞行的气动力产生的过程有了一定的了解。而从2006年开始，人们开始用相同的方法(用PIV方法测量尾迹的速度场，从而获得尾涡的环量，进而推算翅膀上的气动力)，研究蝙蝠的气动力特性。

布朗大学的Breuer小组[47]在8 m长(截面为1×2 m2)的“飞行长廊”中，测量了一种短鼻果蝠的尾迹和翅膀的主要运动参数。他们发现蝙蝠的尾迹比鸟类的更复杂，并且起动涡比鸟类的强得多(起动涡强表明拍动初期翅膀的攻角大且加速度大；这与运动学测量结果一致)。由于实验是在“飞行长廊”中进行的，蝙蝠只是在某个速度下飞行，而该速度的选择也可能不是自然的，因为蝙蝠可能受到长廊四壁的约束。

Hedenstrom 和 Spedding 的研究小组[48]在他们的专门风洞中(即上述用于鸟类飞行实验的Lund University Wind-tunnel)对一种体积较小的叶口蝠类的蝙蝠进行了实验，测量了低、中、高三种飞行速度(1.2～7.5 m/s)下的尾迹 (图 6为低速飞行时身体对称面内的尾迹速度场和涡量场)。实验结果表明，低速飞行时，上拍或下拍中，每一翅膀产生一个涡环，而不是像鸟那样，两个翅膀产生一个涡环。中等和高飞行速度时，下拍时，与鸟相同，尾迹主要由发自左、右翼尖的尾涡和连接它们的展向涡构成；而上拍时，翅膀的外部会产生一与低速飞行时类似的涡环，从而可推断，上拍时翅膀外部的环量与翅膀内部的方向相反。由尾迹的涡结构和环量，他们近似地推断出上、下拍的升力系数，并指出高飞行速度时的上拍过程中，蝙蝠通过翻转翅膀外部，产生一定的推力。从他们由尾迹推算出的气动力系数来看，翅膀升力系数较大，不能用传统空气动力学理论解释。从而他们推测，应有非定常机制在起作用。之后，他们又进行了测量翅膀附近绕流实验[49]：测量了帕拉斯长舌蝙蝠(三个个体)飞行时，下拍中部时刻的翅膀绕流，发现下拍过程中存在前缘涡，表明了蝙蝠用非定常机制产生气动力。应指出，由于PIV方法测速在物面附近误差较大，翅膀附近绕流的测量只能说是十分初步的结果。最近，Breuer 小组[50]和 Hedenstrom/Spedding小组[51]对另外几种蝙蝠的飞行进行了尾迹测量的实验。在这些实验中，他们在测量尾迹的同时，对翅膀拍动的运动学参数作了更细致的测量。

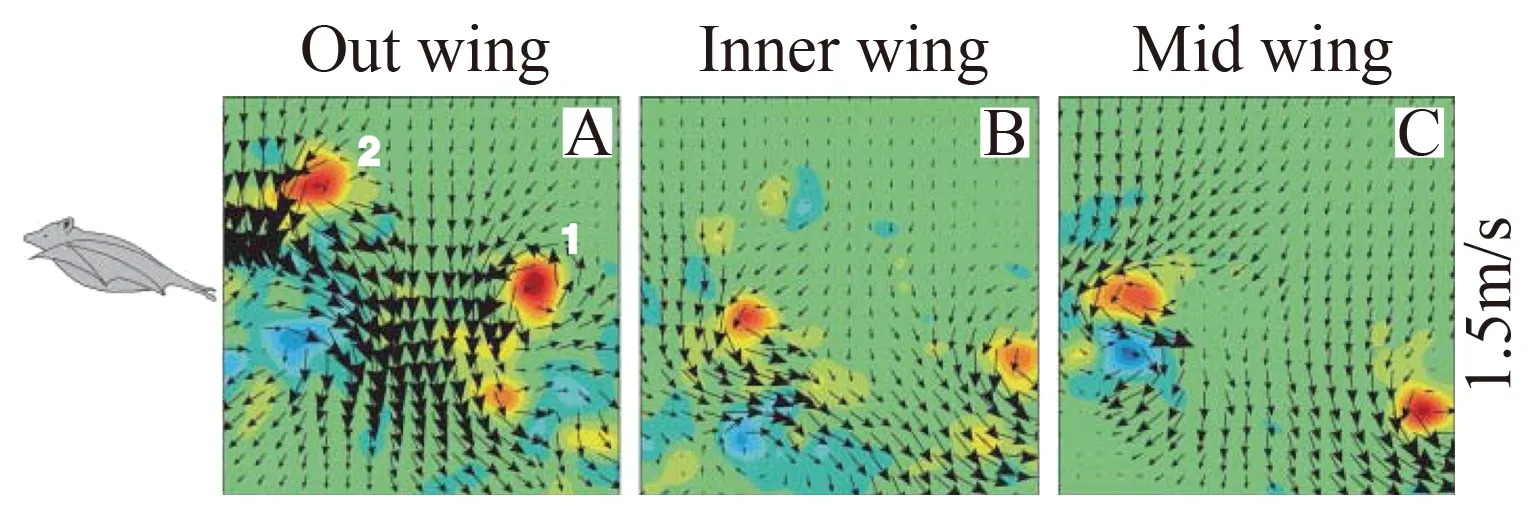
图6 叶口蝠低速(1.5 m/s)飞行时身体对称面内尾迹的速度场和涡量场Fig.6 Velocity and vorticity field

较早给出蝙蝠拍动翼附近的细致流场，并由此分析其中的高升力机理的是中国学者[52-56]。何国威小组通过数值模拟，率先给出了模型蝙蝠翼拍动中的细致流动结构(例如图7[54])。基于对流动结构、翼的运动和力的特性的分析，他们发现蝙蝠翼拍动中翼展的动态变化(周期性伸长和缩短)会使前缘涡增强，从而增大升力[52-54]。余永亮小组用面元法研究了蝙蝠翼拍动时变形对的空气动力特性的影响, 分别研究弓形变形、扭转变形及展向变形的作用，结果表明弓形变形可显著增大升力[55-56]。

图7 模型蝙蝠低速飞行中翼的前缘涡及翼尖涡(左，流线；右，涡量)[54]Fig.7 The streamlines and vortical structures around the bat wings

到现在为止，可以说对蝙蝠飞行的翅膀拍动运动的测量方面、流动机理研究方面, 已甚至超过了鸟类，但仍需进一步探索是否还有其它升力机制。

4 未来5～10年的研究工作

1) 昆虫前飞、爬升及垂直上飞时翅膀拍动运动学参数的细致测量。基于翅膀运动学数据的模型实验和N-S方程模拟，探讨上述飞行时可能存在的空气动力学新机理。

2) 极小昆虫(翅长小于1 mm，Re为10的量级)的飞行方式和气动力机制的研究：实验观测，发现新拍动方式；计算和理论分析揭示新气动力机理。

3) 鸟类典型飞行状态的翅膀拍动运动学参数的细致测量。基于鸟类翅膀运动学数据的模型实验和N-S方程模拟，探讨鸟类气动力的特性与其产生机理。

4) 蝙蝠典型飞行状态的翅膀拍动运动学参数的细致测量。基于运动学数据的模型实验和N-S方程模拟，进一步探讨蝙蝠气动力的特性与其产生机理。

[1]EllingtonC P. Aerodynamics of hovering insect flight. III： Kinematics[J]. Phil Trans R Soc Lond B, 1984, 305: 41-78

[2]FryS N, Sayaman R, Dickinson M H. The aerodynamics of hovering flight in Drosophila[J]. J Exp Biol, 2005, 208: 2303-2318

[3]Mou X L, Liu Y P, Sun M. Wing motion measurement and aerodynamics of hovering true hoverflies[J]. J Exp Biol, 2011, 214: 2832-2844

[4]LiuY P, Sun M. Wing kinematics measurement and aerodynamics of hovering drone-flies[J]. J Exp Biol, 2008, 211: 2014-2025

[5]Walker S M, Thomas A L R, Taylor G K. Deformable wing kinematics in free-flying hoverflies[J]. J R Soc Interface, 2010, 7: 131-142

[6]Dudley R. The biomechanics of insect flight: form, function, evolution[M]. Princeton: Princeton University Press, 2000

[7]Vogel S. Flight in drosophila. II: Variations in stroke parameters and wing contour[J]. J Exp Biol, 1967, 46: 383-392

[8]Ellington C P. The aerodynamics of hovering insect flight. Ⅰ: The quasi-steady analysis[J]. Phil Trans R Soc Lond B, 1984, 305: 1-15

[9]Sun M, Du G. Lift and power requirements of hovering insect flight[J]. Acta Mech Sinica, 2003, 19(5): 458-469

[10]Weis-Fogh T. Quick estimates of flight fitness in hovering animals, including novel mechanism for lift production[J]. J Exp Biol, 1973, 59: 169-230

[11]Lighthill M J. On the Weis-Fogh mechanism of lift generation[J]. J. Fluid Mech, 1973, 60: 1-17

[12]Maxworthy T. Experiments on the Weis-Fogh mechanism of lift generation by insects in hovering flight. Part 1: Dynamics of the fling[J]. J Fluid Mech, 1979, 93, 47-63

[13]Dickinson M H, Götz K G. Unsteady aerodynamic performance of model wings at low Reynolds numbers[J]. J Exp Biol, 1993, 174: 45-64

[14]Ellington C P, Van Den Berg C, Willmott A P, et al. Leading-edge vortices in insect flight[J]. Nature, 1996, 384: 626-630

[15]Dickinson M H, Lehman F O, Sane S P. Wing rotation and the aerodynamic basis of insect flight[J]. Science, 1999, 284: 1954-1960

[16]Sun M, Tang J. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion[J]. J Exp Biol, 2002, 205: 55-70

[17]Aono H, Liang F, Liu H. Near and far-field aerodynamics in insect hovering flight: An integrated computational study[J]. J Exp Biol, 2008, 211: 239-257

[18]Yu Y L, Tong B G, Ma H Y. An analytical approach to theoretical modeling of highly unsteady viscous flow excited by wing flapping in small insects[J]. Acta Mech Sinica, 2003, 19: 508-516

[19]Sane S P, Dickinson M H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight[J]. J Exp Biol, 2002, 205: 1087-1098

[20]Walker S M, Thomas A L R, Taylor G K. Deformable wing kinematics in free-flying hoverflies[J]. Journal of the Royal Society Interface, 2010, (7): 131-142

[21]Du G, Sun M. Aerodynamic effects of corrugation and deformation in flapping wings of hovering hoverflies[J]. J Theor Biol, 2012, 300(9): 19-28

[22]Sun M, Lan S L. A computational study of the aerodynamic forces and power requirements of dragonfly Aeschna juncea hovering[J]. J Exp Biol, 2004, 207: 1887-1901

[23]Yamamoto M, Isogai K. Measurement of unsteady aerodanamic forces for a mechanical dragofly model[J]. AIAA J, 2005, 43: 2475-2480

[24]Zhang J, Lu X Y. Aerodynamic performance due to forewing and hindwing interaction in gliding dragonfly flight[J]. Phys Rev E, 2009, 80: 017302

[25]Bomphrey R J, Nakata T, Phillips N, et al. Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight[J]. Nature, 2017, 344(7648): 92-95

[26]Zhu H J, Sun M. Unsteady aerodynamic force mechanisms of a hoverfly hovering with a short stroke-amplitude[J]. Physics of Fluids, 2017, 29: 081901 (1-10)

[27]Wu J H, Sun M. Unsteady aerodynamic forces of a flapping wing[J]. Journal of Experimental Biology, 2004, (207): 1137-1150

[28]Miller L A, Peskin C S. When vortices stick: An aerodynamic transition in tiny insect flight[J]. J Exp Biol, 2004, 207: 3073-3088

[29] Dudley R, Ellington C P. Mechanics of forward flight in bumblebees. I: Kinematics and morphology[J]. J Exp Biol, 1990, 148: 19-52

[30]Willmott A P, Ellington C P. The mechanics of flight in hawkmoth Manduca sexta. I: Kinematics of hovering and forward flight[J]. J Exp Biol, 1997, 200: 2705-2722[31]Meng X G, Sun M. Wing and body kinematics of forward flight in drone-flies[J]. Bioinspir Biomim, 2016, (11): 056002(1-19)

[32]Pennycuick C J. Animal flight[M]. London:Edward Arnold (Publishers) Limited, 1972[33]Norberg U M. Vertebrate flight[M]. Berlin, Heidelberg: Springer Verlag, 1990

[34]Rayner J M V. A vortex theory of animal flight. Part 1: The vortex wake of a hovering animal[J]. J Fluid Mech, 1979, 91: 697-730

[35]Rayner J M V. A vortex theory of animal flight. Part 2: The forward flight of birds[J]. J Fluid Mech, 1979, 91: 731-763

[36]Kokshaysky N V. Tracing the wake of a flying bird[J]. Nature, 1979, 279: 146-148

[37]Spedding G R, Rayner J M V, Pennycuick C J. Momentum and energy in the wake of a pigeon (Columba livia) in slow flight[J]. J Exp Biol, 1984, 111: 81-102

[38]Spedding G R, Rosen M, Hedenstrom A. A family of vortex wakes generated by a thrush nightingale in free flight in a wind tunnel over its entire natural range of flight speeds[J]. J Exp Biol, 2003, 206: 2313-2344

[39]Pennycuick C J, Alerstam T, Hedenstrom A. A new low-turbulence wind tunnel for bird flight experiments at Lund University, Sweden[J]. J Exp Biol, 1979, 200: 1441-1449

[40]Hedenstrom A, Rosen M, Spedding G R. Vortex wakes generated by robins Erithacus rubecula during free flight in a wind tunned[J]. J R Soc Interface, 2006, (3): 263-276

[41]Henningsson P, Spedding G R, Hedenstrom A. Vortex wake and flight kinematics of a swift in cruising flight in a wind tunne[J]. J Exp Biol, 2008, 211: 717-730

[42]Henningsson P, Muijres F T, Hedenstrom A. Time-resolved vortex wake of a common swift flying over a range of flight speeds[J]. J R Soc Interface, 2011, (8): 807-816

[43]Johansson L C, Hedenstrom A. The vortex wake of blackcaps (Sylvia atricapilla L.) measured using high-speed digital particle image velocimetry (DPIV)[J]. J Exp Biol, 2009, 212: 3365-3376

[44]Muijres F T, Bowlin M S, Johansson L C, et al. Vortex wake, downwash distribution, aerodynamic performance and wingbeat kinematics in slow-flying pied flycatchers[J]. J R Soc Interface, 2012, 9: 292-303

[45]Warrick D R, Tobalske B W, Powers D L. Aerodynamics of the hovering hummingbird[J]. Nature, 2005, 435: 1094-1097

[46]Warrick D R, Tobalske B W, Powers D L. Lift production in the hovering hummingbird[J]. Proc R Soc B, 2009, 276: 3747-3752

[47]Tian X D, Iriarte-Diaz J, Middleton K, et al. Direct measurements of the kinematics and dynamics of bat flight[R]. AIAA 2006-2865

[48]Hedenstrom A, Johansson L C, Wolf M, et al. Bat flight generates complex aerodynamic tracks[J]. Science, 2007, 316: 894-897

[49]Muijres F T, Johansson L C, Barfield R, et al. Leading-edge vortex improves lift in slow-flying bats[J]. Science, 2008, 319: 1250-1253

[50]Hubel T Y, Riskin D K, Swartz S M, et al. Wake structure and wing kinematics: the flight of the lesser dog-faced fruit bat, Cynopterus brachyotis[J]. J Exp Biol, 2010, 213: 3427-3440

[51]Muijres F T, Johansson C J, Winter Y, et al. Comparative aerodynamic performance of flapping flight in two bat species using time-resolved wake visualization[J]. J R Soc Interface, 2010, (8): 1418-1428

[52]Wang S Z, Zhang X, He G W, et al. Lift enhancement by dynamically changing wingspan in forward flapping flight[J]. Physics of Fluids, 2014, 26(6): 1-56

[53]Wang S Z, He G W, Zhang X. Lift enhancement on spanwise oscillating flat-plates in low-Reynolds-number flows[J]. Physics of Fluids, 2015, 27(6): 61901

[54]Wang S Z, Zhang X, He G W, et al. Lift enhancement by bats’ dynamically changing wingspan.s[J]. J R Soc Interface, 2012, 113(12): 20150812

[55]Yu Y, Guan Z. Learning from bat: Aerodynamics of actively morphing wing[J]. Theoretical and Applied Mechanics Letters, 2015, 5(1): 13-15

[56]Guan Z, Yu Y. Aerodynamic mechanism of forces generated by twisting model-wing in bat flapping flight[J]. Applied Mathematics and Mechanics, 2014, 35(12): 1607-1618.