尾缘襟翼缝隙大小对风力机翼型气动性能的影响
贾亚雷, 韩中合, 安 鹏, 李恒凡, 董 帅(. 华北电力大学 电站设备状态监测与控制教育部重点实验室, 河北 保定 07003;2. 河北软件职业技术学院, 河北 保定 07000)
0 引 言
国内外对风力机的气动载荷控制已经有了广泛的研究,包括变桨控制和智能叶片控制。变桨控制存在不能控制沿叶片展向局部载荷波动、响应速度较慢和变桨零部件易过早磨损等缺点。智能叶片控制是十年前出现的更为先进的主动控制方法[1-2],智能叶片能精细快速的控制叶片的整体载荷及展向局部载荷,提高了叶片载荷的控制能力,此控制方法现已成为降低大型风力机载荷最有潜力方法。
智能叶片的执行机构有多种,包括可变形的尾缘襟翼、分离式尾缘襟翼和微型滑动襟翼[3]。李传峰等提出可变形尾缘襟翼能提高翼型的升力系数并降低风力机的波动载荷[4],Van Dam等研究了微型滑动襟翼,提出微型滑动襟翼可改善翼型表面压力系数分布,提高翼型的升力系数及升阻比[5-6]。Lee[7]等研究了运动尾缘襟翼,Lackner and Kuik[8]等研究了分离式尾缘襟翼对5 MW上风向风力机载荷的影响。
可变形的尾缘襟翼结构复杂,不易实现变角度控制;微型滑动襟翼响应速度快,但制造成本较高,分离式尾缘襟翼不但可以提高升力系数和升阻比,控制襟翼偏转角度也简单易行,还可以辅助变桨系统进行气动特性微调,其响应速度要比变桨系统响应速度要快。但是分离式尾缘襟翼在制造时不可避免的会出现襟翼与主体之间的缝隙,缝隙会对翼型的气动性能产生影响[9-10],高瑞峰研究了缝隙大小对高超声速分离流的影响,验证了缝隙存在改变了分离情况下翼面上的压力分布[11]。邓一菊等对于不同缝翼内型对多段翼气动性能影响进行了研究[12-13],韩中合等[14-15]研究了襟翼偏转角度及襟翼长度对翼型的气动性能的影响,对于缝隙大小对翼型气动性能的影响没有充分研究。目前不同的缝隙大小在对风力机翼尾缘襟翼的气动性能的影响方面研究尚属空白。为了设计合理的襟翼结构,有必要研究襟翼缝隙大小对翼型气动性能的影响。
文章以风力机翼型S809为基准翼型,建立了三种不同缝隙大小的尾缘襟翼模型及无缝隙的襟翼模型,襟翼长度为弦长的10%,偏转角为10°。计算分析了襟翼与主体之间的缝隙大小对尾缘襟翼气动性能的影响,为今后尾缘襟翼的结构设计、模拟计算及实际应用做好准备工作。
1 计算模型建立
1.1 几何模型
为了方便计算数据与试验数据比较,选取翼型S809作为研究的基准翼型。弦长设定为1000 mm,翼型最大厚度为210 mm。在基本翼型距尾缘10%c处增加襟翼,如图1所示。模型翼型本体与尾缘襟翼之间的缝隙采用CAD软件进行了局部优化处理,使得缝隙在整个分离面上分布均匀,且缝隙处曲线与襟翼上下翼面均相切。襟翼绕襟翼旋转中心向翼型压力面旋转,构成10°偏转角的分离式尾缘襟翼模型,如图2(a)所示,图中襟翼模型缝隙大小L分别为1‰c、2‰c、4‰c,图2(b)为无缝隙襟翼模型。

图1 带襟翼的S809翼型Fig.1 Airfoil S809 with flap

图2 S809尾缘襟翼计算模型Fig.2 Model of airfoil S809 with trailing edge flap
1.2 网格划分
在相同算法下,均匀分布的正交计算网格能获得高的计算精度[16],文章采用多块网格划分技术生成了正交性好的结构化网格。计算域分成半圆区域与矩形区域两部分,襟翼模型置于半圆圆心附近且水平放置,整个计算域采用C型网格拓扑结构进行网格划分,并在翼型的前缘、后缘、缝隙及襟翼连接处进行了局部加密。为避免入口和出口边界干扰,计算域入口段距翼型前缘20倍弦长,出口段距翼型后缘20倍弦长,上下边界分别为20倍弦长,定义计算域左边的半圆为速度入口,定义右侧边界为压力出口边界条件,定义翼型上下翼面为无滑移壁面条件。为较准确的模拟边界层内流动,翼型壁面附近第一层网格满足y+值在1附近。计算区域网格及翼型附近局部网格如图3所示。

图3 网格结构对比Fig.3 Comparison of grid structure
1.3 计算模型
Reynolds平均法(RANS)已经成为近年主要的流动分析计算方法,在各种湍流模型中,常用的计算模型有Spalart-Allmaras 提出的S-A一方程湍流模型与Wilcox提出的二方程湍流模型。Menter[17]混合采用k-ε和标准k-ω模型,得到了SSTk-ω模型,SSTk-ω模型合并了ω方程中的交叉扩散,并且考虑了湍流剪应力的传播,这些改进使得SSTk-ω模型比标准的k-ω模型具有更高的精度和可信度。该文采用了SSTk-ω湍流模型对尾缘襟翼模型流场进行了计算。
1.4 计算相关参数
雷诺数Re为2×106,收敛标准为计算残差小于10-6。无襟翼S809翼型迎角分别为0°、1.02°、5.13°、9.22°、14.24°、20.15°。三种带缝隙分离式尾缘襟翼模型以及整体式尾缘襟翼模型迎角0~18°,步长为2°。
2 计算模型可靠性分析
为证明所用算法的可靠性及合理性,对三种网格数、6种特定迎角下的气动性能计算结果与风洞试验数据[18-19]进行了对比。
首先对S809模型进行了网格无关性验证,选取三种网格数分别为10500、154800和254600,表1和表2分别为三种网格模型升力系数和阻力系数计算结果对比。由表1和表2表明网格数为10500模型计算的结果误差较其他两种网格数模型计算误差大一倍多,后两种网格计算误差近似相等。所以选取网格数为154800的模型作为计算网格即可保证较高的计算精度,又可以节约计算时间。
以网格数为154800的模型计算结果与风洞试验值进行对比分析。表1表明该模型升力系数的数值计算结果和试验值在低迎角时吻合很好,迎角0°时仅差0.9%,在失速迎角附近时误差稍大, 迎角20.15°时误差为8.06%;阻力系数计算值与试验值差值比升力系数的差值大,迎角0°误差为-4.3%,在失速迎角附近误差增大,当迎角为20.15°时误差为9.81%。虽然计算结果与试验结果存在一定偏差,但偏差值相对较小,而且文章主要研究襟翼与翼型主体间的缝隙大小对襟翼模型气动性能的影响,属于各种模型比较性研究,升阻力系数的偏差并不影响最终结论,表1和表2的升阻力系数对比结果表明,模型采用的算法是可靠的、合理的。
图4为不同迎角下S809计算模型计算结果和风洞试验结果的压力系数分布对比曲线图。图4表明计算模型的压力系数和试验数据有着相同的变化趋势,压力系数值稍有不同,但整体上和试验数据一致。

表1 升力系数比较Table 1 Comparison of lift coefficient
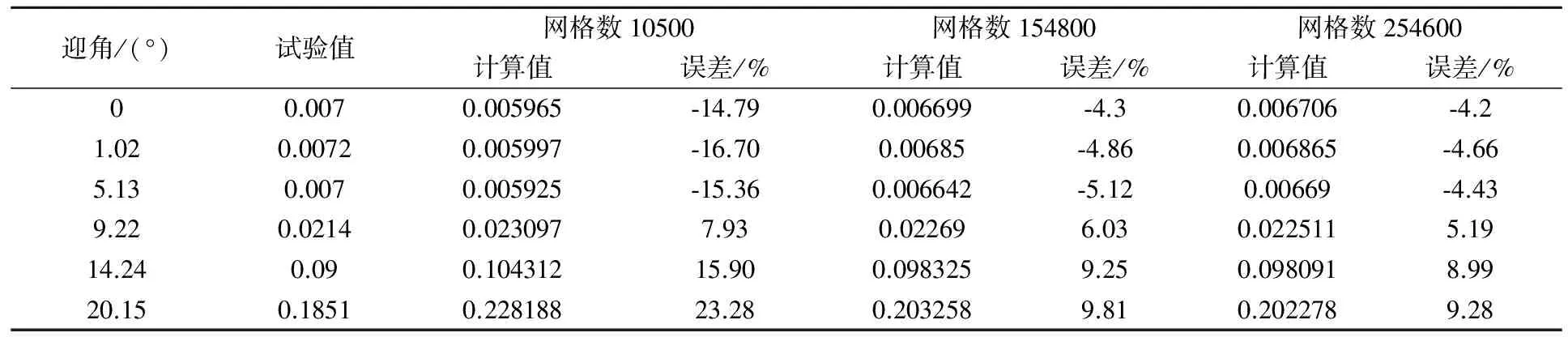
表2 阻力系数比较Table 2 Comparison of drag coefficient

(a) α=0° (b) α=5.13°

(c)α=14.24° (d)α=20.15°
图4无襟翼S809压力系数曲线
Fig.4CpdistributionsofairfoilS809withouttrailingedgeflap
从压力系数比较分析可判断,数值计算结果与试验值差值不大,襟翼模型所采用的算法是可靠的、合理的,可以满足模型计算要求。
3 计算结果分析
3.1 缝隙对上下翼面流场的影响
图5左至右分别为4‰c、2‰c、1‰c宽的缝隙襟翼模型和无缝隙襟翼模型流线图。从各个模型的流场情况可以看出,前两个模型对流场的影响明显,而缝隙为1‰c的模型与无缝隙模型的压力云图及流场的流线较为接近,表明随着缝隙的增加,缝隙对流场的影响增大,当缝隙小到1‰c时,缝隙对流场的影响很小。这是由于当襟翼与主体缝隙较小时,压力面的气流经缝隙至上翼面时,基本上沿切向流出,对于边界层的扰动较小,随着缝隙的加大,流体流出的方向与襟翼上翼面的平均夹角也增大,对于边界层的扰动增加,导致了流场变化较大。
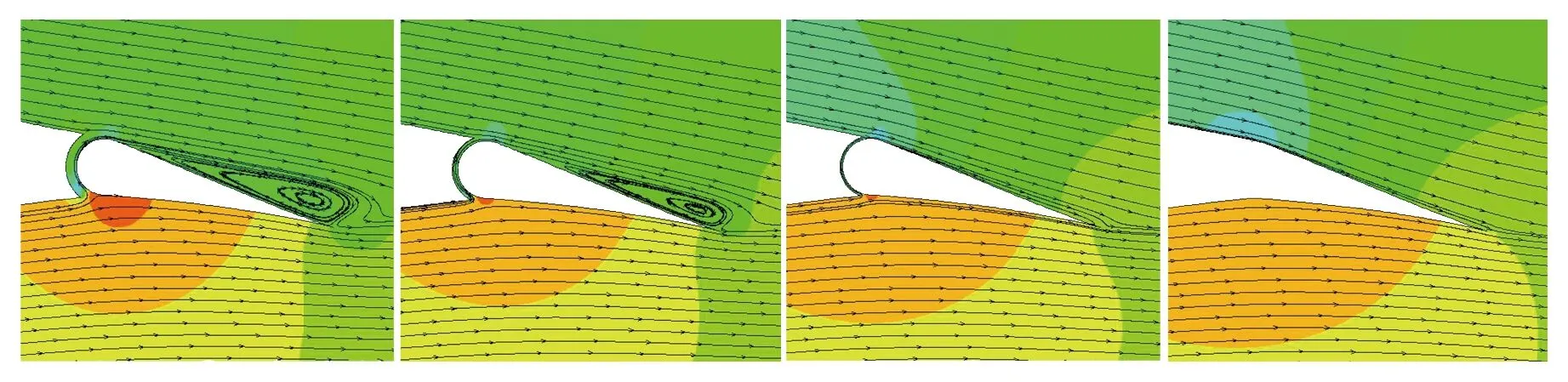
(a) 迎角0°

(b) 迎角4°

(c) 迎角8°

(d) 迎角12°
3.2 缝隙对压力系数分布的影响
图6为10%弦长、10°偏转角的三种缝隙襟翼模型和无缝隙襟翼模型在0°、4°、8°、12°迎角下压力系数比较图,图中without gap表示无缝隙襟翼模型压力系数,0.001cgap、0.002cgap、0.004cgap分别表示缝隙为1‰c、2‰c、4‰c宽的缝隙襟翼模型压力系数。由图6可以看出,无缝隙襟翼模型的上下翼面压力差大于有缝隙模型的上下翼面压力差,缝隙襟翼模型上下翼面的压力差随着缝隙的增加逐渐降低,所以升力系数也随之降低。小迎角范围内,随着翼型迎角的增大,缝隙的影响越来越小。2‰c、4‰c两种缝隙模型压力系数变化较明显,对翼型气动性能影响较大。而缝隙为1‰c的模型压力系数与无缝隙襟翼模型的压力系数很相近,说明缝隙小于等于1‰c时,缝隙对翼型的压力系数分布影响较小,此现象和升力系数曲线有类似趋势。

(a) 迎角0° (b) 迎角4°

(c) 迎角8° (d) 迎角12°
3.3 缝隙对升阻力系数的影响
3.3.1 缝隙对升力系数影响
图7为10%倍弦长、10°偏转角的三种缝隙襟翼模型、无缝隙襟翼模型及S809基准翼型在各个迎角下的升力特性对比曲线图,图中no flap 表示无襟翼的S809基准翼型计算数据,without gap表示S809无缝隙襟翼模型计算数据,0.001cgap、0.002cgap、0.004cgap分别表示三种不同缝隙的襟翼模型的计算数据。图7表明三种缝隙襟翼模型和无缝隙襟翼模型的升力系数在0°至18°迎角范围内均大于S809基准翼型的计算数据,有缝隙襟翼模型的升力系数小于无缝隙襟翼模型升力系数,且随着缝隙加大,升力系数减小的幅值也增大。0.002c与0.004c缝隙的模型升力系数比0.001c缝隙的模型升力系数有明显的降低。图7及图8表明随着迎角的增大,三种缝隙模型的升力系数差值逐渐减小,即缝隙的影响逐渐减小,当迎角大于10°以后,三者的升力系数差值又逐渐增大,即缝隙的影响随迎角的增加而增加,相同迎角下缝隙越大,升力系数降低幅值越大。缝隙为0.001c缝隙模型与无缝隙襟翼模型升力曲线趋势基本一致。在最大升力系数迎角14°时,升力系数比无缝隙襟翼模型降低0.85%,在常用的6°~18°迎角,升力系数降低值在0.35%~2%之间。所以对于缝隙小于0.001c的襟翼模型,在对其进行气动性能数值计算时,可以忽略缝隙的影响,可以采用无缝隙的襟翼来代替有缝隙的襟翼来分析,以降低网格划分的难度。而且在设计襟翼结构时,应尽量保证缝隙不大于0.001c,以降低缝隙对翼型的影响。
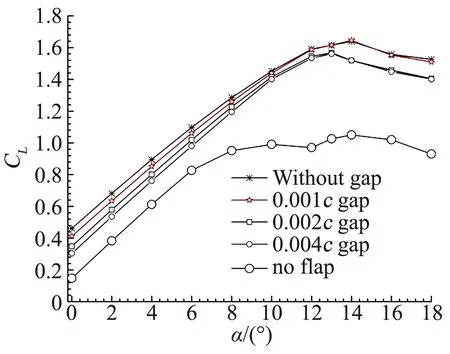
图7 不同模型升力特性对比Fig.7 Comparison curve of lift coefficients of different models
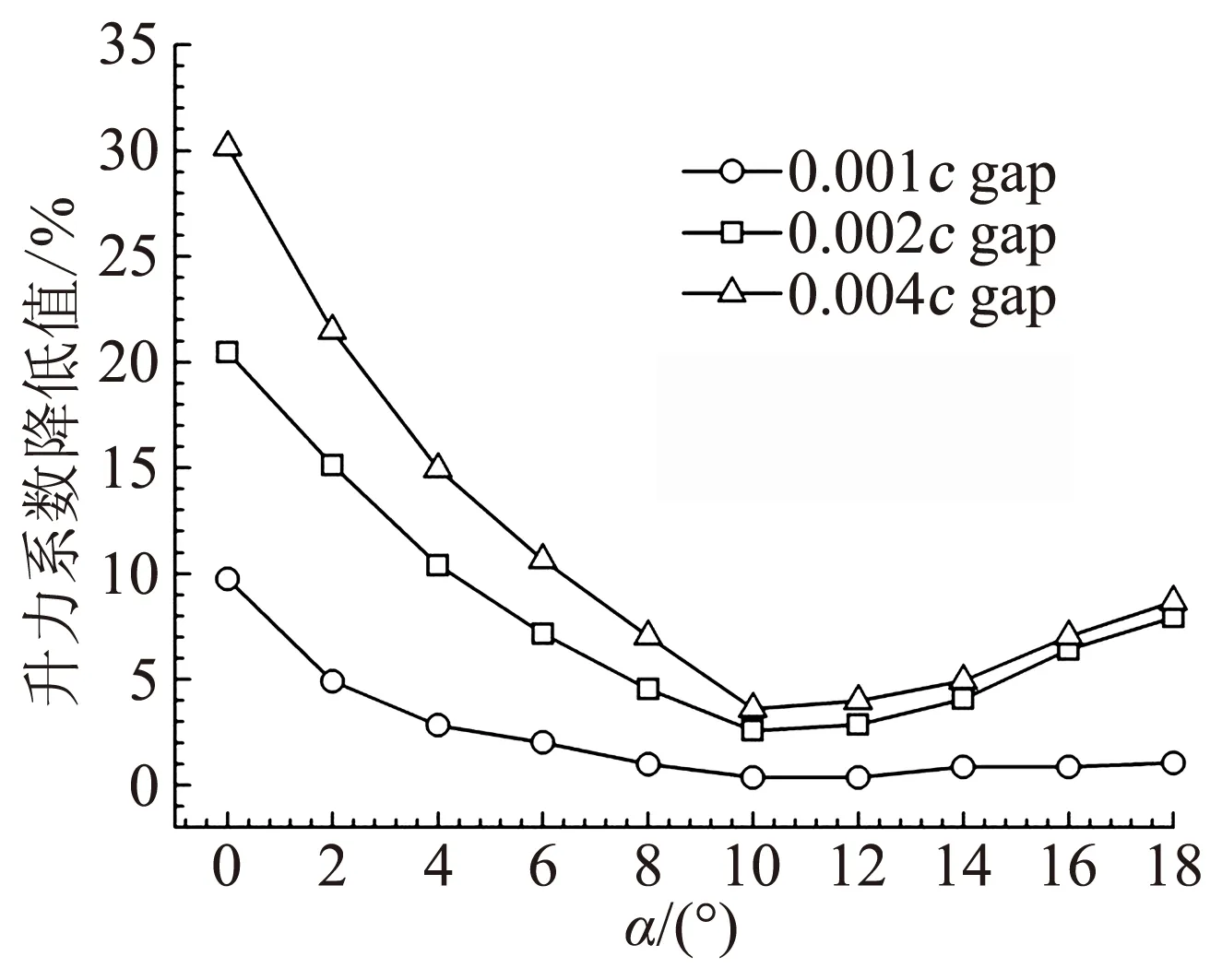
图8 不同模型升力系数变化对比Fig.8 Comparison curve of lift coefficients of different gap models
3.3.2 缝隙对阻力系数影响
图9为10%弦长10°偏转角的三种缝隙襟翼模型、无缝隙襟翼模型及S809基准翼型阻力特性对比曲线图,结果表明三种缝隙襟翼模型与无缝隙襟翼模型的阻力系数在0°~18°迎角范围内均大于S809基准翼型的计算数据,且随着迎角的增大,无襟翼模型阻力系数与襟翼模型阻力系数差值逐渐加大。三种缝隙模型的阻力系数在小迎角时均大于无缝隙襟翼模型阻力系数,且缝隙越大阻力系数越大,迎角为0°时三种缝隙模型与无缝隙模型阻力系数差值最大,缝隙为0.004c、0.002c、0.001c的襟翼模型比无缝隙襟翼模型分别大10.1%、5.3%、2.6%,且随迎角的增大,阻力系数差值逐渐减小,迎角大于10°后,有襟翼模型与无襟翼模型阻力相差接近于0,三种缝隙模型的阻力系数也相差很小。
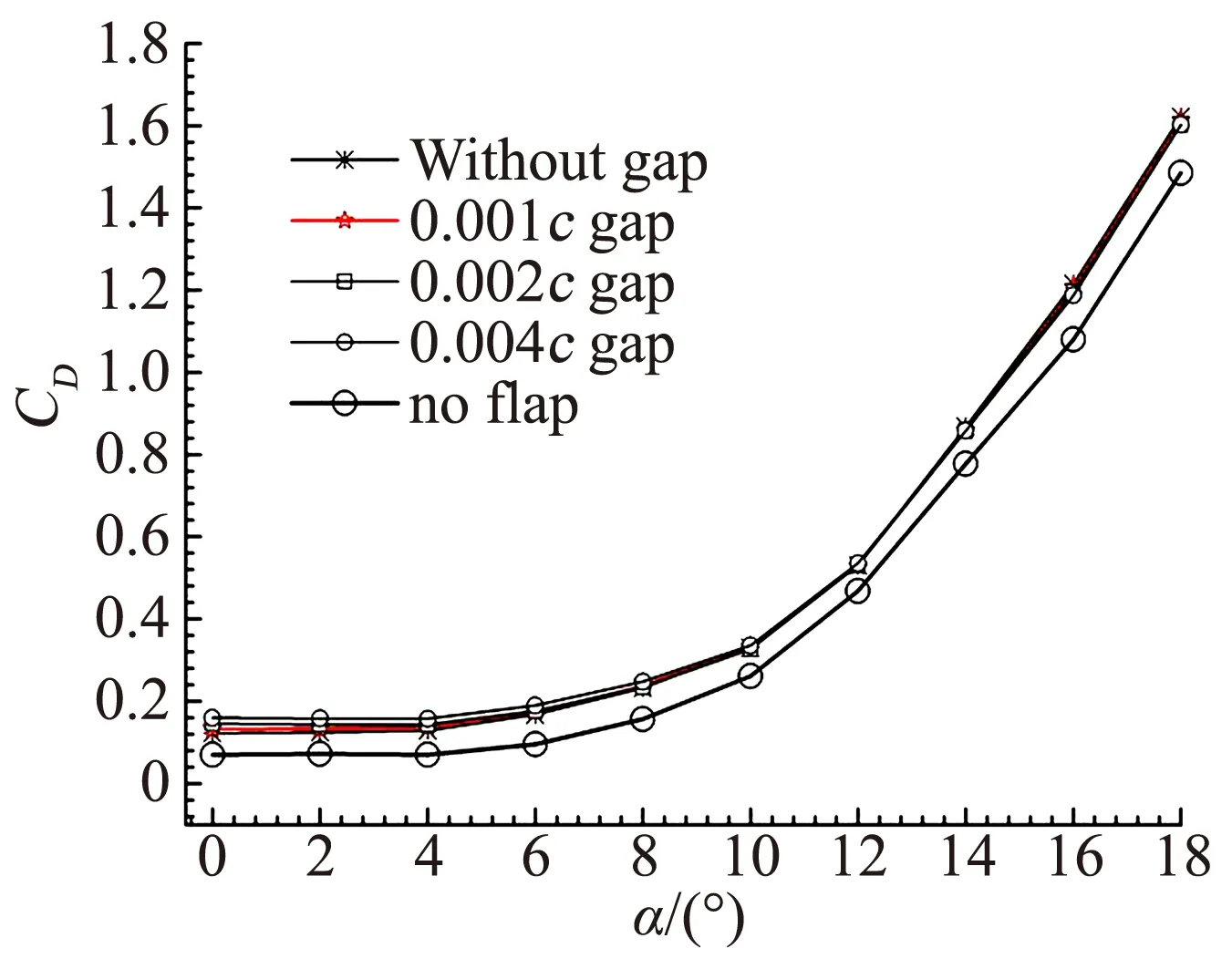
图9 不同缝隙模型阻力特性曲线Fig.9 Curve of drag coefficients of different gap models
3.3.3 缝隙对升阻比影响
图10为10%倍弦长10°偏转角的三种缝隙襟翼模型、无缝隙襟翼模型及S809基准翼型在各个迎角下的升阻比特性对比曲线图,图中no flap 表示S809基准翼型升阻比计算值,without gap表示S809无缝隙襟翼模型计算数据,0.001cgap、0.002cgap、0.004cgap分别表示三种不同缝隙的襟翼模型的计算数据。图10表明三种缝隙襟翼模型和无缝隙襟翼模型的升阻比在0°至4°迎角范围内均大于S809基准翼型的计算数据,有缝隙襟翼模型的升阻比小于无缝隙襟翼模型升阻比,且随着缝隙加大,升阻比减小的幅值也增大。0.002倍弦长与0.004倍弦长缝隙的模型升阻比比0.001倍弦长缝隙的模型升力系数有明显的降低。随着迎角的增大,三种缝隙模型的升阻比差值逐渐减小,即缝隙的影响逐渐减小,当迎角大于8°以后,三者的升阻比相差很小。缝隙为0.001c缝隙模型与无缝隙襟翼模型升阻比曲线趋势基本一致。最大的减小比例小于为3%,0.002c与0.004c与无襟翼升阻比最大减小比例19%和28%。
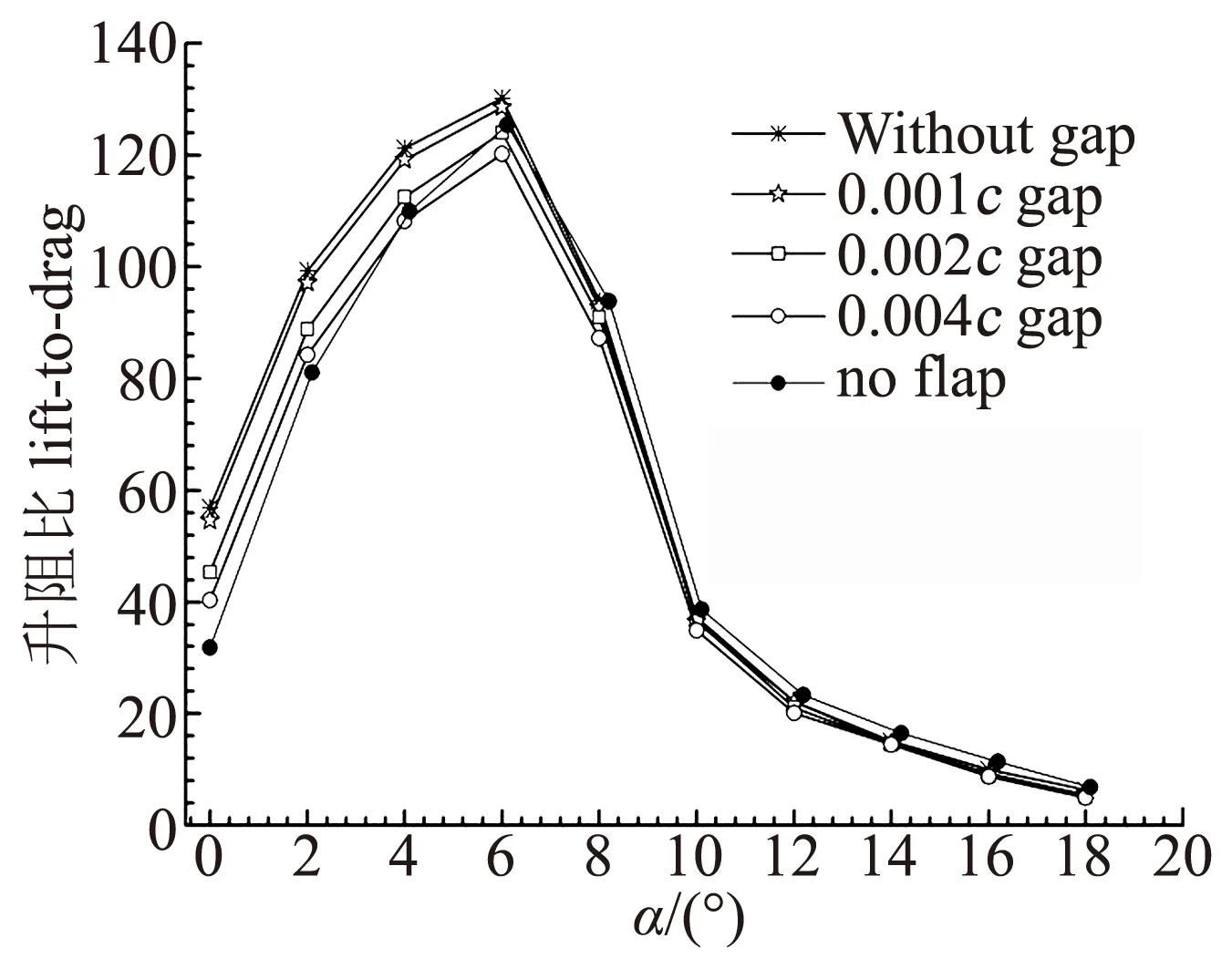
图10 不同缝隙模型升阻比特性曲线Fig.10 Curve of lift to drag of different gap models
4 结 论
文章研究了10°偏转角、三种缝隙宽度的10%弦长S809襟翼模型和无缝隙襟翼模型,对其在不同迎角下的流场及升阻力特性进行了对比,得出以下结论:
1) 翼型尾缘襟翼向压力面偏转可增大翼型的弯度,使翼型的升力系数增加,偏转角越大,升力系数也越大。
2) 缝隙的存在改变了压力面与吸力面的平衡,降低了升力系数,使得有缝隙襟翼模型的升力系数在一定迎角范围内小于无缝隙襟翼模型的升力系数,阻力系数在一定范围内大于无缝隙襟翼模型阻力系数。
3) 缝隙越小对翼型的升阻力系数影响越小,当缝隙为小到1‰c时,缝隙对翼型的气动性能影响很小,可以忽略不计,在襟翼结构设计时,可以作为设计参数参考。
4) 襟翼缝隙结构设计合理,使得下翼面的气体通过缝隙沿翼面的切向流出,降低了对翼型整体气动性能的影响。
[1]Barlas T K, Van Kuik G A M. State of the art and prospectives of smart rotor control for wind turbines[J]. Journal of Physics: Conference Series. IOP Publishing, 2007, 75(1): 012080
[2]Scott Collis S, Joslin R D, Seifert A, et al. Issues in active flow
control: theory, control, simulation, and experiment[J]. Progress in Aerospace Sciences, 2004, 40(4): 237-289
[3]Barlas T K, Van Kuik G A M. Review of state of the art in smart rotor control research for wind turbines[J]. Progress in Aerospace Sciences, 2010, 46(1): 1-27
[4]李传峰, 徐宇, 徐建中. 凹槽对风力机叶片尾缘襟翼性能的影响[J]. 工程热物理学报, 2011, 32(11): 1851-1854
[5]Baek P, M Gaunaa, Nn Sørensen, et al. Comparative study of distributed active load control concepts for wind turbine blades[J]. Science of Making Torque From Wind, 2010, 47(1): 611-617
[6]Johnson S J, Baker J P, Van Dam C P, et al. An overview of active load control techniques for wind turbines with an emphasis on microtabs[J]. Wind Energy, 2010, 13(2-3): 239-253
[7]Lee T, Su Y Y. Unsteady airfoil with a harmonically deflected trailing-edge flap[J]. Journal of Fluids and Structures, 2011, 27(8): 1411-1424
[8]Lackner M A, van Kuik G. A comparison of smart rotor control approaches using trailing edge flaps and individual pitch control[J]. Wind Energy, 2010, 13(2-3): 117-134
[9]Jose A I, Baeder J D. Steady and unsteady aerodynamic modeling of trailing edge flaps with overhang and gap using CFD and lower order models[C]//47th AIAA Aerospace Sciences Meeting, Florida, AIAA-2009-1071, 2009
[10]Jose A I, Mishra A, Baeder J D. An investigation into the aerodynamics of trailing edge flaps with overhang and gap[C]//AHS Specialist’s Conference on Aeromechanics, San Francisco, 2008
[11]高瑞峰. 缝隙大小对高超声速分离流的影响[J]. 空气动力学学报, 1988, 6(1): 128-131
[12]邓一菊, 廖振荣, 段卓毅. 前缘缝翼内型的气动设计研究[J]. 空气动力学学报, 2014, 32(3): 400-404
[13]Wang W, Liu P, Tian Y, et al. Numerical study of the aerodynamic characteristics of high-lift droop nose with the deflection of fowler flap and spoiler[J]. Aerospace Science and Technology, 2016, 48: 75-85
[14]韩中合, 贾亚雷, 李恒凡, 等. 风力机分离式尾缘襟翼气动性能[J]. 农业工程学报, 2014, 30(20): 58-64
[15]韩中合, 贾亚雷, 李恒凡, 等. 尾缘襟翼长度对风力机翼型气动性能的影响[J]. 空气动力学学报, 2015, 33(6): 835-842
[16]李银然, 李仁年, 王秀勇, 等. 计算模型维数对风力机翼型气动性能预测的影响[J]. 农业机械学报, 2011, 42(2): 115-119
[17]Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605
[18]Hand M, D Simms, Lj Fingersh. Unsteady aerodynamics experiment phase VI: wind tunnel test configurations and available data campaigns. NREL[R]. T P-500-2995, 2001
[19]Wolfe W P, Ochs S S. CFD calculations of S809 aerodynamic characteristics[R]. Sandia National Labs., Albuquerque, NM (United States), 1997.

