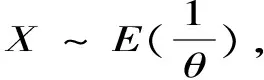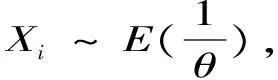伽玛概率分布性质研究
高显彩,单雪红
(宿州学院 数学与统计学院,安徽 宿州 234000)
0 引言
在文献[1]—[4]中都提出了一种重要的概率分布,称之为伽玛分布,为书写方便记为Γ-分布,本文将对此概率分布作进一步的分析.
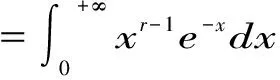
(2)Γ(r+1)=rΓ(r),当r为自然数n时,有Γ(n+1)=nΓ(n)=n!)
概率密度函数f(x)的性质:
0 r=1时,f(x)是严格下降的函数,且在x=0处f(0)=λ; 1 伽玛分布的可加性[4]: 设X~Γ(r1,λ),Y~Γ(r2,λ),且X与Y相互独立,则Z=X+Y~Γ(r1+r2). 这正是形状参数为r1+r2,尺度参数为λ的伽玛分布. 这个结论可推广到有限个尺度参数相同的独立伽玛变量之和.即 Γ-分布在概率论、数理统计和随机过程中都有应用. 例1[1]:电子产品失效往往是因为外界的冲击所引起,如果在(0,t)内发生的冲击次数N(t)服从参数为λt的泊松分布,则第n次冲击来到的时间Sn服从Γ(n,λ). 证明:因为事件“第n次冲击来到的时间Sn小于等于t”等价于事件“(0,t)内发生冲击的次数N(t)大于等于n”,即{Sn≤t}={N(t)≥n} 以(1,λ)为参数的Γ-分布,就是以λ为参数的指数分布,又在泊松过程中,等待n个“事件”发生所需的时间就服从参数为(n,λ)的Γ-分布.或者说n个独立的参数为λ的指数分布的随机变量之和就是一个参数为(n,λ)的Γ-分布的随机变量. 爱尔朗分布与指数分布有着密切关系,如果输入分布是指数分布,顾客独立到达,则输入r个顾客的时间分布即为r阶爱尔朗分布. 定理1[7]:设ξ1,ξ2,…,ξr是相互独立、服从相同参数λ(>0)的指数分布的随机变量,则ξ=ξ1+ξ2+…+ξr服从r阶爱尔朗分布. 假定r=k时,ξ=ξ1+ξ2+…+ξk的密度函数为 当r=k+1时ξ=ξ1+ξ2+…+ξk+1的密度函数为 结论得证,即ξ=ξ1+ξ2+…+ξr服从r阶爱尔朗分布. 由此结论可知,r个相互独立且服从指数分布的随机变量之和即为一个r阶爱尔朗分布.爱尔朗分布虽然不具有无记忆性,但是爱尔朗分布与指数分布有密切的联系,所以我们可以利用指数分布的特性来处理与爱尔朗分布有关的问题. 由中心极限定理可知,若随机变量ξ服从r阶爱尔朗分布,则对一切x≥0,有 定理2[4]:如果ξ服从标准正态分布,则ξ2服从λ=0.5,r=0.5的Γ-分布, 即ξ2~χ2(1). 所以ξ2服从λ=0.5,r=0.5的Γ-分布,即ξ2~χ2(1). 恰好为标准正态分布的特征函数,由逆极限定理可知:伽玛分布在r→∞时渐进正态分布. 当y<0时,fY(y)=0. [1] 茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2004. [2] 严士键,刘秀芳,徐承彝.概率论与数理统计[M].北京:高等教育出版社,2011. [3] 何书元.概率引论[M].北京:高等教育出版社,2011. [4] 袁荫棠.概率论与数理统计(第二版)[M].北京:中国人民大学出版社,1998. [5] 陶会强.常用概率分布之间的关系及应用研究[J].怀化学院学报,2011,30(5):75-78. [6] 王红雁.Γ-函数在概率统计中的应用[J].高等数学研究,2014,17(3):29-30. [7] 唐应辉,唐小我.排队论:基础与分析技术[M].北京:科学出版社,2006.
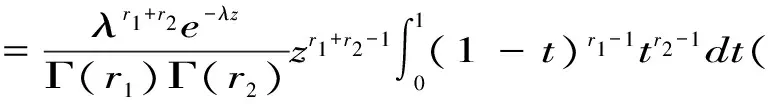

1 伽玛分布的应用



2 各分布之间的关系
2.1 伽玛分布与指数分布

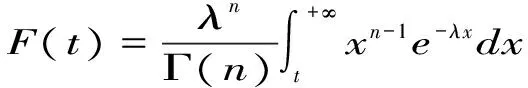
2.2 爱尔朗分布与指数分布

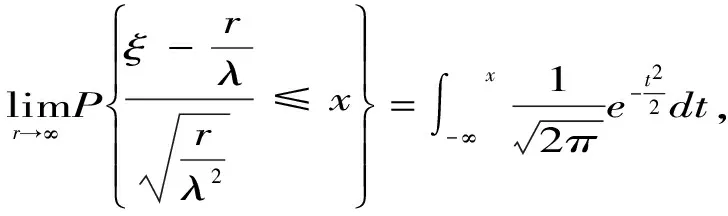
2.3 伽玛分布与正态分布

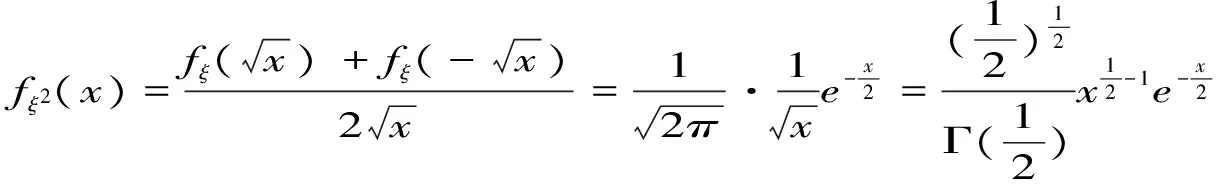
2.4 伽玛分布渐进正态分布

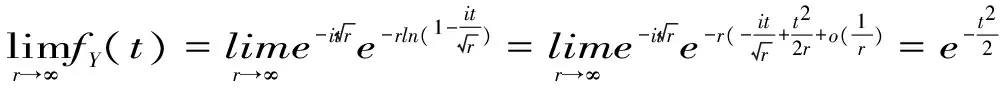
2.5 伽玛分布与χ2分布


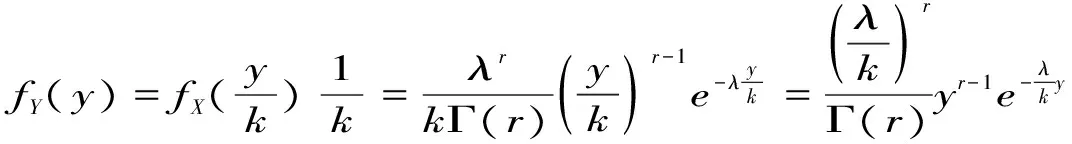
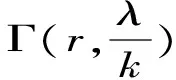
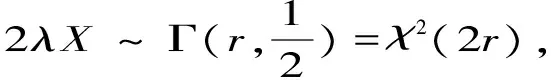
3 举例