可逆矩阵算法研究

宋晓辉

(郑州工业应用技术学院 基础教学部，河南 郑州 451150)

0 引言

矩阵理论不仅在数值分析、微分方程、控制论等数学学科有广泛的应用，而且在经济管理、社会科学等领域也起着重要的作用.矩阵的可逆在矩阵理论中占有很重要的地位，在数学的学习中，矩阵的可逆只是从理论上阐述了其方法，随着科学技术的发展，理论与实际结合更加密切，求逆矩阵的方法也在不断更新，所以我们有必要进一步去研究学习，来丰富发展逆矩阵的知识.

1 可逆矩阵的求法

1.1 利用线形方程组求逆矩阵

若n阶矩阵A可逆，则AA-1=E，将A-1和E以列分块，

Aξ1,ξ2,···,ξn=ε1,ε2,···,εn

(1)

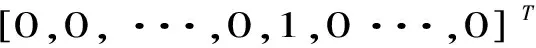
(i=1,2,...,n)的解.

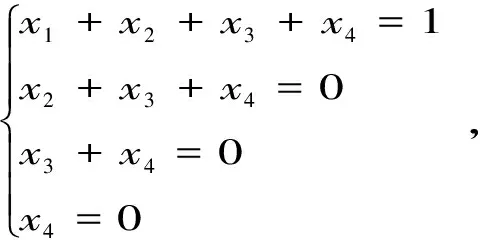
同理可求得

故

1.2 行列同时变换法

解

即

所以

1.3 分块矩阵法[1]

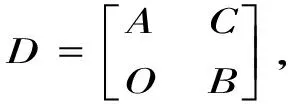
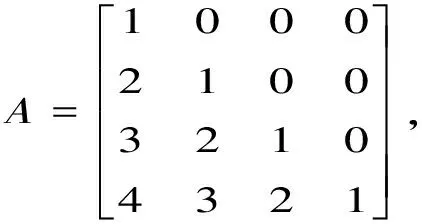
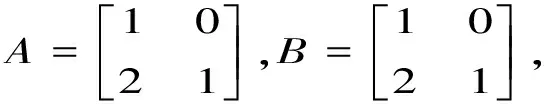
则

所以

1.4 Hamilton-Caylay定理求逆矩阵

Hamilton-Caylay

定理[3 ]设A是n阶方阵，A的特征多项式为fλ=λE-A，则

设n阶方阵A的特征多项式

fλ=A-λE=C0+C1λ+···+Cnλn，

令λ=0，得A=C0.可见A可逆的充要条件是C0≠0.当A可逆时，由

fA=C0E+C1A+···+CnAn，

得

所以

2 可逆矩阵的应用

可逆矩阵在保密通信中的应用[4 ].保密通信是信息社会非常重要的课题，其中基于加密技术的加密保密通信模型是最基本、最重要的一种.

2.1 加密保密通信模型

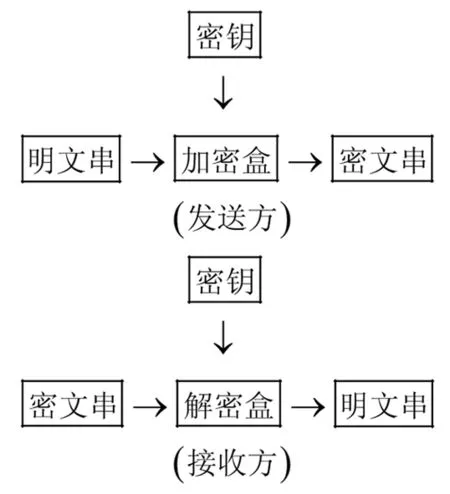
图1 基于加密技术的保密通信模型

2.2 可逆矩阵的应用

密文能否还原成明文决定了加密技术是否有效.设矩阵C=AB，其中矩阵B未知，若矩阵A可逆，则方程有唯一解B=A-1C.因此，可逆矩阵可以应用于加密技术.

2.2.1 加密算法

加密时，采用下面的矩阵乘法:C=BA或C=AB.

若设加密密钥矩阵A为

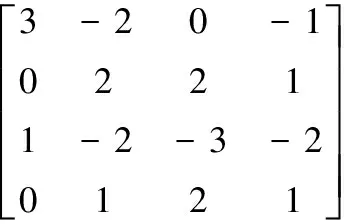
明文矩阵B为

则密文矩阵

2.2.2 解密算法

解密时，采用下面的矩阵乘法：B=CA-1，B=A-1C其中，A-1为A的逆矩阵.

如加密矩阵A为

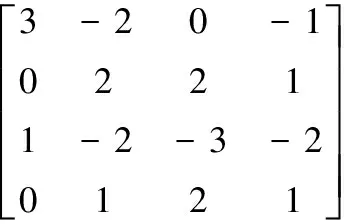
则解密矩阵A-1为

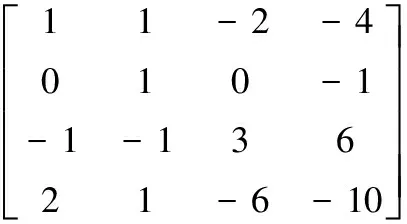
若密文矩阵

则明文矩阵

[1]陈瑞,王星星.矩阵可逆的若干判别方法研究[J].枣庄学院学报,2017,34(2):69-70.

[2]同济大学数学系.工程数学线性代数(第六版)[M].北京:高等教育出版社,2014:156.

[3]北京大学数学系几何与代数研究室前代数小组.高等代数[M].北京:高等教育出版社,2003:378.

[4]熊小兵.可逆矩阵在保密通信中的应用[J].大学数学,2017,23(3):108-109.