超材料介质基底对结构谐振特性的影响

张永刚

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

0 引言

超材料是指人工设计的结构，呈现出自然材料不具备的物理性质特别是电磁特性的一类电磁材料.所以人们可以通过裁剪超材料的结构得到自然界中没有的电磁特性，如负折射率等[1-4].超材料特殊的物理特性通常是在其谐振状态下表现出来的，而超材料的谐振特性与其金属结构以及金属结构周围介质有关[5].超材料的单元结构大小要比电磁波波长小的多，这使得结构间的耦合是很大而不能忽略的[6-8]，由耦合产生的影响会使结构出现一些新的物理现象，比如谐振频率的变化等[4].

其它一些因素也会对其谐振特性产生影响，金属结构的介质基底是其中重要的影响因素之一.这里我们采用电路模型分析了超材料中介质基底对其物理特性的影响.电路模型是把超材料的谐振子等效为RLC谐振电路并进行分析.在建立电路模型时，把金属结构的损耗用电阻R(这个损耗包括欧姆损耗和辐射损耗)来等效.超材料表现出电感效应和电容效应分别用电路参数L和电容参数C来表征.超材料金属结构在电路模型中用电阻R、电感L和电容C的串联电路来描述.

本文针对双层U形环结构，把基底影响等效成电路模型中的电容参数，通过研究电容参数的变化分析超材料介质基底对结构谐振特性的影响.然后利用仿真软件计算超材料有无介质基底时结构的谐振特性的区别.

1 电路分析

我们采用一种双层的金属U形环结构，结构采用金制备，两层环的几何结构完全相同，如图1所示.如果上下两层金属环两侧介质的介电常数和厚度都相同，则两侧介质对上下两层U形环的影响是完全一样的.相反，如果两层U形环两侧的介质不同：例如结构制备在硅介质基底上，则上层U形环上侧是空气，下层环的下侧是基底硅.硅和空气的介电常数差别较大，而且空气层的厚度可以看成无穷大，所以它们对两层金属环的电磁影响是不同的.

图1所示的两层金属结构的两侧的介质如果存在差别，对两层金属环的电磁影响不同的原因是电场穿过不同介电常数或不同厚度的介质造成的电磁场效应存在差别.在电路模型中的这种差别可以用电容效应的不同来描述.建立该结构的电路模型时，把这种差别描述为其电路方程中的等效电容值的不同.可以设一个U形环的等效电路的电容为C1，另一个U形环的等效电路方程中的电容为C2，得到双层U形环耦合的等效电路模型，如图2示.

图1 双层U形环的单元结构示意图 图2 双层U形环等效电容值不同的电路模型

根据等效电路模型，可以建立其电路方程.在图2中，设左中右三个网孔电流分别为I1、I、I2，且电流顺时针方向为参考方向，可以建立如下的方程.

(1)

(2)

(3)

(4)

下面讨论电流I2模值与参数η的关系.

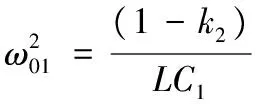
(3)当η>1时，分析电路方程得到ξ有两个解，设这两个解为ξ1，ξ2，于是有ξ1=-ξ2，电流取最大值，即电流的曲线出现双峰.

2 模拟仿真

我们采用仿真软件计算了周期结构的太赫兹频率下硅介质基底上双层U形环间耦合的透射谱.每个金属U形环单元结构如图1所示.单元的周期为80 (m.单元结构其它参数值分别为：a = 40 μm, b = 25 μm, d =10 μm, w =15 μm, h = 0.2 μm, t = 10 μm.两个环间隔介质采用聚酰亚胺，介电常数为3.1，聚酰亚胺厚度为10 μm.设入射波为平面极化波，电场偏振方向垂直U形环的缝隙，磁场偏振方向垂直于U形环的两个臂.

图3 (a)：无硅介质基底，环间的角度为0°时的透射谱；(b)：无硅介质基底，

首先，我们计算了双层环结构在没有介质基底情况下，双层U形环在不同旋转角度下的透射谱.图3(a)是结构在没有硅介质基底时的透射谱(两层环之间的角度为0°).图3(b)为两层U形环间的旋转角度与谐振频率之间的关系，两层环之间的旋转角度(从0°到180°，等间隔选取19个点)得到结构谐振频率的变化，可以看出在旋转角度大约在43°到56°这一段，结构的两个谐振频率变成一个.通过前面的电路分析可以知道，在这一段角度，有η≤1时，且C1= C2，于是电流谱中的两个谐振峰相等.这说明我们的仿真结果和前述电路分析是一致的.

3 总结

本文针对双层U形环结构的耦合，建立了其等效电路模型.把超材料基底对其物理特性的影响等效成电路模型中的电容参数.从分析结果可以看出由于电容C的不同，两层U形环之间夹角的变化虽然也能导致谐振频率的变化.但在旋转角度的整个变化过程中，结构都会有两个谐振频率的出现.而这种电容参数C的区别实际上体现了超材料金属结构介质基底的区别.研究结果说明超材料超的介质基底是对其物理特性，特别是谐振特性有很大的影响.介质基底同样是进行超材料分析设计时不能忽视的影响因素.

[1] Veselago V G, The Electrodynamics of substances with simultaneously negative values of ε and μ [J]. Sov. Phys. Usp, 1968, 10:509-514.

[2] Smith D R, Padilla W J, Vier D C, Nemat-Nasser S C, Schultz S, Composite medium with simultaneously negative permeability and permittivity [J]. Phys. Rev. Letts, 2000, 84: 4184- 4187.

[3] Shelby R A, Smith D R, Schultz, Experimental verification of a negative index of refraction [J]. Science, 2001, 292:77-79.

[4] Zhou J F, Zhang L, Tuttle G, Koschny T, Soukoulis C M, Negative index materials using simple short wire pairs [J]. Phys. Rev. B, 2006, 73:041101.

[5] Liu N, Giessen H. Coupling effects in optical metamaterials angewandte chemie international edition [M]. Wiley Online Library, 2010.

[6] Liu N, Guo H, Fu L, Schweizer H, Kaiser S, Giessen H, Electromagnetic resonances in single and double split-ring resonator metamaterials in the near infrared spectral region [J]. Phys. Status Solidi B, 2007, 244:1251-1255.

[7] Rockstuhl C, Zentgraf T, Guo H, Liu N, Etrich C, Loa I, Syassen K, Kuhl J, Lederer F, Giessen H, Resonances of split-ring resonator metamaterials in the near infrared [J]. Appl. Phys. B, 2006, 84: 219-227.

[8] Liu N, Guo H C, Fu L W, Kaiser S, Schweizer H, Giessen H, Three-dimensional photonic metamaterials at optical frequencies [J]. Nature Material, 2008, 7: 31-37.