离散Kepler系统的共形不变性与守恒量
夏丽莉, 张 伟
(1.北京工业大学 机械工程与应用电子技术学院 北京 100124; 2.河南财政金融学院 物理与电子工程学院 河南 郑州 450046)
0 引言
共形不变性是寻求守恒量的现代方法, 是建立在标度不变性、 平移不变性、 转动不变性和短程相互作用基础之上的一种对称性理论. 文献[1]研究了Birkhoff系统的共形不变性, 讨论了共形不变性与Lie对称性之间的关系. 文献[2-3]给出了 Mei对称性共形不变性的定义和判据方程. 人们对连续系统的共形不变性和守恒量理论进行了大量的研究, 并取得了相当多的成果,但对于离散力学系统的共形不变性和守恒量理论研究较少.文献[4]结合文献[5]的研究方法, 在连续系统共形不变性基础上, 研究离散 Lagrangian系统的共形不变性和Noether守恒量.
经典Kepler问题在天体力学和量子力学中被广泛关注,守恒量理论一直是Kepler问题研究的重点内容[6]. 文献 [7] 得到了能量守恒、角动量守恒和Runge-Lenz矢量守恒. 虽然Kepler系统的连续对称性问题得到了一定的发展, 但对于Kepler系统的离散共形不变性尚无报道. 离散化方法在数学、物理等领域发挥着重要的作用[8]. 本文基于Kepler系统的离散化理论[9],通过研究Kepler系统的共形不变性,得到了一种更加简洁的探究Kepler系统的守恒量的路径.
1 离散Kepler系统的运动方程
(1)
在离散变量空间中, 离散变量形式为(t-,t,t+,t++,…,q-,q,q+,q++,…),n维坐标变量q={q1,…,qn},p={p1,…,pn}.这里采用“改良版本”的离散Legendre变换离散Kepler系统的Hamilton函数,可以表示为
(2)
则离散Kepler正则方程可以表示为
(3)
(4)
2 离散Kepler系统的共形不变性
令矩阵
(5)
相空间中无限小生成元向量的离散点扩展式为
(6)
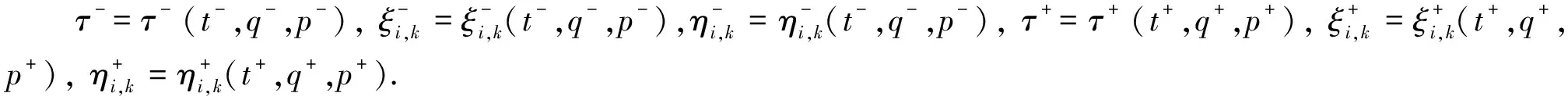
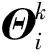
(7)
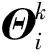
3 共形不变性和Lie对称性
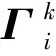
(8)
则系统的共形不变性是Lie对称性的充要条件为
(9)
证明根据Lie对称性定义, Kepler系统的Lie对称性满足:
(10)
4 Kepler系统的共形因子
Kepler系统的动力学方程可以表示为
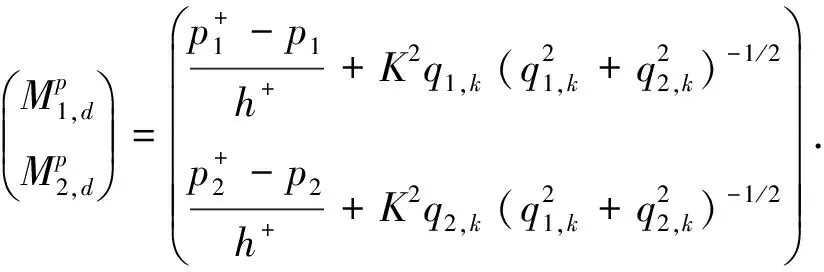
(11)
取无限小生成元τ=0,ξ1=-q2,k,ξ2=q1,k,η1=-p2,k,η2=p1,k, 有
Kepler系统的共形因子为
5 Noether守恒量
Noether 对称性原理表明:作用量的每一种连续对称性都有一个守恒量与之对应. 人们把这种对称与守恒量的联系称为 Noether 定理[10], 对于离散动力学系统的积分理论, 文献[11]给出了离散 Hamilton系统的Noether定理.
定理2[11]如果存在无限小生成元ξ、ηi、ζi和规范函数Gi=Gi(t,t+,q,p+)满足离散Noether等式:
(12)
则Hamilton系统导致如下守恒量:
(13)
定理3如果无限小生成元ξ、ηi、ζi满足方程(10), 存在规范函数Gi=Gi(t,t+,q,p+) 满足离散Noether等式 (12), 则Hamilton系统的Lie对称性共形不变性导致守恒量(13).
(14)
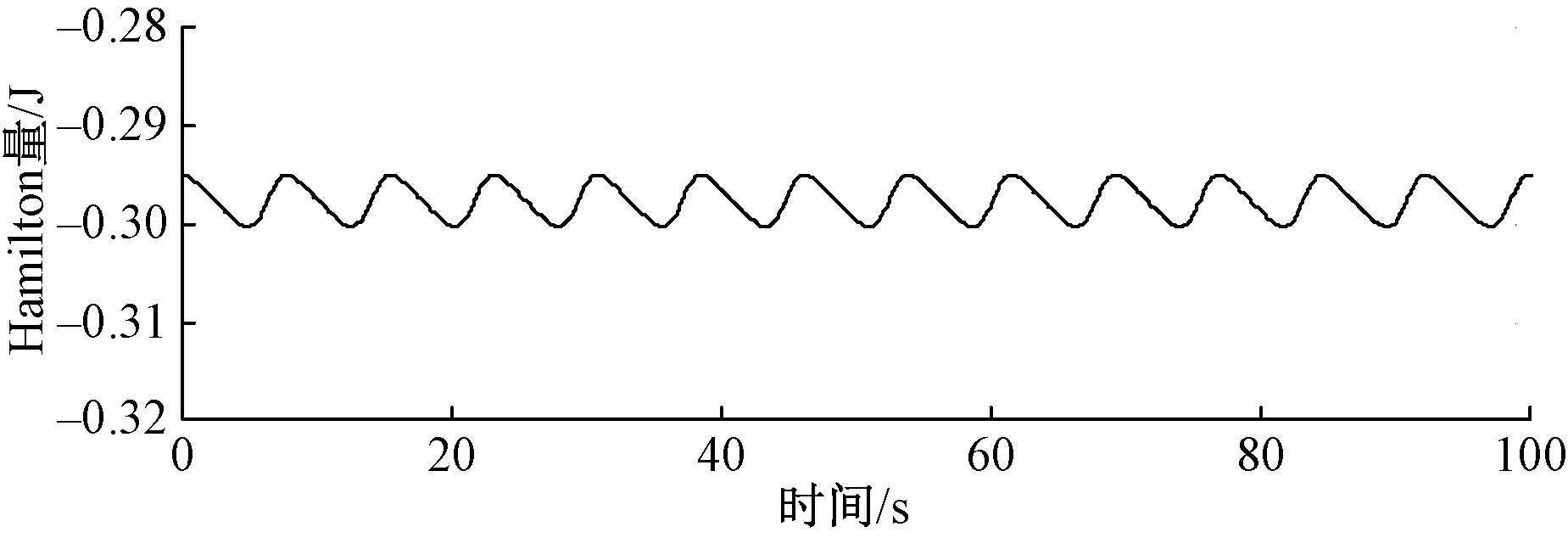
图1 离散变分方法求解Noether守恒量的放大图Fig.1 Amplified image of the Noether conserved quantity by the discrete variational method
这里,定理3说明取不同的对称性生成元和合适的规范函数, 可能得到更多的守恒量. 本文只给出了能量守恒.
选择初始条件为q1=0.003,q2=0.9,q3=0.01,p1=0.1,p2=0.1和p3=0.8的Kepler轨道,并取步长为0.1, 常数K=0.75. 根据Nother定理得到守恒量(14),即系统的Hamilton量.图1给出了通过离散变分方法模拟系统的Hamilton量随时间的变化趋势.
6 结论
引入离散差分变分原理研究离散Kepler系统的共形不变性和守恒量理论, 得到了系统的共形因子. 基于Hamilton系统的离散Noether定理, 得到了Kepler系统的守恒量,并用基于离散变分原理的保结构数值算法验证了系统的守恒量.
[1] GALIULLIN A S, GAFAROV G G, MALAISHKA R P, et al. Analytical dynamics of Helmholtz, Birkhoff and Nambu systems[M]. Moscow:UFN, 1997.
[2] CAI J L. Conformal invariance and conserved quantities of Mei symmetry for Lagrange systems[J]. Acta physica sinica, 2009, 115 (5): 854-856.
[3] 蔡建乐. 一般完整系统 Mei 对称性的共形不变性与守恒量[J]. 物理学报, 2009, 58 (1): 22-27.
[4] XIA L L, CHEN L Q. Conformal invariance of Mei symmetry for discrete Lagrangian systems[J]. Acta mechanica, 2013, 224(9): 2037-2043.
[5] DORODNITSYN V A. Finite-difference analog of the Noether theorem[J]. Doklady physics, 1993, 38 (2): 66-68.
[6] THIRRING W. A course in mathematical physics: classical dynamical systems[M]. New York: Springer-Verlag, 1978.
[7] KOZLOV R. Conservative discretizations of the Kepler motion[J]. Journal of physics A: mathematical and theoretical, 2007, 40(17): 4529-4539.
[8] 朱维军, 周清雷. 一种时间自动机时钟离散化算法[J]. 郑州大学学报(理学版),2011, 43(3): 75-77.
[9] 刘长欣,裴利军,夏丽莉. Kepler问题的离散化和积分理论[J]. 郑州大学学报(理学版),2016,48(2):29-33.
[10] NOETHER E. Invariante variationsprobleme[J]. Gott Nachr, 1918, 1(2): 235-257.
[11] DORODNITSYN V, KOZLOV R. First integrals of difference Hamiltonian equations[J]. Journal of physics A: mathematical and theoretical, 2009, 42 (45): 454007.

