丹克斯的图模型认知表征研究

范 莉,闫 鼎

(山西大学 哲学社会学学院，山西 太原 030006)

在认知科学哲学中，认知的统一性问题是人类精神统一性研究的重要议题，对它的探讨有助于解释两种认知现象：一是不同的认知过程之间以相对无缝的方式转换；二是认知在复杂环境中准确搜集信息。认知统一理论认为，认知的各组成部分具有共同的基础[1]。认知具有稳定性、持久性、跨多认知过程的特征，本身具有统一性。一般认为，认知统一理论主要有两条径路：一类是以图式为中心的联结主义、贝叶斯主义；另一类是以过程为中心的ACT-R、Soar、Sigma理论。大卫·丹克斯(David Danks)。在他的《认知统一性——作为图模型的认知表征》一书中，提出一种互补于以上两条径路的、以共享表征为中心的径路——图模型的认知表征。

人类每天都要面临大量的人类活动：“分类对象、对它们进行推理、学习它们之间的因果关系、在因果信念下计划并行动、观察并分类行为的结果，从结果中学习等。”[2]1图模型认知表征理论认为，这些认知活动都以图模型计算为共同基础，并具有统一性。它承袭了计算表征主义的核心思想，认为“任何认知过程能够通过一个可计算函数进行表征”[3]105。不过，与以往计算表征主义不同的是，图模型认知表征的计算工具是图模型，它认为，不同的认知过程是以图模型的运算方式来表征的。

一、图模型与表征

丹克斯用图模型表征来构建认知统一框架。在这个框架中，思维是对外部世界的反映，并作为一个整体指导行为作用于外部世界。思维主要的认知过程有因果认知、概念获得、决策等。因果认知，基于概念、基于决策等认知过程都共享一个以图模型为表征结构的共享表征库，在这个共享表征库中，实现了认知统一的理论目标。

图模型是一种数学计算工具，最近才被用于认知科学的研究[2]6。图模型是对相关关系的表征。在认知科学中，它用来表征认知过程中的相关关系。例如，撞击导致受伤，用图模型对这种相关关系的认知表征是：撞击→受伤。

图模型由图和定量信息两部分组成。其中，图的部分编码是关于各要素之间结构的定性信息；定量信息是对关系强度的定量表征。

一方面，图由节点和边两部分组成。即它利用节点和边来对定性关系进行编码，例如图1。

图1 有向无圈图

在图1中，A、B、C为节点，连接在它们之间的线段就是边。从纯数学视角来看，节点代表对象，边代表对象之间的相关关系。这种相关关系有三种类型：一是有向边(A→B)类型，二是无向边(A—B)类型，三是双向边(A↔B)类型。边的方向表征了相关关系的不同方向。 边所连接的两节点具有相邻关系，也就是说，当且仅当两点之间有一条边时，这两点是相邻的。从语义学的视角来看，图模型中的节点表征个体、变量等。边表征直接的相关性，例如，直接原因、直接交流或社会联系、直接的或或然的相关性或其它类型的直接关联等。

另一方面，对于定量信息，它是对定性的相关关系的补充，是构成一个完整图模型的必要组成。定量信息的补充，可以使得图模型在计算上更加精确。定量信息中蕴含着节点间独立或者相依的相关关系。两个相邻节点之间具有相依关系，不相邻的节点之间具有独立关系。在图模型中，两个原本相依的节点，一旦在之间添加了其它的节点，那么原本相依的节点就成为独立的了。例如，在图1中，如果没有节点B，那么A和C就是相依的，一旦知道了B的意义，那么A和C就成为独立关系。也就是说，在图模型中，只有相邻的两个节点才具有直接的相依关系。这使得图模型具有模块化的特征。即图模型可以在局部的模块上精确预测、推理运算，因为预测一些节点的意义只需要知道相邻节点的意义。例如，在图2中，预测节点A，只取决于B、C、D，而与其他任何节点无关。

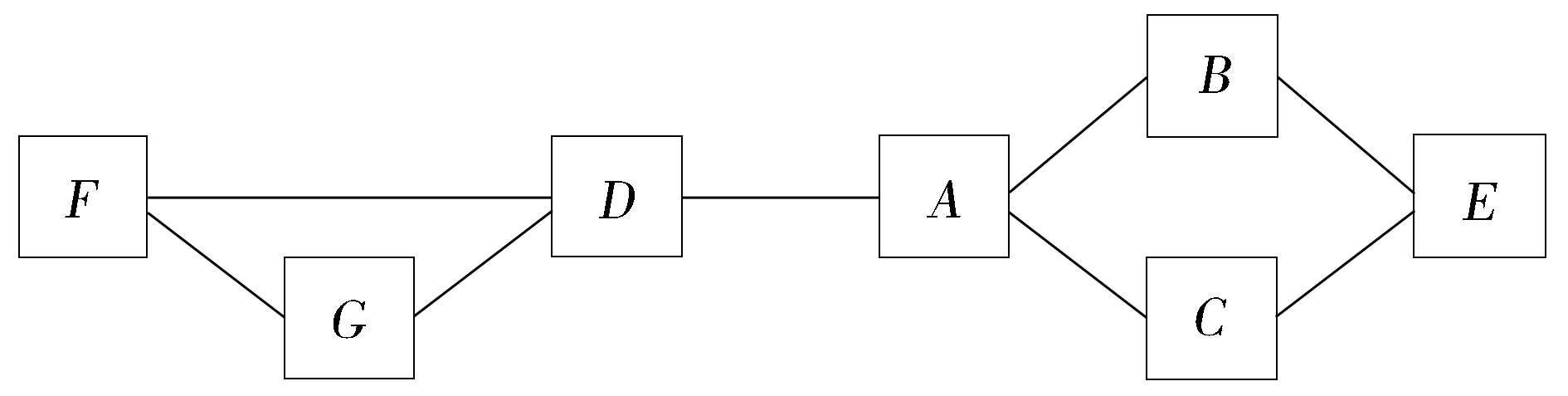
图2 无向图

图模型有不同的类型，主要包括贝叶斯网络、结构方程模型、马尔可夫随机场、隐马尔科夫模型、影响图、社会网络、指令—控制结构等。这些图模型都基于一些基本的图模型结构，例如有向无圈图、无向图、链图、祖先图。现用于认知表征的两类图模型结构是有向无圈图和无向图。其中，有向无圈图简写为DAG，无向图简写为UG。构成DAG的两个条件是：(1)图中只有有向边；(2)没有有向的圈。其中，圈是指从节点X返回到X的路径[4]。图1就是符合这两个条件的DAG。它的有向边可以表征不对称关系，例如A→B。第二种图模型的结构是UG。构成UG的条件是：所有边是无向的。图2就是符合这个条件的UG。UG的无向边表征对称的相关关系。

二、三种类型认知的图模型表征

丹克斯认为，因果认知、基于概念、基于决策的认知等的大多数认知活动可以被图模型表征。

(一)因果认知表征

因果认知是认知的重要组成部分。因果关系是认知中最重要的关系之一。因果知识将独立的事件整合到连贯的因果结构中，使得对世界的认知可以连贯统一。“任何旨在统一多元认知域的理论框架，必须将因果认知作为其中的必要元素。”[2]65

因果关系是一种非对称性关系，即原因产生结果，但结果却不导致原因。DAG基础图模型中的有向边能够表征非对称性关系，例如，C→E的含义是：C造成了E。

丹克斯认为，大部分因果认知可以理解为在同构于DAG基础的图模型的认知表征中的运算。因果认知是对外部世界的因果关系的反映，分为因果推论、因果推理和因果知觉。其中，因果推论和因果推理被图模型表征，构成统一认知的重要组成部分，而因果知觉则不能被图模型表征。

因果认知广义上分为因果学习和因果推理。其中因果学习又可以分为因果推论和因果知觉。因果学习是对新的因果信念的熟悉，因果推理是这些信念多种方式的使用。因果学习更强调过程，有改变表征的含义；而因果推理更强调对结果的应用，有使用表征的含义。因果知觉是对因果关系相对短暂的感知，因果推论指的是从多种情况下推出因果关系的过程[5]。

第一，因果推论被图3所表征。图3是一个DAG基础的图模型，其中，Ci表示原因，E表示影响，wi表示Ci的因果力量，B表示其它存在的不可观察的原因。虚线边指示在每对Ci节点之间可能有边。这即是因果推论的过程，即从一系列没有明确传递出因果信息的例子中学习因果结构。

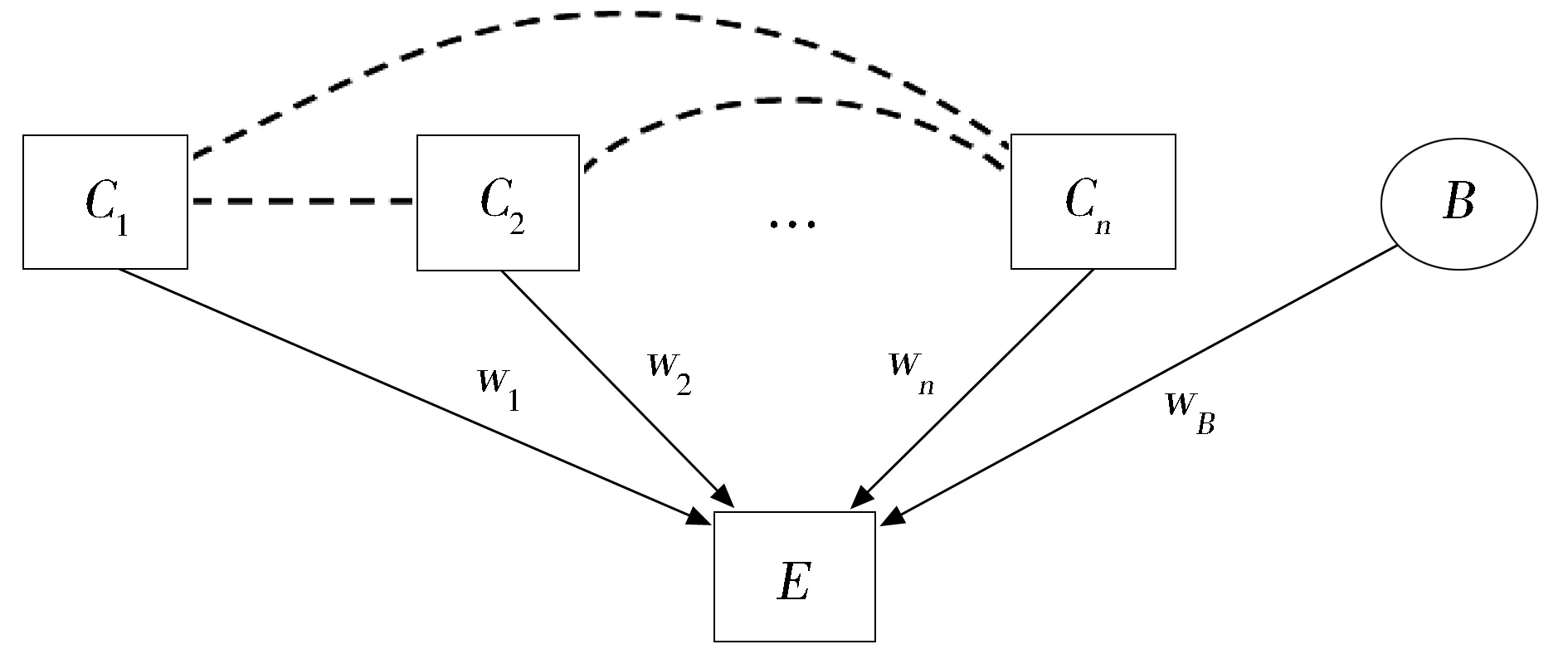
图3 因果推论图[6]359-388

第二，图模型对因果推理进行表征。因果推论是学习因果结构的过程，而因果推理就是应用学习的结果。这些学习结果的图模型基本表征形式是：C→M→E。

第三，因果知觉不能被图模型进行表征。因为因果知觉的表征取决于对象的细微时空细节，而图模型原则上只能应用于相对不连续的现象——离散的因果结构或不同空间地域之间的关系。

综上，除了因果知觉，因果认知中的大部分都可以用图模型表征，并当做图模型的运算。

(二)基于概念的认知表征

概念是认知必不可少的一部分，是认知表征的基本元素。例如，“推翻水杯造成水流”中，包括了“水杯”“水”“推翻”等概念。“认知用概念刻画世界，推论新的个体和对象，分类不同的知识等。”[2]99丹克斯认为，基于概念的认知可被图模型所表征，基于概念的认知是对外部世界的一种反映。基于概念的认知由因果结构概念、样例—基础概念、原型—基础概念三种概念类型所表达。这三种概念类型都被图模型所表征，构成统一认知的一部分。

丹克斯总结了三种用来定义“概念”的理论，分别是：样例—基础理论、原型—理论和理论论。在这三种理论中，概念都被图模型所表征。

第一，样例—基础理论认为，概念是一系列样例的集合，其中，样例作为集合中的成员具有显著性、普遍性和可观察性[7]。样例—基础概念的理论预设是：每一个概念由权威例子的集合所定义，这些权威的例子是普遍可观察的，并成为相关分类的成员。例如，“老虎”这个概念就可以用人类对老虎观察得出的一系列特征来表征。图4为基于特征F的样例—基础概念的图模型，Fi是特征，U是不可观察的原因。在这个DAG的图模型中，每一个Fi取决于一个不可观察的原因。在图模型中引入概率分布，即相似的特征越多，则概率分布值越大，则越符合一个概念。可证明，样例—基础的概念被图4所表征[2]105。

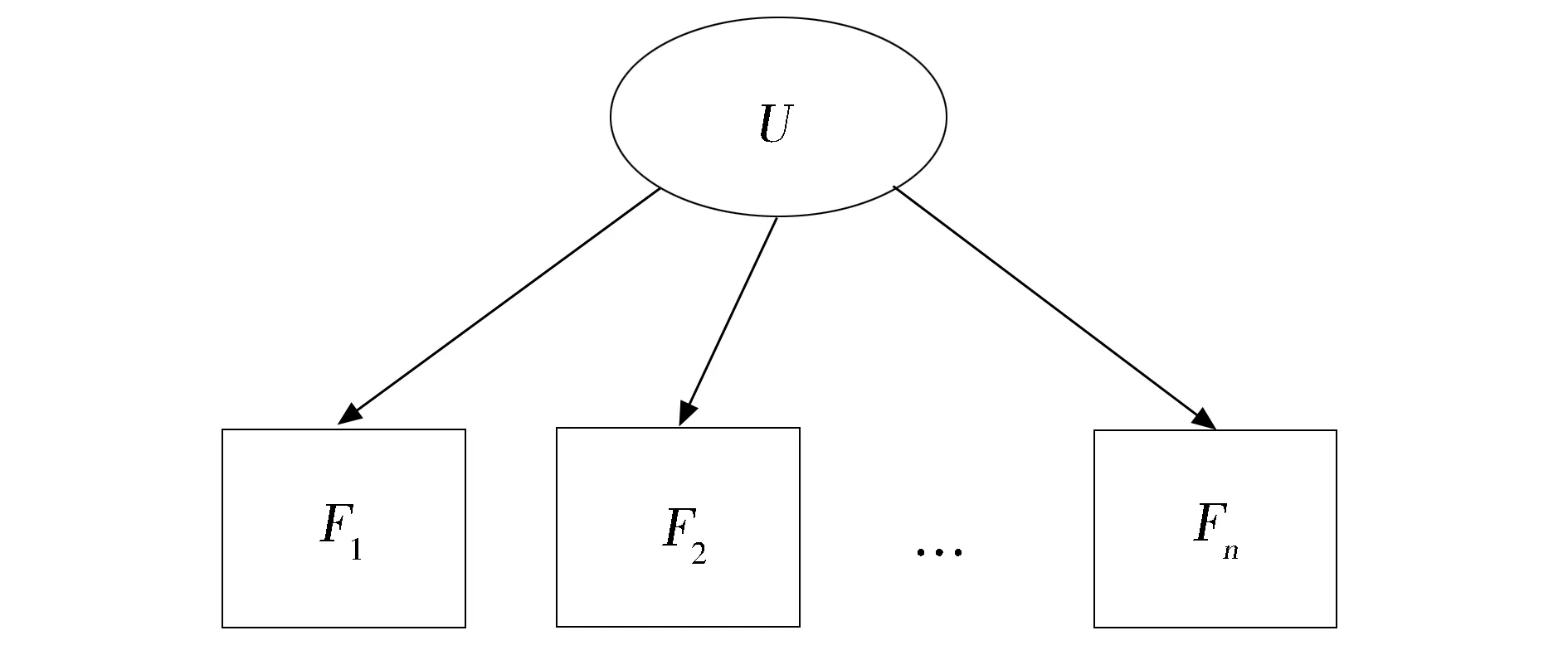
图4 样例—基础概念

第二，原型—理论认为，概念由一些原型的例子所定义[8]。这些原型例子包含了可观察到的例子的总结性信息。与样例不同的是，原型—理论的例子可以不是真实存在的。例如，现实中的鸟是可以飞或者不能飞的，但“鸟”这个概念的原型例子的意义却可以是介于“飞”与“不能飞”之间的。同样引入概率分布，原型基础概念由图5表征[2]106。图5是一个空图，空图既可以被看作DAGs，也可以被看作UGs。

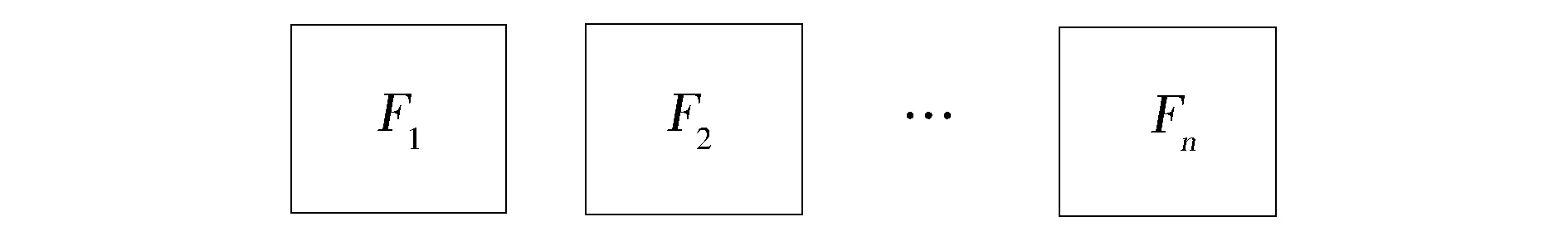
图5 原型—基础概念

第三，理论论认为，概念作为一个理论中的关键术语，是由其在理论结构中的位置所决定的。这种观点认为，概念只有置于广阔的知识结构中才能发挥作用，而不是单独地被定义、阐释。一个典型的说明例子是在因果结构理论中的概念，是被基于因果结构的一致性所决定的。因果结构模型的概念基于因果的DAG模型语言，即因果结构的概念是由因果结构所决定的，而因果结构是由DAG基础的图模型所表征的。

(三)基于决策的认知表征

基于决策的认知既是对外部世界的反映，又能通过行为反作用于外部世界。相对概念和因果认知来说，决策是一种相对复杂的认知过程。因果和概念知识表征本身是不明显的，当它们用于决策的过程时才能发挥其作用。在决策中，因果知识和概念为决策提供了基础。基于决策的认知又由事件、意义、决策行为、决策过程自身四个要素构成，这四个要素及其关系被决定网所表征。

基于决策的认知过程中，四个要素需要用图模型来表征。现今，对决策最有力的图模型表征是决定网[9]。决定网包括四种不同节点类型：(1)世界中的事件或因素，可以用椭圆表示；(2)由决策者实施的行为，可以用长方形表示；(3)意义，可以用菱形表示；(4)决策过程自身，可以用三角形表示。节点意义不同，节点之间的边所蕴含的意义也不一样。事件/因素节点之间的边表示事件之间的因果联系；行为节点之间的边捕捉信息的或认知的联系；意义节点之间的边表示决定决策者在某一刻适时收到的意义的因素；决策节点不需要边。例如，决定是否在一个屋子中开空调，假定决策者想要温度适宜但是不想浪费电。这样一个决策就可以用图6表示。

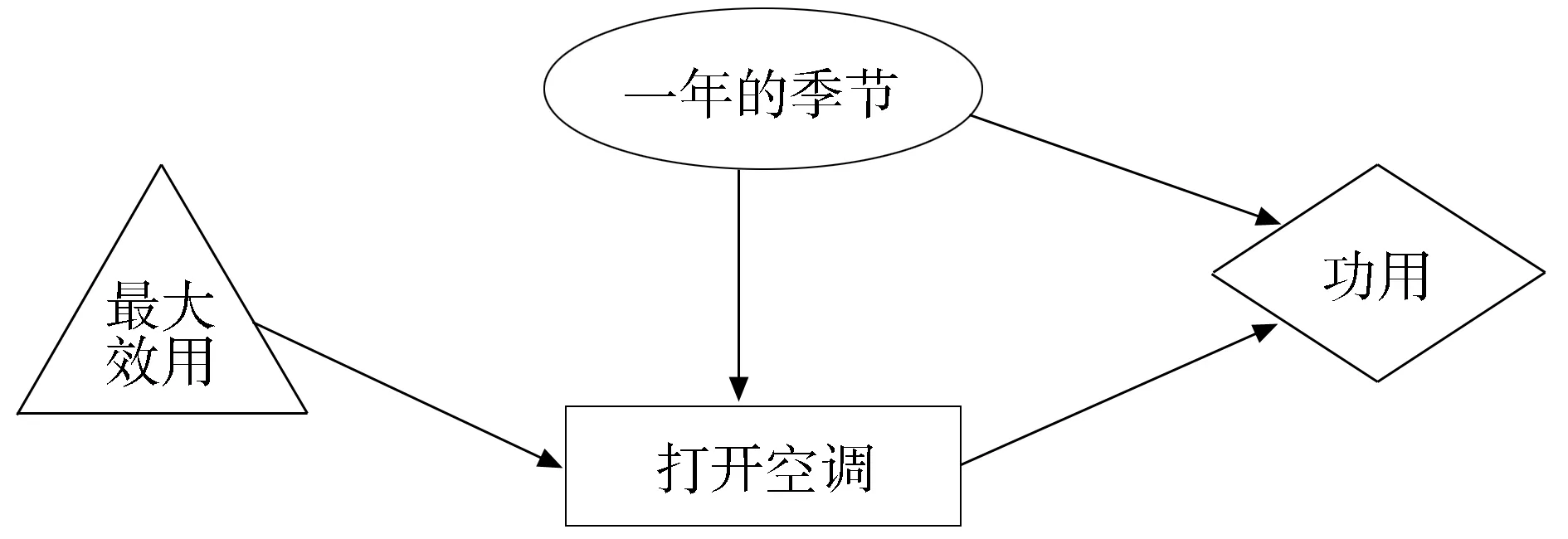
图6 决策图

在图6中，一年的季节编码四季的信息，这个因素明显不在决策者控制范围之内。最大效用表明决策者试图用一个决策过程使得效用最大化；对于或然的决定，指示选择一个行为，这个行为具有产生效用的最大可能。打开空调节点表示决策者真实做出的行为，或者“是”，或者“否”。这个行为是在一年季节的时间信息情况下，由决策程序(最大效用)决定。功用是一年的季节和行为的函数，它的意义取决于：(1)温度适宜；(2)用电的耗费。

三、图模型表征的认知机制

从以上对三种认知过程的语境分析中，我们得知，因果认知、基于概念的认知和基于决策的认知都可被图模型进行表征。丹克斯进一步认为，大量的人类认知活动可以被理解为，在一个结构为图模型的共享表征库中的不同运算。那么，认知表征究竟是通过哪种方式实现共享的呢？认知表征共享的特点是怎样的？对此问题的解释有以下三种：即单库单过程的解释；单库多过程的解释；多库的解释。最终，依据实验数据，丹克斯作出回答：人类的认知是在一个单库单过程的共享表征库中进行的。

单库多过程的解释认为，所有的认知过程都发生在一个共享表征库中，并且多种认知过程可以同时进行。这种解释下的认知的重要特点是处理信息最大化，认知表征信息可以接近最大值，并且可以基本真实地表征外部世界。其计算方式是并行处理计算，因此认知任务和过程对表征结构和内容没有依赖。Brian H.Ross的实验清晰地支持认知任务和过程对表征结构和内容有依赖[2]164。所以，单库多过程的解释不符合人类认知的特征。多库的解释认为，每个认知过程都从不同的库而来，并且，库与库之间没有跨过程的表征共享。这个观点意味着，不同的认知过程之间无法共享表征。例如，从因果学习过程而来的表征将无效于特征推理的过程。York Hagmayer在2010年的实验，以及Bjom Meder、York Hagmayer二人在2009年的实验，证明了在实验中有跨认知翻译发生，所以排除多库的观点[2]162。单库单过程的解释认为，所有的认知过程都发生在一个共享表征库中。在这个表征库中，在任何一个特别的时刻，库中只有很少的认知过程是活跃的。在不同认知转换过程中，有大量跨认知翻译的发生。跨认知翻译的介入，使得多元过程在时间中有序地发生彼此间转换，不是同时性地改变。在单库单过程的解释中，认知任务和过程对表征结构和内容有依赖。2009年Bob Rehder，Robert M.Colner和Aaron B.Hoffman的眼睛追踪数据实验和Sarah Wellen关于目标依赖实验为单库单过程提供直接证据。此外，Wiliam Nichols和丹克斯在2007年一系列实验同单库单过程解释最为匹配[10]。所以，人类的认知更符合单库单过程的解释。

综上，一个良好的认知构架具有以下条件：(1)仅有一个表征库；(2)认知表征的结构是图模型；(3)一个时刻仅有一个认知过程建模表征；(4)在表征学习期间，跨认知翻译展现出依赖于任务和目标的可预料的模型。由此，符合这四个条件的认知构架便能够实现统一认知的理论目标。

四、图模型表征的方法论意义

丹克斯以图模型为工具，对因果认知、基于概念的和基于决策的认知进行表征，并将它们统一于单库单过程的共享表征库中，以此完成认知统一的理论构建，这对于认知科学的哲学研究具有深刻的方法论启迪。

第一，丹克斯的图模型认知表征丰富完善了认知统一理论，为解释心灵的统一性开辟了新的进路。通过上文分析，可以看到图模型认知表征框架具有统一性。丹克斯的图模型认知表征理论通过解释不同认知过程之间无缝转换来构建认知的统一性。“我们可以在认知过程和表征之间轻易移动，并且不同类型的认知似乎轻易地分享信息。”[2]1丹克斯认为，不同类型的认知过程发生在一个单库单过程的认知表征库中，认知之间存在着跨认知翻译，并且随着时间变化实现到另一种认知类型的转化。

第二，丹克斯的图模型认知表征作为计算表征主义的一种辩护和推进，为认知科学提供了新的计算主义的方法论。它把认知当做对信息的编码和计算，在本体论上站在表征实在论的立场，在方法论上坚持了计算主义。它的计算工具是图模型。图模型具有精确计算的特征，用它来表征认知解释了现实世界中认知的精确性特征。通过第一部分关于图模型的讨论我们知道，图模型因其模块化的特征而具有精确计算的能力。在对认知表征的计算过程中，只需推理、计算相邻节点，而不需考虑更多无关因素。总之，图模型作为一种可以精确计算的数学工具，可以合理、有效地表征并整合认知研究。

第三，丹克斯的图模型认知表征理论具体构建过程中运用了隐喻的方法。在对认知的研究上，丹克斯用系统模型方法试图构建认知模型[11]。“认知模型是基于观察和推理、能够描述认知方向、储存和使用信息的隐喻。”[12]一些关于记忆的理论用了“库隐喻”[13]，认为人的记忆储存在大脑某个部位，就像把东西存在仓库中一样。丹克斯的图模型认知表征理论将库隐喻应用于认知统一的研究，认为不同的认知过程共同发生在共享表征库中。与以往“库隐喻”不同的是，丹克斯的共享表征库的结构是图模型，内容是不同的认知过程，特点是单库单过程，同时兼顾了表征和过程两个维度。

此外，图模型对认知的表征，可以描述、预测、解释人的行为，也就使得它在实践上具有应用于人工智能领域的可能性。丹克斯的图模型认知表征理论为人工智能对因果认知、基于概念和决策的认知表征和模拟提供了一套算法体系。图模型理论被广泛应用于社会经济、工程技术与管理等领域，图模型对于认知的表征拓展了图模型理论的应用空间。

总之，图模型用于认知科学的研究已经取得了丰硕的成果。丹克斯的图模型表征理论丰富完善了认知统一理论，并为认知科学提出新的计算主义方法。不过，图模型认知表征理论也遭遇许多挑战，例如，它不能表征因果知觉；丹克斯的图模型认知理论与福多的模块性理论有冲突，因为他的图模型认知理论旨在以表征为中心统一认知，认为认知发生在一个单库单过程的共享表征库中，而福多式模块化假定人的认知划分为基于过程的模块；图模型认知表征理论暂时缺乏神经科学的证据。面对这些挑战，图模型认知表征理论还需完善。

[1] 唐孝威.统一框架下的心理学与认知理论[M].上海：上海人民出版社，2007：170.

[2] Danks,D.Unifying the Mind——Cognitive Representations as Graphical Models[M].Cambridge:The MIT Press,2014.

[3] 罗姆·哈瑞.认知科学哲学导论[M].魏屹东,译.上海：上海科技教育出版社，2006.

[4] Daphne Koller.概率图模型原理与技术[M].王飞跃，韩素青，译.北京：清华大学出版社，2015：36.

[5] Rips,L.J.Causation from perception[J]. Perspectives on Psychological Science,2011，6:77-97.

[6] Danks,D.Causal learning from observations and manipulations[A],M. C. Lovett, P.Shah.Thinking with data[C],Mahwah,NJ:Erlbaum,2007:359-388.

[7] Logan,G.D.Cumulative progress in formal theories of attention[J].Annual Review of Psychology,2004，55:207-234.

[8] Minda,J. P.,Smith,J.D.Prototypes in category learning: The effects of category size,category structure,and stimulus complexity[J]. Journal of Experimental Psychology: Learning, Memory, and Cognition,2001,27:775-799.

[9] Shachter,R.D.Evaluating influence diagrams[J].Operations Research,1986,34:871-872.

[10] Nichols,W.,Danks,D.Decision making using learned causal structures[A], D.S.McNamara,J.G.Trafton.Proceedings of the 29th Annual Meeting of the Cognitive Science Society [C],Austin,TX: Cognitive Science Society,2007,1343-1348.

[11] 魏屹东.广义语境中的科学[M].北京：科学出版社，2004：58.

[12] 魏屹东.认知表征的方法论：隐喻、假设与建模[J].山西大学学报(哲学社会科学版)，2009，32(5)：24-28.

[13] 魏屹东.认知科学哲学问题研究[M].北京：科学出版社，2008：116.