融合PSO与DE的认知决策引擎

张煜培 赵知劲， 郑仕链

(1. 杭州电子科技大学浙江省数据存储传输及应用技术研究重点实验室，浙江杭州 310018；2. 中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室，浙江嘉兴 314001)

1 引言

认知无线电需要感知外部无线信道环境，并根据信道条件、用户需求和其他信息等优化决策传输参数，以充分利用有限的频谱资源[1]。因此，如何根据当前通信场景自适应调整传输参数是实现认知无线电的一个关键问题。

根据环境参数，其包括路径衰落、噪声功率、功率消耗、频谱效率、频带干扰等，自适应调整传输参数[2]，包括发射功率、调制类型、调制指数、带宽、编码速率、帧长、时分双工和吞吐量等。期望优化的目标通常有最小化误比特率(bit error rate， BER)、最小化功率消耗、最小化干扰、最大化数据吞吐率、高QoS、最大化频谱效率等。如果同时优化多个指标，系统复杂度会大幅增加；并且以上目标之间存在依赖性和竞争性的关系。例如，增加调制指数可以增加数据速率，但是同时会增大BER；为了减小误帧率(frame error rate， FER)，需要降低符号率和调制指数，但是会降低速率。因此自适应参数调整过程是一个多目标优化过程。认知决策引擎(cognitive decision engine，CDE)解决参数最优化问题。

智能优化算法仅仅依靠适应度值估计解的质量，并通过当前搜索的最优解去寻找全局最优解，已在CDE中得到应用[3-11]。文献[4]用遗传算法(GA)解决认知决策引擎；文献[5]利用了量子遗传算法(QGA)，采用量子比特编码，通过量子门更新，与GA相比，收敛速度和收敛精度有很大提升；文献[6]和文献[7]分别采用二进制粒子群(BPSO)和爬山遗传(HGA)算法；文献[8]和文献[9]分别提出量子粒子群算法(BQPSO)和混沌粒子群算法(BCPSO)，证明比BPSO更有效；文献[10]提出协进化粒子群算法(CPSO)，文献[11]提出基于差分进化(DE)算法，整体优化性能优于文献[10]的CPSO。

但以上算法未考虑带宽、编码速率、帧长和时分双工等传输参数，且在参数寻优的收敛速度和精度上有待进一步提高，因此本文提出5个目标函数优化的改进IPSO-DE算法，充分利用网络资源以实现全局性能的最优化。

2 认知决策引擎

为了更好地满足用户需求和外部环境变化，认知无线电需要调整自身参数来优化系统性能，在多变的无线环境下实现期望的QoS。认知决策引擎就是要实现认知无线电适应性参数调整功能。

2.1 认知决策引擎建模

图1给出了认知决策引擎结构图，其中作为决策CDE需要收集用户需求、政策域和频谱可用性等信息，使其与无线通信环境相适应，从而使系统能够满足各种业务需要[12]。一般认知引擎需要调整n个决策变量并优化m个目标函数。不同的链路条件和用户需求会对不同的目标函数有所侧重。本文综合考虑各种传输参数，设计了如下5个目标函数。

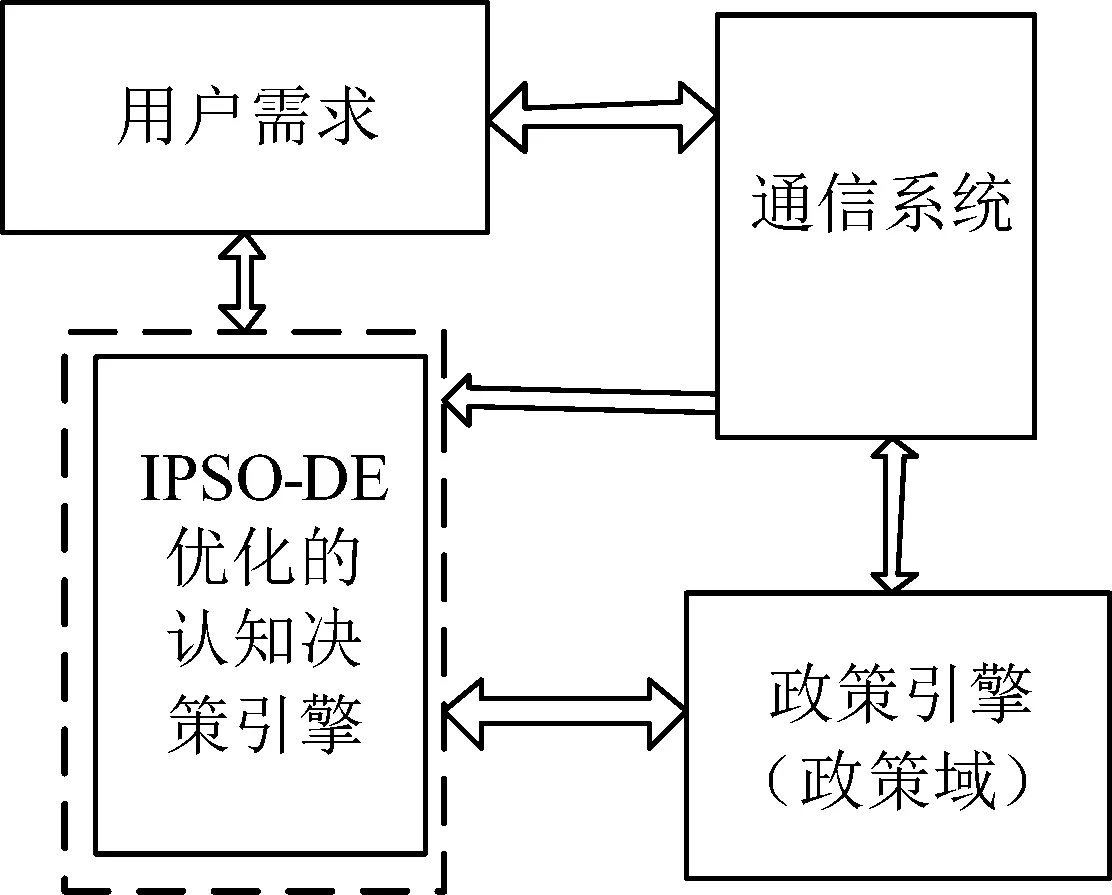
图1 认知决策引擎结构图

(1)最小化平均发射功率

在认知无线电应用中，认知设备需要持续在低功耗模式下工作，例如在紧急通信中，设备需要利用有限的能量持续工作。其中发射功率、信道带宽、符号速率和调制类型对功耗都有影响[3]。本文只考虑发射功率的影响，定义归一化平均发射功率如下：

(1)

其中，Pwi是第i个子载波的发射功率，Pwmax是最大功耗，N是载波总数。

(2)最小化误比特率

误比特率是衡量通信质量好坏的一个重要指标，其与信道类型、调制阶数和SNR都有关。在加性高斯白噪声信道中，MPSK和MQAM的BER分别定义为[3-5]：

(2)

(3)

其中，M是调制阶数；Q(·)是误差函数如式(4)所定义

(4)

γ是接收信噪比。通常用Eb/N0表示γ，Eb和N0分别是每比特信号能量和噪声功率谱密度，Eb由接收信号功率S、码率Rs和调制阶数M决定。

在多载波系统中，假设子载波最差BER为0.5，第i个子载波的BER为Pei，因此归一化的BER定义为：

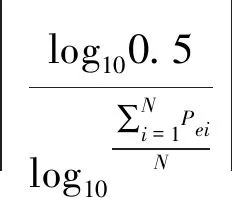
(5)

(3)最大化吞吐率

在认知无线电环境中，当需要提供多媒体或者视频服务时，最大化吞吐率比最小化传输功率重要。链路吞吐能力代表单位时间内传输的有效数据量。归一化的数据吞吐率定义为[6- 8]：

(6)

其中，Mi是第i个子载波的调制指数，Mmax是最大的调制阶数。当所有子载波用最大调制阶数时,fmax_throughtput为1。

(4)最小化频谱干扰

认知用户分享主用户的频谱资源，所有认知用户都必须避免对主用户和其他认知用户造成干扰。因此，频谱干扰是衡量认知无线电的一个重要指标。本文使用传输功率和带宽之积定义频谱干扰[3]：

finter=Pw·BW

(7)

随着功率和带宽的增加，认知用户的干扰也会增加，在多载波系统中，归一化的频谱干扰定义如下：

(8)

其中，Pwi和BWi分别是第i个子载波的功率和带宽，Pwmax和BWmax分别是最大的传输功率和最大化传输带宽，Pwmin和BWmin分别是最小的传输功率和最小化传输带宽，TDDi是第i个载波的时分双工占比。

(5)最大化频谱效率

认知无线电主要目的是提高频谱利用率，它代表在有限频带上传输数据的能力，系统带宽、符号速率和调制类型都对其有影响，频谱效率定义为：

(9)

其中，Rsi是第i个子载波符号速率，Rsmax是最大的符号速率。

我们希望fmin_power、fmin_ber和fmin_inter越小越好,fmax_throughtput和fmax_spec越大越好。但这5个目标函数相互影响。CR引擎尽可能优化以上目标函数，得到最优参数解。

为了简化要解决的问题，对所有目标函数进行归一化，从而保证所有目标函数值置于[0，1]之间。假设归一化的目标函数为f=[f1,f2，…,fm]，将多目标优化问题可以转换成单目标函数：

(10)

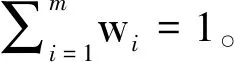
fit=w1(1-fmin_ power)+w2(1-fmin_ber)+w3fmax_throughtput+

w4(1-fmin_inter)+w5fmax_spec

(11)

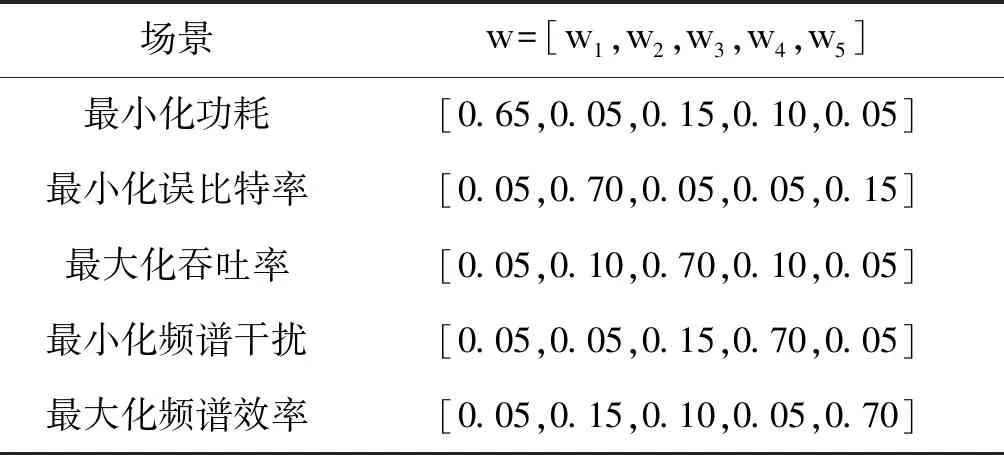
表1 权重值

3 融合PSO与DE的认知决策引擎

为了兼顾用户QoS和实时性需求，对算法的求解速度及求解精度有较高要求，智能优化算法因其具有高效的随机搜索能力被视为解决CDE的有效途径。

3.1 二进制粒子群算法

二进制粒子群算法(BPSO)可用于解决离散优化问题，在迭代过程中，每个粒子都在搜索可能解。它们根据式(12)和式(13)更新速度vi=(νi1，νi2，…，xiD)和位置xi=(xi1，xi2，…，xiD)，D是搜索空间维度，νij和xij分别表示第i个粒子第j维的速度和位置。

(12)

(13)

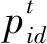
3.2 二进制差分进化算法

差分进化的DE/best/1/bin形式[14]主要步骤如下。

随机选择两个个体xr1和xr2，将二者的加权差加到全局最优解g上，产生新的变异个体v。

v=g+(-1)sig|xr1-xr2|

(14)

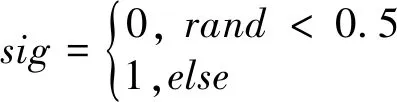
(15)

然后将变异向量按式(16)进行交叉，得到交叉个体u。

(16)

其中CR为交叉概率，通常设置为常数，rand为[0，1]上的随机数，randn(D)为随机产生的[1，D]上的整数。为了决定交叉个体是否成为下一代个体，按照贪婪准则将ui和xi比较，按照式(17)确定下一代种群。

(17)

3.3 融合PSO与DE的认知决策引擎

粒子群算法中的we衡量了前一时刻的速度对当前速度的影响[15]，用于平衡算法的局部搜索能力和全局搜索能力，本文提出一种按照个体适应度值的惯性权重we进行自适应调整策略。首先定义相似度函数为：

(18)

其中Hamming(xi，xj)表示xi，xj的海明距离。然后以当前种群中最差个体xmin为衡量标准，定义惯性权重为：

(19)

由于粒子群算法容易陷入局部最优，而差分进化算法具有良好的全局寻优能力，本文对适应度值较低个体利用差分进化算法进行优化变异，增加粒子群个体的差异性。即在每次迭代过程中，设定平均适应度值作为门限，将低于门限的个体通过全局搜索能力强的差分进化进行优化。同时提出式(20)所示的自适应交叉概率，代替式(16)中的交叉概率，其根据每个个体xi的适应度值决定第i个个体的交叉概率，适应度值小的个体具有较大的交叉概率，以快速淘汰当前劣解，寻找更优解。

CRi=fitmax-(fitavg-fit(xi))·e-(fitmax-fitmin)/4

(20)

其中fitmax、 fitavg和fitmin分别表示最优个体适应度值，平均适应度值和最劣适应度值。由此得到本文提出的改进粒子群(IPSO-DE)算法将其应用于本文的参数优化决策，得到本文提出的融合PSO与DE的认知决策引擎算法(仍记为IPSO-DE)，其主要步骤如下：

(1)初始化：产生种群大小为N的种群。设置迭代次数I和间隔代数T，令t=1。

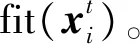
(3)更新个体：利用式(18)～(19)计算第i个个体的惯性权重wei，利用式(12)～(13)对个体的速度和位置进行更新，计算平均适应度值fitavg；

(4)种群划分：将适应度值高于fitavg的个体归入种群Popt中，其余归入Pwor。

(5)进化劣质个体：对Pwor中个体按照式(14)～(15)进行变异，按照式(20)确定每个个体的交叉概率CRi、再按照式(16)进行交叉，最后按照式(17)进行选择。

(6)将经过差分进化优化后的个体和种群Popt合并，并确定全局最优个体gt。

(7)判断t≤I是否成立，若成立，t=t+1，转步骤(2)；否则转步骤(8)。

(8)输出gt，将其解码，完成参数配置。

4 算法仿真与性能分析

本节仿真分析比较本文提出的IPSO-DE与HGA[7]、BQPSO[8]、BCPSO[9]算法对多载波系统参数的认知决策性能。

4.1 参数设置

多载波系统具有32个子载波，每个子载波分配一个[0，1]上均匀分布随机的数以模拟信道衰落情况。发射功率为0～25.2 dBm，步进为0.4 dBm，共有64种选择，用6位二进制bit编码。数据率设置为1 Mbps。调制方式包括BPSK、QPSK、16QAM、32QAM、64QAM、128QAM和256QAM共7种，编号为1至7，由3位二进制bit编码。信道带宽为2～32 MHz，步进为2 MHz，用4位二进制比特编码。TDD为25%～100%，间隔为25%，由2位二进制bit编码，码率为125～1000 Ksps，步进为125 Ksps，用3位二进制bit编码，整个系统需要576 bit，寻优空间为2576。背景噪声为加性高斯白噪声，噪声功率为-80 dBm，路径损耗为85 dB。HGA[7]、BQPSO[8]、BCPSO[9]和本文的IPSO-DE算法中设置种群规模P=30，迭代次数I=1500；HGA的交叉概率为0.6，变异概率为0.001。BCPSO的控制参数μ为4。

按照公式(11)和表1分别设计的目标函数和权重值，求得的四种算法在最小化功耗、最小化BER、最大化吞吐率、最小化频谱干扰和最大化频谱效率模式下适应度曲线如图2～6所示，每条曲线都是10次独立实验的平均。从图2～6可知，随着进化代数的增加，平均目标函数总体趋势增大，算法终止时所获得的目标函数值要明显高于进化初期的目标函数值，从而验证了四种算法调整认知无线电参数的有效性。在五种模式下，本文提出的IPSO-DE算法的平均目标函数值均高于其他三种算法，说明该方法具有较好的寻优性能，该算法还能兼顾探索和开发的能力。同时可以看出BQPSO算法在模式2下表现较差，HGA算法在模式5下表现较差，BCPSO在模式2和模式5下均表现较差，说明这三种算法对参数较为敏感。

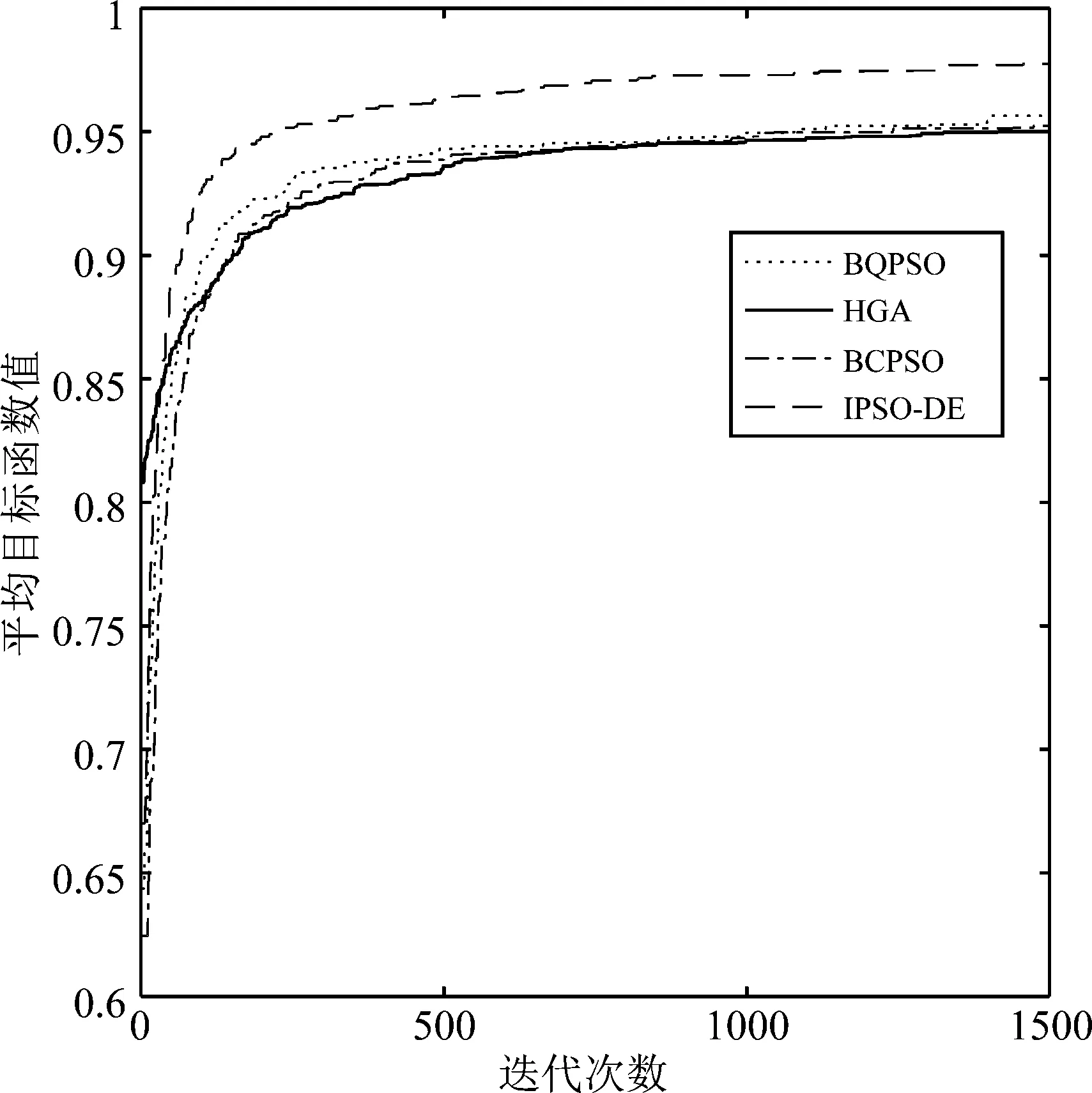
图2 最小化平均发射功率下目标函数值曲线

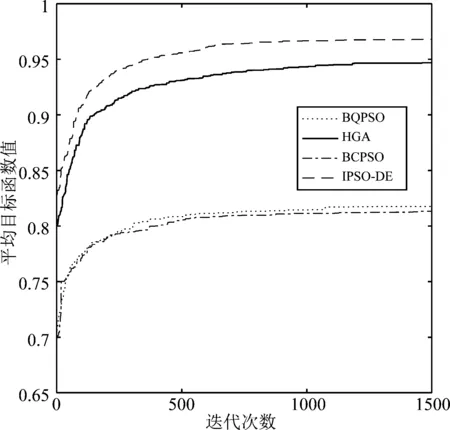
图3 最小化BER下目标函数值曲线

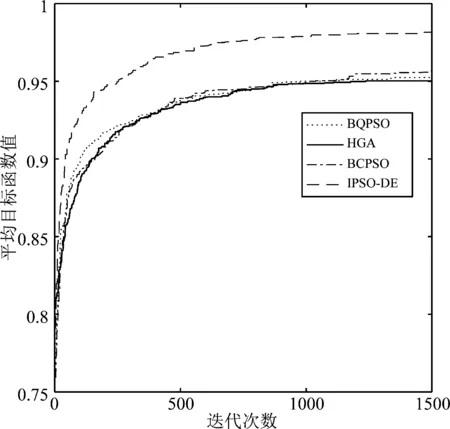
图4 最大化吞吐率下目标函数值曲线

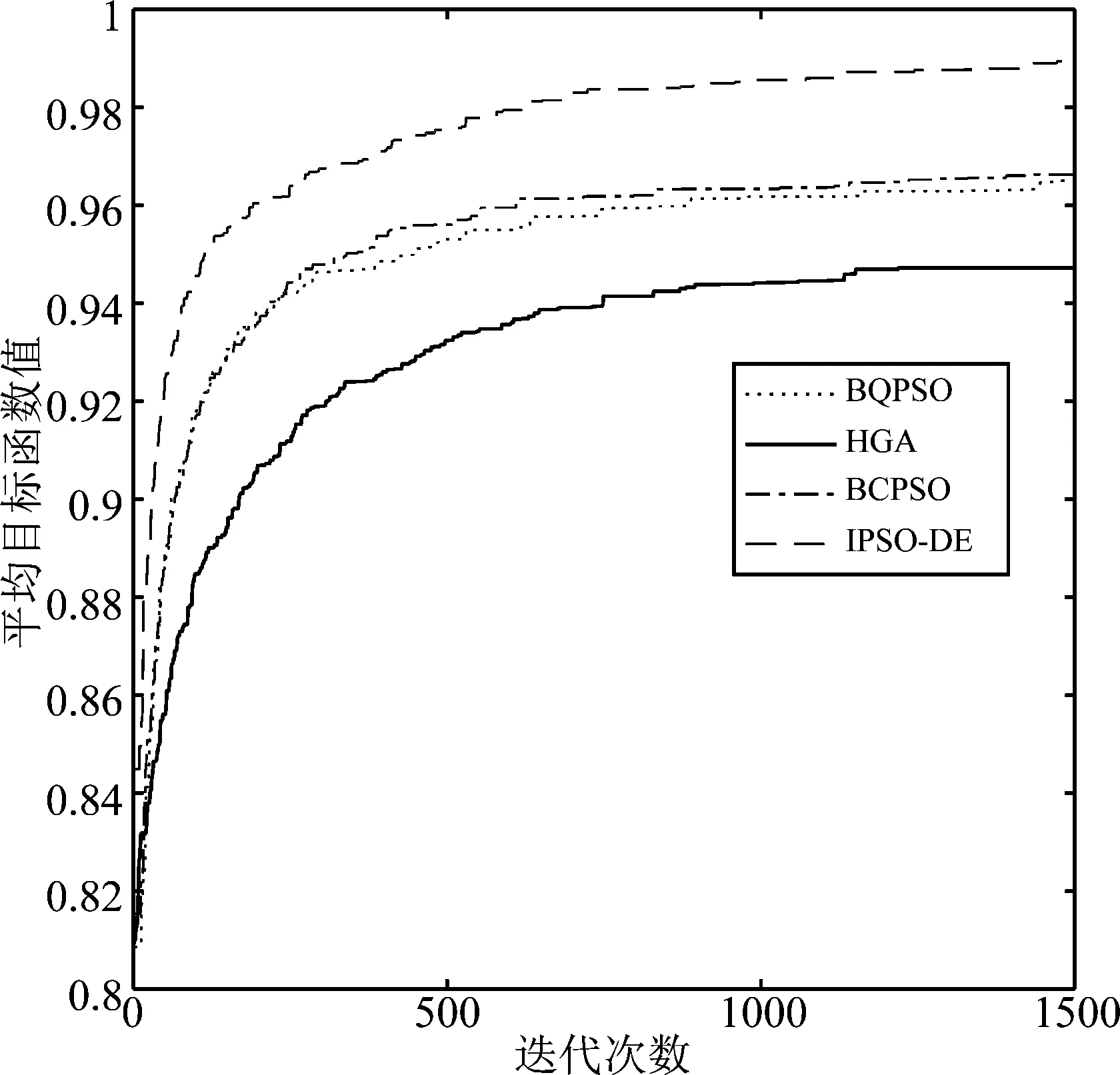
图5 最小化频谱干扰下目标函数值曲线

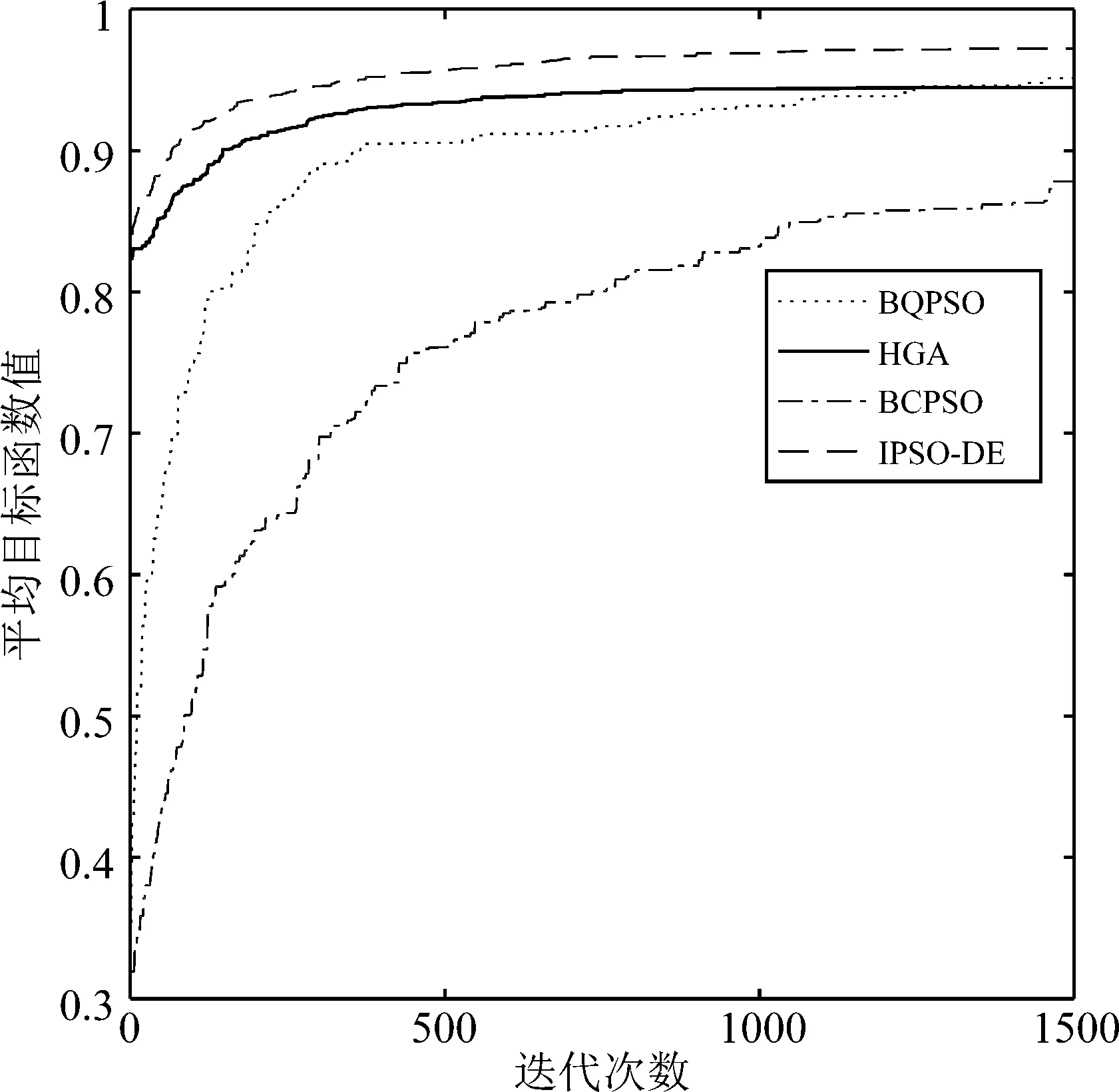
图6 最大化频谱效率下目标函数值曲线

图7～11给出了本文IPSO-DE算法在最小化平均发射功率、最小化BER、最大化吞吐率、最小化频谱干扰和最大化频谱效率模式下的参数配置。图7中，平均发射功率为0.1 dBm，说明该算法成功实现了场景1下对最小化发射功率这一主要目标函数优化，同时也兼顾了其他四个目标函数的要求。图8中，误比特率为1.86×10-4，调制方式基本为BPSK和QPSK，这种方式实现了低BER。图9中调制方式基本上调整为256QAM，实现了最大化吞吐率。图10中具有较小的TDD、Pw和BW，实现了最小化干扰的目标。图11中具有较大的M、Rs和较小的BW，实现了最大化频谱利用率这一目标。

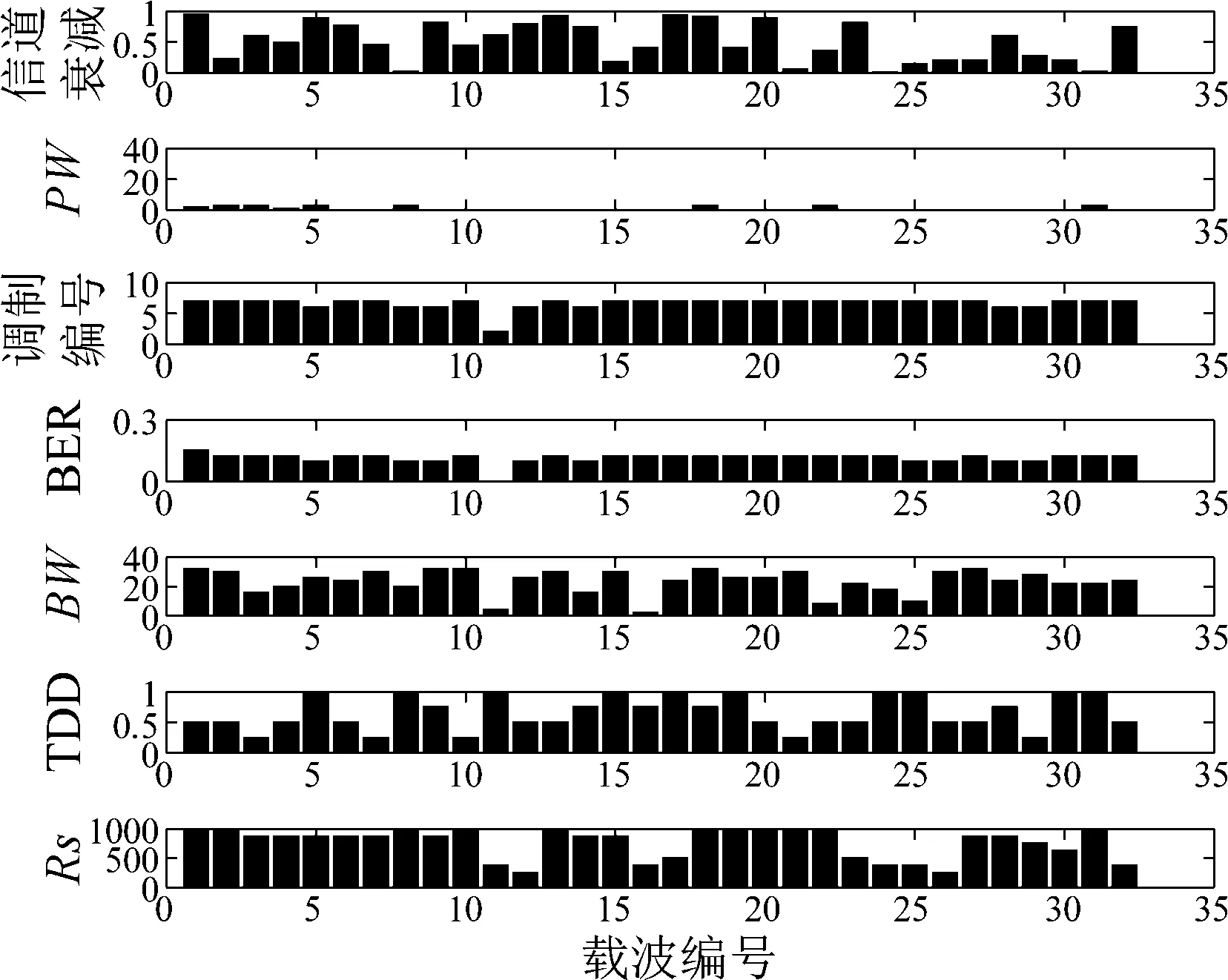
图7 最小化平均发射功率下参数调整

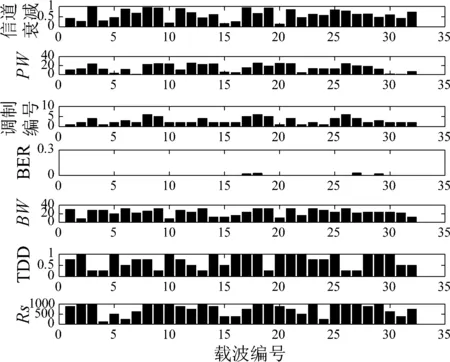
图8 最小化BER下参数调整

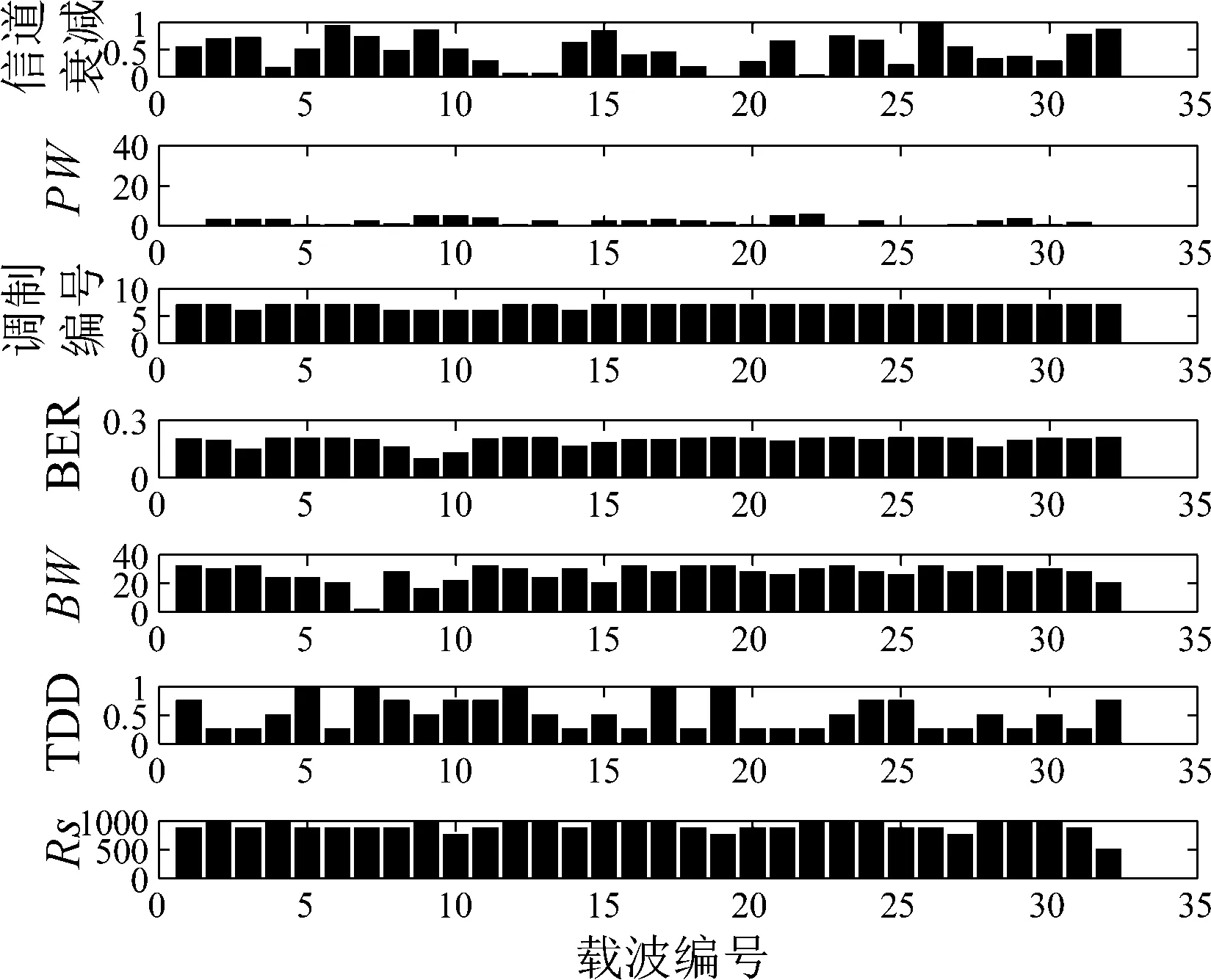
图9 最大化吞吐率下参数调整

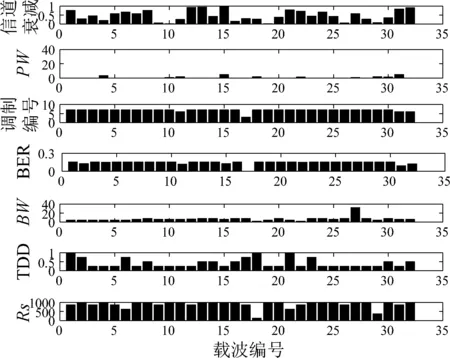
图10 最小化频谱干扰下参数调整

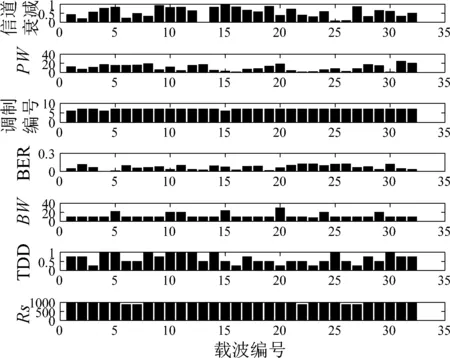
图11 最大化频谱效率下参数调整

5 结论

在认知无线电系统中，认知用户需要在不干扰主用户前提下动态使用频谱空穴，并且根据复杂多变的信道环境实时优化传输参数。本文提出利用5个目标函数的优化模型，该模型充分考虑无线通信各种传输参数，以网络整体性能最优为目标。为了提高利用PSO算法求解CDE问题的收敛速度和收敛精度，IPSO-DE算法改进了惯性权重，利用DE进化粒子群劣等群体，并改进了DE的交叉概率更新方式，增强了种群的探索能力。多载波系统的仿真结果表明IPSO-DE算法寻优能力强、收敛快、准确性高。