基于仿射变换的胶囊网络特征研究

付家慧 吴晓富 张索非

(1. 南京邮电大学通信与信息工程学院，江苏南京 210003； 2. 南京邮电大学物联网学院，江苏南京 210003)

1 引言

目前，图像中目标识别的方法大都借助于卷积神经网络[1- 4]。这种方法能够在不知道确切位置的情况下正确识别目标并实现分类。 CNN应用到图像识别上似乎非常合理，而且实际表现也非常好，但是神经网络的创始人之一Hinton认为CNN中的池化操作是一个灾难，因为池化过程在一定程度上弱化了神经网络结构对于位置信息的准确把握。允许模型对一些小的空间上的变化视而不见，并不能精准地学习到不同物体的位置关联。比如在面部识别中，需要一个鼻子和一张嘴这样的高层部分之间精确的空间关系的知识[5]。但在卷积网络中进行了多次下采样后，在它们的姿态中，高层特征就有了很大的不确定性。如果此时把人脸照片中的一只眼睛与嘴巴的位置对调一下，CNN还是会将其识别成人脸，这显然是不对的。

所以对于卷积神经网络而言，识别空间位置关系的能力是十分有限的，不仅如此，CNN对于旋转图像的识别能力也是有限的，当神经网络模型训练完成后，对测试集上的图片做不同角度的旋转处理，最后得到的准确率相较于不做旋转处理的数据集会明显降低。所以旋转之后的人脸图像会存在极大的概率被错判。

人类识别图片是基于平移和旋转将看到的图片与大脑中已存在的图片模式进行匹配，但是这个对于CNN来说是有一定困难的，为了解决这个问题，G.E.Hinton最先在2011年提出了Capsule Network的模型[6-7]，该模型不再以“神经元”激活中的视角不变性为目标。而是使用局部“胶囊(capsules)”，这些“胶囊”对输入进行一系列复杂的内部操作，然后把计算结果封装成一个高信息量的信息输出的小向量。在一个有限的观察条件和形变的领域，每个胶囊学习识别一个隐式定义的视觉实体，它的输出可以是实体出现在有限领域内的概率，也可以是一些包括视觉实体正确的姿态、光照和形变等信息的“实例化参数”。

为了更好的理解胶囊网络较卷积神经网络在识别空间位置信息上的优势所在，本文研究了平移、旋转等基础仿射变换下的胶囊网络特征的可视化问题。论证得出胶囊网络的确可以通过内部集成的胶囊模块去学习和输出包括视觉实体正确的姿态、形变等信息在内的“实例化参数”。同时为验证在平移、旋转过程中的实验结果准确性，论文中给出了数字识别的评价指标，并对每一个仿射变换的实验过程给出了识别准确性的评价。

2 仿射变换下胶囊网络及卷积网络特征可视化

2.1 平移变换下的胶囊网络特征可视化

2.1.1 胶囊网络的平移模型

图1中的网络模型为G.E.Hinton在2011年提出的平移Capsule Netwot网络模型。整个模型由多个分立结构的模块组成，我们称之为“胶囊模块”。

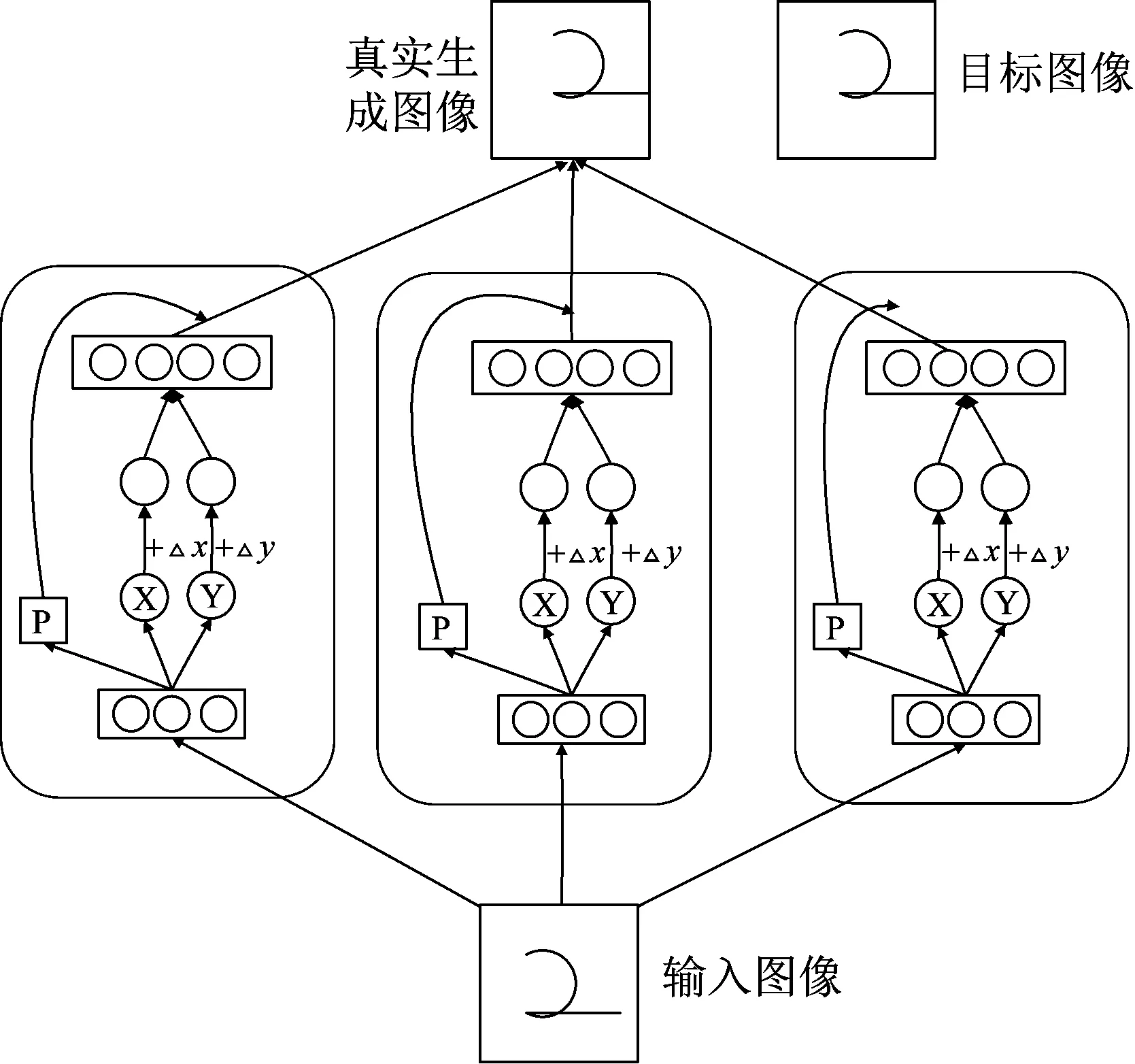
图1 基于胶囊网络的平移模型

图中的网络模型由三个胶囊模块组成，每个胶囊模块的内部网络结构相同，由三个识别单元和四个生成单元组成。识别单元旨在将图片的像素强度信息转换为位置关系信息，X、Y、P是识别单元的输出值，分别表示图片中的位置关系信息以及胶囊的视觉实体在输入图像中存在的概率。△x、△y分别表示二维图像在横轴和纵轴的偏移量，由学习到的位置关系信息加上偏移量得到的位置信息做生成单元的输入，最后又得到了由位置关系信息转换而来的像素信息，最后得到的真实图像是各胶囊模块与其对应的概率p加权和的结果。

2.1.2 平移变换下的网络特征可视化的实现过程

平移胶囊网络的实现基于MNIST数据集，预处理过程利用python的roll函数对所有的数字图像在x、y坐标轴做-5到5范围内任意大小的平移。

具体胶囊模块的网络的搭建仿照图1的平移模型。网络的搭建基于全连接层，逻辑识别单元层的尺寸为784×10，逻辑生成单元层的尺寸为2×20。主要的训练参数如表1所示。

表1 平移胶囊网络主要训练参数

对比传统的可视化方法[8-9]，利用 Tensorboard的可视化效果更理想。在平移模型中主要对平移过程中的loss函数、各胶囊模块的输出特征图像、预处理前后的是数字图像以及生成的真实图像进行可视化，另外，本文为探究胶囊网络对于位置信息的学习性，将逻辑识别单元的输出概率p和二维坐标值进行激活输出，并于Matlab中进行可视化处理。

2.2 旋转变换下的胶囊网络特征可视化

2.2.1 胶囊网络的旋转模型

胶囊网络的旋转模型如图2所示，逻辑识别层、逻辑生成层以及概率值p的目的与平移模型中的相同，不同的是为实现对任意角度旋转图像的学习，利用了图像矩阵绕中心点旋转的矩阵运算式(1)：

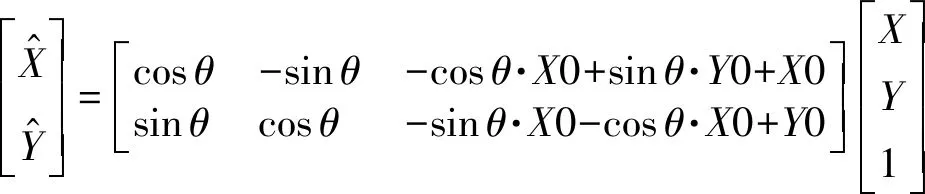
(1)

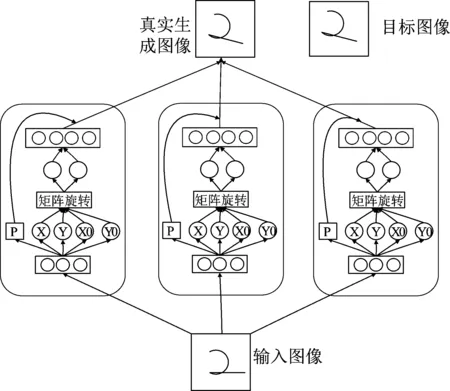
图2 基于胶囊网络的旋转模型

除此之外，与平移网络模型最大的不同在于对于图像中心点X0、Y0的定义也是通过学习来得到的，即每一个胶囊都有自己独立学习到的X0、Y0。胶囊网络最后得到的真实图像仍旧是各胶囊模块与其对应的概率p加权和再做激活的结果。

2.2.2 旋转变换下的网络特征可视化的实现过程

旋转胶囊网络的实现基于MNIST数据集，利用opencv对所有的数字图像在中心点处做-180°到180°的任意角度旋转。胶囊网络的搭建仿照图2的旋转模型。逻辑识别层与逻辑生成层的尺寸与平移模型中的相同。主要的训练参数如表2所示。

表2 旋转胶囊网络主要训练参数

同样的，在旋转模型中对预处理前后的手写体图像、生成的真实图像、各胶囊模块的输出特征图像以及激活前的输出像素矩阵进行可视化，与此同时，将逻辑识别单元的输出概率p、旋转前后的位置坐标以及中心位置坐标进行可视化处理。

2.3 固定旋转中心下的胶囊网络特征可视化

2.3.1 胶囊网络的旋转模型

基于胶囊网络的固定中心点的旋转模型如图3所示，由上一节的内容可知，基于胶囊网络的旋转模型具有很好的健壮性，在一个相对分散的中心点的情况下，依旧可以很好的生成接近于目标图像的真实图像，为探究固定中心点时的网络效果及位置关系，对图2中的基于胶囊网络的旋转模型做一些结构上的改变，如图3所示，改变了模型自身的分立性和封闭性，除了在最后一层相连以外，令其余多个胶囊模块共用第一个胶囊模块学到的中点位置信息，其余结构与原网络一样，在这里不做赘述。

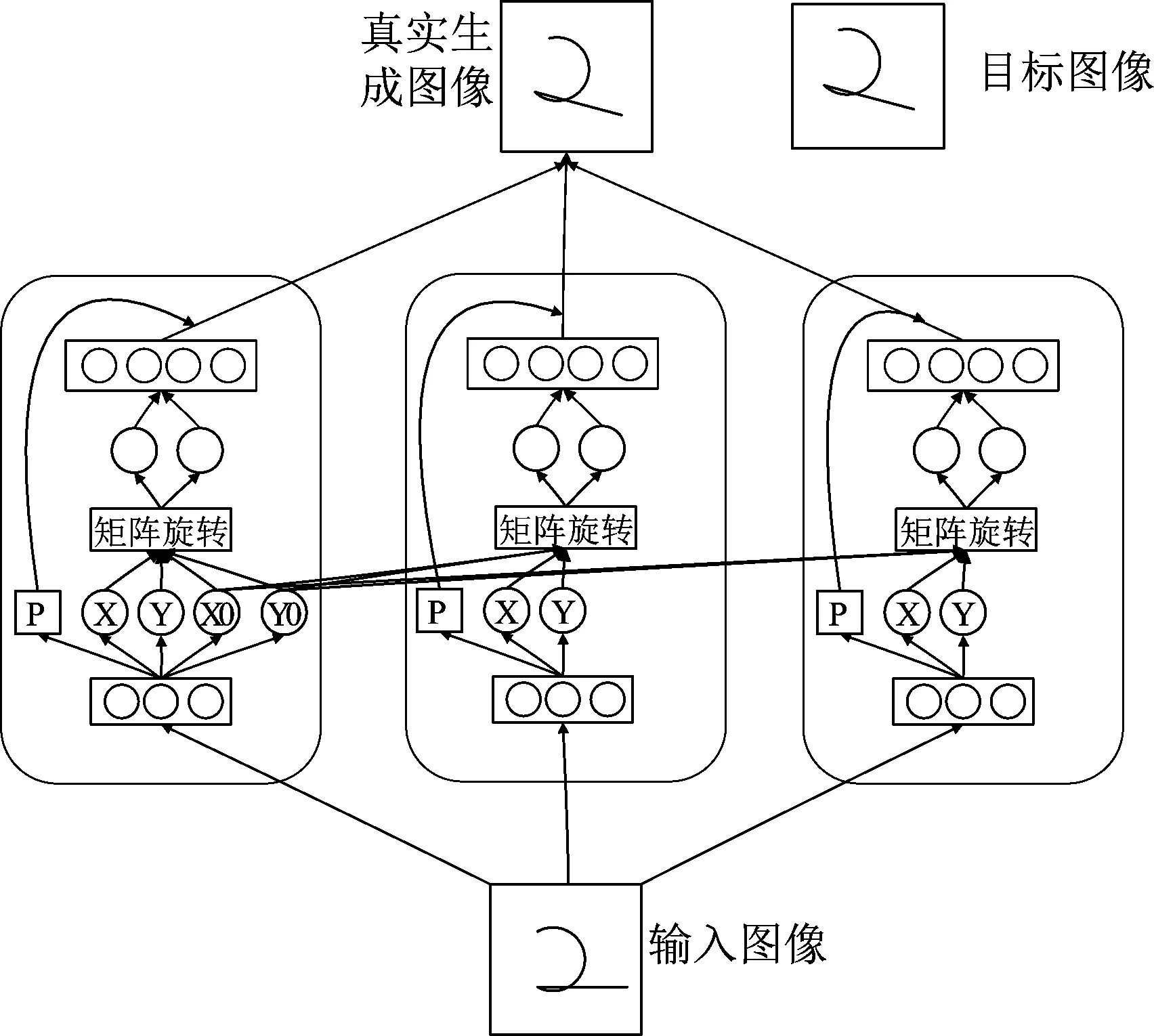
图3 固定中心点的旋转模型

2.3.2 固定旋转中心下的网络特征可视化的实现

固定中心点的胶囊网络的搭建仿照图3。识别单元层与生成单元层的输入输出尺寸与旋转变换下的网络保持一致。主要的训练参数如表3所示。

表3 胶囊网络主要训练参数

该网络的预处理过程与非中心固定点的胶囊网络的预处理过程相同，对输入输出图像的可视化处理以及位置坐标点的可视化处理也与非固定中心点的胶囊网络相同。在这里不做赘述。

2.4 卷积网络特征可视化

为进一步印证CNN空间信息表达的缺陷性，本文通过反卷积的可视化方法[10]，对分类训练的卷积网络的特征输出进行可视化。为增加对比性，CNN的输入数据为任意角度旋转之后的MNIST图像，具体网络的搭建如表4所示。

表4 卷积神经网络各层尺寸

3 胶囊以及卷积网络的特征可视化结果及分析

3.1 平移变换下的可视化结果及分析

最终得到的平移模型的可视化结果如表5所示。将逻辑识别层学到的位置坐标打印到表4中数字3的网络输入图像上，最后的结果如图4(a)所示，同时将平移之后的坐标，即逻辑生成单元的输入打印到表4中数字3的生成图像上，结果如图4(b)所示。

表5 平移胶囊网络可视化结果

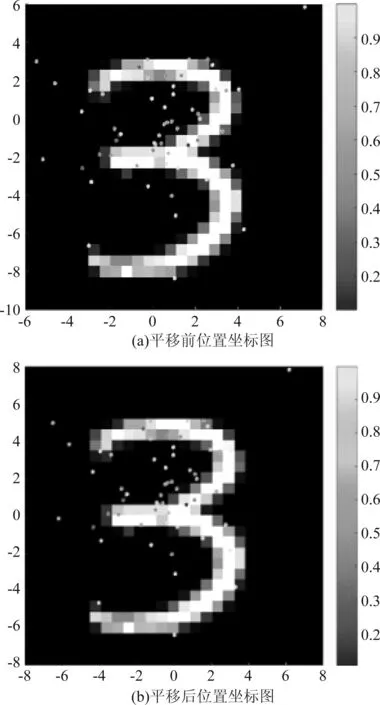
图4 网络平移坐标图

通过对表5中不同数字所对应的胶囊模块的输出特征图像的比较，可以发现不同的图片所对应的胶囊模块的姿态都是相似的，各模块的输出特征可以看成一个基图像，对最后的输出结果都有贡献，而最后得到的网络生成图像是概率值和输出特征图像的像素值加权和再做激活得到的结果。

与此同时，数字和数字之间的特征图像又会有灰度级上明暗的变化以及黑色边缘痕迹大小的改变。如表5中数字3对应的第43个胶囊模块的输出的特征并不明显，而该胶囊对应的概率值p只有0.10169839，说明在图片3中的对应的第43个胶囊视觉实体在输入图像中存在的概率很低。

3.2 旋转变换下的可视化结果及分析

对旋转胶囊网络的预处理前后网络输入图像、目标图像，激活前的图像以及训练得到的真实生成图像进行可视化，得到的结果如表6所示。对网络中的坐标信息进行可视化，得到的可视化结果如图5所示。(a)图初始位置坐标图中的坐标点也不再有规律的分布在输入图像上。而(b)图旋转后的位置坐标图则在目标图像上呈现出了比较好的结果。

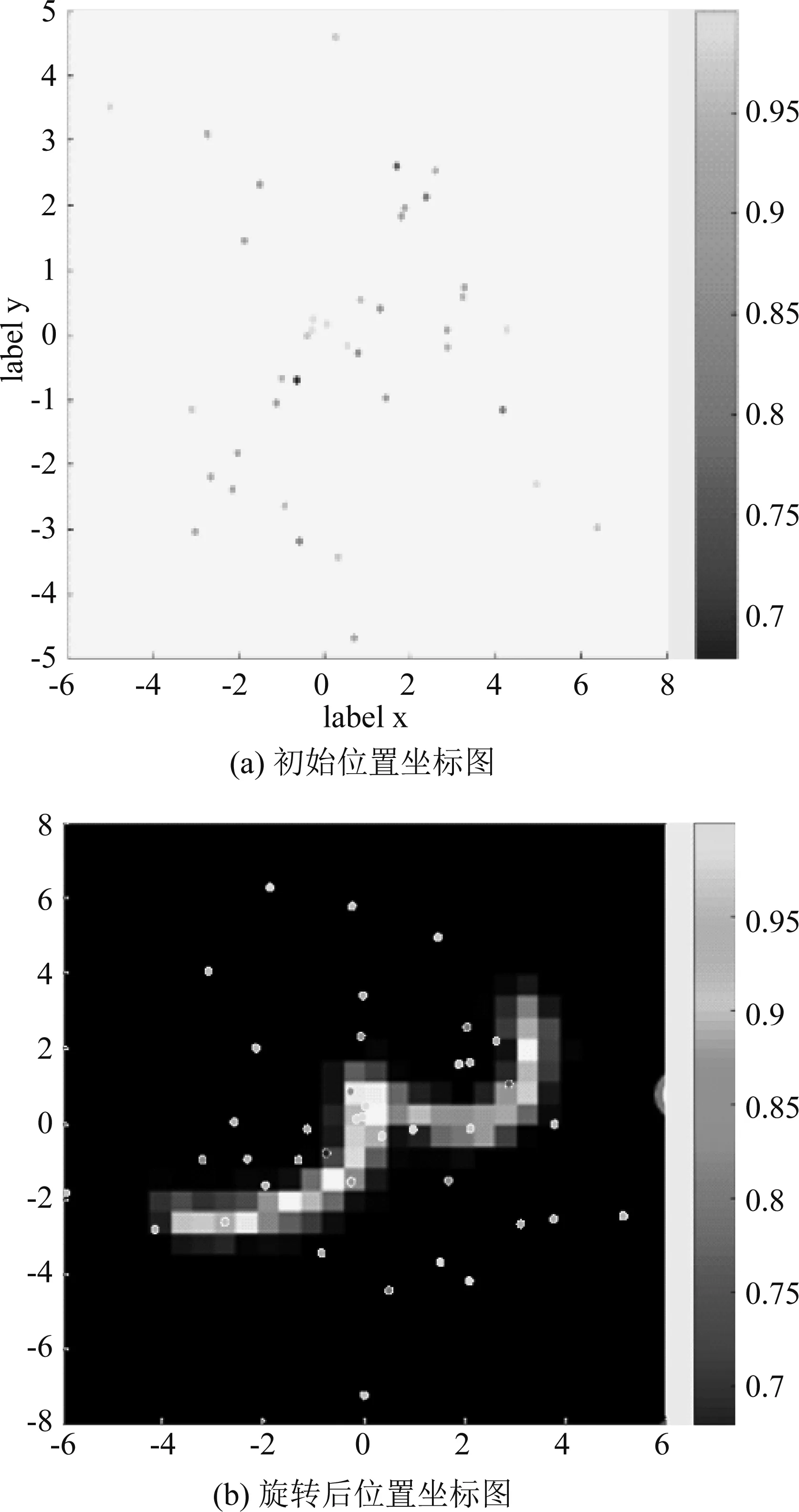
图5 网络旋转坐标图

最后得到的位置坐标中一部分有规律的分布在手写体数字上或边缘轮廓中，其他的坐标点分布在黑色背景上，最终得到的概率值的大小与坐标点是否在数字上没有关系，它们都对最后得到的真实生成图像有所贡献。通过两张坐标图彼此之间的联系，我们发现该旋转模型十分健壮，在学到的中心点不唯一的情况下，仍可以学到一系列合适的权重和偏差，使得最终的特征图像表现出良好的效果。

通过对表6中不同手写体数字对应的胶囊模块的输出特征图的比较中可以得出以下结论：

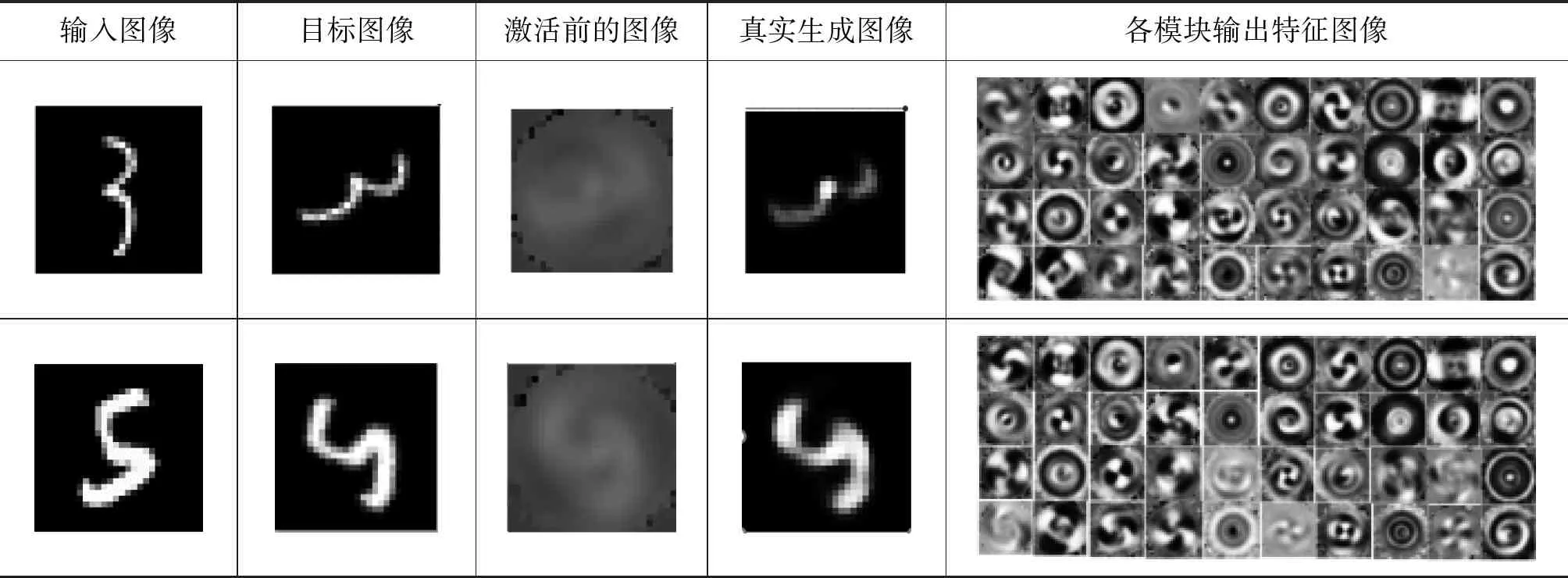
表6 旋转胶囊网络可视化结果

(1) 每个胶囊模块的输出可以大体分为两类：旋转类型、非旋转类型，如图6中(a)、(b)所示。

图6 特征类型

(2)真实图像由各胶囊模块的输出与概率p的加权和表示，不同图像所对应的胶囊姿态相似，不同的是亮度和旋转类型特征图像旋转角度的改变。

(3)结合旋转后的位置坐标以及相应的各胶囊输出模块的特征图像，发现在手写体数字轮廓上的点打印出来的特征图呈现非旋转类型，而没有在数字上的点所对应的特征图呈旋转类型。

3.3 固定旋转中心下的可视化结果及分析

同样，类似于论文中的非固定旋转中心的模型可视化，在可视化部分对固定旋转中心的胶囊网络做相同的处理。最终得到的结果如表7所示，由表7可知，训练得到的生成图像接近于目标图像。

通过对不同数字所对应的各个模块的输出特征图像的比较可知，固定旋转中心学习到的模块特征图像以及图像呈现出来的特点与非固定旋转中心学习到的特征图像并无本质区别。

最终训练得到的旋转中心坐标为：

(-1.46215999，1.41398716)

在此次实验结果之前，相同的训练参数，训练100次epoch得到的真实生成图像也是比较理想的，但是最终的旋转中心的位置与300次迭代的实验结果有很大的不同，这说明网络最后得到的旋转中心有很大概率是不同的，但对最后的训练效果并不会产生太大的影响。在整个训练模型中，所有的坐标都是通过学习得到的，所以相同数字图片的相同位置在不同的训练情况下得到的坐标点是不同的。

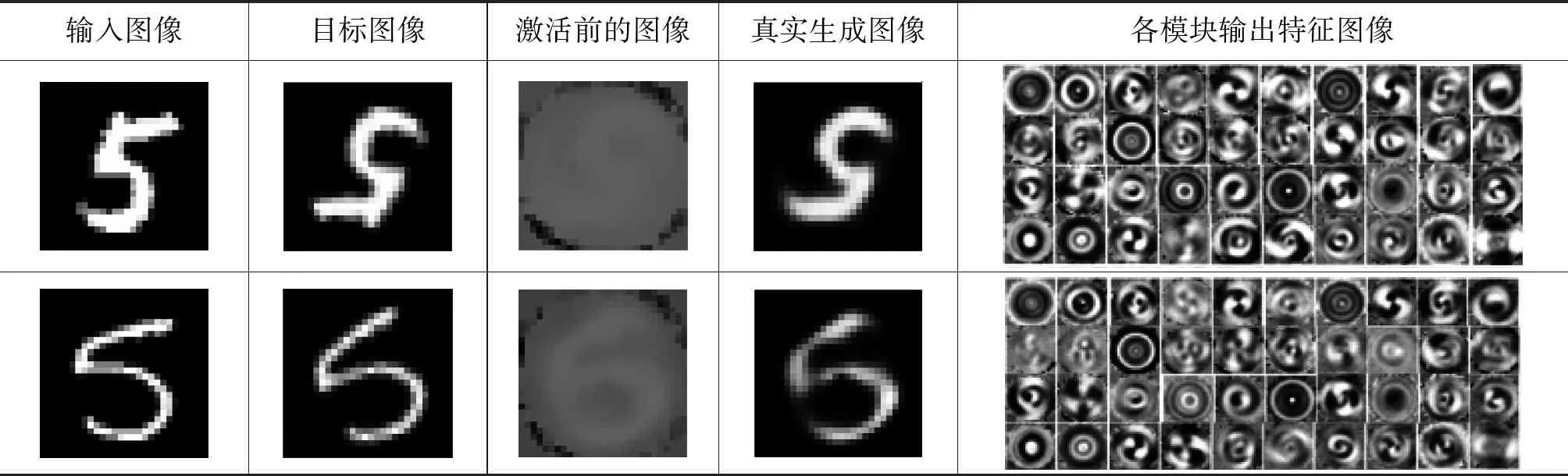
表7 固定中心点的旋转胶囊网络的可视化结果

对旋转之后的坐标点做可视化，得到的结果如图7所示。除图像的中心不再落在零点外，得到的结果与之前的网络结构的可视化结果相似，仍有大多数的位置坐标点分布在数字的边缘轮廓上。网络学到了数字边缘轮廓的位置信息。

3.4 卷积网络特征的可视化结果及分析

对于任意角度旋转下的卷积神经网络，在对处理后的MNIST数据集进行分类训练完成后，任意取一张图片卷积层的前五个神经元的特征输出进行可视化，得到的特征图像如表8所示。

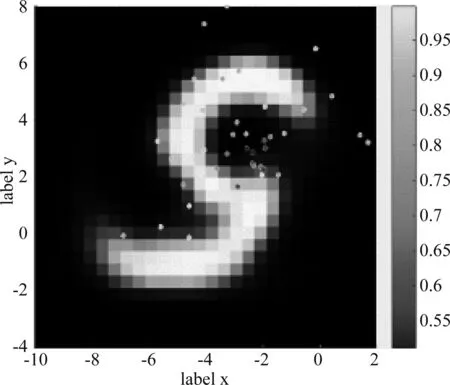
图7 旋转后坐标可视化

Conv1Conv2Conv3Conv4

表8中的特征图像针对的是数字3的像素矩阵，通过对表8中的特征图像的观察，我们发现各个神经元的输出特征图像几乎看不到空间位置的改变。基本上都是在原有数字3存在的位置上进行一些明暗或者细节特征信息的改变，当然在第一层卷积层提取到的特征信息是比较清晰的，也是一些比较简单的轮廓信息，随着卷积层的深入，特征信息的变化更加的复杂多样，细节信息更加丰富，但是空间信息的提取仍旧是比较有限的。

4 基于仿射变换的实验结果准确性的评价

为验证仿射变换下实验结果的准确性，评价真实生成图像与预处理后得到的目标图像的差距，本文用欧式距离损失函数值作为实验结果的评价指标。欧式距离损失函数的定义如式(2)所示：

(2)

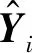
图8中的展示的是三种变换下600次epoch的损失函数图像，其中横坐标表示损失函数值的迭代次数，如图8(c)中横坐标表示损失函数迭代了300k次。在表5、表6、表7中，对比目标图像和生成图像，会发现两者或在像素强度上，或在边缘轨迹上会有不同，这是因为以上的训练结果最大的迭代次数只有300次，损失函数并未真正的收敛，但却已经获得比较好的训练结果。因为GPU资源有限，并尽可能的接近最后的收敛值，故我们选择了600次epoch的训练结果进行可视化输出。

我们最终发现600次epoch也并没有达到真正的收敛，但每个batch中的100张图片的总的欧式距离损失函数值总能降到10以下，最后得到的生成图像已经十分接近于目标图像。

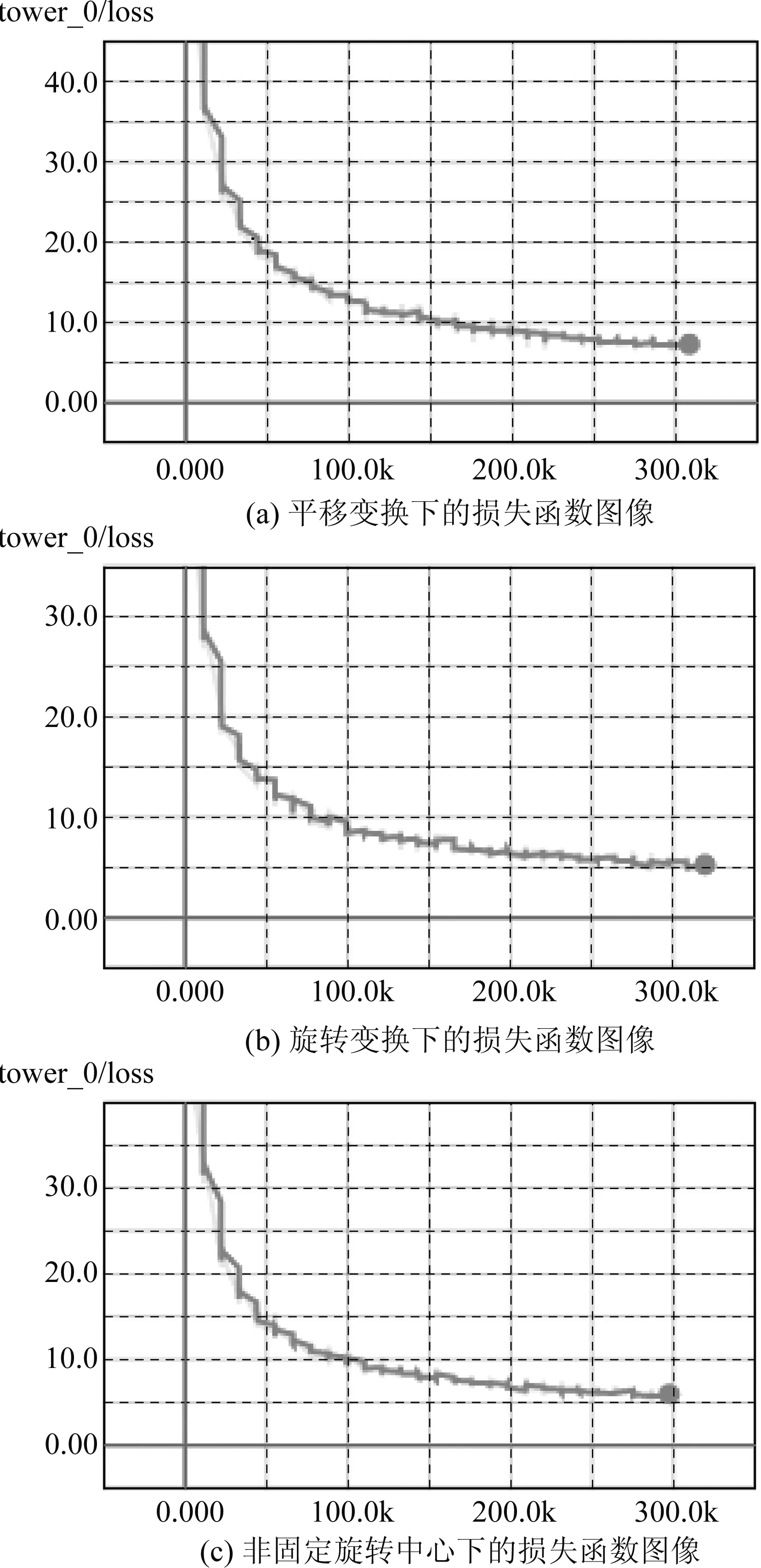
图8 仿射变换下的损失函数图像

5 结论

为了进一步加强对Capsule Network的实现过程以及其对位置信息的学习的理解，本文利用了Tesorboard等可视化工具对应用于平移、旋转的Capsule Network进行可视化，由实验结果可知，在胶囊网络内部，每个集成的胶囊模块都可以学到一种适用于大多数手写体数字的姿态，且每一个胶囊模块得到特征姿态都对最后的结果有所贡献。胶囊网络最后的确学到了手写体数字图像变换后的图像信息，但不同于卷积神经网络的是，胶囊网络在模型搭建时就考虑到了位置信息，最后逻辑生成单元得到的模块特征输出也是从位置信息转换而来的，所以Capsule Network对于位置信息的学习和处理是要明显优于传统的卷积神经网络的。