材料超高温动态拉伸SHTB实验方法的有效性分析*

李鹏辉,郭伟国,刘开业,王建军,谭学明

(西北工业大学航空学院，陕西 西安 710072)

同分离式Hopkinson压杆(SHPB)一样，分离式Hopkinson拉杆(SHTB)是测试材料在高应变率下拉伸力学性能的一种有效方法。但高温SHTB实验要求，既实现高应变率，又同时使试样处在高温、加载杆处在较低温度。由于拉伸加载时试样必须与加载杆连接，导致Hopkinson拉杆在高温下测试材料性能非常困难。

20世纪60 年代，Gilat等[1]将高温下Hopkinson杆实验方法分为两类：在线加热方式和预加热方式。在线加热是指，当试样和加载杆连接好后，直接对试样进行加热。由于试样与加载杆直接接触，加载杆温度不可避免地也会相应升高，进而在加载杆上造成温度梯度。佟景伟等[2]提出，当试样温度为500 ℃时，与室温的拉杆之间的温度梯度引起的应变和弹性模量相对误差分别为17.9%和13.3%，必须进行修正。夏开文等[3]利用传热学原理采用有限差分法对30CrMnSiA 在600 ℃下的实验结果进行了修正。过高的温度会造成材料微观组织的变化，温度修正方法可实现的温度不能超过加载杆的相变温度。为缩短热量传递时间，Rosenberg等[4]通过对感应线圈加载高频电流，可在1 min内将试样加热到700 ℃。但由于超大电流流过试样，可能对材料内部声子运动造成影响，而声子阻力是位错运动黏曳阻力的重要来源。另一种加热方式是预加热方式，Frantz等[5]首次建立一种弹性压杆运动机构，预先独立加热试样，利用机械装置推动加载杆与试样接触，接触时间可以控制在50～150 ms。

在目前高温SHTB实验方法中，基本都使用在线加热，允许的实验温度较低，加载杆端长时间在高温下撞击使用，会大幅度缩短寿命，影响实验测试的准确性。因此，本文中提出一种改进的高温SHTB实验方法，将试样与拉杆连接形式改进为钩挂连接，对狗骨状平板试样预先单独加热，利用两套气动同步装置推动试样与拉杆完成快速组装，实现准确的材料高温SHTB测试。针对这种高温SHTB实验技术中的几个关键问题，通过数值模拟、实验以及几种典型材料的高温动态拉伸性能测试相结合的方法进行深入讨论，以期获得一些重要结论。

1 高温SHTB实验系统

目前的SHTB中试样与加载杆的连接主要存在螺纹连接、胶粘连接和销钉连接等3种常用的连接形式，如图1(a)～(c)所示。可以看出，3种连接形式都属于固定连接，无法短时间内完成组装，并且连接形式的复杂性，如螺纹连接的间隙、螺纹尺寸、胶层厚度以及销钉预紧力等，容易造成应力波在连接处会产生较大的反射，引起测试误差。

针对常规拉伸试样连接方式无法离线加热的限制，我们提出一种狗骨状钩挂式平板试样，如图1(d)所示。试样被设计成两端带凸台的板状形式，加载杆端部为带挂钩的卡槽，通过加载杆卡槽与试样凸台的接触面传递拉伸载荷，连接方式简单，接触面紧密，为高温SHTB实验预加热试样后快速组装提供了基础。这个高温SHTB实验系统是在传统SHPB、SHTB实验系统[6-7]的基础上，通过加装高温炉和气动组装系统完成的，采用离线加热即试样与加载杆脱离进行加热，利用气动同步组装机构推动试样与加载杆快速组装[8]，同时完成加载，可以有效地避免加载杆温度过高对实验测试的影响，无须温度修正，实验数据准确。

图2为高温SHTB同步组装系统的示意图，主要由SHTB加载系统、高温炉、两个气动同步气缸、导轨和控制气路组成。两个加载杆端部加工出凹槽，尺寸与钩挂式试样尺寸配合。高温炉采用硅钼棒加热，加热温度可达1 600 ℃。导轨采用氧化铝陶瓷材料，避免加热过程中表面发生氧化与试样表面发生粘连，影响试样的推动。如图3所示，高温SHTB实验过程主要分为两步。

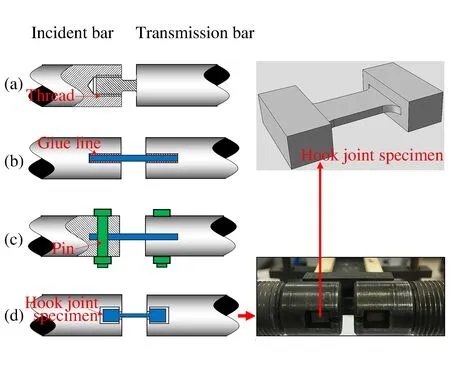
图1 SHTB试样连接形式Fig.1 Connection forms of SHTB specimen

图2 高温SHTB实验过程示意图Fig.2 Schematic diagram of SHTB experimental process at high temperature

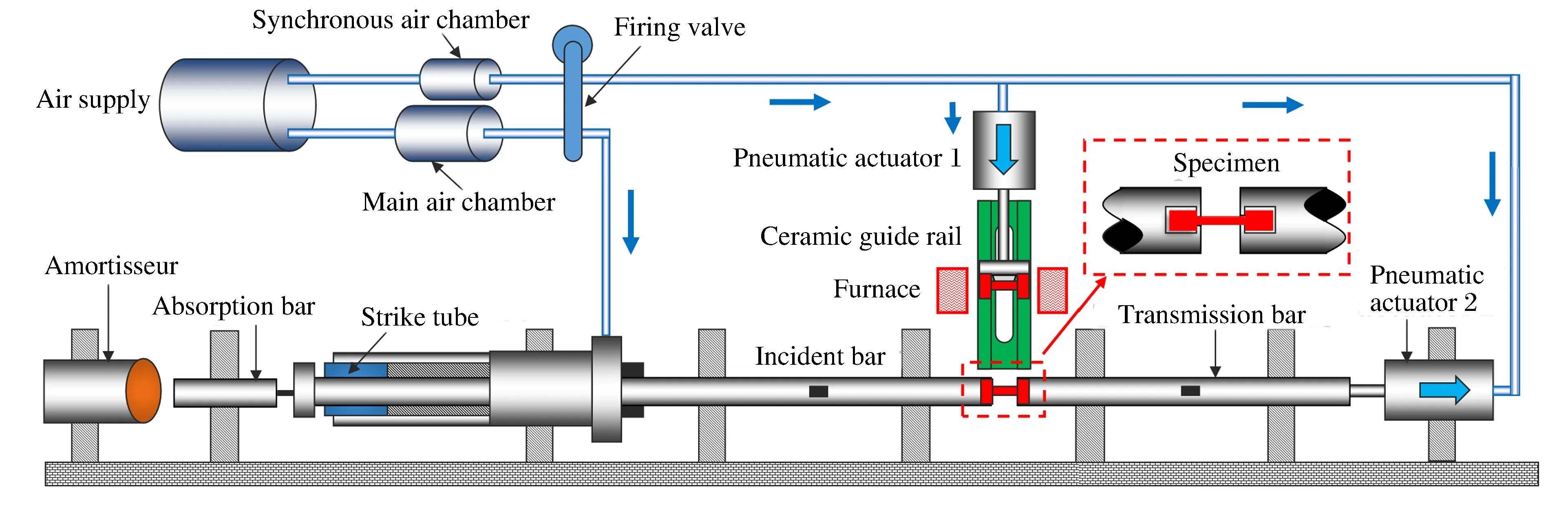
图3 高温SHTB实验装置示意图Fig.3 Illustration of setup for high temperature SHTB experiment

第1步：将试样置于位于加载杆侧面的陶瓷导轨之上，使它位于高温炉中央；调整入射杆和透射杆的位置，以确保组装过程中试样能顺利进入加载杆卡槽之内；通过加热装置将试样加热到预定温度。

第2步：打开双通道发射阀门，主气室内的压缩空气推动撞击杆撞击入射杆端部法兰盘，产生加载波；同步气室内的压缩空气一部分进入同步发射机构1推动试样沿导轨进入加载杆卡槽，一部分进入同步发射机构2向后拖动透射杆以消除试样与加载杆卡槽之间的配合间隙。之后，加载波传播至试样处完成加载。

2 高温SHTB实验技术中的关键技术问题

2.1 拉伸试样尺寸的优化

试样在动态拉伸变形过程中，需要处于一维应力状态并且沿轴向均匀变形，但由于试样端部的影响，其实际受力状态往往偏离这个状态。在静态实验中，通常尽量使试样标距段足够长以消除端部影响，但对于SHTB实验，标距段长度过长限制了更高应变率的实现。我们利用ABAQUS/Explicit有限元软件讨论钩挂式平板试样尺寸对实验测试的影响。

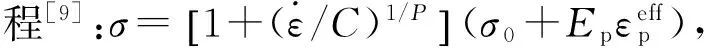
图4给出了不同应变率下利用钩挂式平板试样的数值模拟流动应力曲线与本构模型输入曲线的对比，可以看出在1 000和5 000 s-1下数值模拟结果与模型曲线均基本吻合，说明本文中采用的数值模拟方法是有效的。图5给出建议的有效试样尺寸设计及图纸，建议标距段长宽厚比例为8∶6∶1.2，该试样尺寸广泛适用于金属材料的动态拉伸测试。

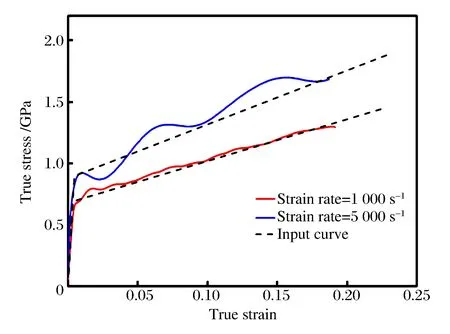
图4 数值模拟流动应力曲线与输入曲线对比Fig.4 Comparison of simulated flow stress curve with input curves

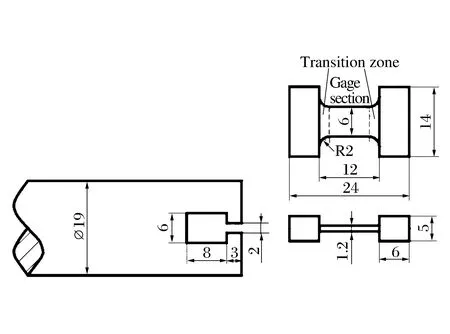
图5 钩挂式平板试样尺寸设计Fig.5 Size design of hook joint flat specimen

如图6(a)所示，固定试样宽度W=6 mm，试样厚度T=1.2 mm，选取不同试样长度L为4、6、8、10、12 mm，可以看出，不同试样长度对材料流动应力的影响在应变初期较小，在应变后期较明显。材料拉伸强度随试样长度的增加而升高。图6(b)给出了不同试样宽度对材料流动曲线的影响，可以看出材料标距段的宽度对材料测试的影响较明显。材料流动应力随着标距段宽度的增加而升高。选取不同试样标距段厚度，试样在不同真实应变(0.02、0.05、0.10)下的真实应力，如图6(c)所示。可以看出，在标距段厚度为1～1.6 m范围，材料流动应力随标距段厚度的变化波动较小，趋于平稳，说明在这个范围内应力分布较均匀。当标距段厚度取极端(0.1 m)时，材料流动应力偏差较大，实验数据不准确。当标距段厚度大于2 mm时，材料流动应力随厚度的增加逐渐降低。考虑到高温SHTB装置中组装机构的要求，选定试样标距段厚度为1.2 mm。考虑拉伸试样过渡段尺寸对实验测试准确性的影响，选定标距段长度为8 mm，宽度为6 mm，厚度为1.2 mm，选取不同的过渡段半径R分别为0、1、2、3和4 mm进行数值模拟，如图6(d)所示。可以看出，不同的过渡段尺寸对试样的屈服强度影响较小。随着应变的增大，过渡段尺寸对试样真实应力的影响增大。相同应变下的真实应力随着过渡段尺寸的增加而减小。陈滔等[10]提出，拉伸试样过渡段的变形会引起拉伸应变测量计算一定的失真。当试样过渡段与标距段比值小于0.25时，相对偏差约为5%，可忽略。本文中通过数值模拟和实验验证得出相似的结论，无过渡段时，在试样连接段和标距段根部出现较大的应力集中。当选取较小的过渡段尺寸(R=1 mm)时，过渡段变形量对试样应变测量的影响小于10%，与输入曲线的误差较小。

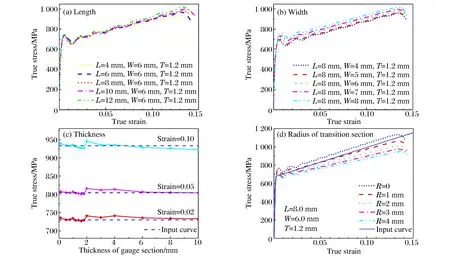
图6 试样尺寸对流动应力曲线的影响Fig.6 Effect of specimen size on flow stress curve

对于不同长宽比，试样在不同名义应变(0.10、0.15、0.20)下沿轴向的工程应变分布，如图7(a)所示。名义应变由加载杆上的反射应变求得。可以看出，对于不同长宽比，试样标距段根部应变比中间部位小。随着长宽比的增加，标距段中间部位应变分布均匀的区域增大。图7(b)为试样轴向应力沿宽度方向的分布情况。随着长宽比增大，试样沿宽度方向应力分布均匀性增加，试样变形更接近一维应力状态。采用公式η=σmax-σmin，表征试样偏离一维应力状态的程度，当L/W=8/6和L/W=10/6时，沿宽度方向应力偏离程度小于3%，当L/W=6/6时，试样偏离一维应力的程度超过6%。当试样长宽比L/W≥8/6时，试样达到较好的轴向应变均匀性，且试样变形接近一维应力状态。考虑试样过长将限制SHTB实验所能实现的最大应变率，建议长宽比为8∶6。

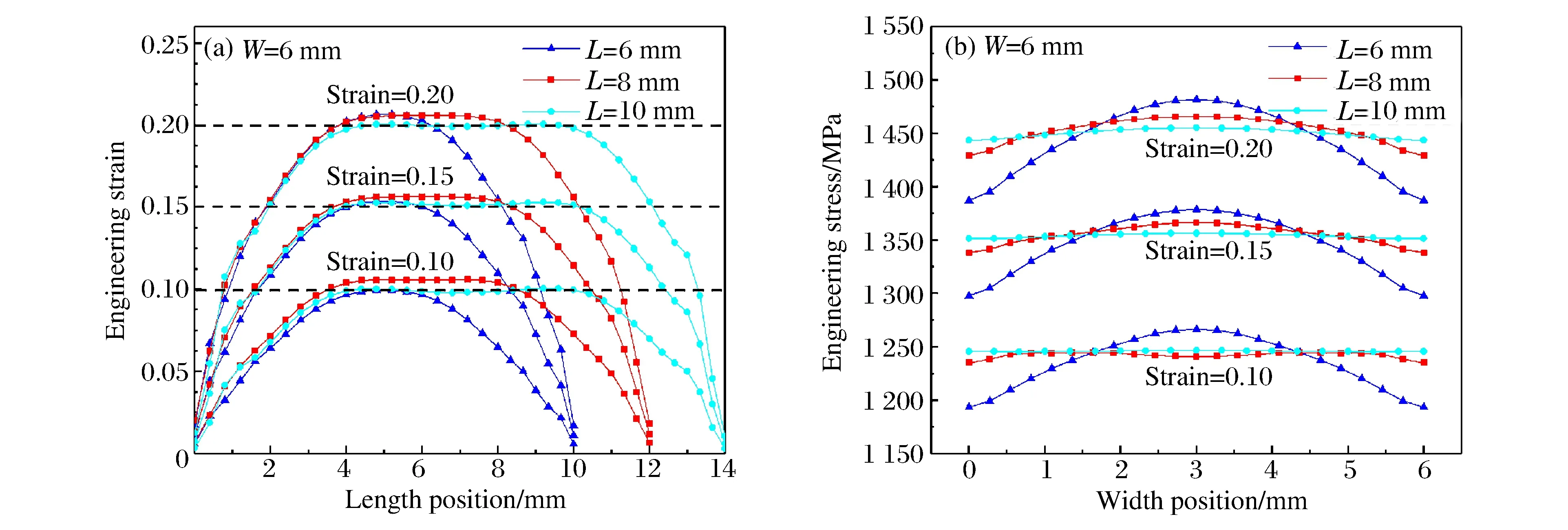
图7 钩挂式板状试样不同长宽比下应力和应变分布Fig.7 Flat hook-joint specimen’s stress and strain distribution at different ratios of length to width

为验证钩挂式平板试样的有效性，分别通过数值模拟和实验对钩挂式试样的准确性进行验证。数值模拟和实验中钩挂式平板试样均为长度8 mm、宽度6 mm、厚度1.2 mm，螺纹连接试样标距段直径为5 mm、长度为5 mm。数据处理方法选取为Hopkinson拉伸实验中经典“一波法”理论。图8(a)为钩挂连接与螺纹连接数值模拟结果与本构模型输入曲线的对比，三者基本重合, 可以说明本文中所采用的数值模拟方法以及参数设定合理，模拟结果有效。图8(b)为钩挂连接和螺纹连接两种形式的45钢在1 000 s-1、室温下的SHTB实验曲线对比，每种试样形式重复实验3次。结果表明，钩挂连接形式的流动应力曲线与螺纹连接基本一致。相比螺纹连接流动曲线在应变初期出现的剧烈抖动，钩挂连接流动应力曲线的抖动较小，能更真实地表征材料的塑性流动行为。

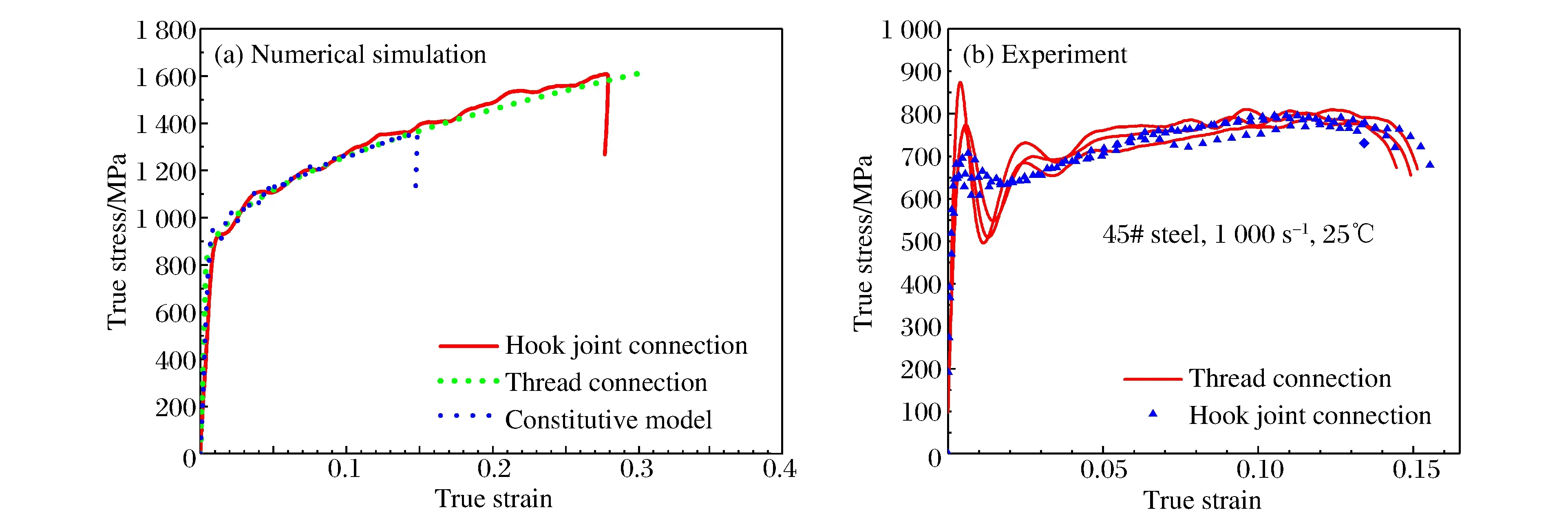
图8 钩挂连接与螺纹连接数值模拟和实验结果对比Fig.8 Comparison of numerical simulation and experimental results between hook joint and thread connection

2.2 加载杆温度梯度的实验误差分析

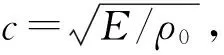
图9 钛合金TC4弹性模量随温度变化Fig.9 Elastic modulus of titanium alloy TC4 versus temperature

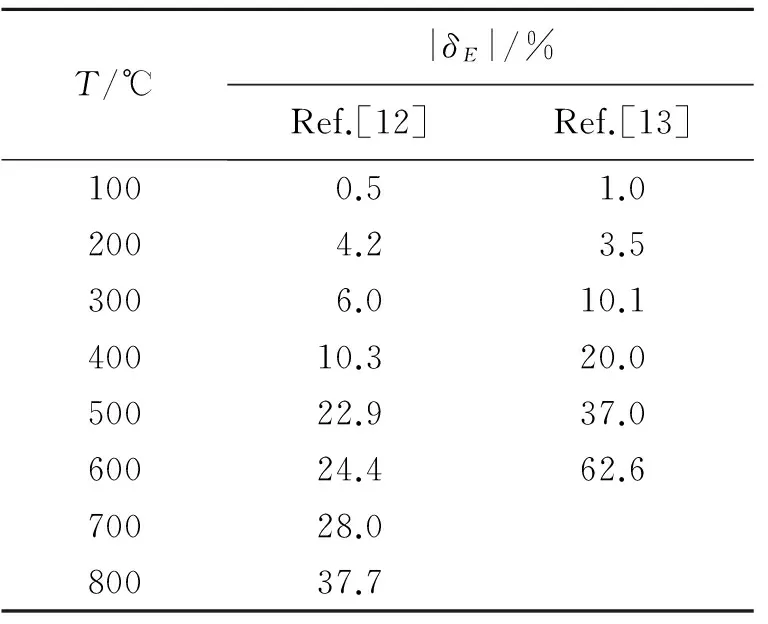
T/℃|δE|/%Ref.[12]Ref.[13]1000.51.02004.23.53006.010.140010.320.050022.937.060024.462.670028.080037.7

2.3 冷接触时间分析

试样与加载杆完成组装和应力波对试样开始加载之间的时间间隔称为冷接触时间(cold contact time，CCT)。对于本高温SHTB实验方法，存在两次冷接触过程。第1次为试样加热至预定温度后在温度较低的导轨上滑动的过程；第2次为试样从进入加载杆卡槽到加载波开始加载，高温试样与卡槽接触的过程。

整个实验过程中各个过程的时间，如图10所示。t1、t2、t3分别为阀门打开后气室内的气体沿气路进入发射炮管、同步气缸1和同步气缸2的时间。t4为撞击管由初始位置到与加载杆法兰盘撞击所用时间，t4=2L/v；t5为入射波沿入射杆传播到试样处所用时间，t5=L1/c0；t6为同步气缸1开始运动到推动试样进入加载杆卡槽所用时间，t7为同步气缸2开始运动到试样与加载杆卡槽间隙消除所用时间。t3+t7>t2+t6，是保证同步组装能够完成的条件；t1+t4+t5>t3+t7，是保证入射波对试样加载前、组装已完成的条件。

如图11所示，采用激光传感器直接测量两次冷接触时间。信号1为试样开始沿导轨从高温炉中出来的时刻；信号2为试样到达加载杆卡槽内的时刻；信号3为同步气缸2拖动透射杆，使试样与加载杆卡槽间隙消除的时刻；信号4为加载波开始对试样加载的时刻。信号2与信号1的时间间隔即为第1次冷接触时间，其值为44 ms；信号4与信号2的时间间隔为第2次冷接触时间，其值为83 ms。整个过程从组装开始到对试样加载，其时间为127 ms。冷接触时间的实验测定过程中，同步气压和发射气压均保守地选取满足同步组装顺利完成条件下的较小气压，因此测得的冷接触时间是保证同步组装顺利完成的最大可能值，为127 ms。真实实验中的冷接触时间均不大于该最大可能的冷接触时间，真实实验中试样温度的下降值以及加载杆杆端的温升值均小于本文中给出的结果。

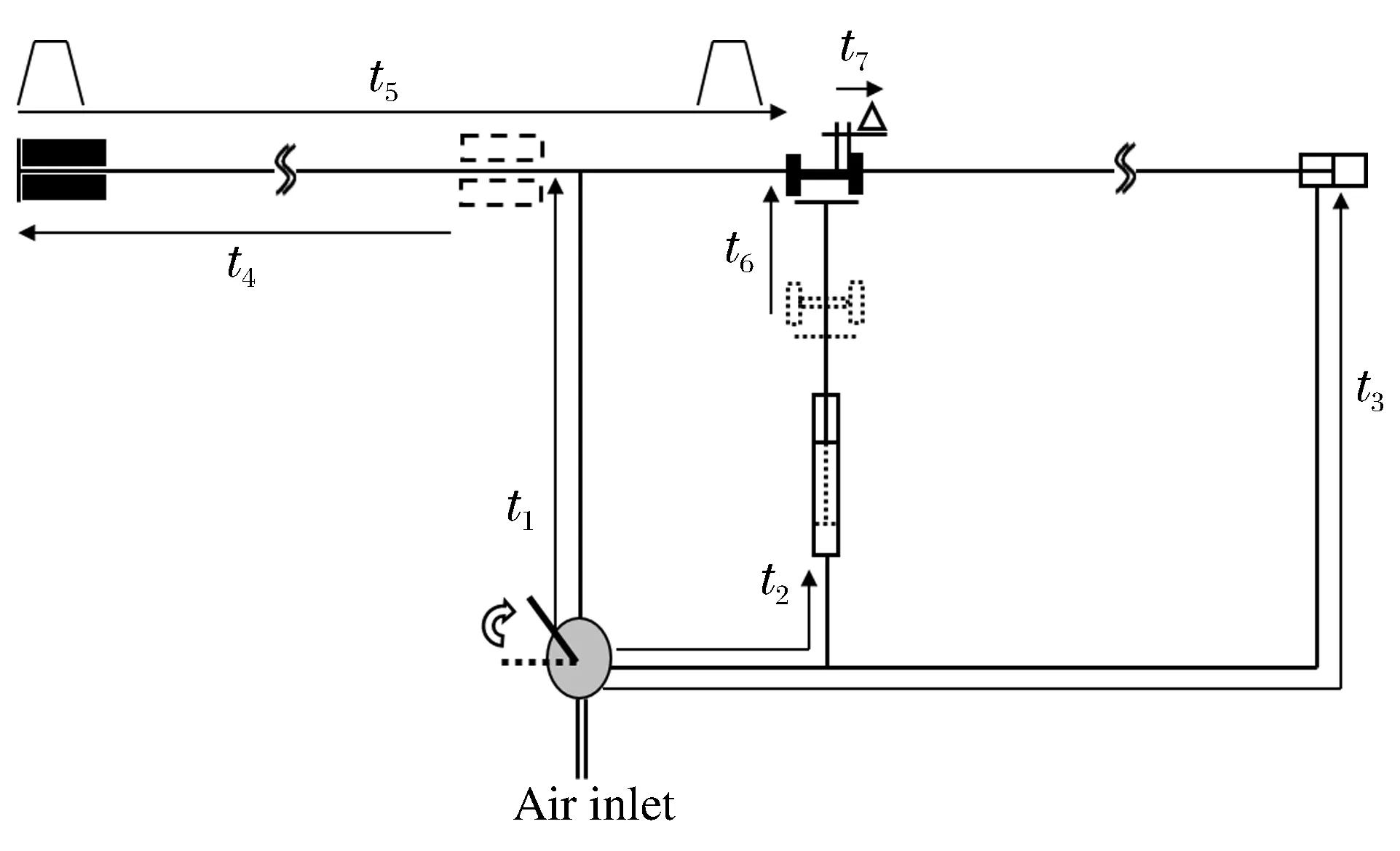
图10 冷接触时间示意图Fig.10 Cold contact time

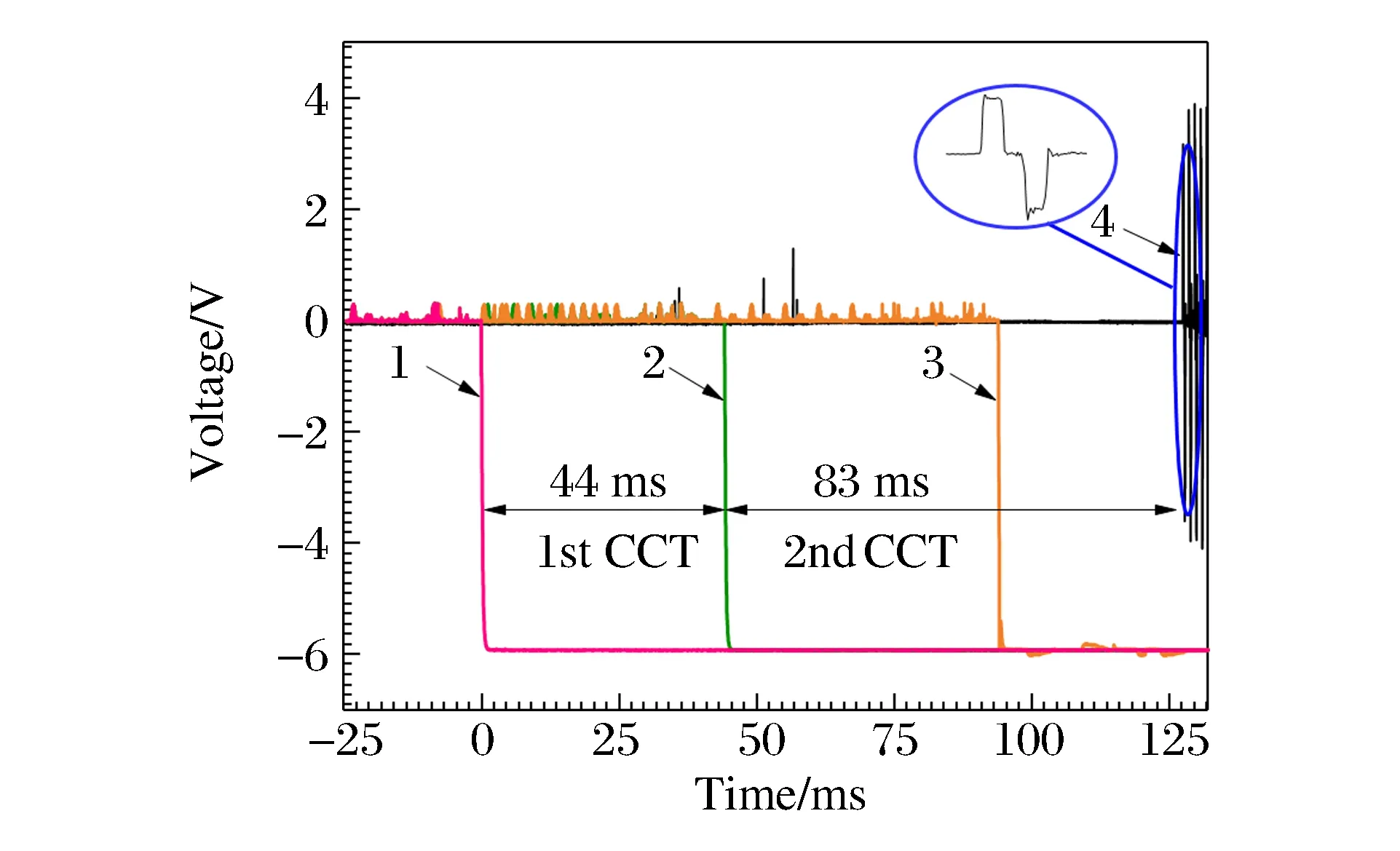
图11 冷接触时间测试Fig.11 Cold contact time measurement

2.4 冷接触过程温度变化分析

在冷接触过程中，由于高温试样与常温环境以及加载杆之间存在巨大的温度梯度，会发生剧烈的热交换，从而引起试件上的温度下降和加载杆局部的温度上升，是导致高温SHTB实验误差的主要原因。通常，热交换包括3种形式，即热辐射、热对流和热传导。利用ABAQUS软件研究整个冷接触时间内试样和加载杆端温度的变化，试样初始加热温度设为1 400 ℃，环境温度设为20 ℃，单元采用八节点线性热传导单元(DC3D8)，计算时间为500 ms。

辐射换热分析。对于真实物体，其热辐射都小于同等温度下的黑体辐射(Φ=AσT4)，热辐射量由斯忒藩-波尔兹曼定律的修正公式Φ=εAσT4确定，ε为表面发射率。基于保守考虑，将试样视为黑体，即取物体表面发射率ε=1。图12(a)～(b)为50、130、200、500 ms时刻试样沿宽度方向和厚度方向的温度分布图。由于热辐射是由试样表面进行，因此：沿宽度方向，边缘温度低于中部温度；沿厚度方向，表面温度与中部温度基本相同。

对流换热分析。第1次冷接触过程中，试样在导轨上滑动，属于强制对流换热；而第2次冷接触过程中，试样静止地处于加载杆卡槽内，属于自然对流换热。强制对流的表面换热系数比自然对流大一个数量级。因此，第2次冷接触过程中对流换热对试样温度的影响将不予考虑。试样的表面对流换热系数h=0.066 4(λ/l)(Rex)1/2(Pr)1/3，式中Rex是以x为特征长度的雷诺数，Pr=v/a为普朗特数。对流换热过程中，试样沿宽度方向和厚度方向的温度分布如图12(c)～(d)所示。可以看出，其温度分布规律与热辐射传热相同，但温度下降速度较热辐射低。

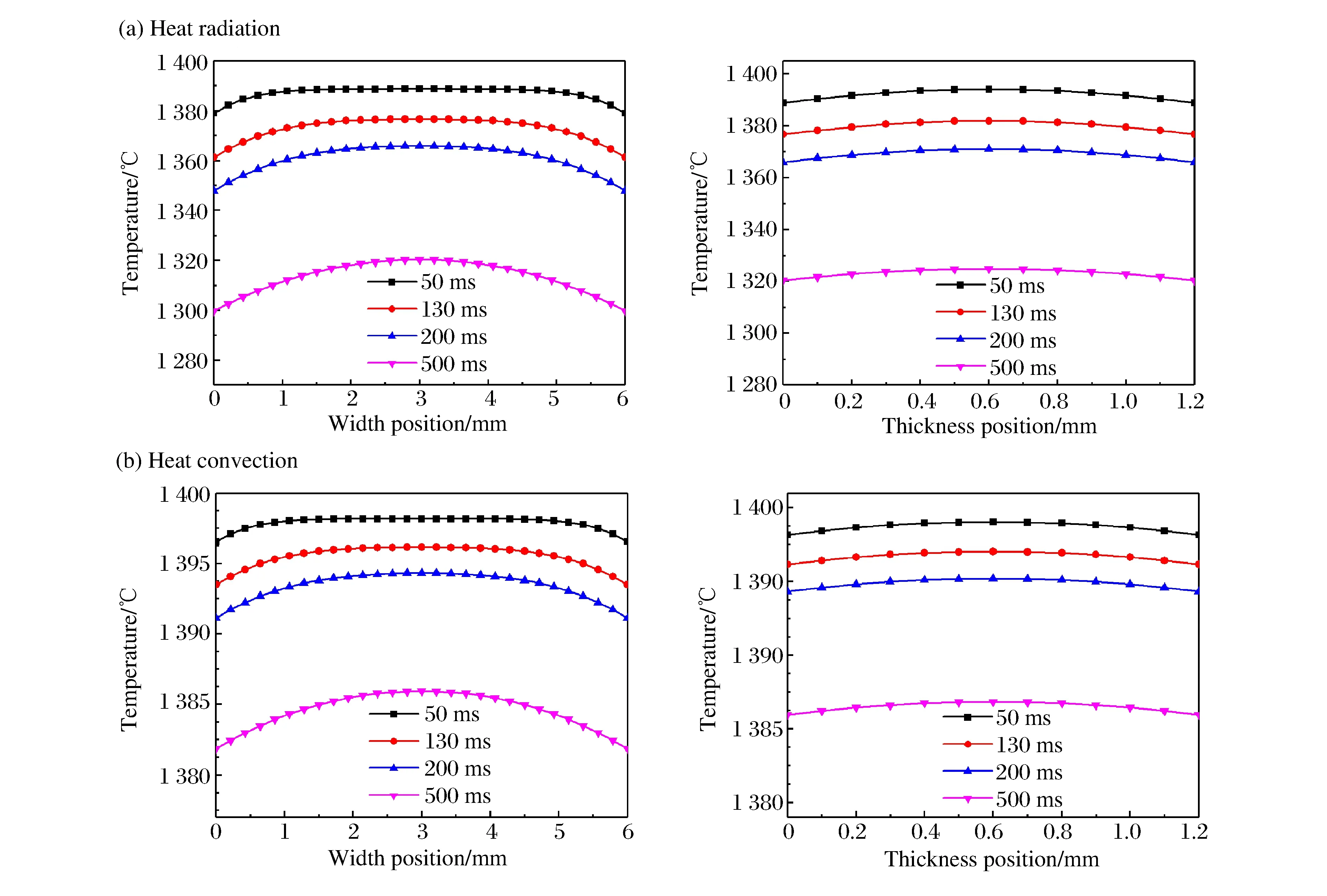
图12 热辐射和热对流过程沿宽度和厚度方向温度分布Fig.12 Temperature distribution along width and thickness

接触传热分析。第1次冷接触为试样在导轨上滑动的热传导过程，第2次冷接触为试样与加载杆接触的热传导过程，接触换热系数取为3 200 W·m-2·℃-1。由于陶瓷导轨中间部分处于高温炉内，导轨温度高于环境室温，本文中保守地设置导轨初始温度为室温20 ℃，因此真实状态中试样在冷接触过程中的温度下降值应小于数值模拟值。

图13分别为两次冷接触过程中沿试样中线轴向方向在不同接触时间下的温度分布以及试样在500 ms时的整体温度分布云图。由于两次冷接触过程中，直接与导轨和加载杆卡槽接触的是试样的凸台部位，因此，冷接触带来的温度下降集中发生在试样钩挂凸台部分和过渡段，标距段温度并未出现明显下降。

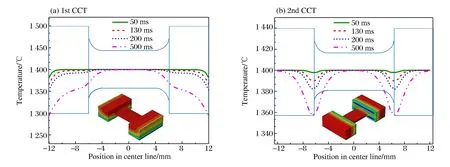
图13 冷接触过程试样中线温度分布Fig.13 Temperature distribution along center line of specimen during cold contact

热辐射、热对流和两次冷接触热传导对试样标据段平均温度的影响，如图14所示。可以看出，热辐射对试样温度影响最大，热对流次之。而热传导过程中，由于与导轨和加载杆直接接触的是试样的凸台段，而非标距段，因此，它对试样标据段平均温度的影响远小于热辐射和热对流。第1次冷接触(t=44 ms)存在热辐射传热、热对流传热和第1次接触传热，第2次冷接触(t=83 ms)存在热辐射传热和第2次接触传热，试样标距段平均温度下降幅值近似为第1、2次冷接触5项传热温度下降幅值之和。

为评估实验标距段在整个冷接触过程中的温度变化程度，选取数值模拟结果中试样标距段的全部单元，计算全部单元在整个冷接触过程中温度变化值的平均值、最大值以及最小值，他们随试样初始温度变化的曲线如图15所示。试样标距段的最大的温度下降出现在标距段外表面的边角处，最低的温度下降出现在试样中心部位。当试样初始加热温度为1 000、1 200、1 400、1 600、1 800 ℃时，试样标距段平均温度下降值分别为8.38、16.67、22.91、36.27、53.31 ℃，温度降低幅度分别为0.84%、1.39%、1.64%、2.27%、2.96%。

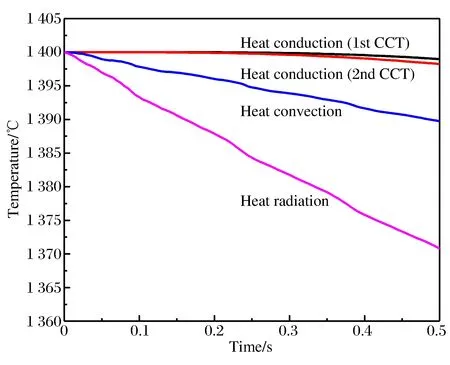
图14 热辐射、热对流和热传导对标距段平均温度的影响Fig.14 Effect of heat radiation, heat convection and heat conduction on average temperature

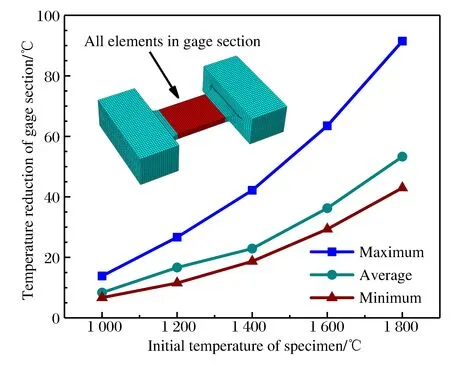
图15 标距段温度下降随试样初始温度变化Fig.15 Average temperature of gage section drop versus specimen initial temperature

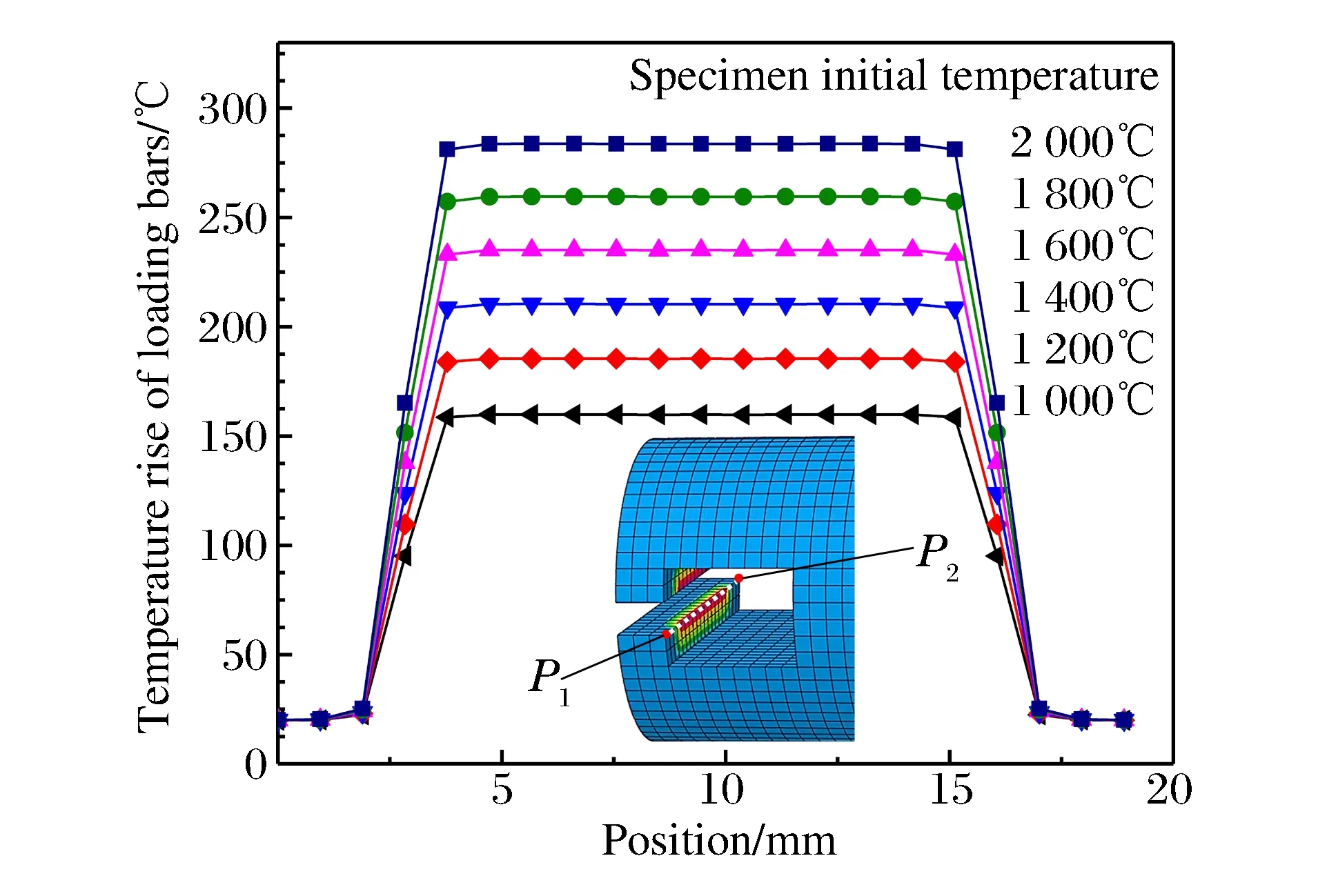
图16 不同加热温度引起的加载杆端温升Fig.16 Temperature rise of loading bars caused by different heating temperatures

第2次冷接触过程中，试样与加载杆的组装过程将引起加载杆端温度的上升。加载杆端温度分布如图16所示，加载杆端的卡槽边缘与试样凸台根部接触的部分温度变化明显，其他位置温度基本保持不变。设定试样加热至初始温度1 000～2 000 ℃，第2次冷接触过程中，加载杆端温升最大处(如图16中虚线P1-P2所示)的温度变化曲线如图16所示。可以看出，利用本文中高温SHTB拉伸实验方法，当试样加热至1 200 ℃时，冷接触过程引起的加载杆端局部最大温升约为180 ℃，不会引起加载杆的弹性模量等材料力学属性的变化，可以有效地避免加载杆温度梯度对测试的影响。

由计算结果可以看出：当实验温度为1 200 ℃时，试样平均温度仅下降约1.3%，加载杆端温升仅为180 ℃；当实验温度为1 400 ℃时，试样平均温度下降约1.7%，加载杆端温升约为210 ℃。因此，与传统高温SHTB实验方法不同，本文中提出的高温SHTB实验装置和实验方法有效地避免了加载杆在加热过程中的温度梯度对实验测试准确性的影响，同时由同步组装过程中冷接触引起的试样温降也较小，对实验结果的精确性基本没有影响。

3 高温SHTB实验装置的实验验证

基于建立的新型超高温SHTB实验技术，对3D打印钛合金TC4材料和镍基单晶高温合金DD6在103量级应变率、温度25～1 200 ℃范围的拉伸力学行为进行研究，同时进一步验证本文中提出的高温SHTB实验装置和方法的高效性和准确性。

3D打印TC4在1 000 s-1下的拉伸流动应力表现出明显的温度敏感性[14]。如图17(a)所示，随着温度的升高，材料的流动应力呈下降趋势。材料在应变初期的流动曲线出现一段明显下降，这是由于高应变率引起的材料内部绝热温升导致的温度软化效应。之后，随着应变硬化的增强，进入应变硬化与温度软化相互平衡的过程，材料的流动应力曲线变得相对平缓。如图17(b)所示，镍基单晶高温合金DD6在3 000 s-1、实验温度25～1 200 ℃时，材料的流动应力随温度的升高而升高，在某个温度下，流动应力达到了峰值。该峰值温度约为1 000 ℃，超过该温度，材料出现明显的应变软化，并且流动应力随着温度升高而降低[15]。

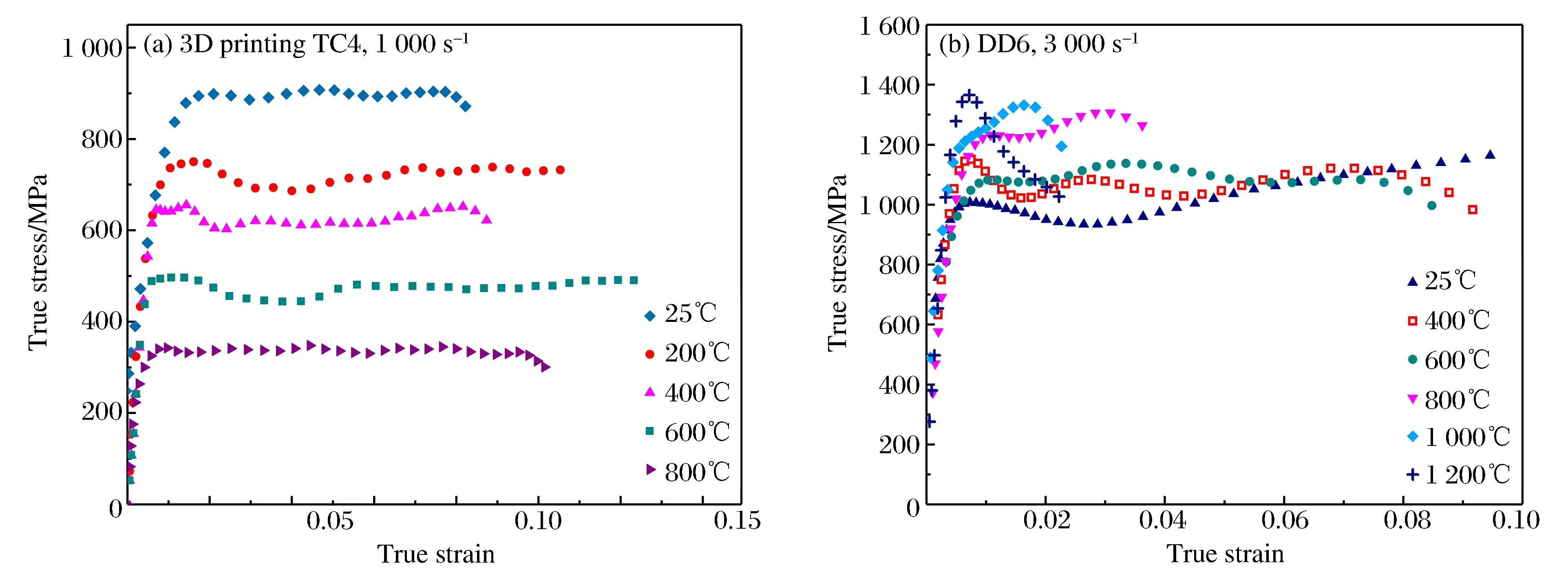
图17 典型材料的动态拉伸真实应力-应变曲线Fig.17 Dynamic true tress versus true strain

4 结 论

建立了一种新型超高温分离式Hopkinson拉杆实验装置和方法，将传统螺纹拉伸试样改进为狗骨状钩挂式平板试样，采用离线加热、快速钩挂连接同步组装的方式，可精确测试材料在高温(约1 200 ℃)、高应变率(约103s-1)耦合作用下的动态拉伸力学性能，并针对该实验技术中的几个关键问题进行了研究。

(1)钩挂式平板拉伸试样的动态流动应力曲线与螺纹拉伸试样的一致，且流动应力曲线在初始段的抖动相比螺纹试样的较小，能更真实地表征材料的塑性流动行为。

(2)钩挂式平板试样的几何尺寸影响材料流动应力曲线的测试。基于数值模拟和实验结果，给出建议的标距段几何尺寸比例为长∶宽∶厚=8∶6∶1.2，可以有效测定材料的高温动态拉伸性能。

(3)通过精确控制气压可实现有效的快速同步组装。实验测定整个冷接触时间为127 ms; 当实验温度为1 200 ℃时，在整个冷接触时间内试样平均温度仅下降约1.3%，而加载杆端温升仅为180 ℃，有效地避免了温度梯度分布对实验测试准确性的影响。

(4)利用建立的高温SHTB实验方法研究了3D打印TC4、镍基单晶高温合金DD6的高温动态拉伸力学行为，同时充分验证了该高温SHTB实验装置和方法的有效性和准确性。在高应变率拉伸载荷下，3D打印TC4表现出明显的温度软化效应，而DD6在1 000 ℃左右出现明显的反常应力峰值。

[1] GILAT A, WU X. Elevated temperature testing with the torsional split Hopkinson bar[J]. Experimental Mechanics, 1994,34(2):166-170.

[2] 佟景伟,高丛峰,李鸿琦,等.温度梯度对拉伸SHB试验误差的数值分析[J].爆炸与冲击,2001,21(4):277-281.

TONG Jingwei, GAO Congfeng, LI Hongqi, et al. Numerical analysis on the error in the split Hopkinson tension bar test at temperature gradient[J]. Explosion and Shock Waves, 2001,21(4):277-281.

[3] 夏开文,刘文彦,唐志平.30CrMnSiA钢高温动态力学性质的实验研究[J].爆炸与冲击,1998,18(4):310-316.

XIA Kaiwen, LIU Wenyan, TANG Zhiping. Experimental study of dynamic properties of 30CrMnSiA steel at high temperature[J]. Explosion and Shock Waves, 1998,18(4):310-316.

[4] ROSENBERG Z, DAWICKE D, STEADER E, et al. A new technique for heating specimens in split-Hopkinson-bar experiments using induction-coil heaters[J]. Experimental Mechanics, 1986,26(3):275-278.

[5] FRANTZ C E, FOLLANSBEE P S, WRIGHT W J. New experimental techniques with the split Hopkinson pressure bar[C]∥8th International Conference on High Energy Rate Fabrication. 1984.

[6] GUO W G, NEMAT-NASSER S. Flow stress of nitronic-50 stainless steel over a wide range of strain rates and temperatures[J]. Mechanics of Materials, 2006,38(11):1090-1103.

[7] 郭伟国.高导无氧铜在大变形、不同温度和不同应变率下的流动应力和本构模型[J].爆炸与冲击,2005,25(3):244-250.

GUO Weiguo. Flow stress and constitutive model of OFHC Cu for large deformation, different temperatures and different strain rates[J]. Explosion and Shock Waves, 2005,25(3):244-250.

[8] 郭伟国,朱泽,曾志银,等.高温高应变率拉伸同步实验装置:ZL 2012 2 0438121.0[P].2013-04-17.

[9] LI Yulong, ZHANG Yongkang, XUE Pu. Study of similarity law for bird impact on structure[J]. Chinese Journal of Aeronautics, 2008,21(6):512-517.

[10] 陈滔,李庆斌,管俊峰,等.霍普金森拉杆装置螺纹过渡段变形测量修正[J].工程力学,2013,30(7):276-281.

CHEN Tao, LI Qingbin, GUAN Junfeng, et al. Deformation measurement correction for the threaded connection and transition part utilizing SHTB[J]. Engineering Mechanics, 2013,30(7):276-281.

[11] KLEPACZKO J R, RUSINEK A, RODRGUEZ-MARTNEZ J A, et al. Modelling of thermo-viscoplastic behaviour of DH-36 and Weldox 460-E structural steels at wide ranges of strain rates and temperatures, comparison of constitutive relations for impact problems[J]. Mechanics of Materials, 2009,41(5):599-621.

[12] 张树华.TC4、16Mn合金及Al2O3陶瓷的高温弹性模量[J].高压物理学报,1995,9(2):133-138.

ZHANG Shuhua. High temperature elastic moduli of TC4, 16Mn and Al2O3ceramics[J]. Chinese Journal of High Pressure Physics, 1995,9(2):133-138.

[13] JASTRZEBSKI Z D, KOMANDURI R. The nature and properties of engineering materials[M]. Wiley, 1975.

[14] LI P H, GUO W G, HUANG W D, et al. Thermomechanical response of 3D laser-deposited Ti-6Al-4V alloy over a wide range of strain rates and temperatures[J]. Materials Science and Engineering: A, 2015,647:34-42.

[15] WANG J, GUO W G, LI P, et al. Dynamic tensile properties of a single crystal nickel-base superalloy at high temperatures measured with an improved SHTB technique[J]. Materials Science and Engineering: A, 2016,670:1-8.