高冲击下引信用固态钽电容的参数变化

李长龙，高世桥，牛少华，刘海鹏

(北京理工大学机电学院，北京 100081)

智能引信通常用于判断战斗部最佳起爆位置、最优起爆时机以及确保能够安全引爆战斗部，而钽电容在智能引信中起着贮能、点火、解耦、延时等作用。因此，钽电容的质量对智能引信的起爆控制系统起着决定性的作用。当炮弹发射时，会产生突发性高机械冲击载荷，钽电容经受高冲击载荷作用时会发生特性变化。钽电容在高冲击载荷下的参数变化特性是决定智能引信实现其功能的关键因素之一。

针对钽电容在环境载荷下的参数变化特性已做了许多研究。徐建军研究了钽电容在高温下的漏电流变化现象[1],Alexander研究了钽电容在机械振动、反偏电压作用下的电参数变化特性[2-3],程融发现钽电容在冲击应力下易出现瞬时短路的现象[4],何荣华等对高过载下军用电容的失效进行了探讨，并分析了电容失效对引信的影响[5]。

虽然关于钽电容的参数变化问题已做了大量研究，但有关参数变化的影响因素主要集中在振动、温度等环境载荷方面，而针对冲击载荷对钽电容影响的研究比较少。即使有关于钽电容经受冲击载荷作用的研究也主要集中在实验现象上，而缺少对引起参数变化的内部机理的分析。本研究首先通过实验手段分析了钽电容在冲击载荷作用下电容量、漏电流的变化特性，然后对电参数变化特性分析其内在机理。

1 实验设计

1.1 钽电容结构

固态钽电容主要包括阳极Ta、电介质Ta2O5、阴极MnO2。阳极Ta是由钽粉压制烧结而成，因此具有多孔性，有助于增大内部接触面积，提高电容容值。Ta2O5介质通过阳极氧化，形成于阳极Ta的外表面。将钽棒浸入锰盐溶液中并热分解，形成阴极MnO2。钽电容的结构如图1所示。

1.2 钽电容实验测试

钽电容用于智能引信中，需要经受瞬间强冲击载荷的作用，在冲击载荷作用下钽电容性能的变化为其电容量和漏电电流的变化。马歇特锤试验装置能够产生瞬态冲击载荷，载荷范围在0～50 000g之间，能够在试验中模拟钽电容的实际使用工况。因此，使用马歇特锤击设备测试钽电容的电容量和漏电流。实验过程中，选取4种不同类型的钽电容进行测试，将被测钽电容焊接在电路板上，电路板采用螺纹连接与击锤固定在一起。击锤安装于固定在偏心轮的锤杆上。实验时使用偏心轮将击锤升至一定高度，用卡齿固定。卡齿放开后，依靠偏心轮下方的重锤作为动力，击锤击打在铁锭上产生冲击载荷。使用压电式加速度计实时记录冲击过载值。使用漏电流测试仪(Keithley 6487 Picoammeter)监测钽电容漏电流随冲击作用的变化，动态信号分析仪记录皮安表输出。使用阻抗分析仪(Agilent 4294A)记录电容量的变化。传感器型号为PCB 350B21，灵敏度为0.05 mV/g，量程为±100 000g。在电容充电5 min后进行实验，实验过程中，采用步进冲击方法，逐步增大冲击g值，观察钽电容电参数的变化。实验系统如图2所示。钽电容参数及测量范围如表1所示。

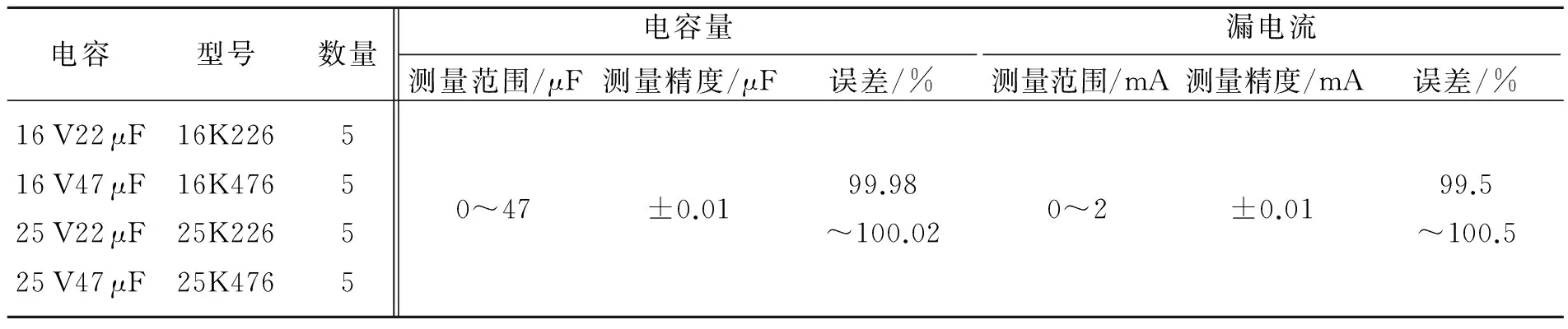
电容型号数量电容量测量范围/μF测量精度/μF误差/%漏电流测量范围/mA测量精度/mA误差/%16V22μF16V47μF25V22μF25V47μF16K22616K47625K22625K47655550^47±0.0199.98^100.020^2±0.0199.5^100.5

2 实验结果

图3为钽电容的额定电容随冲击载荷变化的情况。从实验结果发现，电容量随冲击载荷的变化而发生变化。对于16 V22 μF钽电容，在施加1 000g冲击后，电容量有0.1 μF的升高；持续增加冲击载荷，在3 000g时电容量增加0.15 μF；当冲击值达到10 000g时，电容量升高0.4 μF对于16 V47 μF钽电容，在施加1 000g冲击后，电容量有0.15 μF的升高；在3 000g时电容量增加0.2 μF；当冲击值达到10 000g时，电容量升高0.45 μF。对于25 V22 μF钽电容，与冲击载荷对应的电容量变化为0.12、0.17和0.45 μF；对于25 V47 μF，电容量对应的变化为0.13、0.19和0.50 μF。冲击完成后，电容量恢复至原来的额定值。

图4为漏电流随冲击载荷的变化情况。电容接通电源后，涌入的电流为充电电流，充电电流开始很大，随着时间延长(≥5 min)而下降稳定在远小于额定电流的特定值，此时的电流为漏电流。实验过程中，冲击值从1 000g开始逐渐增加。从实验结果发现，漏电流变化趋势与冲击载荷变化相一致。对于16 V22 μF电容施加1 000g的冲击后，漏电流增加一个数量级，当冲击值增加到3 000g时，漏电流约为0.15 mA，随着冲击值的增大，漏电流逐渐增加。当冲击值达到10 000g时，漏电流达到0.25 mA。对于16 V47 μF电容，施加1 000g的冲击后，漏电流达到0.28 mA，当冲击值增加到3 000g时，漏电流约为0.4 mA，当冲击值达到10 000g时，电容漏电流达到0.6 mA。对25 V22 μF电容施加1 000g的冲击后，漏电流约为0.13 mA，当冲击值增加到3 000g时，漏电流约为0.44 mA，当冲击值达到10 000g时，漏电流达到0.9 mA。对于25 V47 μF电容，施加1 000g的冲击后，漏电流达到0.4 mA，当冲击值增加到3 000g时，漏电流约为0.6 mA，当冲击值达到10 000g时，电容漏电流达到1.7 mA。

如图4所示，当冲击载荷结束后，4组钽电容的漏电流经过一段时间后恢复到原始水平。即使漏电流达到很高的量级，在钽电容未被击穿时，冲击过后，漏电流依然能恢复到原来的水平。这种特性称为钽电容的自愈特性。

智能引信能够引爆战斗部，要求钽电容中存储的能量必须大于电雷管的安全起爆能量。由于钽电容在冲击载荷作用下漏电流增大，则电容中储存的能量以漏电流的形式出现损耗。当钽电容剩余的能量大于电雷管需要的发火能量时，才能可靠引爆电雷管，可靠实现智能引信的功能。

图5为引信点火电路[6]，其中电雷管起爆所满足的条件为：

(1)

针对钽电容允许的最大漏电流，继续加大冲击应力，得出与钽电容对应的临界失效冲击载荷，如图6所示。

由图6可知，钽电容漏电流在冲击载荷作用下呈指数型升高。钽电容临界失效载荷及钽电容漏电流在冲击载荷下的变化模型如表2所示。

表2 漏电流-冲击模型 Table 2 Numerical model of leakage current-shock load

3 电参数变化机理分析

由实验结果可知，冲击会引起钽电容电参数的变化：电容量的升高及漏电流随冲击载荷的升高呈指数型升高。分析钽电容电参数变化，可得冲击载荷对钽电容的作用机理为：弹性变形范围内，冲击引发的钽电容变形导致电容的变化；冲击引起介质层微裂缝以及冲击引起陷阱能级的升高导致漏电流增大。

3.1 冲击引起的钽电容变形

由于钽电容是由钽颗粒压制烧结而成，因此钽电容可以看做多个钽颗粒电容的并联。图7为单个钽颗粒模型。钽电容在受到冲击载荷作用时，赋能颗粒发生变形，在弹性变形范围内，由球形颗粒变形为椭球形颗粒，然后恢复原状。

图7(a)所示的球形电容的电容量为：

Cs=4πεRr/(R-r)

(2)

式中：ε为介电常数,F/m；R为Ta2O5外径,mm；r为Ta半径,mm。图7(b)所示椭球型电容的电容量为[7]：

(3)

式中：Q为电荷量,C；U为内外极板之间的电压,V；w为变形量,mm。

在冲击过程中，电容的变化量为：

(4)

冲击作用下球形颗粒的变形见图8。根据赫兹接触理论得，在力F(t)作用下，在弹性变形范围内，两球心O1、O2相互接近的距离为：

(5)

式中：R1、R2为两球的半径，μ1、μ2、E1和E2分别为泊松比及弹性模量，GPa。

则电容球形颗粒在受到冲击作用时，球心相互接近的距离为：

δ3=9F2(t)(1-μ2)/(4RE2)

(6)

则单个球形颗粒变形量为：

(7)

在冲击作用下，电容值的变化量为：

(8)

图9为钽颗粒电容随冲击载荷的变化。

假设钽电容由半径均匀一致的球体钽颗粒电容组成，则每个钽电容所包含的球形电容的数量N为：

N=V/∑Vi

(9)

式中：V为未封装的钽电容体积，Vi为Ta、Ta2O5、MnO2的体积。不同类型钽电容包含球形钽颗粒电容的数量及电容变化值如表3所示,图10为不同类型电容与冲击载荷的关系。

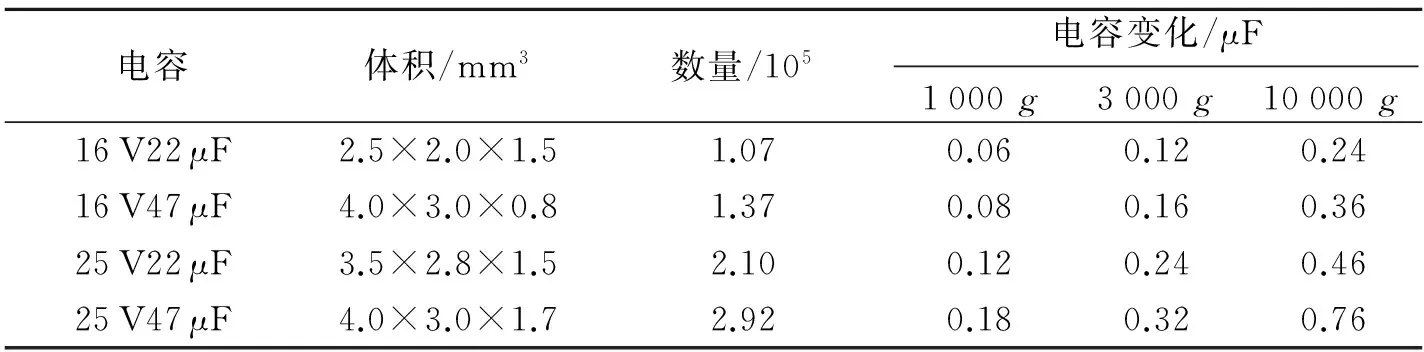
电容体积/mm3数量/105电容变化/μF1000g3000g10000g16V22μF2.5×2.0×1.51.070.060.120.2416V47μF4.0×3.0×0.81.370.080.160.3625V22μF3.5×2.8×1.52.100.120.240.4625V47μF4.0×3.0×1.72.920.180.320.76

由表3可知，计算值与实验值存在偏差。分析可知造成数值偏差的原因为：由于加工钽电容时，在外层添加石墨和银层，而在计算时，忽略石墨和银层，造成数值出现偏差；钽电容变形时，不仅在纵向出现变形，横向同样存在微小形变，计算时未考虑横向变形因素。

3.2 冲击引起的漏电流变化

冲击引起的漏电流变化是由两种机制决定的：介质层在冲击下产生微裂缝；冲击下电子陷阱的产生，Ta—O化合键的断裂以及氧气空穴的产生。陷阱浓度的增加使参与导电的电子增多，漏电流从而增大。

实验中发现，在钽电容未被击穿时，冲击过后，漏电流依然能恢复到原来的水平。这种现象可由钽电容的自愈机理解释。在冲击载荷作用下，钽电容介质层产生“薄弱”区，使该区域漏电流增大。持续增大的电流使局域温度升高，当温度达到400 ℃时，导电性良好的MnO2转变为导电性能差的Mn2O3，覆盖到缺陷区域上，使“薄弱”区域处的漏电流恢复至原来的量级。

4 结 论

利用马歇特落锤实验对固体钽电容进行高过载测试，从测试结果发现，冲击载荷对固体钽电容电参数的影响主要表现为电容量的升高以及漏电流的增大。电容量随着冲击载荷的增加而增加，钽电容漏电流随冲击载荷的升高呈指数型升高，冲击过后，电容量恢复额定容值，经过一段时间，钽电容漏电流同样恢复至原来的量级。同时，分析钽电容电参数变化原因，得出引起钽电容电参数变化的机制为：冲击引起的钽电容的弹性变形使电容量增大，冲击引起的介质层Ta2O5中的微裂缝以及冲击引发的介质层陷阱浓度的变化。钽电容球形模型在冲击载荷作用下发生弹性变形，使电容量发生改变。在冲击载荷的作用下，介质层缺陷处容易引发微裂缝，形成导电微沟道，使漏电流增大。另外，由于冲击载荷的作用使介质层中化合键产生断裂导致电子传导机制中参与导电的电子增多，同时由于氧空穴在Ta2O5和MnO2界面处的积累，使界面产生极化，界面势垒降低进而导致注入的电子数量增多，电流密度增大，漏电流升高。

[1] 徐建军.高冲击高温下电引信关键元器件可靠性测试[J].弹箭与制导学报,2011,31(1):151-152.

XU Jianjun. Reliability test of key components of electric fuze subjected to high impact and high temperature[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011,31(1):151-152.

[2] TEVEROVSKY A. Effect of mechanical stresses on characteristics of chip tantalum capacitors[J]. IEEE Transactions on Device and Materials Reliability, 2007,7(3):399-406.

[3] TEVEROVSKY A. Effect of reverse bias stress on leakage currents and breakdown voltages of solid tantalum capacitors[R]. Greenbelt, MD: NASA Goddard Space Flight Center, 2011.

[4] 程融,张永录.某型电子干扰弹引信用固体钽电容器失效分析[J].国防技术基础,2009(8):28-30.

CHENG Rong, ZHANG Yonglu. Failure analysis of solid tantalum capacitors used for electronic jamming bombs fuse[J]. Technology Foundation of National Defence, 2009(8):28-30.

[5] 何荣华,张亚,李波,等.高过载下军用电容的参数变化研究及失效分析[J].电子产品可靠性与环境试验,2010,28(1):24-26.

HE Ronghua, ZHANG Ya, LI Bo, et al. Parametric variation and failure analysis of military capacitors under high overload[J]. Electronic Product Reliability & Environmental Testing, 2010,28(1):24-26.

[6] 景义林.旋转椭球形电容器的电容与静电能[J].大学物理,2011,30(10):25-27.

JING Yilin. The capacitance and electrostatic energy of a revolving ellipsoidal capacitor[J]. College Physics, 2011,30(10):25-27.

[7] CHIU F C. A review on conduction mechanisms in dielectric films[J]. Advances in Materials Science & Engineering, 2014,2014(7):1-18.