孔间距对燃气轮机动叶气膜冷却效果的影响

唐学智， 李录平， 黄章俊， 梁永纯， 钟万里

(1.长沙理工大学 能源与动力工程学院，长沙 410014；2.广东电网有限责任公司电力科学研究院，广州 510080)

现代重型燃气轮机透平入口温度已经远远超过金属材料所能承受的范围，必须结合先进的热障涂层和多种冷却技术，来保证这些热端部件在高温下的正常运行和工作寿命.提高透平入口温度是改善燃气轮机效率的重要途径，但目前叶片材料的研究受到了很大限制，因此有效的冷却措施对透平叶片显得尤为重要[1].气膜冷却技术经过几十年的发展，已被广泛应用于燃气轮机热端部件，成为透平叶片的重要冷却方式之一.影响气膜冷却效率的因素大致分为2类[2-3]：一是流动参数，如吹风比、密度比和主流湍流度等；二是结构参数，如孔径大小、孔间距、孔形状和小孔与壁面的夹角等.国内外学者主要采用实验和数值模拟方法对这2类因素进行研究.

实验研究方面，Ito等[4]在早期利用热电偶测温方法对单孔和孔排三维气膜冷却的传热系数进行了研究.Schwarz等[5]利用传质类比的方法在曲面上研究了不同吹风比对冷却性能的影响，实验结果显示凸面上的冷却效率要高于平板和凹面上的冷却效率.高媛等[6-8]采用实验方法对气膜冷却特性进行研究，获得了大量的实验数据，完善了气膜冷却机理.

随着计算机技术的不断发展，采用数值模拟方法研究气膜冷却的流动与传热得到了广泛应用.Dring等[9]在低速旋转动叶模型上研究了吹风比对叶片局部气膜冷却效率的影响，并与平板气膜冷却的实验结果进行了对比，结果表明数值模拟结果与实验研究误差相差不大.李少华等[10]采用Realizablek-ε紊流模型并结合Simplec算法对动叶栅在不同转速下的气膜冷却效率进行计算，结果表明旋转导致冷却射流向叶顶偏移，转速越高气膜冷却效率越低.张玲等[11-12]对动叶全表面气膜冷却进行了数值模拟，研究了叶片在不同吹风比条件下叶片表面的能量损失.

综上所述，大多数的研究对象都是平板模型和放大计算模型[13-14]，很少有针对实际涡轮叶片三维实体模型进行的数值模拟.笔者采用数值模拟方法对某重型燃气轮机透平第一级动叶进行气膜冷却效率研究，分析了孔间距对叶片气膜冷却效率的影响，旨在为涡轮叶片气膜冷却结构设计提供理论依据.

1 描述气膜冷却过程的基本模型

1.1 气膜冷却过程物理模型

叶片在工作过程中具有周期性，因此选取单个叶栅通道进行气膜冷却数值模拟.图1中，主流高温气体(以下简称主流)从入口流入，通过叶片后从出口流出，形成一个高温流域.而射流冷却气体(以下简称射流)从叶片底部7个锥形通道流入，部分冷却气体通过叶片表面小孔流出后被主流压弯，贴着叶片壁面流动，形成气膜层，避免主流与叶片壁面直接接触；另一部分通过叶顶小孔流出，而后汇入主流.在这一流动过程中，射流与主流之间进行了大量的能量交换和质量传递，其流动过程相当复杂，影响因素众多.因此，为了方便研究，对该过程进行简化，叶片与流体之间的传热只考虑对流换热，壁面均采用无滑移壁面条件，上下两侧为绝热壁面，主流两侧为周期性边界条件[15-16].

图1 气膜冷却过程

1.2 气膜冷却过程的湍流模型

气膜高速流动过程中，流动形式为湍流，采用雷诺平均N-S方程中的连续方程、动量方程和能量方程来描述其流动过程，表达式[17]如下：

(1)

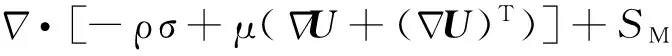
(2)

(3)

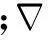
Realizablek-ε湍流模型在标准k-ε模型的基础上进行了一些改进，此处采用Realizablek-ε湍流模型，其湍动能及耗散率运输方程[17]为：

(4)

(5)

在Fluent中，作为默认值常数，C1ε=1.44，C2=1.9，σk=1.0，σε=1.2.

2 气膜冷却过程的计算方法

2.1 几何模型及网格生成

参考某重型燃气轮机透平第一级动叶结构参数建立相应的三维实体模型(见图2(a)).叶片弦长为108.75 mm，叶高为171.58 mm，安装角为59.28°.叶片为气膜孔全覆盖模型(见图2(c))，其中前缘5排孔，压力面6排孔，吸力面5排孔，各排孔之间采用交错插排的排列方式，目的是使冷却气体更均匀地覆盖在叶片表面形成气膜，隔离高温燃气，保护叶片.笔者将叶片尾缘劈缝和内部结构简化成几个单独的冷却通道，由于所采用的数值模拟设置为稳态流动，因此这样的简化并不会给计算带来很多误差，且有利于对叶片整体气膜冷却的分析.

由于叶片表面有多排密集的冷气喷射孔覆盖，且冷却孔的结构、入射角度和排列方式都有很大区别，这些都给网格划分造成很大的困难.因此选用Ansys ICEM作为计算域的网格划分软件，采用结构化与非结构化相结合方式，结构化网格部分形式采用分块结构化网格(Multi-Block Structured Mesh).对重点区域进行了网格加密处理，而对叶片型面的不规则性采用interface来融合网格，合理规划整个计算区域的网格分布，其中气膜孔内的网格数超过2×105，网格总数大于9.9×106，气膜孔出口所在平面的y+都小于5，满足计算要求.

图3给出了吹风比M=0.6时，对网格进行进一步加密后计算结果的比较，所提取的数据为孔间距S/d=4时压力面孔排6下游处沿射流方向的气膜冷却效率η，其中原点表示孔排中心位置，X为气膜孔中心至测量点的叶片表面相对距离，d为孔径，X/d为二次流与主流混合的归一化长度.从图3可以看出，使用3种网格数所计算出的冷却效率非常接近，最大误差小于3%，说明所采用的网格无关性很好.

(a) 三维实体叶片模型

(b) 内部冷却通道分布

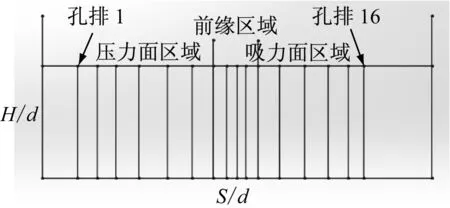
(c) 叶片表面展开图(孔排1～孔排16)

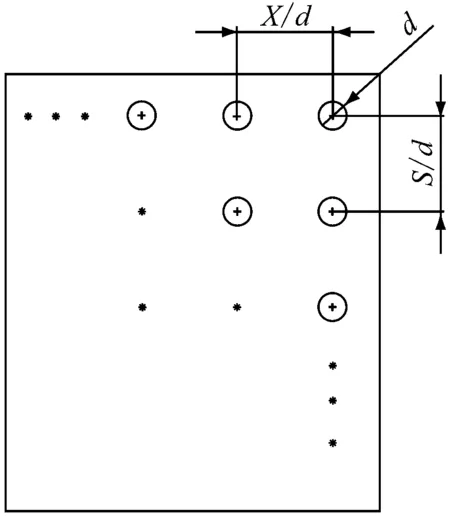
(d) 叶片表面孔排示意图

图3 网格无关性检验

2.2 边界条件

采用加强壁面函数法处理近壁区的流动，假定在壁面处无滑移，叶片表面为绝热表面，入口雷诺数Re计算方法为：

Re=Ud/υ

(6)

式中：U为流体流速，m/s；υ为运动黏度，m2/s.

计算域的两侧为周期性边界条件，其他壁面均设置为绝热壁面，主流入口设定为压力入口，入口总压为1 671 180 Pa，温度为1 593.15 K；气体出口设为压力出口，出口压力为831 430 Pa.射流温度为723.15 K，通过改变射流入口压力，可得到不同的吹风比M，主流与射流的密度比DR=2.

2.3 评价冷却效果的基本指标

采用以下5个指标来评价气膜对叶片金属的冷却效果.

(1) 吹风比M.

吹风比[17]定义为：

(7)

式中：ρc和ρ∞分别为射流与主流的密度，kg/m3.Uc和U∞分别为射流与主流的流速，m/s.

吹风比实质就是射流与主流的质量流量之比，吹风比越大，表示射流质量流量越大.

(2) 气膜冷却效率η.

气膜冷却效率[17]定义为：

(8)

式中：T∞为主流气体温度，K；Taw为绝热壁面温度，K；Tc为射流气体温度，K.

η是衡量气膜冷却特性的一个重要参数，η值越高，表明壁面附近的流体温度越接近于二次流温度.

(3) 气膜有效覆盖比Af.

在进行气膜冷却时，一般要求气膜在冷却壁面上能均匀且分布广泛.因此，有效的气膜覆盖面积成为考察气膜冷却好坏的重要因素，为此定义气膜有效覆盖比Af[18]为：

(9)

式中：af为有效气膜覆盖面积，m2；ah为冷却工质输送通道的横截面积，m2，

气膜的有效覆盖是指η≥0.2的区域，通过计算气膜有效覆盖比Af，能够更好地从整体上判断气膜冷却的好坏.

在气膜有效覆盖范围内，平均气膜冷却效率[14]定义为：

(10)

(5) 不均匀系数β.

不均匀系数β是用来考察气膜覆盖均匀性的，其定义式[18]为：

(11)

从式(11)可以看出，不均匀系数就是一个方差值，β值越小表示气膜覆盖越均匀.

3 计算结果与分析

3.1 冷却效率随吹风比的变化

3.1.1 压力面的影响

图4给出了孔间距S/d=2，湍流度Tu=5%时叶片压力面气膜冷却效率分布云图.从图4可以看出，在其他条件不变的情况下，随着吹风比的增大，压力面的孔排下游区域冷却效率得到明显提高.M=0.6时，冷却射流从气膜孔流出，动量小，冷气覆盖区域也小，η偏低；当M=1.4时，冷却射流动量增大，相互间影响作用也越大，受主流的影响不断减小，在图上出现了气膜孔排下游的高冷却效率区域.同时可以发现，在一定吹风比下，η沿流向呈现上升趋势.这是由于在前几排气膜孔冷却射流动量小，与主流掺混后很容易被主流射穿直接对叶片壁面加热；而后缘气膜孔流出的冷却气体沿程不断累积，使得后缘冷却射流动量不断增大，主流气体难以射穿气膜层.因此，后缘的气膜冷却效率要明显高于前缘.

(a) M=0.6

(b) M=1.0

(c) M=1.4

Fig.4 Distribution of film cooling efficiency on pressure surface for hole spacingS/d=2

图5给出了S/d=2时吹风比对压力面孔排6和孔排1气膜冷却效率的影响.从图5可以看出，不管是在压力面前缘还是后缘，沿孔排下游区域气膜冷却效率都呈现下降的趋势.这是由于冷却射流从气膜孔流出后，与主流的掺混作用不断加强，冷却射流动量不断减小，主流在后缘更容易穿透气膜层对壁面进行加热，因此气膜冷却效率更低.在X/d<5时，曲线的斜率最大，气膜冷却效率下降得最快.同时可以看到，当吹风比M=1.4，X/d>5时曲线趋于水平，说明在高吹风比下，冷却射流在孔排下游能形成有效保护膜，能够很好地保护孔排下游区域，尤其是叶片尾缘范围.

(a) 孔排6

(b) 孔排1

Fig.5 Effect of blowing ratio on film cooling efficiency through holes in row 6 and row 1 on pressure surface for hole spacingS/d=2

图6给出了孔间距S/d=4，湍流度Tu=5%时，不同吹风比下压力面气膜冷却效率分布云图，其影响规律与孔间距S/d=2时大致相同，随着吹风比的增大，叶片压力面综合冷却效率不断提高.对比图4可以发现，在吹风比一定的情况下，随着孔间距的增大，气膜冷却效率呈现明显的下降趋势，这是由于当孔间距S/d=2时，气膜孔之间的间距较小，在孔下游及孔间区域发生强烈的气膜干扰，使得孔排下游冷却射流分布均匀，对下游区域形成很好的保护作用，气膜冷却效率较高；而孔间距S/d=4时，孔间距较大，孔间作用减弱，导致孔间存在气膜冷却效率较低的点，但在孔下游区域仍然能够形成一定的保护作用.

(a) M=0.6

(b) M=1.0

(c) M=1.4

Fig.6 Distribution of film cooling efficiency on pressure surface for hole spacingS/d=4

图7给出了S/d=4吹风比对压力面孔排6和孔排1气膜冷却效率的影响.对比图7和图5可以看出，同一吹风比下，相同位置的气膜冷却效率都呈现降低趋势，但是在不同吹风比下影响规律并不相同.图7(a)中，当X/d>15，M=1.0与M=1.4的2条曲线基本重合，这表示在叶片前缘，当吹风比达到1.0后，继续增大吹风比对气膜冷却效率影响不大；而图7(b)中，X/d<5范围内3根曲线有交叉点，M=0.6曲线在接近X/d=0位置要高于M=1.4曲线，这是由于在低吹风比时，低动量冷却射流从气膜孔流出后更易于贴近壁面，形成气膜层；而在高吹风比时，高动量的冷却射流更容易穿透主流，在孔下游附近才能形成气膜层.而当X/d>10后，高吹风比的气膜冷却效率明显要高于低吹风比的冷却效率，这与图5的规律基本相似.

(a) 孔排6

(b) 孔排1

Fig.7 Effect of blowing ratio on film cooling efficiency through holes in row 6 and row 1 on pressure surface for hole spacingS/d=4

3.1.2 吸力面的影响

图8中，在其他条件不变的情况下(S/d=2，Tu=5%)，随着吹风比的增大，吸力面综合气膜冷却效率得到相应提高.这一规律与压力面相似，且由于冷却射流的叠加效果，叶片后缘的气膜冷却效率要明显高于前缘.从图9可以看出，当吹风比M从0.6增大到1.0时，气膜冷却效率的增长幅度要大于吹风比M从1.0增大到1.4过程.这说明同一孔间距下，随着吹风比的增大，吸力面的综合冷却效率增长幅度在减小.因此，在同一孔间距条件下应该对应一个最佳吹风比.

图10给出了孔间距S/d=4，湍流度Tu=5%时吸力面气膜冷却效率分布云图.对比图10和图8可知，在吹风比不变的情况下，随着孔间距的增大，气膜冷却效率呈明显的下降趋势.其原因在于随着孔间距的增大，相邻气膜孔之间的相互作用减小，主流对冷却气体的掺混作用力加强，因此孔间距S/d=4时吸力面气膜冷却效率明显降低.

图11给出了吹风比对吸力面孔排12和孔排16 气膜冷却效率的影响.图11(a)中，当吹风比M=0.6时，曲线呈现一个逐步衰减的趋势；而吹风比M=1.0和1.4时，曲线在X/d<10内呈现增大趋势，而后趋于平缓.这是由于当吹风比M=0.6时，冷却气体从气膜孔流出后，动量很小，能够很好地覆盖在叶片表面，受到主流的掺混作用力，气膜冷却效率逐渐降低；当吹风比M=1.0时，冷却气体从气膜孔流出后，由于吸力面形状为凸型，高动量的射流易射穿主流，随着其与主流掺混作用加强，在很短时间内被主流压弯，对气膜孔下游形成保护.后缘趋于平缓是由于叶片前缘气膜孔冷却气体形成叠加作用，使得后缘能够形成有效的保护膜.图11(b)中，当X/d>20时，M=1.0与M=1.4曲线基本重合，说明在吸力面后缘，吹风比的增大对气膜冷却效率的影响在逐渐减弱.

(a) M=0.6

(b) M=1.0

(c) M=1.4

Fig.8 Distribution of film cooling efficiency on suction surface for hole spacingS/d=2

(a) 孔排12

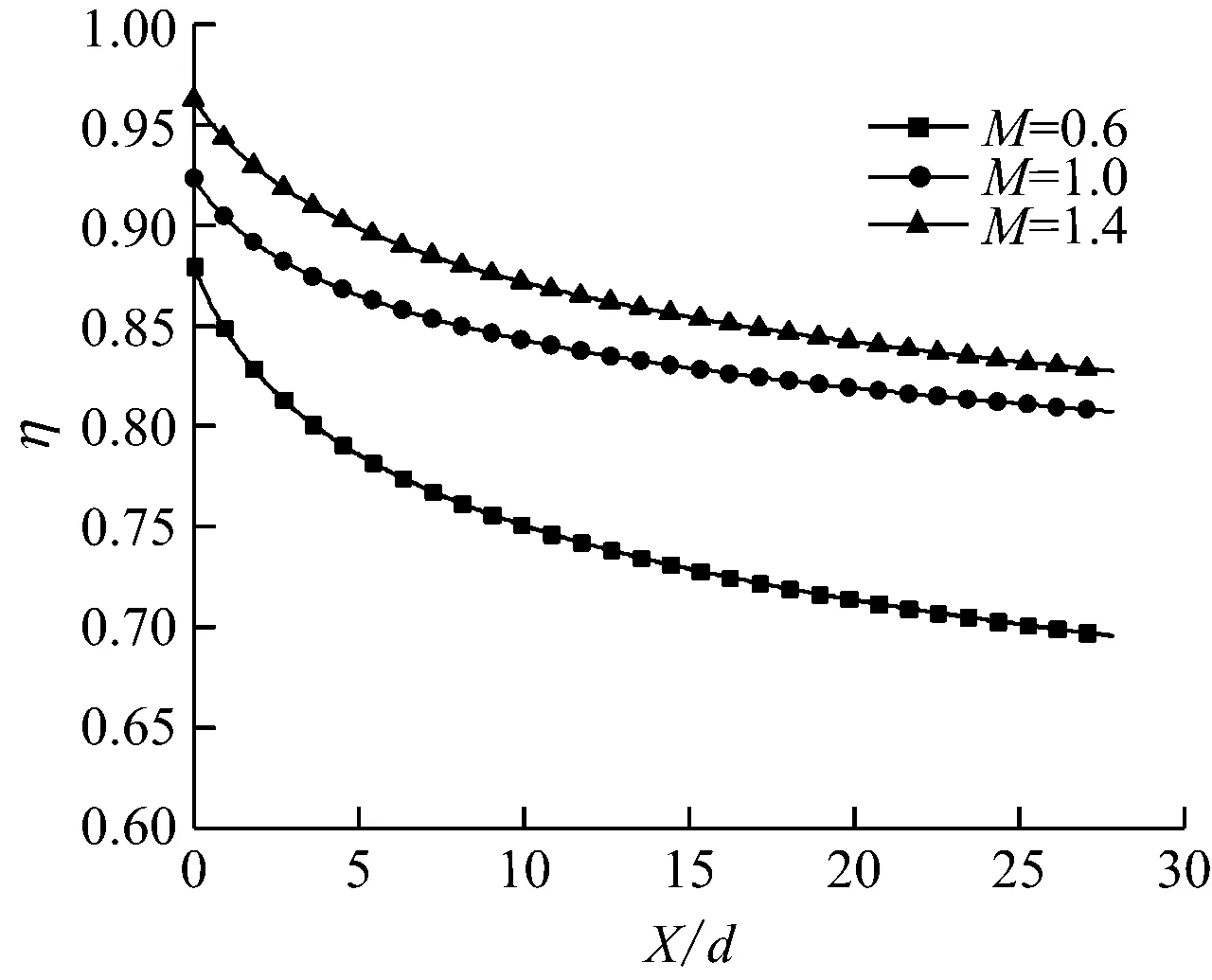
(b) 孔排16

Fig.9 Effect of blowing ratio on film cooling efficiency through holes in row 12 and row 16 on suction surface

(a) M=0.6

(b) M=1.0

(c) M=1.4

Fig.10 Distribution of film cooling efficiency on suction surface for hole spacingS/d=4

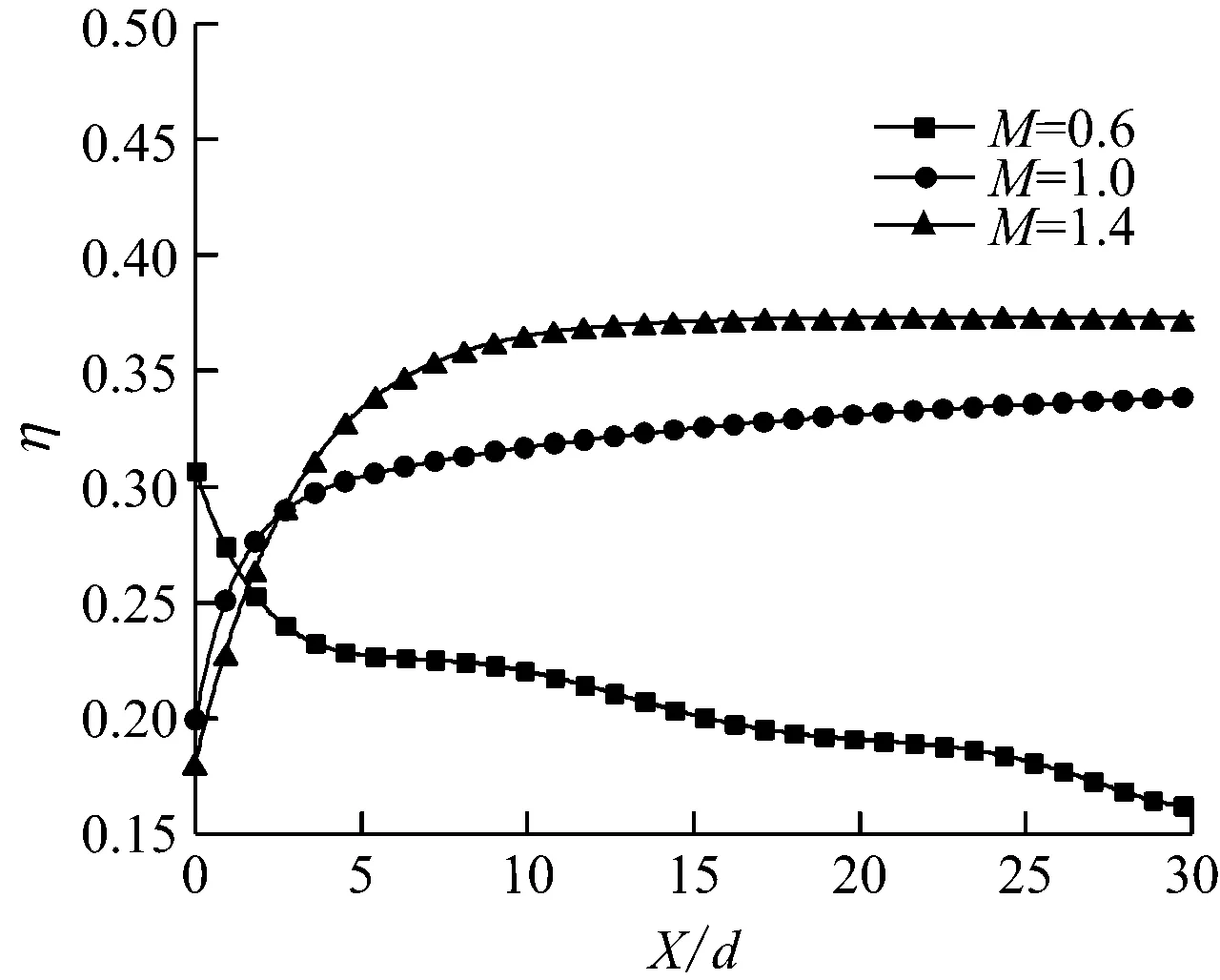
(a) 孔排12

(b) 孔排16

Fig.11 Effect of blowing ratio on film cooling efficiency through holes in row 12 and row 16 on suction surface

3.1.3 气膜冷却效果总性能对比

表1不同孔间距下叶片的气膜冷却效果

Tab.1Filmcoolingeffectivenessfordifferentholespacing

MAfηβS/d=2S/d=4S/d=2S/d=4S/d=2S/d=40.630.5640.630.530.340.130.191.038.2648.630.620.410.110.141.444.5653.460.680.460.100.12

3.2 主流湍流度对冷却效率的影响

图12给出了吹风比M=1.4时，孔间距S/d=2和4时叶片压力面在不同主流湍流度下冷却效率的分布云图.从图12可以看出，当吹风比M=1.4时，在同一孔间距条件下，主流湍流度越小，冷却效率越高.这是由于主流湍流度增大后，其与冷却气体的掺混作用加强，使得冷却效率下降，但影响较小.随着孔间距的减小，主流湍流度对气膜冷却效率的影响也越明显.

(a) Tu=5%,S/d=4

(b) Tu=0.5%,S/d=4

(c) Tu=5%,S/d=2

(d) Tu=0.5%,S/d=2

Fig.12 Distribution of film cooling efficiency on pressure surface for blowing ratioM=1.4

图13给出了吹风比M=1.4时叶片压力面后缘孔排气膜冷却效率分布云图.从图13可以看出，不同孔间距下，主流湍流度的改变对气膜冷却效率的影响不一样.当孔间距S/d=4时，高主流湍流度下的冷却效率在气膜孔附近区域低于低主流湍流度下的冷却效率，但在X/d>10后趋于相同，甚至要高于低主流湍流度时，这是由于在中下游区域，加速流动的主流在高湍流度下使得冷气的贴壁性更好.而孔间距S/d=2时，低主流湍流度下的的气膜冷却效率一直高于高主流湍流度下的气膜冷却效率.

图14给出了吹风比M=1.4时，叶片吸力面气膜冷却效率分布云图.从图14可以看出，同一孔间距下，低主流湍流度下的综合冷却效率值略高于高主流湍流度下的综合冷却效率值.这是由于吸力面本身形状是凸型，吹风比M=1.4时，冷却气体从气膜孔流出后易穿透主流，在高主流湍流度下与主流的掺混作用加强，因此气膜冷却效率下降.

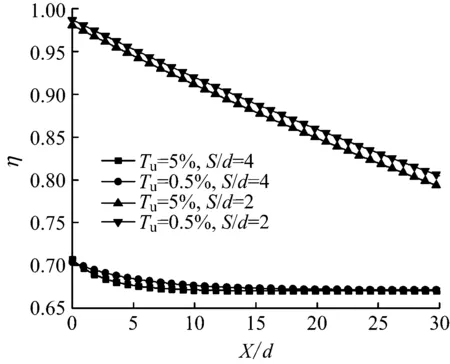
图13 吹风比M=1.4时叶片压力面后缘孔排气膜冷却效率分布

Fig.13 Distribution of exhaust film cooling efficiency at trailing edge on pressure surface for blowing ratioM=1.4

(a) Tu=5%,S/d=4

(b) Tu=0.5%,S/d=4

(c) Tu=5%,S/d=2

(d) Tu=0.5%,S/d=2

Fig.14 Distribution of film cooling efficiency on suction surface for blowing ratioM=1.4

图15给出了吹风比M=1.4时，叶片吸力面后缘孔排气膜冷却效率分布云图.从图15可以看出，孔间距S/d=4时，叶片吸力面后缘孔排气膜冷却效率呈现升高趋势，这是由于前排孔冷气的动量叠加效果，使得后缘孔排的气膜冷却效率值升高.当孔间距S/d=2时，孔间距较小，空间作用加强，叠加效果就会显得不那么明显，由于冷却气体动量更大，与主流的掺混作用也更剧烈，因此呈现降低趋势.总体来讲，主流湍流度对气膜冷却效率的影响不大.

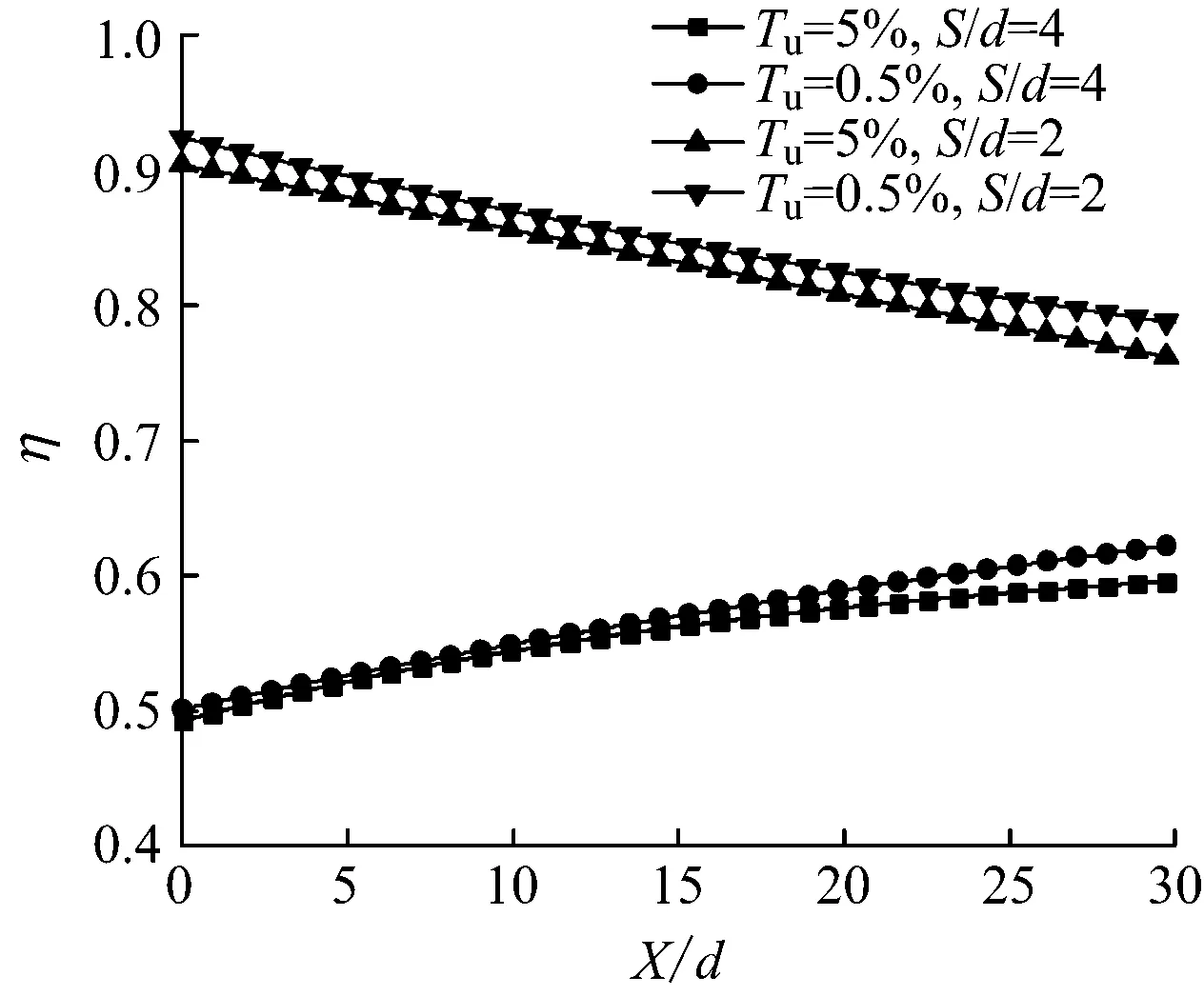
图15 吹风比M=1.4时叶片吸力面后缘孔排气膜冷却效率分布

Fig.15 Distribution of exhaust film cooling efficiency at trailing edge on suction surface for blowing ratioM=1.4

4 结 论

(1) 相同吹风比条件下，随着孔间距的增大，冷却气体覆盖程度变差，气膜冷却效率下降.受到叶片前缘孔排冷却气体的动量叠加，叶片后缘冷气覆盖程度好，气膜冷却效率明显高于前缘.

(2) 相同孔间距条件下，随着吹风比的增大，叶片综合冷却效率呈现升高趋势.孔间距S/d=2时，叶片前缘孔排和后缘孔排气膜冷却效率分布规律基本一致，孔间距S/d=4时，叶片前缘孔排与后缘孔排分布规律有所不同，吸力面后缘孔排气膜冷却效率沿主流流向呈现升高趋势.

(3) 当吹风比M=1.4时，主流湍流度越大，其与主流的掺混能力越强烈，因此气膜冷却效率越低，但影响较小.

[1] ERIKSEN V L. Film cooling effectiveness and heat transfer with injection through holes[R]. [S.l.]: NASA, 1971.

[2] BALDAUF S, SCHEURLEN M, SCHULZ A, et al. Correlation of film-cooling effectiveness from thermographic measurements at enginelike conditions[J].JournalofTurbomachinery, 2002, 124(4): 686-698.

[3] 范小军, 杜长河, 李亮, 等. 气膜孔几何位置对旋流冷却流动与传热特性的影响[J].西安交通大学学报, 2016, 50(7): 32-38.

FAN Xiaojun, DU Changhe, LI Liang, et al. Effect of bleed hole location on vortex cooling flow and heat transfer performance[J].JournalofXi′anJiaotongUniversity, 2016, 50(7): 32-38.

[4] ITO S, GOLDSTEIN R J, ECKERT E R G. Film cooling of a gas turbine blade[J].JournalofEngineeringforPower, 1978, 100(3): 476-481.

[5] SCHWARZ S G, GOLDSTEIN R J, ECKERT E R G. The influence of curvature on film cooling performance[J].JournalofTurbomachinery, 1991, 113(3): 472-478.

[6] 高媛, 葛利顺, 王宏光, 等. 振动平板单孔气膜冷却实验研究[J].动力工程学报, 2016, 36(9): 704-710.

GAO Yuan, GE Lishun, WANG Hongguang, et al. Experimental study on single-hole film cooling effectiveness over vibrating plates[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(9): 704-710.

[7] AL-ZURFI N, TURAN A, NASSER A. Numerical investigation of rotation effects on anti-vortex film-cooling holes[J].Flow,TurbulenceandCombustion, 2016, 96(1): 133-162.

[8] 常艳, 杨卫华, 张靖周. 突片形状对气膜冷却效率的影响[J].南京航空航天大学学报, 2016, 48(3): 317-325.

CHANG Yan, YANG Weihua, ZHANG Jingzhou. Effects of tab shapes on film cooling effectiveness[J].JournalofNanjingUniversityofAeronautics&Astronautics, 2016, 48(3): 317-325.

[9] DRING R P, BLAIR M F, JOSLYN H D. An experimental investigation of film cooling on a turbine rotor blade[J].JournalofEngineeringforPower, 1980, 102(1): 81-87.

[10] 李少华, 李知骏, 王梅丽, 等. 旋转对复合角度气膜冷却叶片的数值模拟[J].汽轮机技术, 2011, 53(3): 164-166.

LI Shaohua, LI Zhijun, WANG Meili, et al. Numerical simulation study on the effect of rotation on film cooling of blades with compound angle holes[J].TurbineTechnology, 2011, 53(3): 164-166.

[11] 张玲, 修栋波, 汪山入. 化工燃气轮机动叶全表面气膜冷却影响的数值模拟[J].化工机械, 2016, 43(2): 186-193.

ZHANG Ling, XIU Dongbo, WANG Shanru. Numerical simulation of unsteady wakes′ effect on film cooling of rotor blade surface[J].ChemicalEngineering&Machinery, 2016, 43(2): 186-193.

[12] 林晓春, 刘建军. 透平叶栅气膜冷却损失分析[J].工程热物理学报, 2016, 37(8): 1627-1634.

LIN Xiaochun, LIU Jianjun. The loss analysis of film cooling on turbine vane cascade[J].JournalofEngineeringThermophysics, 2016, 37(8): 1627-1634.

[13] 戴萍, 林枫. 孔间距对缩放槽缝孔气膜冷却效率的影响[J].汽轮机技术, 2010, 52(3): 191-194, 214.

DAI Ping, LIN Feng. Influence of hole pitch on film cooling effectiveness from converging slot-hole[J].TurbineTechnology, 2010, 52(3): 191-194, 214.

[14] 戴萍. 气膜孔几何结构对涡轮叶片气膜冷却的影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.

[15] 于飞龙, 上官博, 李园园, 等. 重型燃气轮机透平第一级动叶复合冷却数值研究[J].中国电机工程学报, 2016, 36(1): 179-186.

YU Feilong, SHANGGUAN Bo, LI Yuanyuan, et al. Numerical investigation on compound cooling effect of the heavy-duty gas turbine first stage blade[J].ProceedingsoftheCSEE, 2016, 36(1): 179-186.

[16] 蒋文程, 赵志军, 李树元. 叶片前缘上游端壁气膜冷却试验研究[J].动力工程学报, 2016, 36(3): 191-195, 226.

JIANG Wencheng, ZHAO Zhijun, LI Shuyuan. Experimental study on upstream endwall film cooling at leading edge of gas turbine blades[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(3): 191-195, 226.

[17] 沈菁菁. 燃气轮机叶片气膜冷却数值模拟[D]. 上海:上海发电设备成套设计研究院, 2014.

[18] 骆剑霞. 涡轮叶片内冷结构对外部气膜冷却特性的影响研究[D]. 西安: 西北工业大学, 2014.