基于正弦余弦算法的汽轮机热耗率预测
牛培峰, 吴志良, 马云鹏, 史春见, 李进柏
(燕山大学 工业计算机控制工程河北省重点实验室, 河北秦皇岛 066004)
热耗率是指发电机组每产生1 kW·h电能所消耗的热量.现在通常把热耗率作为研究和衡量电厂热经济性的一个重要指标[1],很多电厂都需要对其进行实时监测,精确的汽轮机热耗率值对电厂安全、稳定、高效运行具有重要意义.
由于汽轮机热耗率与其影响因素之间存在着复杂的非线性关系,传统的建模方法无法建立精确的数学模型,导致模型所得的热耗率值产生偏差.目前一种可行的方法是采用回归算法计算热耗率,王雷等[2]提出了基于支持向量回归算法的汽轮机热耗率模型;王惠杰等[3]提出基于v类型支持向量机(v-SVM)的汽轮机热耗率回归预测模型;张文琴等[4]基于偏最小二乘算法进行热耗率回归分析,建立了汽轮机热耗率预测模型;刘超等[5]提出基于最小二乘支持向量机的热耗率反向建模方法.基于数据驱动建模的人工神经网络也是解决这一问题的有效方法,朱誉等[6]提出基于BP神经网络的汽轮机热耗率在线计算方法,所建模型具有较高的准确性和稳定性.然而,常规的神经网络存在迭代训练时间长、计算量大、训练速度慢、泛化能力较差且易陷入局部极小点等不足.为克服这些缺点,笔者提出了一种改进的正弦余弦算法(ASCA)和快速学习网(FLN)[7]的综合建模方法.
正弦余弦算法(SCA)是由Mirjalili[8]于2016年提出的一种基于正弦余弦函数的新型优化算法,该算法通过创建多个随机候选解,利用正弦余弦数学模型来求解最优化问题,能够探索不同的搜索空间,有效避免局部最优,具有模型简单、调整参数少和全局寻优能力强等优点.然而在处理复杂的优化问题上,SCA算法的收敛精度较低且收敛速度较慢,为了克服这些缺陷,笔者提出了ASCA算法,并利用ASCA算法、SCA算法、经典的人工蜂群算法(ABC)[9]和教与学优化算法(TLBO)[10]分别对单峰、多峰等8个基准测试函数进行了测试.由于FLN模型的性能过于依赖随机初始的输入权值和隐藏层阈值,故采用ASCA算法对FLN模型的参数进行优化,为验证该模型的准确性和有效性,将其与SCA算法、ABC算法和TLBO算法的FLN模型进行了对比研究.
1 快速学习网
FLN是在2013年提出的一种新型双并联前馈神经网络,与极端学习机[11]不同的是,其输出层不仅可以接收来自隐藏层神经元的信息,而且还可以直接从输入层接收相关信息[12].因此,FLN模型可以看成是一种隐藏层到输出层的非线性和输入层到输出层的线性组合模型,其结构见图1.
设有N个观测样本{(xi,yi)},i=1,2,…,N,其中xi=[xi1,xi2,…,xin]T∈Rn,表示第i个样本的n维输入向量,n为输入层节点层个数;yi=[yi1,yi2,…,yil]∈Rl,表示第i个样本的l维输出向量.令隐藏层神经元个数为m,隐藏层激励函数为g(x),则FLN的数学模型可表示为:
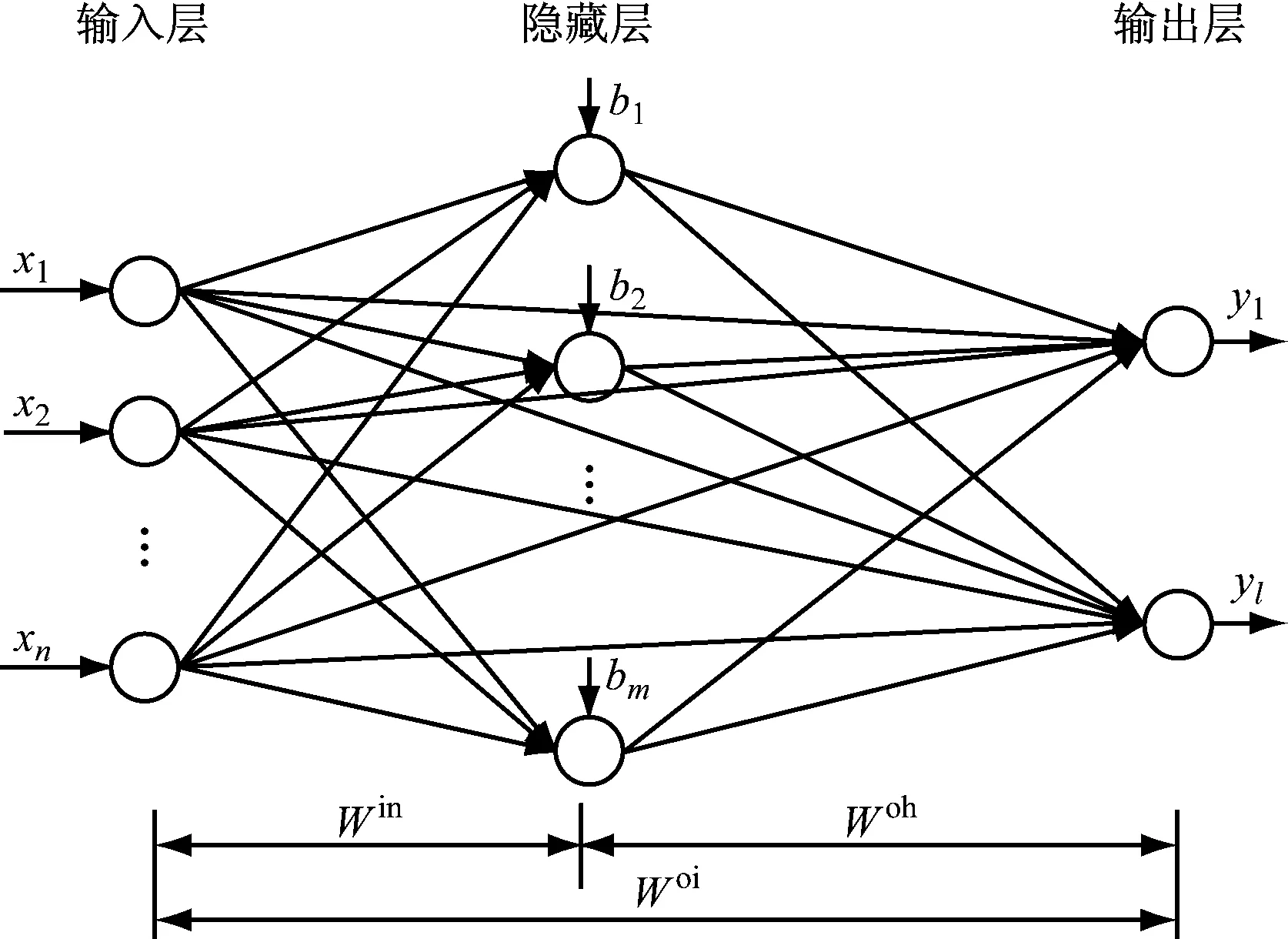
图1 快速学习网结构图
(1)
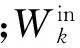
式(1)用矩阵形式可表示为:
(2)
(3)
(4)
式中:W为输出权值矩阵;G为隐藏层输出矩阵;Y为期望输出.
根据式(6),利用最小二乘范数解求法可得:
(5)
(6)
FLN算法步骤如下:(1) 随机生成输入权值矩阵Win和隐藏层阈值b;(2) 通过式(4)计算隐藏层输出矩阵G;(3) 通过式(5)计算输出权值矩阵W;(4)通过式(6)将输出权值矩阵W分为Woi和Woh.
2 正弦余弦算法
2.1 正弦余弦算法
SCA算法是基于正弦余弦数学模型进而提出的一种新型优化算法.一般来说,智能优化算法的初始点往往随机选取一系列个体,虽然无法保证在一次迭代过程中就能找到最优解,但如果有足够的个体和迭代次数,并利用目标函数进行反复评价,SCA算法可大大增加获得最优解的概率.
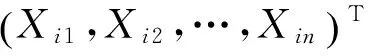
(7)

SCA算法中的4个主要参数为r1、r2、r3和r4.r1决定了下一个位置空间区域(或移动方向),此区域可以是候选解与目标解之间的任一区域或二者之外的区域.r2定义了靠近或远离目标位置时应该移动的步长.r3引进了一个随机权重,可以随机强调(r3>1)或减弱(r3<1)其对所定义距离的影响.r4表示何时选择式(7)中正弦或余弦数学模型进行位置更新.
2.2 改进的正弦余弦优化算法
与其他优化算法相比,SCA算法的优势在于模型简单、调节的参数少,仅仅利用正弦和余弦函数的性质进行迭代、寻找最优解,比较容易实现.但是SCA算法中的搜索完全依赖随机性,导致该算法收敛精度低、收敛速度慢.
针对SCA算法存在的上述缺陷,笔者提出了ASCA算法,该算法使得收敛速度和收敛精度得到了较大幅度的提升,改进点具体如下:
(1) 群体初始位置的Bloch坐标编码方案.
在量子计算中,最小的信息单位用量子位表示,量子位又称量子比特,一个量子比特的状态可表示为:
|φ>=cos (θ/2)|0>+eiφsin(θ/2)|1>
(8)
式中:φ和θ均为实数.
φ和θ定义了Bloch球面上一点P,见图2[13].
由图2可知,任何量子位都与Bloch球面上一点对应,因此量子位都可以用Bloch坐标表示:
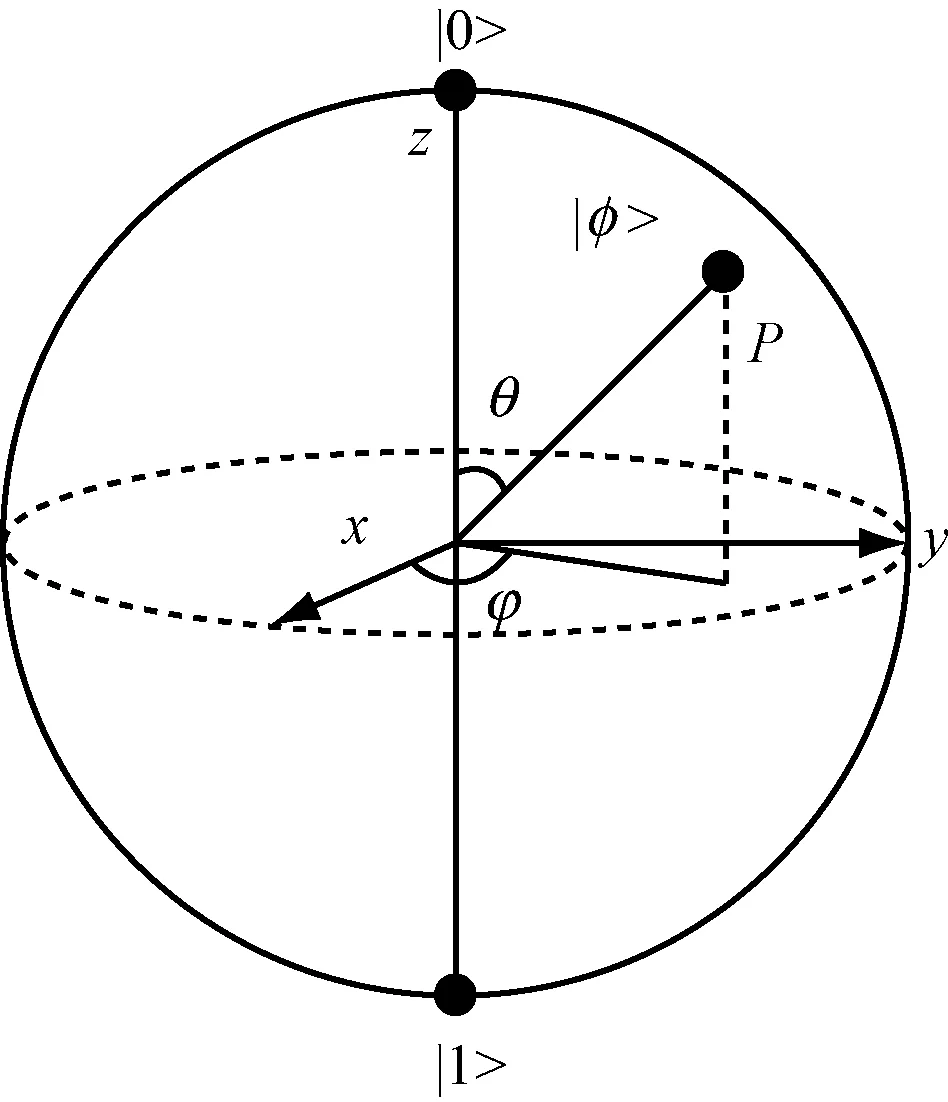
图2 量子比特的Bloch球面表示
(9)
直接采用量子位的Bloch坐标作为编码.设pi为群体中第i个候选解,其编码方案如下:
(10)
式中:φij=2π×r,θij=π×r,r为[0,1]区间的随机数;i=1,2,…,N;j=1,2,…,n;N为群体规模;n为优化空间的维数.
每个候选解同时占据空间的3个位置,即同时代表以下3个优化解,分别为X解、Y解和Z解.
Pix=(cosφi1sinθi1,…,cosφinsinθin)
(11)
Piy=(sinφi1sinθi1,…,sinφinsinθin)
(12)
Piz=(cosθi1,cosθi2,…,cosθin)
(13)
(14)
(15)
(16)
因此,每个候选解对应优化问题的3个解.在所有的候选解中选择N个适应度值较小的个体作为初始群体.
此种编码方式能扩展搜索空间的遍历性,增加群体的多样性,进而改善群体的质量,加快算法收敛速度.
(2) 在SCA算法中,为了增强局部开发能力,提高算法的收敛精度和收敛速度,引入惯性权重w对算法进行改进,加入的惯性权重为:
(17)
式中:w′和w″分别为惯性权重的最大值和最小值.
w随着迭代次数的增加而递减,使得迭代前期有利于全局探索,迭代后期有利于局部寻优,由于引进的w减小的幅度较大,更有利于算法进行局部开发,提高算法的收敛精度和收敛速度.
改进后的位置更新公式如下:

(18)
ASCA算法流程如下:①初始化算法参数,包括群体规模N、最大迭代次数Tmax、惯性权重的最大值w′和最小值w″;② 初始化群体位置,采用量子位Bloch球面对每个候选解进行编码,最后映射到优化问题的解空间,然后计算群体中每个个体的适应度值,根据适应度值的大小进行排序,最后选取N个适应度值较小的个体作为初始群体;③ 计算N个个体的适应度值,选择适应度值最小的个体位置作为最优位置;④根据r4值的大小,选择式(18)中的正弦或余弦数学模型来更新下一代的位置;⑤若达到最大迭代次数,则算法结束,输出最优个体,即算法找到的最优解,否则返回③.
3 ASCA算法性能测试
为了测试ASCA算法的性能,将其应用到5个基准优化问题(见表1)上,其中f1~f3为高维的单峰基准测试函数,f4和f5为高维的多峰基准测试函数.

表1 5个基准测试函数
为了说明ASCA算法的有效性,将其与SCA算法、ABC算法和TLBO算法进行比较.ABC算法中的参数“limit”设置为200,SCA算法和ASCA算法中的参数a设置为2,经过大量的仿真实验后,确定ASCA算法中惯性权重的最大值和最小值分别为w′=0.08,w″=0.01.
为了保证公平性,4种算法的相关参数设置相同:初始群体规模为40,迭代次数为1 000,实验独立运行次数为20.另外,对表1中的高维单峰和多峰基准测试函数的维数均设置为10、30和50 3种.以表格的形式记录各算法寻优的平均值(Mean)和均方差(SD),如表2所示.
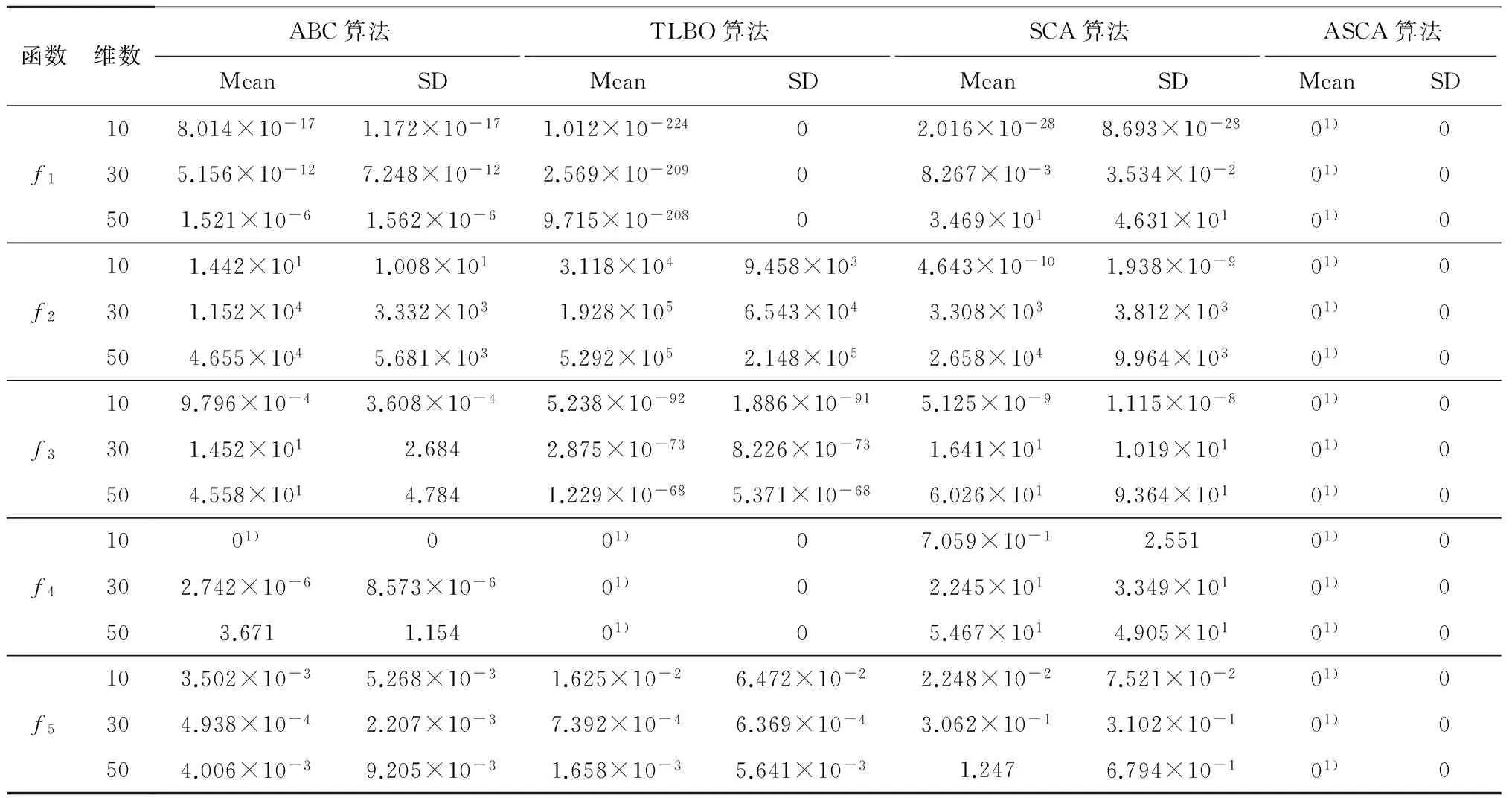
表2 4种算法对基准测试函数的运行结果
注:1) 表示最好的结果.
由表2可以看出,在设定的参数条件下,ASCA算法较SCA算法在精度上均有极大的提高, ASCA算法能够找到5种基准测试函数的理论最优值,并且随着维数的增加,ASCA比其他3种算法更稳定,搜索的精度依然很高;TLBO算法对f1和f32种基准测试函数的搜索精度非常高,但没有达到理论最优值,而ASCA算法能够找到理论最优值;另外对于f4来说,SCA算法找到的最优解精度很低,ABC算法只有在10维时才能找到理论最优值,而ASCA算法和TLBO算法在10、30和50维时都能找到理论最优值.由此可见,对于绝大部分的基准测试函数来说,与其他3种算法相比, ASCA算法找到的最优解不仅精度更高,而且其收敛速度也更快.总体来说,ASCA算法是一个非常高效的优化算法,可用于汽轮机热耗率预测模型的参数优化.
4 汽轮机热耗率建模
4.1 模型建立及参数优化
在汽轮机组运行过程中影响热耗率的因素很多,因此在建模前首先应对汽轮机相关的热力参数进行详细的物理分析,根据热耗率与输入参数之间的关联强度决定输入参数,应尽可能选择与热耗率直接发生联系的强关联参数,对于间接影响的参数,在可能的情况下应少选或者不选,这样可以提高热耗率预测模型的计算精度和建模速度.根据这个原则,并结合文献[14]和文献[15],最终选择发电负荷(Ne)、主蒸汽压力(p0)、主蒸汽温度(T0)、再热器出口蒸汽压力(pr)、再热器出口蒸汽温度(Tr)、再热器入口蒸汽压力(ph)、再热器入口蒸汽温度(Th)、再热减温水质量流量(qm,z)、过热减温水质量流量(qm,gl)、汽轮机背压(pb)、循环水入口温度(Tc)和给水质量流量(qm,fw)共12个参数作为模型输入变量,热耗率(Hr)作为输出变量,其计算见文献[16].
以某600 MW超临界汽轮机组为研究对象,从集散控制系统(DCS)数据库中随机采集12 d正常供热运行数据,其中春、夏、秋、冬四季各采集3 d,每隔2 h采集一次,每天12组,总共采集了144组多工况运行数据,基本覆盖了机组全天变负荷运行的典型工况,具体数据样本见表3.

表3 某600 MW超临界汽轮机组运行数据
对于FLN中随机初始化的输入权值和隐藏层阈值,很难确保得到的FLN模型具有较高的预测精度和较好的泛化能力.针对上述不足,利用ASCA算法对FLN模型的输入权值和隐藏层阈值进行优化,以目标函数适应度值最小为原则,通过判断是否达到最大迭代次数为循环终止条件,当循环结束后,将最优模型结构参数作为输入权值和隐藏层阈值代入FLN模型,即完成ASCA-FLN模型的建立.
ASCA算法的参数设置与前面相同,FLN模型的参数设置如下:隐藏层节点为20,隐藏层激励函数为“sigmoid”,输入权值和隐藏层阈值的寻优范围均为[-1,1],最大迭代次数为200.
在ASCA-FLN模型结构参数优化中,目标函数定义为:
(19)
式中:Yi为ASCA-FLN模型的热耗率预测值;y为热耗率实际值.
4.2 仿真结果及分析
同理,可建立ABC-FLN、TLBO-FLN和SCA-FLN模型.在FLN、ABC-FLN、TLBO-FLN、SCA-FLN和ASCA-FLN 5种预测模型中,随机选择120组测试数据作为训练样本,剩下的24组测试数据作为预测样本,用于验证所建模型的预测精度和泛化能力.5种预测模型参数设置为:群体规模为40,最大迭代次数为200,在ABC算法中参数“limit”设置为50,其他参数与上面仿真实验保持一致.仿真结果如图3和图4所示.
由图3可以看出,除个别组数据外,ASCA-FLN模型对训练样本都能进行很好地拟合,拟合度很高.由图4可以看出,ASCA-FLN模型能够对测试样本进行很好地预测,与FLN、ABC-FLN、TLBO-FLN和SCA-FLN模型相比,其预测精度要高很多,具有较强的泛化能力.
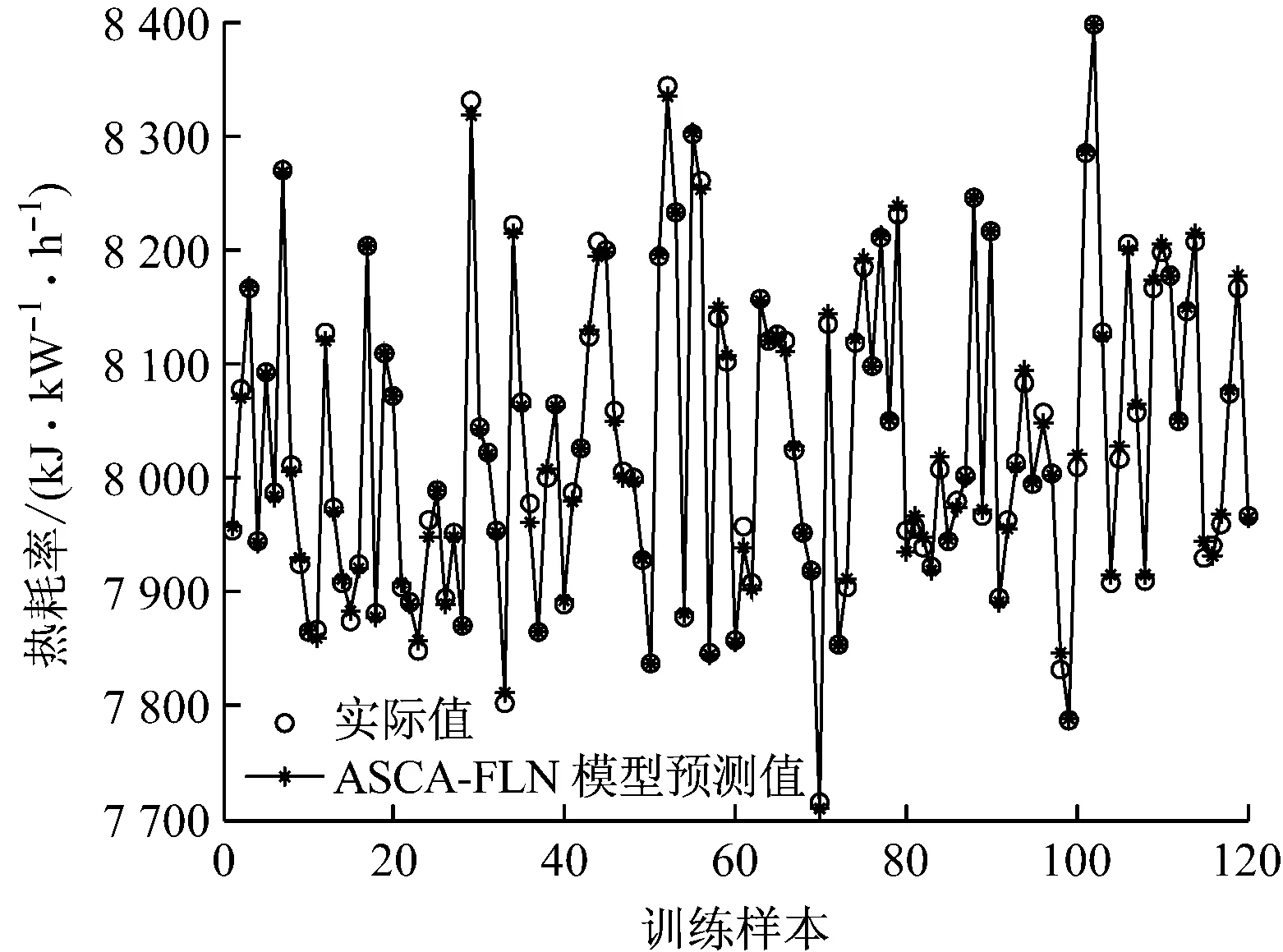
图3 训练样本预测值与实际值的对比
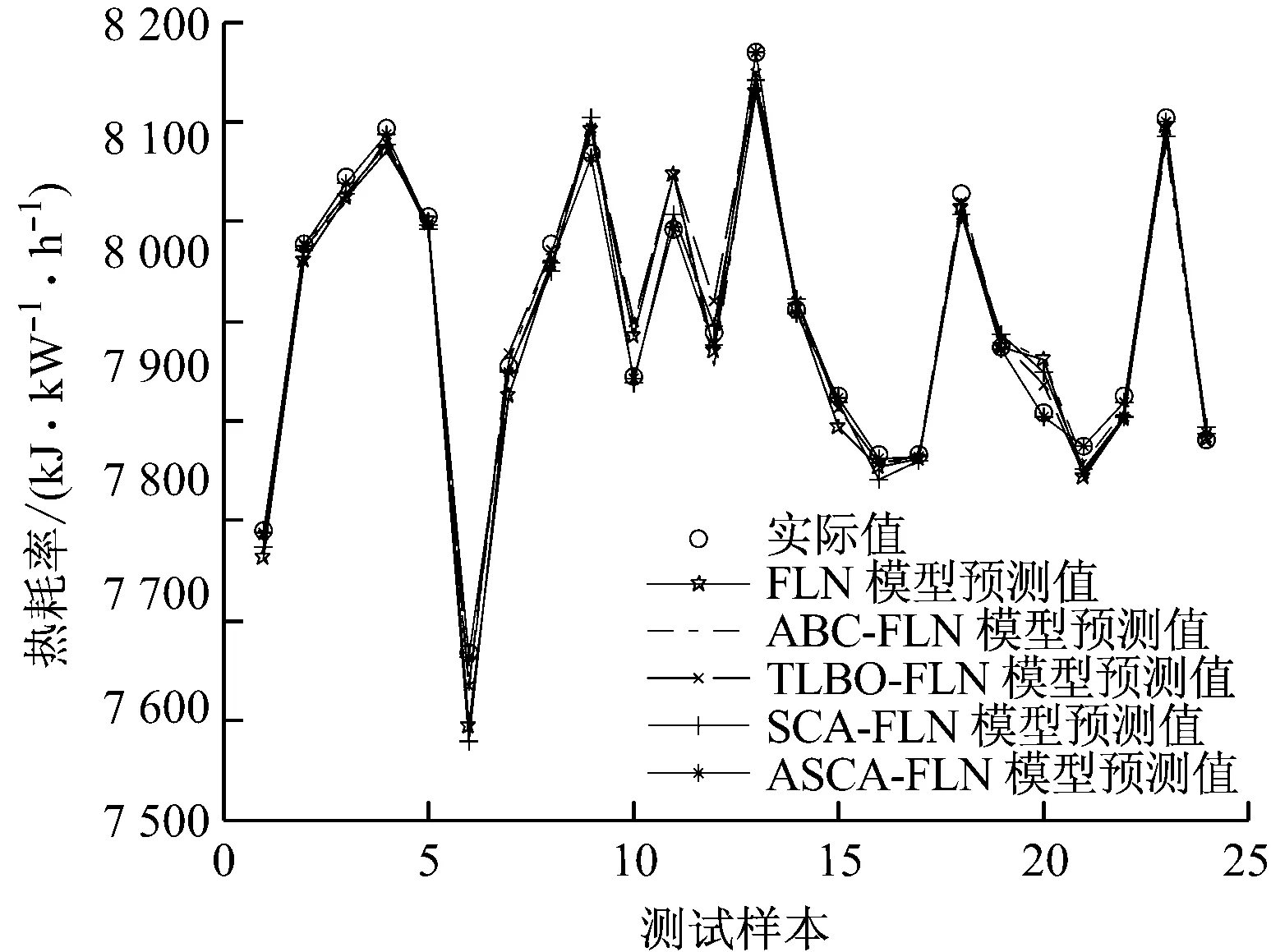
图4 测试样本预测值与实际值的对比
为了能更好地体现ASCA-FLN模型的预测效果,采取以下3个性能指标来综合评价5种预测模型的预测效果.
(1) 均方根误差(eRMSE).
(20)
(2) 平均相对百分比误差(eMAPE).
(21)
(3) 平均绝对误差(eMAE).
(22)
式中:y′为热耗率预测值.
各模型的输入变量、输出变量和样本数据均与ASCA-FLN模型相同,各算法的参数设置与前面一致,预测结果如表4和表5所示.

表4 训练样本准确度对比

表5 测试样本准确度对比
由表4可知,对于训练样本,与其他4种预测模型相比,ASCA-FLN模型的3种误差性能指标低很多,其中eRMSE为6.134,eMAPE为4.842×10-9,eMAE为4.756,其数值均远小于其他4种预测模型.因此,对于训练样本而言,ASCA-FLN模型具有较高的拟合精度.
由表5可知,对于测试样本,ASCA-FLN模型的eRMSE为6.745,eMAPE为1.351×10-5,eMAE为5.388,其数值均远小于其他4种预测模型,与FLN模型相比,效果更加突出.因此,对于测试样本而言,ASCA-FLN模型具有较强的泛化能力和较高的预测精度.
5种预测模型对测试样本的预测误差曲线如图5所示.由图5可以看出,ASCA-FLN模型的预测误差比较平稳,最大误差为20.206 kJ/(kW·h),与其他4种预测模型相比,ASCA-FLN模型的预测误差明显更小,说明该模型能够更精确地预测汽轮机的热耗率.
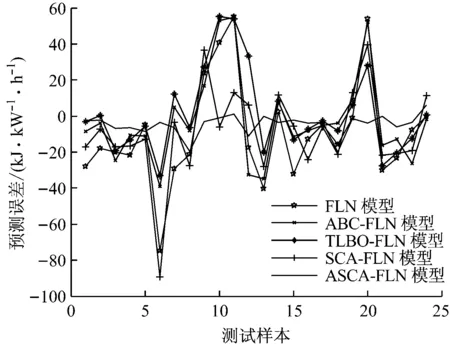
图5 各预测模型对测试样本的预测误差曲线
综上所述,建立的ASCA-FLN模型具有较强的泛化能力和较高的预测精度,非常适用于工程中汽轮机热耗率的预测.
5 结 论
以某火电厂600 MW超临界汽轮机组为研究对象,利用基于量子位Bloch坐标编码自适应的改进后正弦余弦算法优化快速学习网的模型参数,建立了ASCA-FLN模型.并将该模型对汽轮机热耗率的预测结果与FLN、ABC-FLN、TLBO-FLN和SCA-FLN模型的预测结果进行对比.结果表明,ASCA-FLN模型的预测精度更高,泛化能力更强,为火电厂汽轮机热耗率预测提供了一种新的方法.
[1] 郑体宽. 热力发电厂[M]. 2版. 北京: 中国电力出版社, 2008.
[2] 王雷, 张欣刚, 王洪跃, 等. 基于支持向量回归算法的汽轮机热耗率模型[J].动力工程, 2007, 27(1): 19-23, 49.
WANG Lei, ZHANG Xingang, WANG Hongyue, et al. Model for the turbine heat rate based on the support vector regression[J].JournalofPowerEngineering, 2007, 27(1): 19-23, 49.
[3] 王惠杰, 陈林霄, 李洋, 等. 基于v-SVM的汽轮机热耗率回归模型研究[J].动力工程学报, 2014, 34(8): 606-611, 645.
WANG Huijie, CHEN Linxiao, LI Yang, et al. Study on heat rate regression model of steam turbines based on v-SVM[J].JournalofChineseSocietyofPowerEngineering, 2014, 34(8): 606-611, 645.
[4] 张文琴, 付忠广, 靳涛, 等. 基于偏最小二乘算法的热耗率回归分析[J].现代电力, 2009, 26(5): 56-59.
ZHANG Wenqin, FU Zhongguang, JIN Tao, et al. Heat rate regression analysis based on partial least squares algorithm[J].ModernElectricPower, 2009, 26(5): 56-59.
[5] 刘超, 牛培峰, 游霞. 反向建模方法在汽轮机热耗率建模中的应用[J].动力工程学报, 2014, 34(11): 867-872, 902.
LIU Chao, NIU Peifeng, YOU Xia. Application of reversed modeling method in prediction of steam turbine heat rate[J].JournalofChineseSocietyofPowerEngineering, 2014, 34(11): 867-872, 902.
[6] 朱誉, 冯利法, 徐治皋. 基于BP神经网络的热经济性在线计算模型[J].热力发电, 2008, 37(12): 17-19, 30.
ZHU Yu, FENG Lifa, XU Zhigao. An on-line calculation model of thermal economic efficiency based BP neural network[J].ThermalPowerGeneration, 2008, 37(12): 17-19, 30.
[7] LI Guoqiang, NIU Peifeng, DUAN Xiaolong, et al. Fast learning network: a novel artificial neural network with a fast learning speed[J].NeuralComputingandApplications, 2014, 24(7/8): 1683-1695.
[8] MIRJALILI S. SCA: a sine cosine algorithm for solving optimization problems[J].Knowledge-BasedSystems, 2016, 96: 120-133.
[9] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. [S.l.]:Technical Report-TR06, 2005.
[10] RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems[J].Computer-AidedDesign, 2011, 43(3): 303-315.
[11] HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: theory and applications[J].Neurocomputing, 2006, 70(1/3): 489-501.
[12] 李国强. 新型人工智能技术研究及其在锅炉燃烧优化中的应用[D]. 秦皇岛: 燕山大学, 2013.
[13] 李士勇, 李盼池. 量子计算与量子优化算法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2009.
[14] 吕太, 吴海波, 胡乔良. 汽轮机最佳运行工况的经济性试验分析[J].东北电力大学学报, 2010, 30(1): 1-4.
LÜ Tai, WU Haibo, HU Qiaoliang. Experimental study about optimal operating conditions of the steam turbine[J].JournalofNortheastDianliUniversity, 2010, 30(1): 1-4.
[15] 云曦, 阎维平. 火电厂汽轮机组影响热耗率计算的因素[J].东北电力技术, 2007, 28(3): 15-18.
YUN Xi, YAN Weiping. Factors effecting heat consumption calculation for steamed turbine of fossil-fired power plant[J].NortheastElectricPowerTechnology, 2007, 28(3): 15-18.
[16] 盛德仁, 李蔚, 陈坚红, 等. 汽轮机组热耗率分析及实时计算[J].热力发电, 2003, 32(5): 16-18.
SHENG Deren, LI Wei, CHEN Jianhong, et al. Analysis and real-time calculation of specific heat consumption for steam turbine unit[J].ThermalPowerGeneration, 2003, 32(5): 16-18.

