引入曲面变分实现点云法矢一致性调整
何 华,李宗春,闫荣鑫,杨再华,阮焕立,付永健
1. 信息工程大学地理空间信息学院,河南 郑州 450001; 2. 北京卫星环境工程研究所,北京 100094
点云法矢作为点云数据的一项基本几何属性,在点云数据配准[1]、分割[2-3]和重建[4]中发挥着重要作用。点云法矢计算可以分为法矢估算和法矢一致性调整两个步骤。目前,法矢估算方法计算出的点云法矢指向不一致(一部分指向曲面外侧,另一部分指向曲面内侧),无法直接应用于后续的配准、分割和重建等处理步骤,故对点云的法矢进行一致性调整极为必要。
从单个测站获取的点云,依据点云与测站的相互位置关系,法矢一致性调整易于实现[5]。但是从多个测站获取的点云,其法矢一致性调整的复杂性和困难性骤增。目前,法矢一致性调整方法主要包括最小生成树法(minimum spaning tree,MST)[6-15]、光度立体视觉法[16]和曲面重建法[3,17-19]。光度立体视觉法依据曲面反射与光照几何等先验信息来计算曲面法矢,算法稳定性差,对于低质量的点云很难得到完全一致的法矢调整结果。曲面重建法用重采样后原始点云的均匀分布近似结构(如粒子系统和三角网格)的法矢调整点云法矢,处理流程复杂,时间消耗太大。最小生成树法稳健性好,原理简单且易于实现,是目前应用最为广泛的法矢调整算法,故本文对最小生成树类算法展开深入研究。文献[6]首先提出了基于最小生成树的法矢一致性调整算法。该算法调整一个法矢需遍历全部点云,效率较低。当点云数据量大时,算法几无应用价值。文献[7—8]采用法向距离区分平缓点和非平缓点,并通过判断采样点的k-邻域点内是否存在非平缓点而采取不同的法矢调整方式,法矢调整效率有所提高,但法向距离不具有几何不变性,其阈值设定比较困难,因此算法适用范围有限。文献[9—10]通过缩小传播法矢搜索范围来提高法矢调整的效率,但是在高曲率区域,法矢传播容易出错。文献[11—12]通过缩小搜索范围、增加每次法矢传播个数等策略改进了MST算法,同时该算法考虑了奇异情况下的点云法矢调整,但算法的效率有待提高。文献[13]着重研究了点云模型有相邻曲面的法矢调整,但是需要进行两遍法矢一致性调整,算法效率低。
针对单目标对象的点云数据,现有的法矢一致性调整算法能够调整法矢指向同一侧,但是算法的准确度和效率均需进一步提高。曲面变分[20]反映了采样点局部区域的平缓程度,具有几何不变性,可作为判断采样点是否为平缓点的依据,进而益于针对平缓点和非平缓点采用相应的法矢调整策略,提高法矢调整效率。基于此,本文提出一种基于曲面变分的点云法矢一致性调整方法,来提高单目标对象点云法矢一致性调整的准确性和效率。
1 点云法矢和曲面变分估算
1.1 点云法矢估算
点云中的任意一点Pi所在的局部区域可近似为平面,点Pi的法矢ni可以用该点的k-邻域点基于最小二乘法拟合得到的局部平面法向量来逼近,即
(1)
式中,n为平面H的法向量;D为坐标原点到平面H的距离。
式(1)可以转换为PCA。PCA的协方差矩阵C根据点Pi的邻域点构建,对于任意点Pi,其对应的协方差矩阵为
(2)
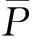
设矩阵C的3个特征根为λ0、λ1、λ2,对应的特征向量为e0、e1、e2,且λ0≤λ1≤λ2,则最小特征根λ0对应的特征向量e0即为点Pi的法矢ni。为便于后续运算,对所有法矢予以单位化处理。
1.2 点云曲面变分估算
点Pi的协方差矩阵C的特征向量e0、e1、e2构成一个正交坐标系,其中e1和e2构成了点Pi处的切平面,e0近似为曲面在点Pi处的法矢。特征根λ0、λ1、λ2表征了点Pi沿着对应的特征向量e0、e1、e2的偏移量,即λ0定量表示了点Pi偏离其切平面的程度。故类比于微分几何学中用曲率来描述曲面的微分性质,可以将曲面变分[19]作为散乱点云局部曲面微分性质的衡量准则。点Pi局部区域的曲面变分定义为
(3)
式中,σ(Pi)表征了点Pi所在局部区域的平缓程度;σ(Pi)越小表示点Pi所在局部区域越平缓。由于λ0为最小特征根,故σ(Pi)的取值范围为0≤σ(Pi)≤1/3。当σ(Pi)等于1/3时,表示点Pi是一个非平缓点,其邻域点所在区域为高曲率区域;当σ(Pi)等于0时,表示点Pi的邻域点分布在平面上,点Pi是一个平缓点。故可以利用σ(Pi)来度量点Pi是否为平缓点,如设置阈值σ0,当σ(Pi)小于σ0时为平缓点,否则为非平缓点。
曲面变分作为描述曲面局部几何特征的指标,与曲面曲率具有相似性,广泛应用于点云数据简化等领域。同时,曲面变分具有几何不变性,其大小和点云模型的尺度无关,与法向距离相比,用曲面变分来区分平缓点和非平缓点适用性更强,且阈值σ0可以根据下文设置的规则自动获取,无须过度依赖个人经验。
研究表明,植物中大多数MYB蛋白具有2个重复的MYB结构域(R2R3)。本研究经过序列比对发现,LhsorMYB12基因序列中存在R2、R3结构域,与其他物种的MYB转录因子结构域具有高度同源性(图3)。另外, R3结构域中还存在MYB和bHLH蛋白相互作用的特异性标签基序[24]。基因结构分析表明,LhsorMYB12由3个外显子和2个内含子组成,与拟南芥、苜蓿(Medicago truncatula Gaertn.)、葡萄(Vitis vinifera L.)的MYB基因结构类似(图4)。
2 法矢一致性调整
通过PCA计算出的点云法矢,一部分指向曲面内侧,另一部分指向曲面外侧,若不对其进行一致性调整,会极大地限制后续的点云数据处理。鉴于现有法矢一致性调整算法的稳健性差、效率低的情况,本文从提高法矢调整准确性和效率两方面来设计算法。
2.1 算法原理
为提高法矢一致性调整的准确性,当法矢传播起点与法矢待传播点有且只有一个是平缓点时,以两点的法矢ni、nj与两点连线的方向向量mij的夹角来约束点云法矢传播方向。为提高法矢一致性调整的效率,本算法用σ(Pi)来区分平缓点和非平缓点,并采取相应的法矢调整策略,且本算法把待传播法矢的搜索范围从所有点云缩小到点的k-邻域范围。在k-邻域范围内,只要待传播法矢满足相关条件,即调整该法矢方向,这样可以增加每次邻域搜索时法矢传播的个数。法矢一致性调整的流程如图1所示。
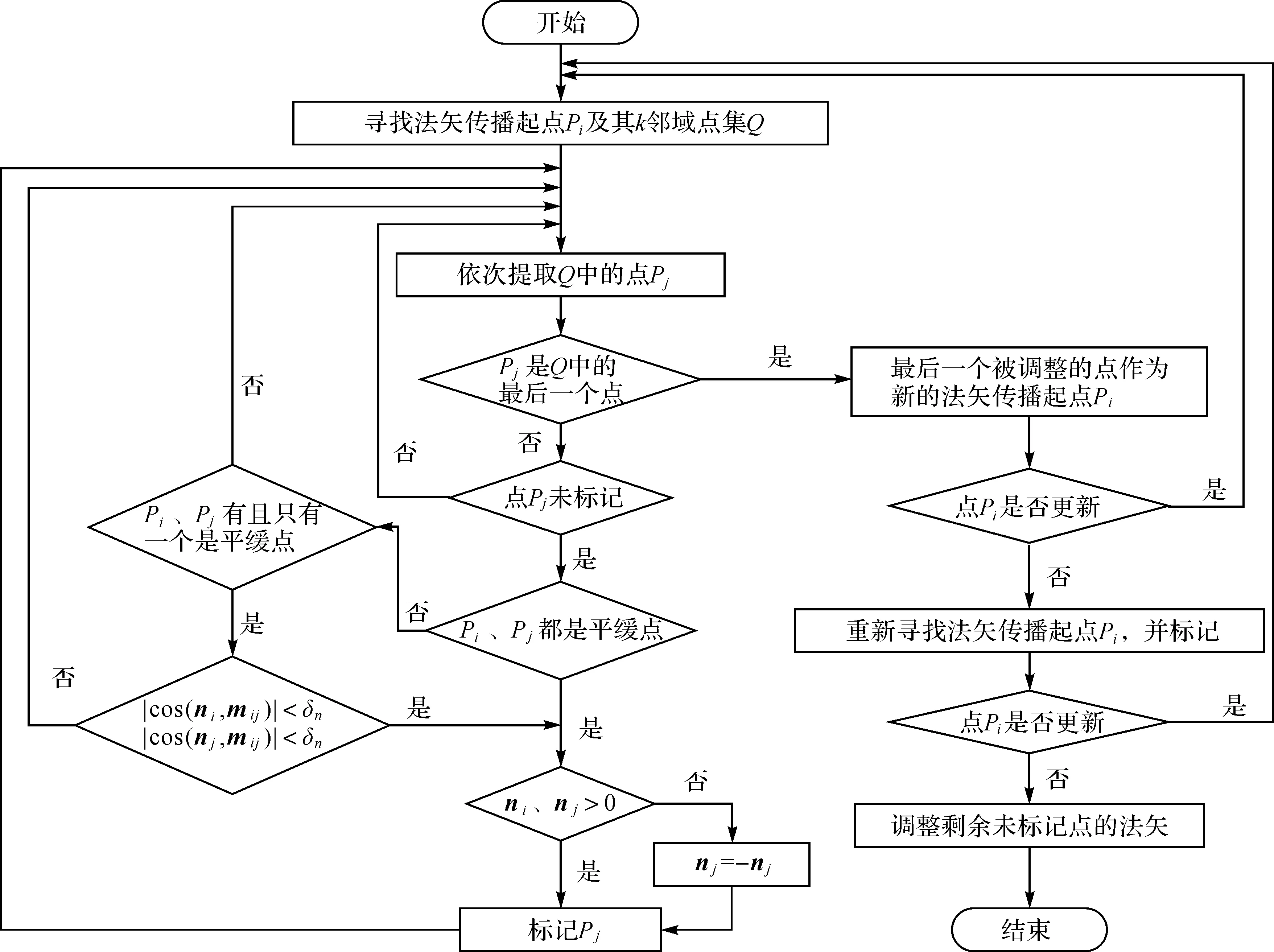
图1 法矢调整流程图Fig.1 Flow chart of adjusting normal vector
从图1可知,法矢一致性调整时首先需要寻找法矢传播起点,本文使用的寻找方法为:第1次寻找法矢传播起点Pi时,按照下标i最小原则,寻找一个平缓点作为法矢一致性调整的起点;重新寻找法矢传播的起点时,按照下标最小原则,在未标记的点中寻找一个平缓点,并用该点邻域中距离该点最近的已标记平缓点法矢调整该点法矢,把该点作为新的法矢调整起点。之所以采用平缓点作为法矢传播起点,是因为法矢传播从平缓区域开始有利于减少算法耗时。调整剩余未标记点的法矢时,用距离未标记点最近的已标记点调整该点的法矢。本算法中,待传播法矢的搜索范围仅在点的邻域内,搜索范围大幅度减小,且每次在邻域范围内传播法矢时,法矢传播个数不止一个。
2.2 参数确定
在法矢一致性调整过程中,需要确定k-邻域中参数k、曲面变分阈值σ0和两向量夹角余弦绝对值阈值δn的数值,3个参数的取值会影响法矢调整结果和效率,下面具体讨论参数的取值策略。
参数k对点云法矢调整影响较大。在点云的稀疏或高曲率区域,若取值偏大,此时局部区域内的k邻域点的法矢指向不能严格地保持一致,可能导致错误的法矢调整结果,故k的取值要小一些。在点云的密集或平缓区域,局部区域内的k邻域点的点云法矢指向一致,此时适当增大k的取值有利于提高算法的效率。根据多次试验测试,k取值范围在15至35之间时能够适应绝大多数类型的点云数据情况,本文k值取为25。
一般而言,平缓点占点云数据的绝大部分,而非平缓点只占点云数据中很少的一部分。假设点云中的非平缓点占所有点云的比值记为符号q且所有点按照其曲面变分值升序排列,则阈值σ0为
(4)
式中,int表示取整函数;n为点云数量。为了不遗漏非平缓点同时兼顾法矢一致性调整的效率,本文q取值为10%。
文献[25]证明了法矢传播方向应该是沿着法矢的切线方向而不是法矢方向。故由点Pi指向Pj的单位向量mij与点Pi的法矢之间的夹角θ应该接近90°,此时点Pj的法矢才能根据点Pi的法矢进行调整,否则不调整点Pj的法矢。考虑到点云局部曲面的变化,θ合适的取值范围为60°<θ<120°,因此两向量夹角余弦值的绝对值应该小于0.5,即阈值δn取值为0.5。
虽然人为设置的阈值存在一定的不确定性,但是只要阈值在合理范围内,均可得到正确的法矢调整结果。3个参数按照上述的取值方法一般可以获得较好的法矢调整结果。对于薄壁等奇异区域的点云数据,需要参考上述的参数取值策略来调整参数的取值,以期获得良好的法矢一致性调整结果。
3 试验结果与分析
为测试本文算法效果,在Windows 7系统Intel(R) Core(TM) i7-4790M CPU 3.60 GHz硬件环境下,利用VS2010和点云库(point clouds library,PCL)分别实现了文献[9]算法、文献[11]算法和本文算法,并对法矢一致性调整结果进行可视化显示,为了更加直观地观察法矢调整结果,使所有法矢尽可能指向物体内侧。hand、block和mannequin的法矢调整结果如图2所示。

图2 法矢一致性调整结果Fig.2 Results of consistent normal vector adjustment
从图2(a)可知,PCA计算出的法矢指向不一致,需要进行一致化处理。从图2(b)可知,文献[9]算法在点云的平缓区域能得到正确的法矢调整结果,对于尖锐特征或高曲率区域的点云法矢,如hand的手指区域、block的直角棱边区域和mannequin的耳朵等区域,法矢变化比较剧烈,法矢调整容易出现错误。从图2(c)可知,文献[11]算法以MST算法为基础,可得到正确的法矢调整结果。从图2(d)可知,由于本文算法增加了法矢传播方向的约束条件,故在特征区域及平缓区域的法矢均得到了正确调整。
为比较算法效率,分别统计文献[9]算法、文献[11]算法和本文算法的法矢调整耗时,结果如表1所示。
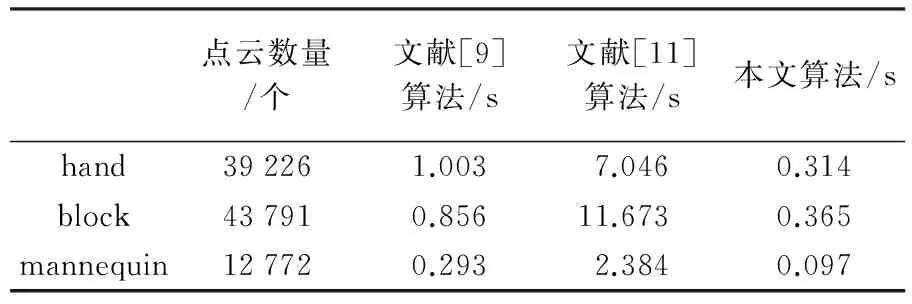
表1 法矢一致性调整耗时统计
从表1可知,文献[11]算法耗时最多,文献[9]算法次之,本文算法耗时最少。本文算法耗时与点云数据量成正比关系,与文献[9]算法相比,本文算法效率提高了大约2倍,与文献[11]算法相比,本文算法效率提高了数十倍。文献[11]算法的搜索范围比文献[9]算法及本文算法的搜索范围大,需要在已调整点和未调整点的交界区域进行遍历,故算法耗时最多。文献[9]算法和本文算法的搜索范围相当,但是文献[9]算法不区分平缓点与非平缓点,对所有点采取相同法矢调整策略,故其算法耗时多于本文算法。本文算法引入曲面变分来区分平缓点和非平缓点,根据已调整点和待调整点的类型采用不同的法矢调整策略,大大缩短了法矢调整的时间。同时本文算法法矢传播搜索范围小,且每次邻域搜索时,可传播多个法矢,算法耗时进一步减少。
4 结 论
本文提出了一种基于曲面变分的法矢一致性调整算法,通过区分平缓点和非平缓点、缩小传播法矢搜索范围、增加每次邻域搜索时法矢传播的个数、增加法矢传播方向约束等策略来提高法矢调整的准确性与效率。试验结果表明,本文算法能够获取正确的法矢一致性调整结果,且算法效率高于文献[9]和文献[11]算法。在薄壁、相离曲面、稀疏高曲率等奇异区域,点云k邻域点的法矢可能出现指向不一致的情况,致使本文算法的法矢一致性调整结果有可能出现错误,故下一步将重点研究本文算法在这三类奇异区域的稳健性以及k值的自适应选取问题。
[1] 陶海跻, 达飞鹏. 一种基于法向量的点云自动配准方法[J]. 中国激光, 2013, 40(8): 179-184.
TAO Haiji, DA Feipeng. Automatic Registration Algorithm for the Point Clouds Based on the Normal Vector[J]. Chinese Journal of Lasers, 2013, 40(8): 179-184.
[2] 董震, 杨必胜. 车载激光扫描数据中多类目标的层次化提取方法[J]. 测绘学报, 2015, 44(9): 980-987. DOI: 10.11947/j.AGCS.2015.20140339.
DONG Zhen, YANG Bisheng. Hierarchical Extraction of Multiple Objects from Mobile Laser Scanning Data[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 980-987. DOI: 10.11947/j.AGCS.2015.20140339.
[3] 张强, 李朝奎, 李俊晓, 等. 一种改进的基于法矢方向调整的平面点云分割方法[J]. 地理与地理信息科学, 2015, 31(1): 45-48.
ZHANG Qiang, LI Chaokui, LI Junxiao, et al. Planar Point Cloud Segmentation Based on the Weighted Average of Adjusted Normal Vector[J]. Geography and Geo-Information Science, 2015, 31(1): 45-48.
[4] 方悄云, 吕东辉, 孙九爱. 改进的物体表面重建的三角网格法[J]. 应用科学学报, 2016, 34(2): 145-153.
FANG Qiaoyun, LV Donghui, SUN Jiuai. Improved Triangle Mesh Method for Surface Reconstruction from Normal Field[J]. Journal of Applied Sciences, 2016, 34(2): 145-153.
[5] 朱德海, 郭浩, 苏伟. 点云库PCL学习教程[M]. 北京: 北京航空航天大学出版社, 2012.
ZHU Dehai, GUO Hao, SU Wei. The Learning Tutorial for Point Cloud Library PCL[M]. Beijing: Beihang University Press, 2012.
[6] HOPPE H, DEROSE T, DUCHAMP T, et al. Surface Reconstruction from Unorganized Points[J]. ACM SIGGRAPH Computer Graphics, 1992, 26(2): 71-78.
[7] 贺美芳. 基于散乱点云数据的曲面重建关键技术研究[D]. 南京: 南京航空航天大学, 2006.
HE Meifang. Research on Key Technologies of Surfaces Reconstruction Based on Scattered Point Cloud Data[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006.
[8] 肖天姿. 散乱点云的数据预处理及曲面重建研究[D]. 大连: 大连海事大学, 2012.
XIAO Tianzi. Research on Data Preprocessing and Surface Reconstruction of Scattered Point Cloud[D]. Dalian: Dalian Maritime University, 2012.
[9] 孟祥林, 何万涛, 赵灿, 等. 逆向工程中点云邻域搜索及法矢估算相关算法研究[J]. 制造技术与机床, 2009(2): 44-47.
MENG Xianglin, HE Wantao, ZHAO Can, et al. Point Cloud-nearest-neighbor Search and Normal Vector Estimation Relative Algorithm in Reverse Engineering[J]. Manufacturing Technology & Machine Tool, 2009(2): 44-47.
[10] 何学铭. 点云模型的孔洞修补技术研究[D]. 南京: 南京师范大学, 2013.
HE Xueming. Research on Hole Filling Technology of Point Cloud Model[D]. Nanjing: Nanjing Normal University, 2013.
[11] 孙金虎. 点云模型分割与融合关键技术研究[D]. 南京: 南京航空航天大学, 2013.
SUN Jinhu. Research on Key Technologies of Point Cloud Segmentation and Fusion[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013.
[12] 孙金虎, 周来水, 安鲁陵. 点云模型法矢调整优化算法[J]. 中国图象图形学报, 2013, 18(7): 844-851.
SUN Jinhu, ZHOU Laishui, AN Luling. Optimal Algorithm for Normal Adjustment of Point Clouds[J]. Journal of Image and Graphics, 2013, 18(7): 844-851.
[13] 易倩宇. 高质量鲁棒曲面重建[D]. 杭州: 浙江大学, 2014.
YI Qianyu. High-quality and Robust Surface Reconstruction[D]. Hangzhou: Zhejiang University, 2014.
[14] 张剑清, 李彩林, 郭宝云. 基于切平面投影的散乱数据点快速曲面重建算法[J]. 武汉大学学报(信息科学版), 2011, 36(7): 757-762.
ZHANG Jianqing, LI Cailin, GUO Baoyun. A Fast Surface Reconstruction Algorithm for Unorganized Points Based on Tangent Plane Projection[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 757-762.
[15] 刘健. 可修正的点云一致定向[D]. 大连: 大连理工大学, 2014.
LIU Jian. Mendable Consistent Orientation of Point Clouds[D]. Dalian: Dalian University of Technology, 2014.
[16] SUN Jiuai, SMITH M, SMITH L, et al. Examining the Uncertainty of the Recovered Surface Normal in Three Light Photometric Stereo[J]. Image and Vision Computing, 2007, 25(7): 1073-1079.
[17] LIU Shengjun, WANG C C L. Orienting Unorganized Points for Surface Reconstruction[J]. Computers & Graphics, 2010, 34(3): 209-218.
[18] 曾峰, 钟治初, 杨通, 等. 基于SOM的散乱点云法矢计算[J]. 计算机工程, 2012, 38(8): 287-290.
ZENG Feng, ZHONG Zhichu, YANG Tong, et al. Scattered Point Cloud Normal Vector Calculation Based on SOM[J]. Computer Engineering, 2012, 38(8): 287-290.
[19] MULLEN P, GOES F D, DESBRUN M, et al. Signing the Unsigned: Robust Surface Reconstruction from Raw Pointsets[J]. Computer Graphics Forum, 2010, 29(5): 1733-1741.
[20] PAULY M, GROSS M, KOBBELT L P. Efficient Simplification of Point-sampled Surfaces[C]∥Proceedings of the IEEE Visualization Conference. Boston, MA, USA: IEEE, 2002.
[21] PAULY M, KEISER R, KOBBELT L P, et al. Shape Modeling with Point-sampled Geometry[J]. ACM Transactions on Graphics (TOG), 2003, 22(3): 641-650.
[22] LEVIN D. The Approximation Power of Moving Least-squares[J]. Mathematics of Computation, 1998, 67(224): 1517-1531.
[23] AMENTA N, BERN M. Surface Reconstruction by Voronoi Filtering[J]. Discrete & Computational Geometry, 1999, 22(4): 481-504.
[24] DEY T K, GOSWAMI S. Provable Surface Reconstruction from Noisy Samples[C]∥Proceedings of the 12th Annual Symposium on Computational Geometry. New York: ACM, 2004: 330-339.
[25] HUANG Hui, LI Dan, ZHANG Hao, et al. Consolidation of Unorganized Point Clouds for Surface Reconstruction[J]. ACM Transactions on Graphics, 2009, 28(5): 1-7.

