基于三维狄洛尼三角网的曲面重建算法

贾军辉，黄 明,3，刘祥磊

1. 北京建筑大学测绘与城市空间信息学院,北京 100044； 2. 北京市建筑遗产精细重构与健康监测重点实验室,北京 100044； 3. 代表性建筑与古建筑数据库教育部工程中心,北京 100044

三维激光扫描技术作为一种精确高效的测量手段，其应用领域不断拓展，对三维激光扫描的点云数据进行三维建模的需求逐渐增大。曲面重建技术作为三维建模的核心技术之一，在逆向工程、计算机视觉、计算机制图以及虚拟现实技术领域都有非常广泛的应用前景。

三维点云的曲面重建是基于点云完成对曲面的一种近似操作，文献[1]利用几何结构来表达三维图形，并由此引出曲面重建的方法。近年来，曲面重建越来越受到关注，并有很多理论和技术应用其中，比较经典的有变分法[2-3]、Level Set方法[4]、Alpha Shapes算法[5]、隐式曲面[6-7]、尺度空间模型[8]以及狄洛尼三角网[9]。目前应用最为广泛的是隐式曲面重建算法，如移动最小二乘算法[10]、Poisson曲面重建算法[11-13]、HRBF曲面重建算法[14]以及RIMLS法[15]。隐式曲面重建算法主要是通过局部、全局或者分段平整度指示函数来构建隐式曲面，然后利用Matching Cubes算法[16]或者Dual Contouring算法[17]提取等值面完成曲面重建。此外，文献[18]提出的Wrapping算法也类似于上述隐式曲面算法，但是它没有提取等值面，而是基于Morse理论对狄洛尼三角形复杂度的定义，对单形聚类进行溃减操作。基于尺度空间和多尺度分析的算法[19-20]重建效果较好，但是应用于大型曲面模型时重建效率较低，而且无法保证重建曲面正确的拓扑结构。文献[21—22]提出的Ball-Pivoting算法和Natural Neighbor Interpolation算法都属于曲面生长算法的范畴，重建曲面的速度较快，但是同样无法保证曲面的拓扑正确性，并且需要准确的参数设置才能重建出理想的效果。文献[23—24]提出的曲面重建算法采用了曲面生长的思想，在此基础上引入狄洛尼三角形的概念，以此克服传统曲面生长算法的缺点。但是这两种算法的程序本身计算三维狄洛尼三角网的效率较低，并且约束条件存在不足，从而严重制约了算法的广泛应用。

本文提出一种基于三维狄洛尼三角网的曲面重建算法。算法的思路是：在一定的约束条件下，按最优三角形选择标准，从预先构建好的三维狄洛尼三角网中逐个筛选出最优三角形添加到生长曲面上，最终输出的曲面是由一系列显式三角形组成的流形曲面。

1 算法原理

1.1 数据结构

曲面重建是一个不断选择符合约束条件的三角形，然后添加到重建曲面S上的过程。在曲面重建过程中，存在3种数据形式：采样点集P、重建曲面S以及曲面边界∂S，如图1所示。采样点(point)、边(edge)结构和三角形(triangle)结构是组成上述3种数据形式的基本数据单元。图2是算法所使用的三角形(triangle)结构。

图1 算法数据形式Fig.1 Algorithm data form

图2 三角形(Triangle)结构示意图Fig.2 Schematic diagram of triangle structure

结合图1、图2，T是在边界∂S上选出的最优三角形，与∂S存在一条公共边CE。CE的起点为P1，终点为P2，所对三角形顶点为Pn，Pn既可以是曲面S外的一点，也可以是边界∂S上的一点，但绝不可能是曲面S内的点。P1、P2在边界∂S上，P1所对三角形的边为E1，P2所对三角形的边为E2。这种数据结构便于构建曲面正确的拓扑关系，同时构建了不同拓扑元素的索引结构，在对三角形进行计算、添加、移除等操作时，必须按照这个结构进行，否则将无法保证重建曲面的正确性。

1.2 算法流程

本算法需要一个种子三角形作为起始条件，然后根据算法的约束条件来拓展曲面。算法首先利用点云数据构建三维狄洛尼三角网，它包含了曲面重建所需的所有三角面片，然后按照约束条件从三维狄洛尼三角网中提取正确的三角面片。此外，在重建点云数量在百万级以上的点云数据时，为防止程序占用内存过大，算法会先对点云数据进行分块，然后依次对各个分块点云进行重建，算法整体流程如图3所示。

图3 算法整体流程图Fig.3 The overall flow chart of the algorithm

1.2.1 三维狄洛尼三角剖分

对采样点进行三维狄洛尼三角剖分主要是为曲面提取阶段提供拓扑结构优良、网格质量较好的三维狄洛尼三角网。三维狄洛尼三角剖分也叫四面体剖分，因为扫描产生的采样点集是三维空间实体的某种映射，而空间实体的基本单形是四面体，即任何体都可以由多个四面体组成，所以采样点集的三维狄洛尼三角剖分的结果其实是四面体的集合。三维狄洛尼三角剖分在三维建模中具有重要的作用，但这是一件非常繁重并且耗时的任务，不过相关算法已经相当成熟，例如CGAL的3D Triangulation Data Structure模块[25]和TetGen三角剖分器[26]。考虑到程序本身的效率、模型的可操作性和数据使用的便利性，本文采用TetGen生成初始的三维狄洛尼三角网。

TetGen是一款优良的三维狄洛尼三角剖分器，它可以作为一个独立的程序使用。利用输入的三维点集，TetGen可以生成三维狄洛尼三角网(图4)，如果采样点集是经过加权的，即每个点都分配了一个实数作为它的权重，那么TetGen也可以生成采样点和三角网对应的权重图。本文只利用它生成三维狄洛尼三角网。

1.2.2 曲面提取

本算法本质上是一个贪心算法，即新的三角面片都需要在已构建曲面的基础上进行选择，那么这就需要一个起始条件来启动算法，然后按照特定的约束条件，从三维狄洛尼三角网(记为DT)中选择合适的三角面片进行添加，提取正确的曲面。

图4 TetGen 3D Delaunay三角剖分示意图Fig.4 Schematic diagram of TetGen 3D Delaunay triangulation

1.2.3 算法初始化

将三角形的外接圆半径记为半径参数rt，DT中rt最小的三角形设为种子三角形，作为算法的起始条件。将种子三角形加入曲面S中，这里曲面S即是存储合适的三角形的容器，而种子三角形的三条边就成为曲面S的初始边界∂S。于是，基于种子三角形及其边界，开始搜索合适的三角形添加到曲面S上。

1.2.4 约束条件

(1) 拓扑限制条件：为保证曲面S的可定向性，防止产生类似Mobius环的曲面，需要附加拓扑限制条件来筛选出相对正确的三角形。如图5所示，虚线表示待选三角形，记为T。e是T的三角形结构中的CE∈∂S，b是边e所对三角形顶点Pn，拓扑限制条件包含4种情况：①拓展，T的顶点b在曲面S外；②粘合，T的顶点b在边界∂S上，但b的两个邻边不在∂S上；③边界填充，T的顶点b在边界∂S上，但b只有一条邻边在边界∂S上；④孔洞填充，T的3条边都在边界∂S上。

图5 拓扑限制条件(A=拓展；B=粘合；C=边界填充；D=孔洞填充)Fig.5 Topological constraints(A=extension；B=gluing；C=ear filling；D=hole filling)

满足上述4种情况的三角形能够保证曲面的可定向性。需要特殊说明的是“粘合”这种情况，仅仅添加三角形T是不能保证可定向性的，因为顶点b作为一个边界点，在边界上与它相连的边的个数不止两个时，此点在边界上的导向就会出现错乱。为避免出现这种情况，添加三角形T的同时还需要添加一个特定的三角形T′(如图5中待选三角形B相邻的虚线部分)，T′与T是邻接关系。

(2) 半径限制条件：∂S是由边缘三角形的外侧边E构成的，每条E在DT中连接有多个三角形(图6)，要从中选择一个最合适的三角形作为候选三角形Tc。

图6 根据T∈S选择候选三角形TcFig.6 Select candidate triangle Tc according to T∈S

关于如何选择候选三角形Tc，这里需要引入一个结论：根据上文对半径参数rt的定义，可知rt是三角形中任意顶点到其对偶Voronoi图边界的距离，因为Voronoi图是基于狄洛尼三角形的各边中垂线构成的。从比较简单的二维光滑曲线重建来分析rt的意义，在采样点足够密集的时候，点集的Voronoi边界会收敛于曲线图形的骨架线(图7)。以图7中点P为例，与P相连的图形边界线中，正确的边界线往往是P连接相邻采样点的线段，长度也近似于点P到骨架线的垂直距离，而错误的边界线长度往往要大于这个数值。根据这一结论，在三维空间中半径越小的三角形越有可能构建正确的曲面。所以，每条E都选择半径最小的三角形作为这条边的候选三角形。边界∂S上的每条E都对应一个Tc，当然也有可能出现某条E不存在满足条件的候选三角形的情况，但那种情况较少，最终多个候选三角形组成一个集合，记为TU。

图7 狄洛尼三角剖分(a)及其对偶Voronoi图(b)，(c)为光滑曲线重建演示图，粗实线为其中轴线Fig.7 Delaunay triangulation (a) and its dual Voronoi diagram (b)，(c) for smooth curve reconstruction demo map，the heavy line for its skeleton line

1.2.5 三角形优劣等级

为从TU中选出最合适的三角形，需要赋予每个候选三角形一个评估参数，记为优劣等级L。此外，候选三角形是通过对比rt筛选得出，而rt是基于二维平面元素得到的，并未拓展到三维空间。为保证重建曲面的质量，还需要引入一个参数，即邻接三角形之间的二面角参数β。

如图8所示，T是曲面S边缘处的三角形，它所在平面的法向量记为N1，而与之相邻接的候选三角形Tc的法向量记为N2，N1、N2的夹角即是Tc的二面角参数β。β的大小直接影响到曲面局部的起伏，需要设定一个阈值α来筛选出β尽量合理的候选三角形。α的数值并不客观，初步设定为π/6。当β<α时，两三角面片之间的二面角被认为是在合理范围内，此时优劣等级L=1/rt；α<β<π-α时，L=-β；β>π-α时，此时二面角不在合理范围内，将β设定成一个足够小的值。所有候选三角形按照优劣等级降序排列，构成候选三角形序列Q，排位越靠前的三角形越先被添加。定性来讲，当Q中存在β小于α的三角形时，优先选择rt较小的三角形，不存在β小于α的三角形时，选择β较小的三角形。

图8 二面角示意图Fig.8 Schematic diagram of the dihedral angle

如图9所示，Tc1的二面角不在合理范围内，所以将其排除，Tc2、Tc3的二面角都在最合理的范围内，但是Tc3的半径最小，所以最合适的三角形是Tc3。Tc4只有在Tc2、Tc3这类三角形不存在的情况下才有可能被选，且优先选择二面角较小的三角形。

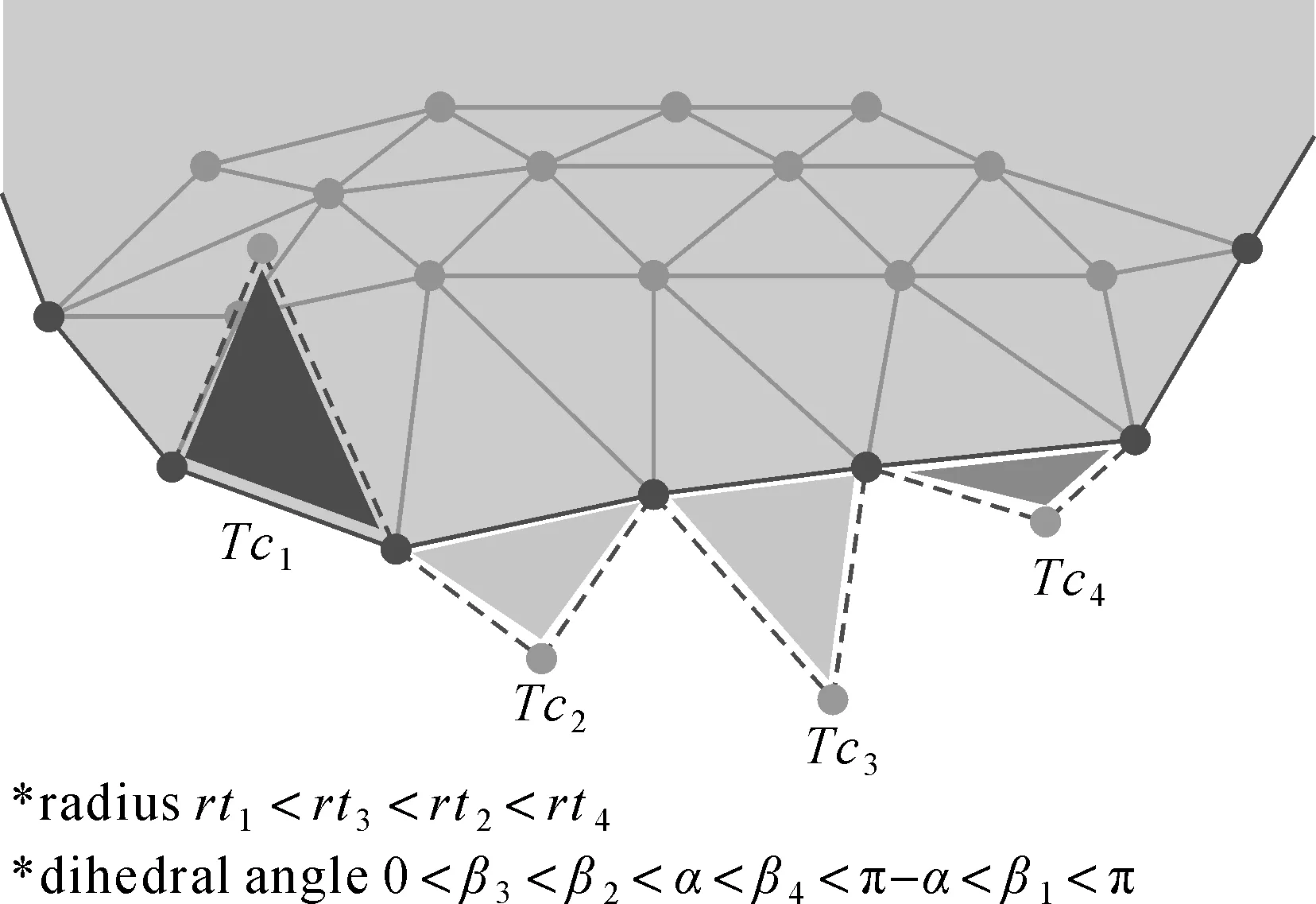
图9 最终三角形的选择Fig.9 Selection of the final triangle

2 算法实现

算法在重建曲面过程中，曲面边界∂S、候选三角形序列Q都随着曲面S的拓展而不断变化，添加新的三角形到曲面S上时，不同的拓扑情况需要不同的操作。对于“拓展”“边界填充”“孔洞填充”这3种情况，都会在曲面S上添加新的三角形，但是对于“粘合”这种情况却不一定。算法添加三角形的同时必须根据三角形符合的拓扑限制条件来更新Q。特别的是，对于“粘合”这种情况，只有存在邻接三角形对T′∪T且T′的优劣等级L大于T时才会执行添加操作。

算法的终止条件有两种：如果重建的曲面是闭合的，那么边界∂S中边的个数最终会为0，此时算法会终止循环输出曲面S；如果重建的曲面是不闭合的，那么添加边界三角形时会遇到“粘合”这种情况，如果“粘合”的三角形不符合三角形选择标准，那么算法会检验Q中的下一个三角形。如果边界内的平面已经充分重建，那么Q中的三角形全部不符合标准，当Q中最后一个三角形已被检验不符合后，算法就会跳出循环，输出曲面S，算法的具体实现如下伪代码所示。

surface reconstruction algorithm function

compute the 3D Delaunay triangulation DT of sample points;

{Initialization: compute the radius(rt) of triangles，initialize the seed triangletsand ∂S}

for all triangles of DT do compute thertof triangle

ts←t;

end if

end for

inserttsintoS;

insert 3 edges into ∂S，initialize theSand ∂S；

insert all the candidate triangles of edges of ∂SintoQ;

{surface extraction: add(T) means insertTintoSand return whether it is inserted successfully；c(E) means the candidate triangle of edgeE}

T← the first element ofQ;

do case = add(T);

if case = true，then

T← the first element ofQ;

end if

if case = false，then

removeTfromQ;

insert c(E) (exceptT) inQ;

T← the first element ofQ;

end if

if case = later，then

ifTis the last element ofQ，then

returnS;

end if

else

T← the first element ofQ;

end if

end while until the size of ∂Sis zero

returnS

算法中存在这样的一类三角形，即它的优劣等级L会被设置为一个足够小的数从而避免选择它，但是随着曲面形态的变化，这些三角形可能又会符合曲面整体的情况。对此，算法会重新计算它的优劣等级，更新候选三角形序列，从而添加最合适的三角形。此外，由于某些曲面信息过去复杂，依据标准不足以完全避免错误的三角形，但是这些三角形rt数值比较大，所以可以在三维狄洛尼三角剖分阶段通过设置一个阈值来去除过大的三角形。

3 数据处理结果与分析

目前，大部分曲面重建算法的重建效果都比较依赖于点云数据的质量，不同的算法可能适合不同的扫描状况，如Poisson曲面重建算法，除了点云的坐标信息外，还需要点云的法向信息，但是对于大部分采样点稀疏或者不均匀的点云数据来讲，法向信息是难以计算准确的。图10(a)是对模型充分扫描所得的点云，点云比较密集并且能够一定程度上反映模型的外形特征。但很多时候由于仪器设备、技术支持、扫描成本的制约，在实际生产过程中，可能无法获得扫描质量足够好的点云。例如，图10(b)点云相对于图10(a)就比较稀疏，并且圈选处的点云相对其他部位更为稀疏，整体点云的分布很不均匀。对于图10(b)这种质量较差的点云数据，利用Poisson算法重建出理想的模型还是相当困难的。即使是著名的Wrapping算法，重建此类模型也有不同程度的缺陷，如图10(c)。但是本文算法能够适应这种点云数据，并且重建出较好的模型质量，如图10(d)。

点云数据的稀疏和密集是相对于扫描模型本身而言，并没有明确的界定，但是质量较差的点云数据一般较为稀疏并且点云分布不均匀，有些可能还会出现数据缺失的现象。除此之外，大部分点云还会存在噪声数据，对于噪声点云的曲面重建，还需要利用专门的点云去噪算法[27]对点云数据进行预处理。所以，构造出适应性更强的算法也是曲面重建算法研究的重点。

图10 人体模型点云数据及其重建效果图Fig.10 The point cloud data and the reconstruction results of man model

3.1 曲面重建结果

本文在Intel® CoreTMi7-4790 CPU @ 3.60 GHz，RAM(16.0 GB),Windows 8.1 64位操作系统配置环境下，对曲面重建质量和效率进行测试。

3.1.1 地形扫描点云模型

扫描地形表面获取的三维点云数据可以用于生成DEM，而生成DEM的算法一般是将点云投影到二维平面上构建二维狄洛尼三角网，并在此基础上添加高程(图11(b))，与三维曲面重建算法是有本质区别的，由于投影的多值性(投影点对应多个Z值)，在表示陡峭的地形时，容易产生畸变。而本文算法按照约束条件构建最优曲面，较传统的DEM具有明显优势，如图11所示。

图11 某工程用地的三维点云数据及其表面模型Fig.11 The 3D point cloud data and its surface model for an construction site

3.1.2 建筑物扫描点云模型

建筑物扫描点云的数据量大，质量较差，无法构建精细的曲面模型。针对大数据量的点云，本文算法首先利用所有点云生成自适应八叉树，再基于八叉树对点云进行空间分割，然后依次在各个分块点云中启动算法。相邻的分块点云完成曲面重建时，由于相邻曲面满足“粘合”拓扑限制条件，所以再次重启算法以完成曲面的拼接，最终获得整体重建的曲面，如图12所示。

3.1.3 精细化扫描点云模型

精细化扫描主要应用于文物保护，这类点云模型采样点的密度和数量较大，细节较多，形态构造较为复杂。图13为3个精细化扫描点云模型的曲面重建结果。

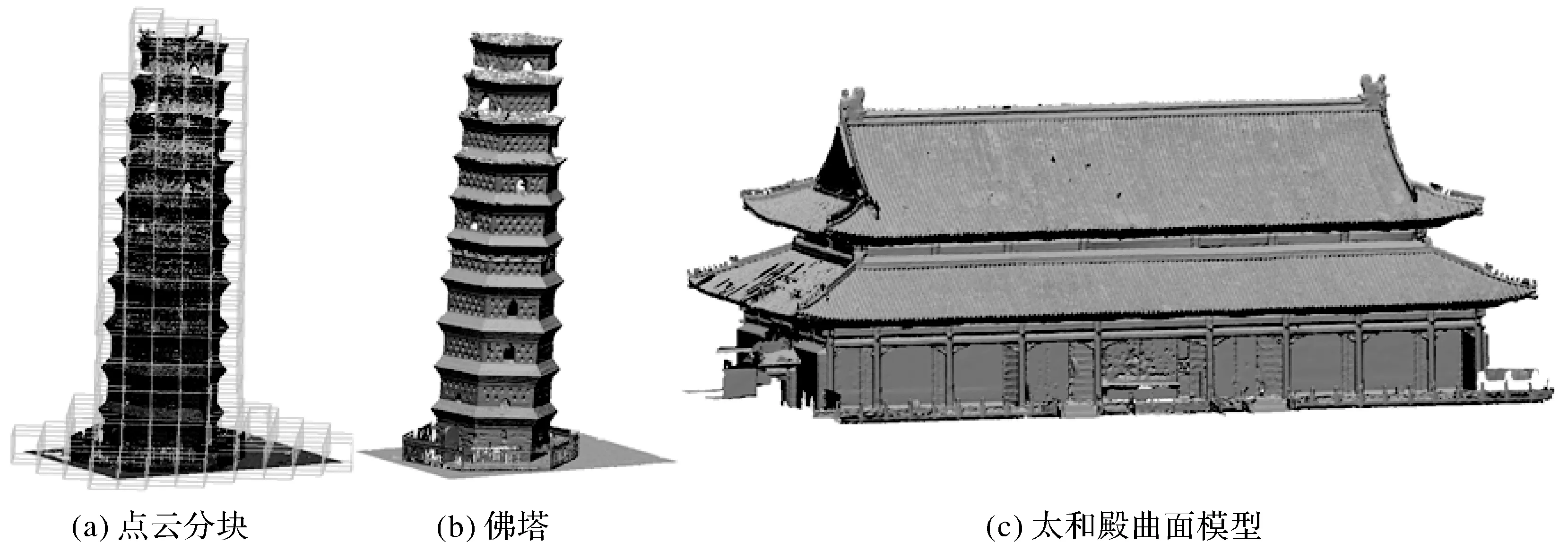
图12 建筑物扫描点云重建表面模型Fig.12 Reconstruction surface model of building scanning point cloud

图13 精细化扫描点云重建表面模型Fig.13 Fine scanning point cloud reconstruction surface model

3.2 时间统计与结果分析

如表1所示，本算法的重建效率对比DBRG算法有一定的优势，但逊于Poisson曲面重建算法，而Poisson曲面重建算法无法正确重建人体和太和殿点云模型。

表1点云模型点数、对应三维狄洛尼三角形数及重建时间

Tab.1Thenumberofpointsofpointcloudmodels，thenumberoftrianglesintheir3DDelaunaytriangulationandrunningtimes

modelpointsDelaunaytriangulationt1t2tDBRG:tPoisson:t人体 174951374330.091.221.311.35×建筑工地2490573214571.1722.6323.8024.134.87龙形神兽43765462914003.8845.7149.5953.1726.72佛像54365277420914.7669.7374.4980.4327.12柱状文物12374536764956721.72293.07314.79332.6673.24太和殿55772531229753841.75998.361040.111462.63×佛塔56339251087363637.12974.241011.361543.72372.21

注：t1=construction of 3D Delaunay triangulation

t2=main function of surface reconstruction

t=total running time

DBRG:t=the total running time of DBTG algorithm[24]

Poisson:t=the total running time of Poisson algorithm[11]×=failed reconstruction

算法重建效率方面，Poisson曲面重建算法依赖于法线的计算，而计算点云法线以及法线一致性[28]也具有一定的时间复杂度，有时法线计算的时间可能会远远大于曲面重建的时间，而且存在某些模型的法线无法定向。此外，Poisson曲面重建算法是通过曲面拟合实现重建，生成的曲面与原始点云存在偏离现象，需要调整相关参数来提高重建精度，而本算法生成的曲面三角网本身就是由原始点云构造的三角形组成的，每个原始点均在曲面上，故不存在点位精度问题。在算法适应性方面，本算法能够适应除植被扫描点云模型外的多种点云模型，而Poisson曲面重建算法对于人体模型、太和殿这种无法定向法线的点云模型则无法完成重建，并且重建带有边界的点云模型还需要经过裁剪才能达到最终效果，重建过程较为复杂。

4 结 论

本文算法通过构建三维狄洛尼三角网，按照拓扑、半径约束条件从中选取候选三角形，再根据半径参数和二面角参数计算优劣等级，从而不断选出最优三角形添加到生长曲面上。经过试验测试，结论如下：

(1) 本算法能够适应包括地形扫描、建筑物扫描和精细化扫描在内的多种点云模型，算法适应性强；

(2) 重建曲面的细节纹理还原度较高，曲面质量好；

(3) 对比常用的显式和隐式曲面重建算法都具有一定优势，实用性较强。

但本算法也存在不足，如无法应对噪声数据，建模前需做滤波处理；针对大规模点云数据三维重建的时间复杂度需进一步优化，研究结合并行计算的数据分块算法以提高算法的整体效率。

[1] BOISSONNAT J D. Geometric Structures for Three-dimensional Shape Representation[J]. ACM Transactions on Graphics (TOG), 1984, 3(4): 266-286.

[2] TURK G, O’BRIEN J F. Shape Transformation Using Variational Implicit Functions[C]∥Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 1999: 335-342.

[3] TURK G, O’BRIEN J F. Modelling with Implicit Surfaces that Interpolate[J]. ACM Transactions on Graphics (TOG), 2002, 21(4): 855-873.

[4] ZHAO Hongkai, OSHER S, MERRIMAN B, et al. Implicit and Nonparametric Shape Reconstruction from Unorganized Data Using a Variational Level Set Method[J]. Computer Vision and Image Understanding, 2000, 80(3): 295-314.

[5] PARK S H, LEE S S, KIM J H. A Surface Reconstruction Algorithm Using Weighted Alpha Shapes[M]∥WANG Lipo, JIN Yaochu. Fuzzy Systems and Knowledge Discovery. Berlin: Springer, 2005: 1141-1150.

[6] BOISSONNAT J D, CAZALS F. Smooth Surface Reconstruction via Natural Neighbour Interpolation of Distance Functions[J]. Computational Geometry, 2002, 22(1-3): 185-203.

[7] MEDIONI G, LEE M S, TANG C K. A Computational Framework for Segmentation and Grouping[M]. New York, NY, USA: Elsevier, 2000: 243-253.

[8] DIGNE J. An Implementation and Parallelization of the Scale Space Meshing Algorithm[J]. Image Processing On Line, 2015, 5: 282-295.

[9] LHUILLIER M. Overview of Shelling for 2-manifold Surface Reconstruction Based on 3D Delaunay Triangulation[J]. Journal of Mathematical Imaging and Vision, 2017, 59(2): 318-340.

[10] MERRY B, GAIN J, MARAIS P. Moving Least-squares Reconstruction of Large Models with GPUs[J]. IEEE Transactions on Visualization and Computer Graphics, 2014, 20(2): 249-261.

[11] KAZHDAN M, BOLITHO M, HOPPE H. Poisson Surface Reconstruction[C]∥Proceedings of the 4th Eurographics Symposium on Geometry Processing. Cagliari, Sardinia, Italy: Eurographics Association, 2006: 61-70.

[12] KAZHDAN M, HOPPE H. Screened Poisson Surface Reconstruction[J]. ACM Transactions on Graphics (TOG), 2013, 32(3): 29.

[13] BOLITHO M, KAZHDAN M, BURNS R, et al. Multilevel Streaming for Out-of-core Surface Reconstruction[C]∥Proceedings of the 5th Eurographics Symposium on Geometry Processing. Barcelona, Spain: Eurographics Association, 2007: 69-78.

[14] LIU Shengjun, WANG C C L, BRUNNETT G, et al. A Closed-form Formulation of HRBF-based Surface Reconstruction by Approximate Solution[J]. Computer-aided Design, 2016, 78: 147-157.

[15] YANG Long, YAN Qing’an, XIAO Chunxia. Shape-Controllable Geometry Completion for Point Cloud Models[J]. The Visual Computer: International Journal of Computer Graphics, 2017, 33(3): 385-398.

[16] LORENSEN W E, CLINE H E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm[J]. ACM SIGGRAPH Computer Graphics, 1987, 21(4): 163-169.

[17] SCHAEFER S, JU Tao, WARREN J. Manifold Dual Contouring[J]. IEEE Transactions on Visualization and Computer Graphics, 2007, 13(3): 610-619.

[18] EDELSBRUNNER H. Surface Reconstruction by Wrapping Finite Sets in Space[M]∥ARONOV B, BASU S, PACH J, et al. Discrete and Computational Geometry. Berlin: Springer, 2003: 379-404.

[19] DIGNE J, MOREL J M, SOUZANI C M, et al. Scale Space Meshing of Raw Data Point Sets[J]. Computer Graphics Forum, 2011, 30(6): 1630-1642.

[20] FUHRMANN S, GOESELE M. Floating Scale Surface Reconstruction[J]. ACM Transactions on Graphics (TOG), 2014, 33(4): 46.

[21] AN Yi, ZHAO Peng, LI Zhuohan, et al. Self-adaptive Polygon Mesh Reconstruction Based on Ball-pivoting Algorithm[J]. International Journal of Computer Applications in Technology, 2016, 54(1): 51-60.

[22] BOISSONNAT J D, CAZALS F. Smooth Surface Reconstruction via Natural Neighbour Interpolation of Distance Functions[C]∥Proceedings of the 16th Annual Symposium on Computational Geometry. Hong Kong, China: ACM, 2000: 223-232.

[23] COHEN-STEINER D, DA F. A Greedy Delaunay-based Surface Reconstruction Algorithm[J]. The Visual Computer: International Journal of Computer Graphics, 2004, 20(1): 4-16.

[24] KUO Chuanchu, YAU H T. A Delaunay-based Region-growing Approach to Surface Reconstruction from Unorganized Points[J]. Computer-Aided Design, 2005, 37(8): 825-835.

[25] TEILLAUD M. Three Dimensional Triangulations in CGAL[C]∥Abstracts 15th European Workshop Computational Geometry. [S.l.]: INRIA Sophia-Antipolis, 1999: 175-158.

[26] SI Hang. Three Dimensional Boundary Conforming Delaunay Mesh Generation[D]. Berlin: Technische Universität Berlin, 2008.

[27] PARK M K, LEE S J, JANG I Y, et al. Feature-aware Filtering for Point-set Surface Denoising[J]. Computers & Graphics, 2013, 37(6): 589-595.

[28] BOULCH A, MARLET R. Fast and Robust Normal Estimation for Point Clouds with Sharp Features[J]. Computer Graphics Forum, 2012, 31(5): 1765-1774.