基于多项式迭代的等效旋转矢量微分方程精确数值算法

严恭敏，李思锦，秦永元

（西北工业大学 自动化学院，西安 710072）

在捷联惯导算法中，目前主流的姿态更新求解方法是先使用陀螺角增量（或角速率）的多子样采样计算等效旋转矢量，补偿转动不可交换误差，再使用等效旋转矢量计算姿态更新四元数[1-6]。但是传统多子样算法都是在等效旋转矢量微分方程（Bortz方程）二阶近似的基础上进行推导的，从源头上看不可避免地存在原理性误差，使得在大机动环境下选用子样数越多，精度往往越差[7]。

最近，数位研究者注意到了传统多子样算法存在的缺陷，提出了一些改进的新算法。文献[8-9]考虑了Bortz方程中三阶甚至四阶项的影响，提出一种改善算法精度的方法，增加了角增量的三阶和四阶叉乘项进行不可交换误差补偿，但是该方法的推导过程比较繁琐，难以扩展到五阶及以上叉乘运算，原理上精度受限。文献[10]提出基于四元数微分方程迭代的姿态更新算法，文献[11]提出基于罗德里格参数微分方程迭代的姿态更新算法，两者除了使用的数学描述工具不同外，其总体设计思路基本一致，都是在假设角速度为多项式的条件下，通过迭代计算能够精确给出姿态更新的数值解。相比而言，前者在表示形式上更为简洁且计算量稍少一些。类似于上述两种迭代算法，本文将利用Bortz微分方程给出基于多项式迭代的等效旋转矢量精确数值算法，有效避免了原理性近似误差。同时，本文对算法的精度和和收敛速度进行了分析。研究结果表明，与四元数迭代方法相比，新算法具有同样的数值计算精度，且计算量相当，具有较好的应用价值。

1 算法理论分析

1.1 迭代算法推导

等效旋转矢量微分方程（Bortz方程）为[1]

其中，ω为动坐标系相对于参考坐标系的转动角速度矢量，φ=φ为等效旋转矢量φ的模值。将式(1)中的余切函数作泰勒级数展开，经整理后可得：

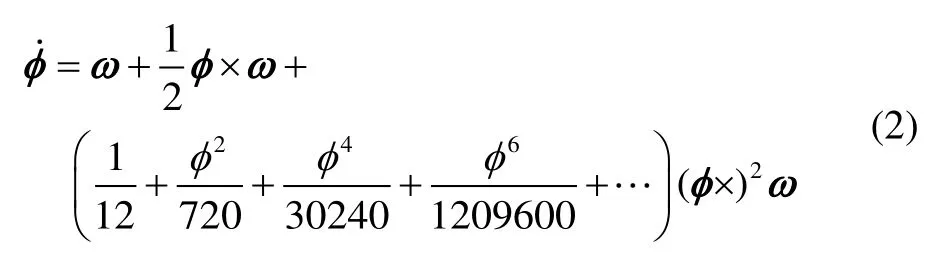
式(2)两边同时在时间区间[0,t]上积分，得：

将式(3)左边φ(0)移到右边，并改写成迭代的形式，有：

其中，φ(i)(i=0,1,2,…)表示第i次迭代的等效旋转矢量，且有迭代初值φ(0)=0。不失一般性，可令初值φ(0)=0。

假设角速度ω为时间t的有限次（N-1次）多项式：

如果实际陀螺采集的为N子样的角增量数据，则可先按文献[10]的方法变换为上述角速度多项式，再使用本文方法。

再假设经过第i次迭代后的等效旋转矢量φ(i)多项式为

注意到式(4)中φ(i+1)为多项式的积分，因而φ(i+1)（或φ(i)）的多项式零次项系数必为 0，即有

将式(5)和式(6)代入式(4)右端的被积函数各项中作进一步计算，有：

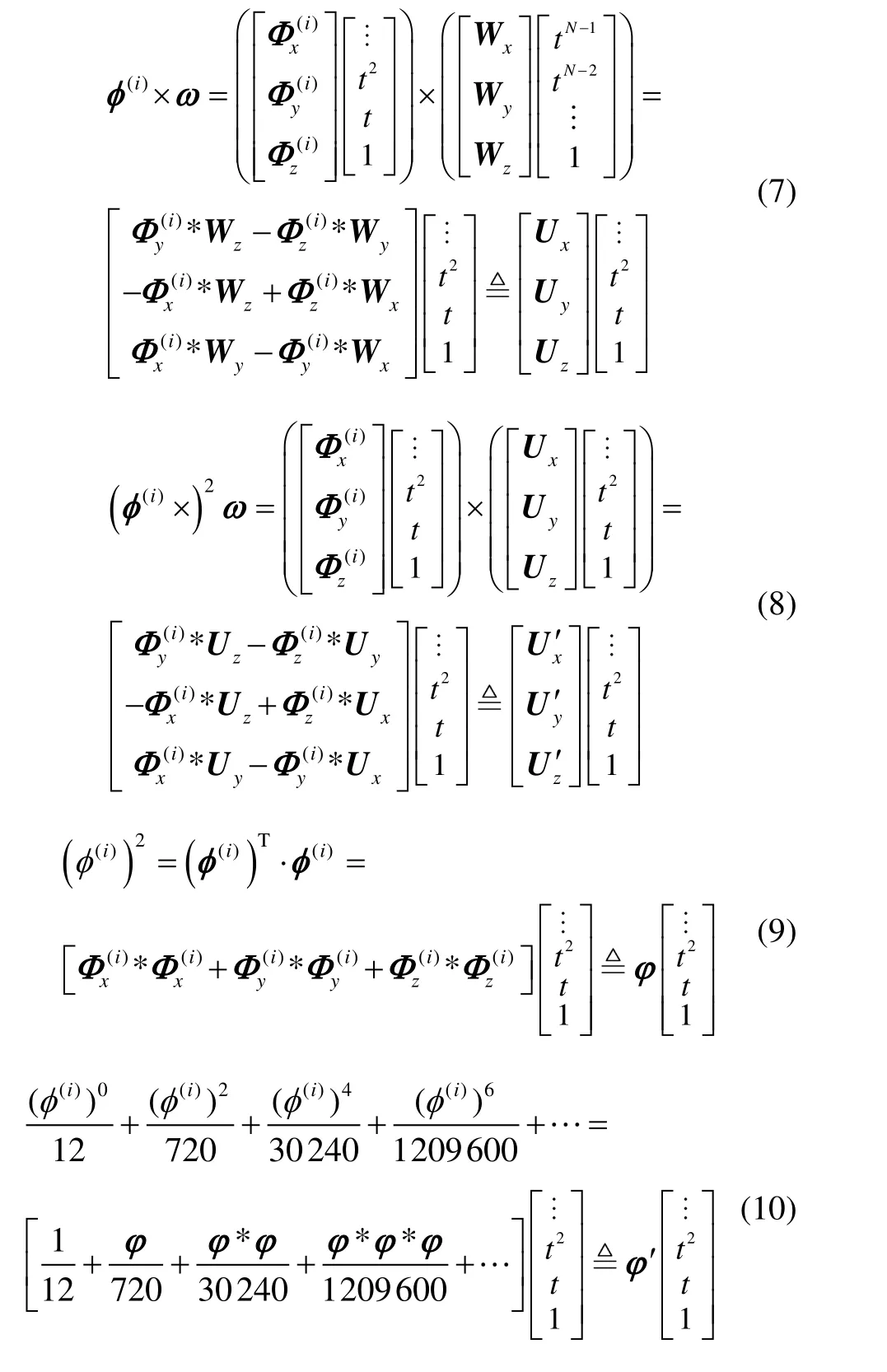
其中，运算符“*”表示两个多项式系数向量之间的卷积运算。

再将式(5)(7)(8)(10)代入式(4)，可得：

1.2 精度分析

在实际利用计算机进行求解时，需对式(4)中的余切函数展开取有限阶次。一般角速度的零次项多项式系数不为0，则当迭代次数时，多项式的不为 0的最低幂次为 1。如果存在不可交换误差，的多项式表示系数中不为 0的最低幂次一般为2不为0的最低幂次为3不为0的最低幂次为()。因此，若忽略了式(4)右端被积函数中与模值有关的不小于的所有项，则将可能影响被积函数次幂的计算准确性，再经过积分之后等效旋转矢量多项式的阶精度会受到影响。换句话说，若忽略及其以上项后，等效旋转矢量的多项式解在理论上只具有阶精度。

作为对比，传统的基于等效旋转矢量泰勒级数展开法的多子样算法是在如下近似公式(14)的基础上作进一步推导的。

在保留余切函数展开无穷幂次的情况下，式(4)理论上是严格成立的，即对于均成立。但如果仅保留有限幂次，为了保证等式近似程度足够高，必须使余切函数展开的高幂次项迅速衰减，以至于在数值计算上误差可以忽略不计。

式(15)可近似为（实际上是条件变严格了）：

由式(16)求解得：

这意味着，在更新周期[0,t]内，如果等效旋转矢量模值（可近似为角增量模值变化）小于 3.3°，则在计算时可忽略及更高幂次项的影响。

1.3 计算量分析

传统机械设计作业中主要存在的问题之一即为：设计成本较高。具体分析设计成本高主要体现为：设计产品通过生产线进行生产制造，并基于实际生产的机械设备进行性能，质量等基础参数的测试。实际测试中如出现问题则需重新生产制造，从而造成了设计成本高的现象。分析自动化技术在应用中通过在线模拟测试的方式，有效的对机械装置的力学性能，结构安全性，进行了完善的测试和评估。后期结合3D打印技术进行相关设计成果的制造，有效的降低了生产线生产产生的高设计成本现象。

2 仿真验证

2.1 圆锥运动误差仿真

圆锥运动和多项式角运动常常用来评价姿态更新算法的精度优劣，下面也采用圆锥运动环境来对比本文算法与传统优化圆锥算法的姿态解算精度。

图1 圆锥运动算法误差对比Fig.1 Comparison on algorithm errors of coning motion

从图1中可以看出，传统算法在锥轴上的漂移误差逐渐变大，在1 s时为0.1″，在非锥轴上的误差呈周期性变化，最大达到了5″；而新算法的三轴误差始终都很小，经放大观察仅为10-7″量级。这说明，如果出现不规则非整周期的圆锥运动，传统算法可能会引起较大的姿态解算误差，而新算法能近乎完美的解算复现真实的姿态运动，新算法对于复杂的角运动具有非常高的求解精度。

进一步仿真表明，本文算法与文献[10]所提的四元数迭代算法具有同等数值精度，更多的仿真情况可参考文献[10]，这里不再赘述。

2.2 迭代收敛性仿真

表1 各阶多项式系数误差收敛特性Tab.1 Convergence of polynomial coefficient errors

由表1可见：第1次迭代后，2阶项系数误差为0（收敛）；之后每增加1次迭代，收敛阶数加1；经过6次迭代后，7阶项系数完全收敛。这表明，等效旋转矢量迭代收敛的速度是很快的，从而决定了算法的计算量不是太大。

3 与罗德里格参数迭代法的对比讨论

同Bortz方程(1)的结构相似，罗德里格参数微分方程为[11]

前文1.1节分析的迭代方法也可应用于式(21)，迭代公式为

采用式(22)迭代的优点是不含三角函数运算，计算量会比式(4)更少（约减少三分之一）。此外，在实际计算时式(4)需截取余切函数的有限项，使得存在如式(17)所示的角速度范围限制，而式(22)在理论上对任意角速度都是迭代收敛的。

仿真还表明，迭代式(22)也具有如表1所列的收敛特性。当然，与罗德里格参数表示相比，采用等效旋转矢量的优点是物理意义更直观，方程(21)右端的第三项意义不够直观，而方程(1)右端的第二、三项均表示不可交换误差，所以本文关于等效旋转矢量迭代的研究结果容易直接与很多已有的传统多子样算法成果进行对比。

4 结 论

传统圆锥误差补偿算法在纯圆锥运动环境下且半锥角比较小时是非常有效的，然而对于大锥角情况或者应用于大角度机动环境，都会产生较大的姿态漂移误差。

为了避免这一问题，本文根据Bortz方程构造了多项式积分迭代公式，给出了一种新的直接求解等效旋转矢量的数值算法，在算法推导过程中考虑了不可交换误差高阶项的影响，算法计算精度高，具有与四元数微分方程迭代解相同的数值精度[10]。通过与传统的基于等效旋转矢量的多子样算法对比仿真，验证了新算法在大幅值圆锥运动条件下具有明显的精度优势。新算法的计算量较小，具有较好的应用价值。