基于伪标准差和N-P准则的行人导航零速检测
戴洪德,李松林,周绍磊,全闻捷
(海军航空大学,烟台 264001)
在楼宇消防、单兵作战、井下工作等环境下,为行人提供准确可靠的导航信息直接关系到任务的完成,甚至关系到人员的生命安全。基于全球卫星定位系统(GPS)的导航系统具有全时、全球导航,用户终端便宜、导航可靠、精度高等优点,在全球范围内获得了最为广泛的应用。但是GPS信号容易被楼宇、树林等遮挡,不适应室内、丛林、地下等导航环境。因此,在行人导航中不能过于依赖卫星导航系统。为此,相继出现了基于超声波、蓝牙、LED 灯光、ZigBee、WIFI、RFID等[1-4]室内定位方式,能够实现较高精度的室内导航,但这些定位方式需要提前在室内安装相当数量的发送/接收设备,成本比较高,不适应大范围的导航需求。
基于微型惯性测量单元(Miniature Inertial Measurement Unit,MIMU)的行人导航系统具有体积小、重量轻,能够利用自身设备实现自主连续导航的优点[5-6]。但是该系统具有误差随时间积累的缺点,长时间的使用会造成较大的导航误差,如何来减小导航误差成为了该领域研究的重点。零速修正(Zero Velocity Update,ZUPT)是常用的减小行人导航误差的方法[7],能准确判断行人行走过程中的零速区间,是零速修正的前提。利用MIMU自带的传感器进行零速检测是目前行人导航常用的方法。一些文献利用采样窗口内三轴陀螺仪的极差以及加速度计模值的最大值与设定阈值作比较,并经过“或”运算判断零速区间[8],降低了漏判概率,但是增加了误判概率。行走速度比较快时,该方法误差增大。一些学者利用加速度计、陀螺仪输出值得到其模值、标准差并与阈值作比较作为零速检测判定条件[9]。一些文献利用加速度峰值和角速度能量进行零速检测[10]。这些方法均需要进行多次比较,而且需要根据步速来调整阈值。这是由于这些传感器数据的统计量在零速区间和非零速区间的区分度不够造成的。本文定义了一个陀螺仪模值的伪标准差,使得零速区间和非零速区间在这个伪标准差的描述下区分度变大,并利用一个基于N-P准则的判别规则和一个固定阈值就能够适应不同行人从慢走到慢跑的多步态零速检测,不仅提高了零速检测的精度,而且简化了算法复杂度。
为验证本算法合理性与准确性,在3名实验者多种速度行走实验下,分别进行了固定阈值下的三轴陀螺仪极差+加速度计模值最大值检测法[8],“加速度计模值+加速度计标准差+陀螺仪模值+陀螺仪标准差”检测法[11]以及本文提出的基于伪标准差和N-P准则的零速检测方法的对比实验,实验结果表明本文方法简单有效,检测精度最高。
1 行走步态分析与特征提取
行人在行走过程中存在周期性的步态更迭,本文把每个周期分为两个区间,一个是全脚掌着地时的零速区间,另外一个是包括抬脚跟、空中摆动和脚跟着地的非零速区间。安装在脚跟的 MIMU的输出数据会呈现出与行走频率一致的周期性变化,图1表示的是一次行走中两个区间对应的三轴陀螺仪输出。
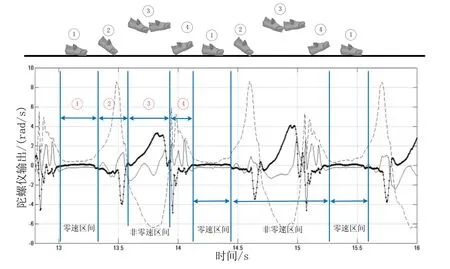
图1 行走步态分析Fig.1 Analysis of walking gait
通过图1可以明显看出,在零速区间内,由于脚的姿态保持不变,三轴陀螺仪的输出相对于非零速区间有两个数学特征:第一个是输出幅值接近于零,也就是一小段区间内的均值接近于零;第二个是输出幅值的波动较小,也就是一小段区间内的标准差较小。
1.1 步态在二维特征空间中的描述
对陀螺仪的输出进行求模处理:
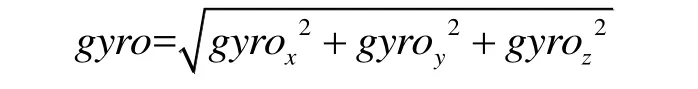
由于模值包含了三个轴向陀螺仪的输出信息,所以三轴陀螺仪模值的特性与其幅值的一些特性一致,如图2所示。相对于非零速区间,在零速区间内,陀螺仪模值的均值接近于零,陀螺仪模值的波动较小,也就是一小段区间内模值的标准差较小。
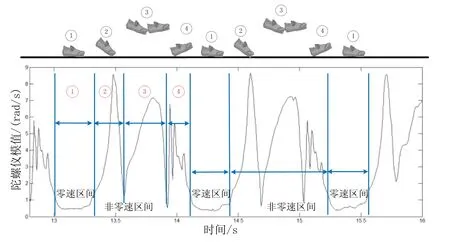
图2 三轴陀螺仪模值Fig.2 Mode value of three-axis gyroscope
利用采样窗口内陀螺仪模值的均值和标准差作为二维特征量并构成二维特征空间,如图3所示。在二维特征空间中,零速区间对应均值和标准差都较小的区域,而非零速区间则对应二维特征空间的其他区域。

图3 二维特征空间Fig.3 Two-dimensional feature space
1.2 伪标准差的构造及其意义
假设第i个采样点陀螺仪的模值为:
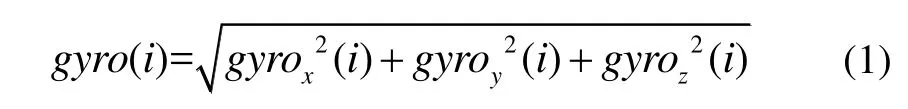
以第i个采样点为中心,选取一个采样窗口[i-s,i+s]。对采样窗口内的陀螺仪模值曲线用该曲线(i,gyro(i))点处的切线段近似,这样采样窗口内陀螺仪模值就可以表示为:

其中,k=gyro′(i)为陀螺仪模值曲线在采样中心i时刻的导数。
1)标准差
对采样窗口内的陀螺仪模值求标准差,采样窗口内由陀螺仪模值构成的数列为:
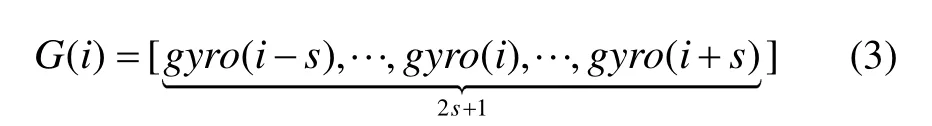
数列的均值为:
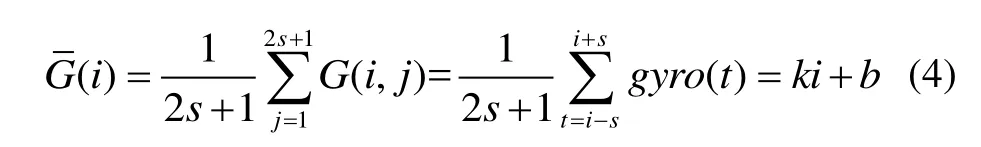
数列的标准差为:
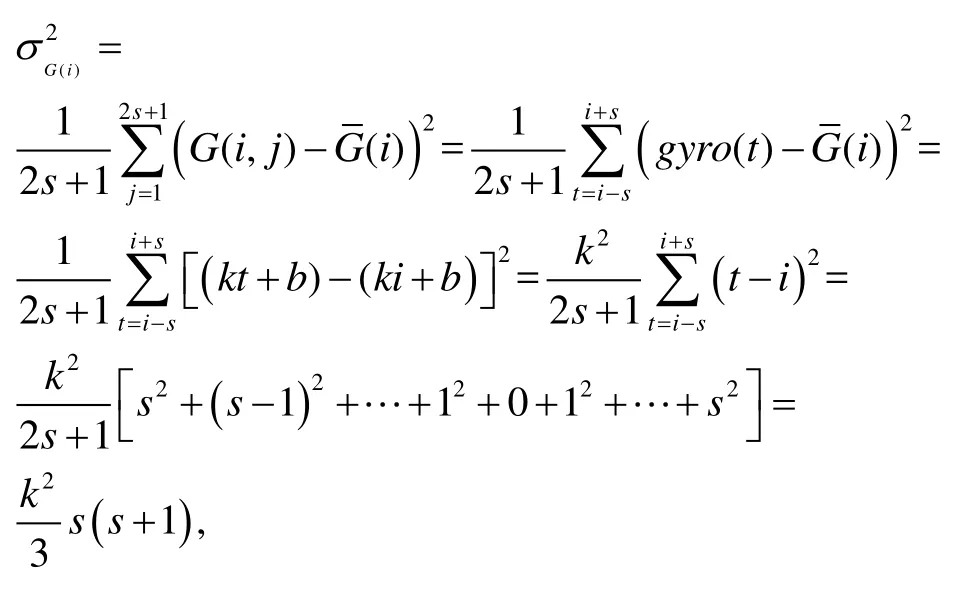

从标准差的表达式可以看出,当窗口大小一定时,标准差的大小与陀螺仪模值曲线在采样中心i时刻导数的绝对值成正比,而导数反映了数据的变化程度,所以标准差的大小反映了采样窗口内陀螺仪模值的变化程度,即波动程度,这与标准差的数学意义相符。
2)伪标准差
本文定义一个伪标准差,在以第i个采样点为中心的2s+1个模值中插入2s+1个0,构成一个扩充数列:
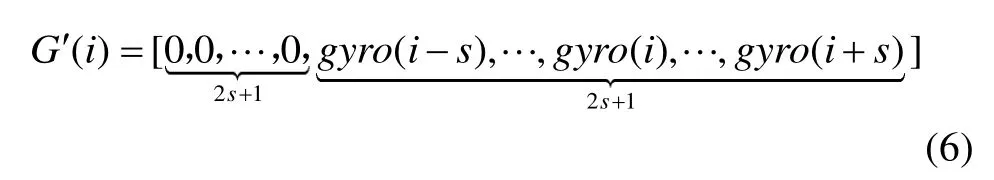
扩充数列的均值为:
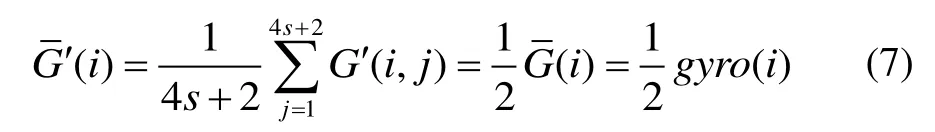
扩充数列的标准差为:

将这个扩充数列的标准差称为原采样窗口内陀螺仪模值的伪标准差。从伪标准差的表达式可以看出,当窗口大小一定时,伪标准差的大小不仅与螺仪模值曲线在采样中心i时刻导数相关,还与i时刻陀螺仪的模值的大小相关。由式(4)可以看出,gyro(i) 也是采样窗口内陀螺仪的均值。所以伪标准差不仅仅反映了采样窗口内陀螺仪模值的波动程度,还反映了采样窗口内陀螺仪模值的均值大小。从伪标准差可以看出,当且仅当采样窗口内陀螺仪模值的波动程度和均值都较小时,伪标准差的值才较小。分析陀螺仪模值图可以发现,只有零速区间内的采样窗口满足陀螺仪模值的波动程度和均值都较小的条件,所以只有零速区间内的伪标准差较小,而非零速区间内的伪标准差都较大。
陀螺仪模值的波动程度和均值这两个描述行走步态的特征量被融合到一个公式里面,使得伪标准差同时具有这两方面的数学特征。但是伪标准差的意义不仅在于它将两个描述行走步态的特征量融合到了一个公式里面,伪标准差更重要的意义在于增大了零速区间和非零速区间区分度。利用传统多条件零速检测的方法是通过提取行走过程中传感器输出的多个特征量,并通过设定相应阈值,来进行零速区间检测。这些特征量是单独存在的,这些特征量的增多并没有对零速区间与非零速区间的区分度有任何影响。而伪标准差将陀螺仪模值的两种特征量融合到一起,不是一般意义上的特征量的数量增多,而是提出了一个新的特征量——伪标准差,在这个特征量的描述下,零速区间与非零速区间的区分度得到提高,从而减小了零速检测中误判和漏判的概率,这与多条件的零速检测方法在原理上存在根本差异。
为了验证伪标准差的意义,本文将伪标准差与标准差对零速区间区分度的大小作对比。具体做法为,将多次不同步速的实测行走实验数据人为划分为零速区间和非零速区间,如图2所示,在相同实验数据、相同的区间划分下,对陀螺仪模值分别求标准差和伪标准差,并画出它们的概率密度曲线,如图4所示。图4中上图为标准差的概率密度曲线,下图为伪标准差的概率密度曲线。
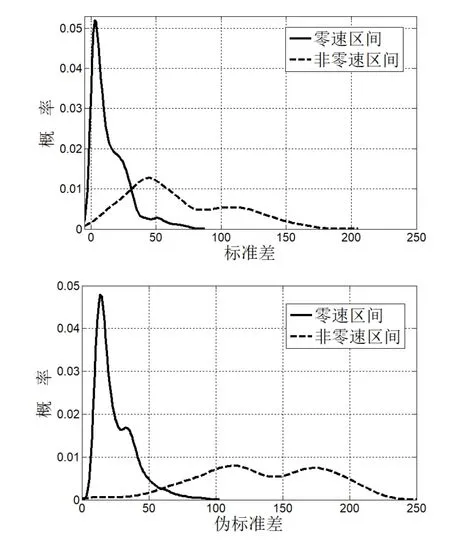
图4 概率密度曲线Fig.4 Probability density curve
对比两图可以发现,标准差中的两条概率密度曲线相交区域的面积大,说明其误判和漏判的概率大;而伪标准差中的两条概率密度曲线相交区域的面积小,误判和漏判的概率小。在标准差的坐标中,两条概率密度曲线出现波峰的位置很近,说明零速区间和非零速区间的区分度不够;而伪标准差的坐标中,两条概率密度曲线出现波峰的位置更远,说明零速区间与非零速区间的区分度更大。相对于陀螺仪模值标准差,利用伪标准差来描述步态,使得零速区间与非零速区间的区分度得到提高,这样零速检测更加容易,准确率也能够大大提高。
1.3 步态在一维特征空间中的描述
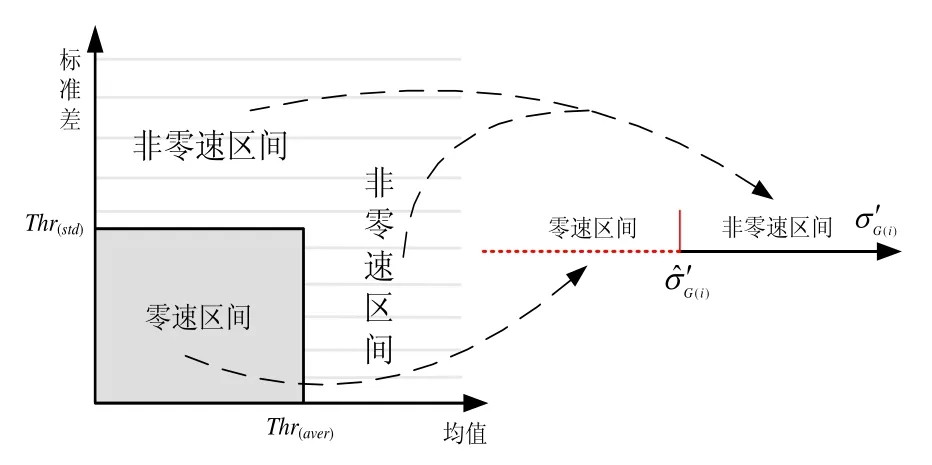
图5 一维特征空间Fig.5 One-dimensional feature space
2 基于N-P准则的零速检测
基于N-P准则的决策方法不需要知道类别的先验概率,只需要知道类别的概率密度函数[12],本文利用N-P准则推导在伪标准差构成的一维特征空间中进行零速检测这个二分类问题的判别规则。
为方便计算,本文将零速区间和非零速区间的两条伪标准差概率密度曲线相交的一小段区间到各自概率减小方向的概率密度曲线由两个正态概率密度函数来近似,即,如图6所示。
从图6可以看出,用正态概率密度函数近似后,错检或漏检的概率和原来基本一致,其中,虚线表示原概率密度曲线,实线表示正态概率密度函数,表示零速区间,表示非零速区间。这两个正态概率密度函数的参数是通过极大似然法估计得到的。
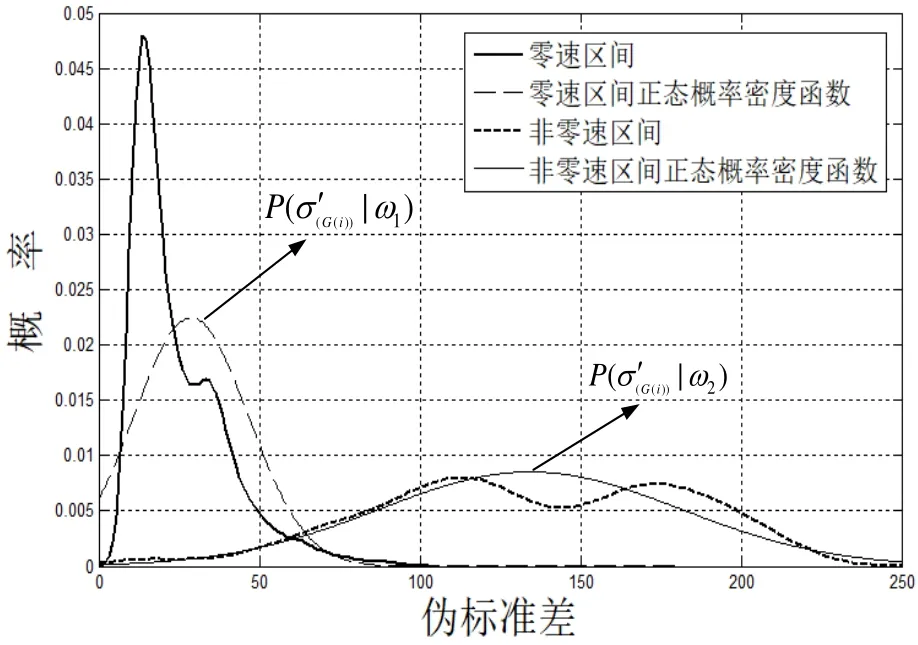
图6 概率密度近似Fig.6 Approximation of probability density
N-P准则的基本思想是保证漏检(或者错检)概率一定的情况下,使得错检(或者漏检)概率最小。本文规定将零速区间判断为非零速区间为漏检,表示为P1(e),反之为错检,表示为P2(e),如图7所示。

图7 正态概率密度函数Fig.7 Normal probability density function
由N-P准则,在限定ω1类错误率P1(e)的条件下,使ω2类错误率P2(e)最小,即:

利用Lagrange乘子法计算极值点:

将L(σG′(i),λ)分别对λ、σG′(i)求偏导得到:
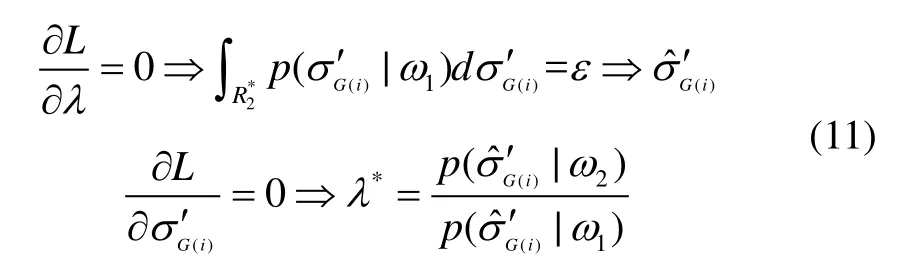
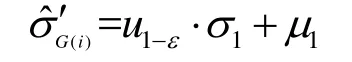
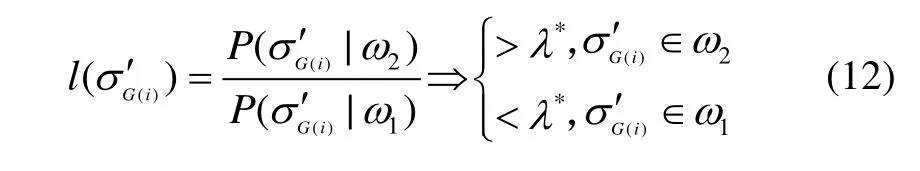
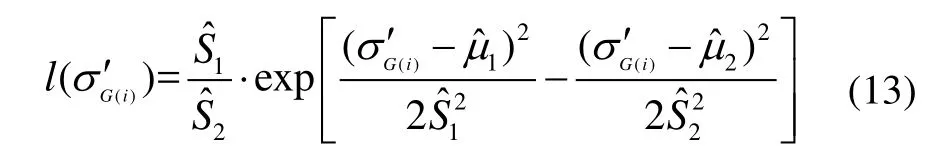

所以l(σG′(i))在上单调递减,在上单调递增,而所以所以()lσ′()G i函数曲线如图8表示。
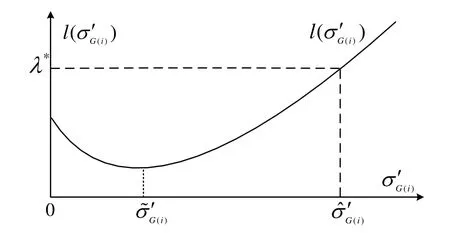
图8 l(σ G′( i))函数Fig.8 l(σ G′( i))function
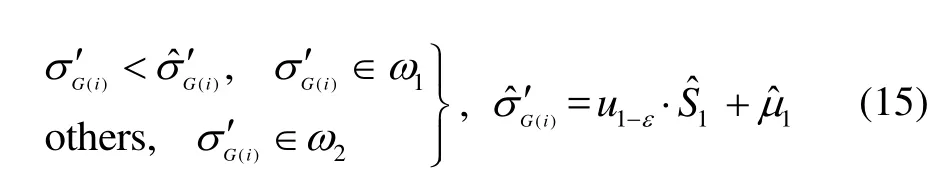

图9 基于伪标准差和N-P准则的零速检测流程图Fig.9 Flow chart of zero-velocity detection
3 实验验证
通过多次不同步速的陀螺仪数据计算得到零速区间伪标准差的均值和方差,根据极大似然法估计得到(°)/s,(°)/s,选取,查表得到2.88,根据式(15)可以得到:

选择3名志愿者进行零速检测实验,将MIMU安装在实验者脚跟部位,沿100 m的直线路程行走,并进行多次不同步速的行走实验,并分别利用三种方法进行零速检测。方法一:三轴陀螺仪极差+加速度计模值最大值检测法[8];方法二:加速度计模值+加速度计标准差+陀螺仪模值+陀螺仪标准差检测法[11];方法三:基于伪标准差和N-P准则的检测法。得到的实验结果如表1所示。
从实验结果可以看出,在行走速度小于5 km/h的时候,三种方法对3名实验者均能够达到较高的检测精度,但是在慢跑和跑步步态下,固定阈值下的方法一和方法二检测精度均大大降低,只有方法三还能够有效进行零速检测,说明方法三对不同速度的适应性很好。在慢跑和跑步步态下,方法二对实验者 A、C的检测精度比方法一高,但是方法二对实验者B的检测精度比方法一低,说明方法一和方法二对不同行人的适应性不好,而方法三对3名实验者的检测精度基本相同,说明方法三对不同行人的适应性比较好。在进行的综合实验中,方法三的零速区间平均检测精度达到了99.67%。
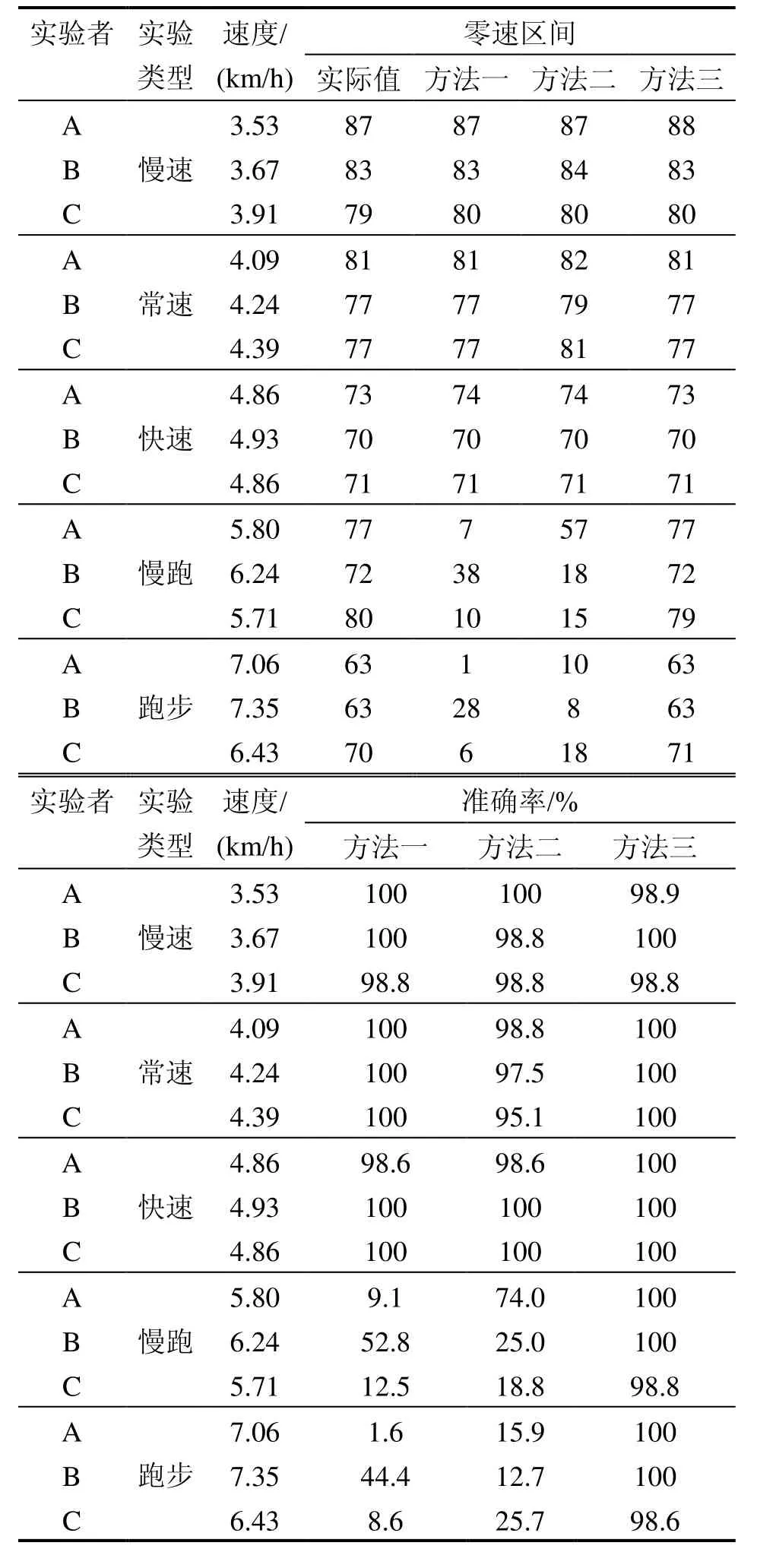
表1 零速区间检测结果Tab.1 Zero-velocity detection results
4 结 论
本文通过分析行走过程中陀螺仪输出的特性找出能够描述零速区间和非零速区间的特征量,定义了一个融合两个特征量的伪标准差使得零速区间和非零速区间的区分度增大,从而降低了检测难度,使得误判和漏判概率减小。将零速检测转化为一个二分类问题,并通过N-P准则给出了零速检测的判别规则,经过多次不同速度的行走实验数据分析,确定判断阈值,利用这个判别规则和阈值进行零速检测。
实验结果表明,本文提出的检测方法,不仅算法简单,只需要进行一次比较,不需要随着步速改变阈值,而且检测精度很高,对不同行人也有很好的适应性。

