有色噪声下的目标跟踪卡尔曼滤波新算法
林 旭,刘俊钊
(成都理工大学 地球科学学院,成都 610059)
现有的目标跟踪估计算法大多采用的是传统卡尔曼滤波(Kalman Filtering,KF)算法,而KF是一种建立在状态噪声和观测噪声均为白噪声条件下的最优估计方法。在实际的观测过程中,目标系统通常是连续的动态过程,导致噪声历元间存在时间相关性[1-3],例如,全球导航卫星系统(Global Navigation Satellite System,GNSS)的导航解决方案中就包含了误差源的影响,如大气延迟、时钟误差,它们会随时间缓慢变化。噪声的时间相关性使得KF算法的处理精度受到严重制约。对于有色噪声的处理,许多学者提出了解决方法,如状态扩增法、量测扩增法[4]、函数模型拟合法以及抗差 M-M 滤波等。其中,状态扩增法和量测扩增法是通过构造由白噪声所驱动的模型,将有色噪声作为模型参数在滤波中一并估计;函数模型拟合法在滤波解算前利用有色噪声预报值修正状态量和观测量,以控制有色噪声的影响;文献[5]采用自适应卡尔曼滤波,通过构建观测量等价权或自适应因子降低有色噪声在数据处理中的权重,从整体上控制了有色噪声,因而有着广泛的应用。这些方法皆是在传统卡尔曼滤波模型下,将有色噪声看作白噪声的简单线性函数,并结合滤波模型参与解算。但实际上,有色噪声不一定能由简单的函数模型表达,若仍将其视为白噪声的简单线性函数,上述方法的精度将难以保证。
文献[6]利用有色噪声协方差矩阵改进了卡尔曼滤波的预测状态协方差和估计状态协方差,并在协方差更新过程中减弱有色噪声对状态估值的扰动,得到较好的估计效果。文献[7]在此基础上,采用极大验后滤波公式,得到改进的状态估值方程,并利用协方差传播定律改进滤波的估计状态协方差和增益矩阵,进一步提高滤波精度。但文献[6]和文献[7]都是基于相邻历元噪声相关的假设,提出的一步相关卡尔曼滤波(One-step Correlated Kalman Filtering,OCKF)算法忽视了非相邻历元噪声间的相关性对滤波估计的影响。对此,本文首先给出了OCKF算法的基本过程,分析了有色噪声协方差的假设模型,然后从参数估计的角度,利用非相邻历元噪声间的相关性特性,建立了严密的有色噪声协方差矩阵,在线性无偏最小方差准则下,推导出多步相关卡尔曼滤波(Multi-step Correlated Kalman Filtering,MCKF)算法。
1 一步相关卡尔曼滤波算法
在KF算法基础上,OCKF算法通过计算相邻历元噪声间的协方差值,并在时间更新和测量更新过程中抵消,以减弱有色噪声对状态估计的影响[8]。
现将卡尔曼滤波的离散线性模型表示如下:

式中,Wk-1为状态噪声,Vk为观测噪声。
当机动目标跟踪系统的数据为有色噪声时,若假设相邻历元噪声之间存在相关性,不相邻的历元噪声间不相关,则有色噪声协方差矩阵D为分块三对角矩阵[6-7]。
用D1,D2,,Dn表示历元噪声的自协方差矩阵,σ1,σ2,,σn-1表示相邻历元噪声间协方差,得到:

将k-1时刻状态估值的一步预测值定义如下:

假设xk|k-1表示一步预测值与真值之差,表示状态估值与真值之差[6-7]。

将公式(4)代入公式(3),得到xk|k-1的矩阵表达式:

因此,由协方差传播定律[7],求得预测协方差:

由公式(6)可知,与KF算法相比,OCKF算法的预测协方差公式增加了对协方差改正项PXˆk-1Wk-1的计算。通过构建状态噪声与状态估值的表达式,利用协方差传播定律,得到PXˆk-1Wk-1的表达式如下:

同样,构建观测噪声与预测状态值的表达式,利用协方差传播定律,得到:

将公式(8)代入传统卡尔曼滤波公式,得到改进的估计状态协方差矩阵Pk和增益矩阵Lk如下:

2 多步相关卡尔曼滤波新算法
OCKF算法假设了相邻历元噪声间存在相关性,其协方差矩阵为分块三对角矩阵。该假设简化了滤波协方差改正项的计算过程,当历元噪声间相关性较弱时,能取得较好的滤波结果,但对于相关性较强的噪声,由于高阶项噪声间协方差数值较大且衰减缓慢,若将其忽略,滤波结果的准确性将难以保证。
为改善这一情况,本文对式(2)的协方差矩阵D加以改进。考虑到有色噪声各历元间存在相关性[9],即满足:

因此,构建改进的有色噪声协方差矩阵如下:

式中,Pi表示第k个历元噪声同间隔为i的历元噪声k间的协方差值。
首先k时刻状态估值的函数模型为[10]:

用εk表示估计状态误差,定义如下:

将式(1)(13)代入到式(14)中,计算期望值,顾及E(Wk)=0、E(Vk)=0,得到:

同时,多步相关卡尔曼滤波满足以下两条性质。
性质1状态估值k应为状态真值Xk的无偏估计[11]

将式(14)(16)代入式(15)中,得到:

顾及式(17),在式(15)的等式两边皆为0的条件下得到:

将式(1)(13)(18)代入式(14)可得估计状态误差的递推表达式:

令预测状态误差为εk|k-1,其定义为:
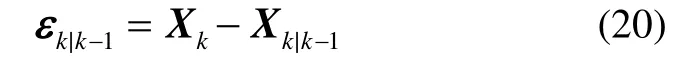
将式(3)(18)代入式(13),得到:

将式(1)(3)代入式(20),得到k-1时刻估计状态误差与预测状态误差的线性表达式:

以Pk|k-1表示k-1时刻预测状态协方差,Pk-1表示k-1时刻状态估计协方差,由协方差传播定律得到:

将式(19)在k-1时刻展开,得到由全局状态噪声与观测噪声构成的εk-1表达式。假设状态噪声与观测噪声之间互不相关[12],即cov(WkVj)=0,则存在:

将式(21)代入到式(14)得到k-1时刻预测状态误差与k时刻估计状态误差的表达式:

故k时刻的估计状态协方差为:

利用预测状态误差与观测噪声间的线性函数,得到其协方差展开式:

性质2 存在增益矩阵Lk使得状态估计的方差最小[13],故有:
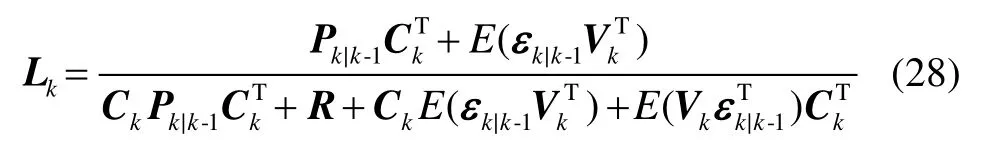
将式(28)代入式(26),整理得到:

综上,本文提出的多步相关卡尔曼滤波的公式为:

3 数值仿真实验
为验证本文所提算法的有效性,假设跟踪的目标物体在三维空间中运动,系统状态为x、y、z轴方向的位置和速度,滤波模型可描述为:

其中,

其中,ω~N(0,1),ξ~N(0,1)。
设定以下三种方案进行分析。
方案1:a=0.8,b=0.5,c=0,d=0,状态噪声为有色噪声,观测噪声为白噪声。方案2:a=0,b=0,c=0.8,d=0.5,状态噪声为白噪声,观测噪声为有色噪声。方案3:a=0.8,b=0.5,c=0.8,d=0.5,状态噪声和观测噪声皆为有色噪声。
设定数据长度为1000,目标物体保持匀速运动,分别采用KF算法、OCKF算法和本文提出的MCKF算法按上述三种方案进行200次Monte-Carlo仿真。
采用状态估计均方误差RMS作为评价指标,RMS值越小,滤波精度越高,其定义如下:

其中,N为Monte-Carlo仿真的次数,i表示第i次仿真,k表示第k个历元。图1给出了方案1下位置和速度的RMS,图2给出了方案2下位置和速度的RMS。
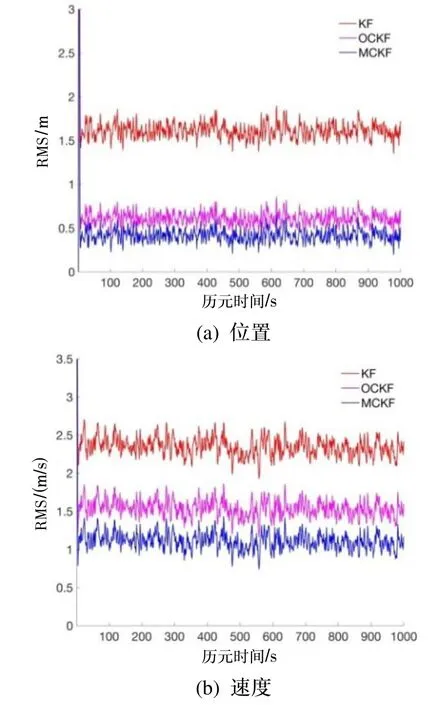
图1 3种滤波在方案1下的结果Fig.1 Results of three filters in case 1
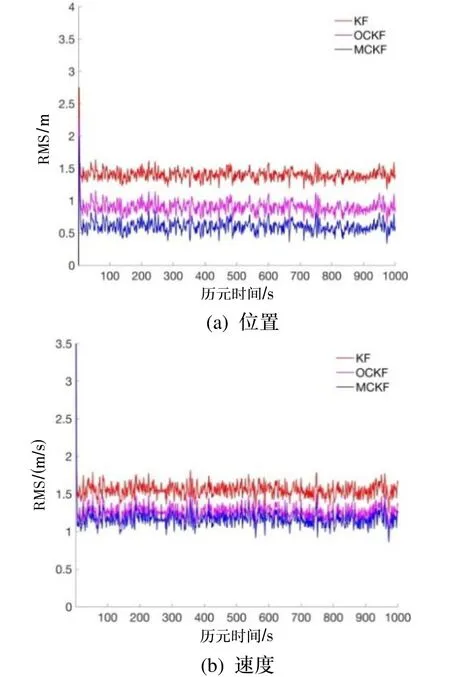
图2 3种滤波在方案2下的结果Fig.2 Results of three filters in case 2

表1 方案1下状态估计的平均RMSTab.1 Average RMS of state estimation in case 1

表2 方案2下状态估计的平均RMSTab.2 Average RMS of state estimation in case 2
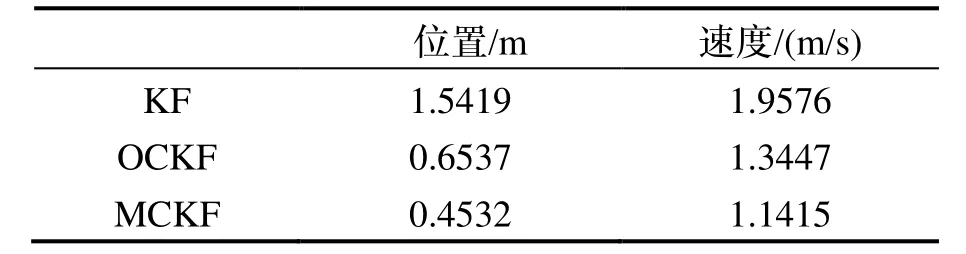
表3 方案3下状态估计的平均RMSTab.3 Average RMS of state estimation in case 3
图3给出了方案3下位置和速度的RMS。三种方案的位置和速度的平均RMS值见表1~3。需说明的是,位置和速度均是通过x、y、z轴方向的位置和速度计算所得,公式为:


图3 三种滤波在方案3下的结果Fig.3 Results of three filters in case 3
由图1和表1可见,当状态噪声为有色噪声时,KF算法得到的位置和速度的平均 RMS分别为 1.6246、2.3584,精度明显低于OCKF算法和MCKF算法。
由图2和表2可见,当观测噪声为有色噪声时,OCKF算法和MCKF算法得到的位置和速度的RMS低于KF算法,其对速度的估计精度略有提升。
由图3和表3可看出,当状态噪声和观测噪声皆为有色噪声时,OCKF算法和MCKF算法的RMS明显低于KF算法,具有较好的滤波效果。
由表1~3可得,在三种方案下,MCKF算法的状态估计RMS值均低于OCKF算法和KF算法。
实验结果表明:
① KF算法本身是基于白噪声所提出的,其利用白噪声协方差参与状态更新过程,而有色噪声则会对状态更新产生扰动,从而降低了KF算法的精度。
② 相同条件下,OCKF算法和MCKF算法对有色状态噪声的滤除效果优于有色观测噪声。
③ OCKF和MCKF算法在滤波过程中均利用了有色噪声的协方差矩阵对状态估计协方差矩阵加以改进,从而减小有色噪声的影响,而 MCKF算法因其构建的有色噪声协方差模型更加严密,故在滤波过程中拥有更高的精度。
4 结 论
当机动目标跟踪系统的数据中存在有色噪声时,传统卡尔曼滤波算法的精度和适用性会受到明显制约,难以实现高精度的数据解算。本文基于一步相关卡尔曼滤波算法的基本思想,提出了多步相关卡尔曼滤波算法,并针对有色状态噪声、有色观测噪声以及两者皆为有色噪声的三种情况进行了仿真实验,证明了多步相关卡尔曼滤波算法能够有效控制有色噪声,提高卡尔曼滤波在实际应用中的解算精度,可广泛应用于目标跟踪、导航定位、传感器融合等领域,具有一定的工程应用价值。

