基于局部可观测性分析的惯性平台连续自标定路径优化设计
王 琪,汪立新,秦伟伟,沈 强
(火箭军工程大学,西安 710025)
惯性平台连续自标定是一种“动态”标定方法。其基本原理如下:惯性平台在外力矩的作用下以角速度cω(称为加矩角速度)转动,在地球自转角速度、加矩角速度以及重力加速度的激励下,加速度计输出中包含有陀螺仪漂移、加速度计漂移、安装误差和平台对准误差等全部误差信息。以加速度计输出为观测量,以平台对准误差方程为动力学模型,采用最优滤波算法估计平台误差系数和对准误差,并用估计结果对平台模型进行补偿与调整[1]。连续自标定作为一种“动态”标定方法,在平台连续转动中的每一个采样点都相当于传统多位置自标定中的一个位置,因此连续自标定能够以很高的精度同时标定出平台的全部误差系数。在惯性平台连续自标定中,平台的转动路径会直接影响系统的模型参数,从而影响系统的可观测性。系统的可观测性是其在卡尔曼滤波中状态量估计效率的决定性因素之一,在相同的噪声条件下,系统的可观测性越好,越容易通过卡尔曼滤波估计出系统的状态量。因此通过分析可观测性来优化连续自标定的标定路径,对于简化标定流程、提高标定精度具有重要意义。
连续自标定系统是一个非线性时变系统,其可观测性分析目前仍没有一个系统有效的方法。针对线性时变系统,Goshen-Meskin和Bar-Itzhack[2-3]提出了分段定常系统(Piece-Wise Constant Systems,PWCS)方法,将时变系统看作一个分段定常系统来按时间进行分步分析,得出了其可观测性条件。Mozyrska[4]和Bartosiewicz[5]将线性时变系统的局部可观测性的概念推广到了非线性系统中。针对系统状态量的可观测性分析,奇异值分解(Singular Value Decomposition,SVD)方法在惯导系统中得到了广泛应用[6-7]。但是SVD可观测度方法存在一定的理论缺陷:不同状态对应的奇异值量纲不同,不同量纲的可观测度直接比较大小并不合理,而且该方法对于状态空间坐标系的拉伸变换不具有不变性,变换前后的可观测度分析结果可能出现不一致的情况。
本文针对惯性平台连续自标定的标定路径优化设计问题,提出了一种非线性时变系统的局部可观测性分析方法。首先推导了一种非线性定常系统的局部可观测性条件;然后根据局部可观测性条件,结合PWCS分析方法,得出了这类非线性时变系统的可观测性矩阵;对可观测性矩阵进行初等变化,利用初等变化结果定义系统状态量的相对可观测度;最后根据系统状态量相对可观测度最大原则,设计惯性平台连续自标定的标定路径。
1 非线性定常系统的局部可观测性分析
考虑如下形式的一类离散非线性定常系统:

式中,x(k)∈Rn是n维向量;z(k) ∈Rm是m维向量;A∈Rn×n和C∈Rm×n分别是n×n和m×n的常值矩阵;f:Rn→Rn是非线性有界映射。
根据式(1)有如下关系:

局部可观测性的定义如下[8]:
定义:对于非线性离散系统(1),如果状态量x(k)能够由观测量z(k)到z(k+n-1)决定,则称系统(1)为局部可观测。
式(2)中,当j=[k,k+n-1]时,有:
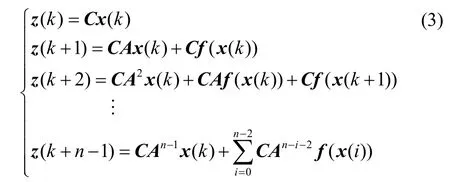
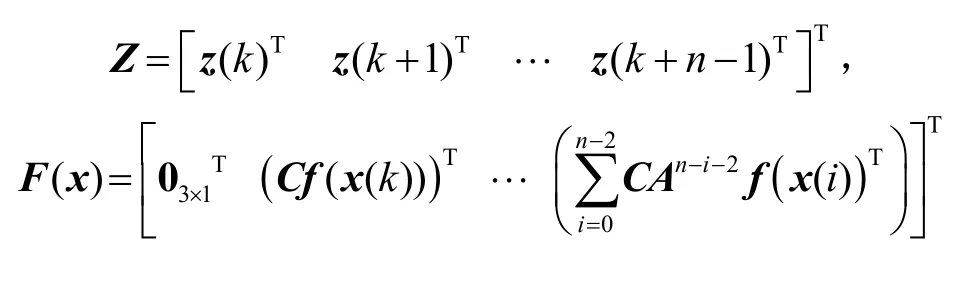
则式(3)可写为:

引理:对于式(4),如果rank(Q)=n,则式(4)在Rn中恒有解。
根据上述引理,当rank(Q)=n时,式(4)在Rn中恒有解,由于式(3)与式(4)等价,则可知x(k)能由z(k)到z(k+n-1)决定。由局部可观测性的定义可知系统(1)是局部可观测的。由此得出非线性定常系统(1)的局部可观测性条件为rank(Q)=n,称Q为系统(1)的局部可观测性矩阵。
2 非线性时变系统的可观测性分析
2.1 局部可观测性分析
考虑如下形式的一类离散非线性时变系统:

根据PWCS理论,时变系统可以近似地看作由多个分段定常系统所组成。这种近似并不会改变系统的特性,因此在分析系统的可观测性时,可以运用PWCS理论将时变系统近似为多个分段定常系统来分析[9]。
非线性时变系统(5)的分段定常系统可以表示为:

式中,j=1,2,…,r;Aj和Cj在同一个时间段里是常值矩阵,但在不同的时间段里是变化的。
对于分段定常系统(6),可以利用前面得出的非线性定常系统的局部可观测性条件来构建其全可观测性矩阵(Total Observability Matrix,TOM)如下:

式中,Δj(j=1,2,…,r)是时间段j和j+1之间的时间间隔;Qj(j=1,2,…,r)是时间段j的分段定常系统的局部可观测性矩阵。
定义提取可观测性矩阵(Stripped Observability Matrix,SOM)为s(r)=[Q1TQ2T…QrT]T,如果系统满足如下定理,则可以用SOM代替TOM以简化计算。
定理1[2]:如果NULL() ⊂ NULL(Aj)(1≤j≤r),则有NULL((r))=NULL(s(r)),并且rank((r))=rank((r))。
结合第2节得出的非线性定常系统的局部可观测性条件可知,若非线性时变系统(5)满足定理1,则系统的局部可观测性条件为rank(s(r))=n。
2.2 系统状态量可观测性分析
在惯性平台连续自标定系统中,我们更关心的是待标定的参数的可观测性,在卡尔曼滤波中,待标定的参数被看作是系统的状态量来进行估计。前面分析的局部可观测性只能表征系统整体的可观测程度,而对于具体状态量的可观测性分析则无能为力。本节对系统的SOM进行分析,利用SOM经过初等变换后的结果定义系统状态量的可观测度,从而定量表示系统状态量的可观测性。
根据PWCS理论,定义系统的可观测方程为[2]:


式中,P为一系列初等矩阵的乘积。由s(r)变换到s(r)的步骤如下:
2)如果qii<0(1≤i≤n),则将第i行乘以 -1,将qii变为正数。

对式(8)左乘P可得:
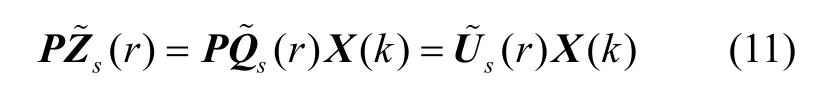

1)qii=0(1≤i≤n),且存在j1,j2,…,jk(2≤k≤n-1),使得qjk i≠ 0,则状态量xi不是独立可观测的,且与状态量xj1,xj2,…,xjk之间存在耦合;
2)qii=0(1≤i≤n),且第i列中的其他元素也等于0,则状态量xi是完全不可观测的。
如果各状态量xi(1≤i≤n)都是独立可观测的,即rank(s(r))=n,则定义与其对应的o(r)中的主对角元素qii为其相对可观测度。
此外,相对可观测度是通过对可观测矩阵进行初等变换得来,状态空间坐标系的拉伸变换并不会影响到初等变换的结果,因此避免了SVD方法中状态空间坐标系变换前后的可观测度分析结果可能出现不一致的情况。
3 惯性平台连续自标定系统的可观测性分析
惯性平台连续自标定是以姿态误差方程为状态方程,以加速度计输出为唯一的观测量,通过卡尔曼滤波来估计平台的误差系数和姿态角。通过合适的标定路径,所有的误差系数都可以被激励并且体现在加速度计输出中。由此可见标定路径对于惯性平台连续自标定的重要性,而优化标定路径的最终目的是使误差系数能够被有效的标定。在卡尔曼滤波中,误差系数的估计精度和效率与其可观测性密切相关,因此在优化标定路径前对系统的可观测性进行分析是十分必要的。
3.1 连续自标定系统状态空间方程局部线性化
首先给出惯性平台连续自标定系统的状态空间方程为[10]:

式中,φ=为平台失准角;
X=是(30× 1)的状态向量;
kg=为陀螺仪零次项和一次项误差系数;
Δ=为陀螺仪安装误差系数;
ka=为加速度计零次项和一次项误差系数;为加速度计零次项安装误差系数;ΩIp是平台相对惯性坐标系的转动角速度ωIp的反对称矩阵,ωIp由加矩角速度和地球自转角速度组成;εg为陀螺仪随机噪声;εa为加速度计随机噪声;
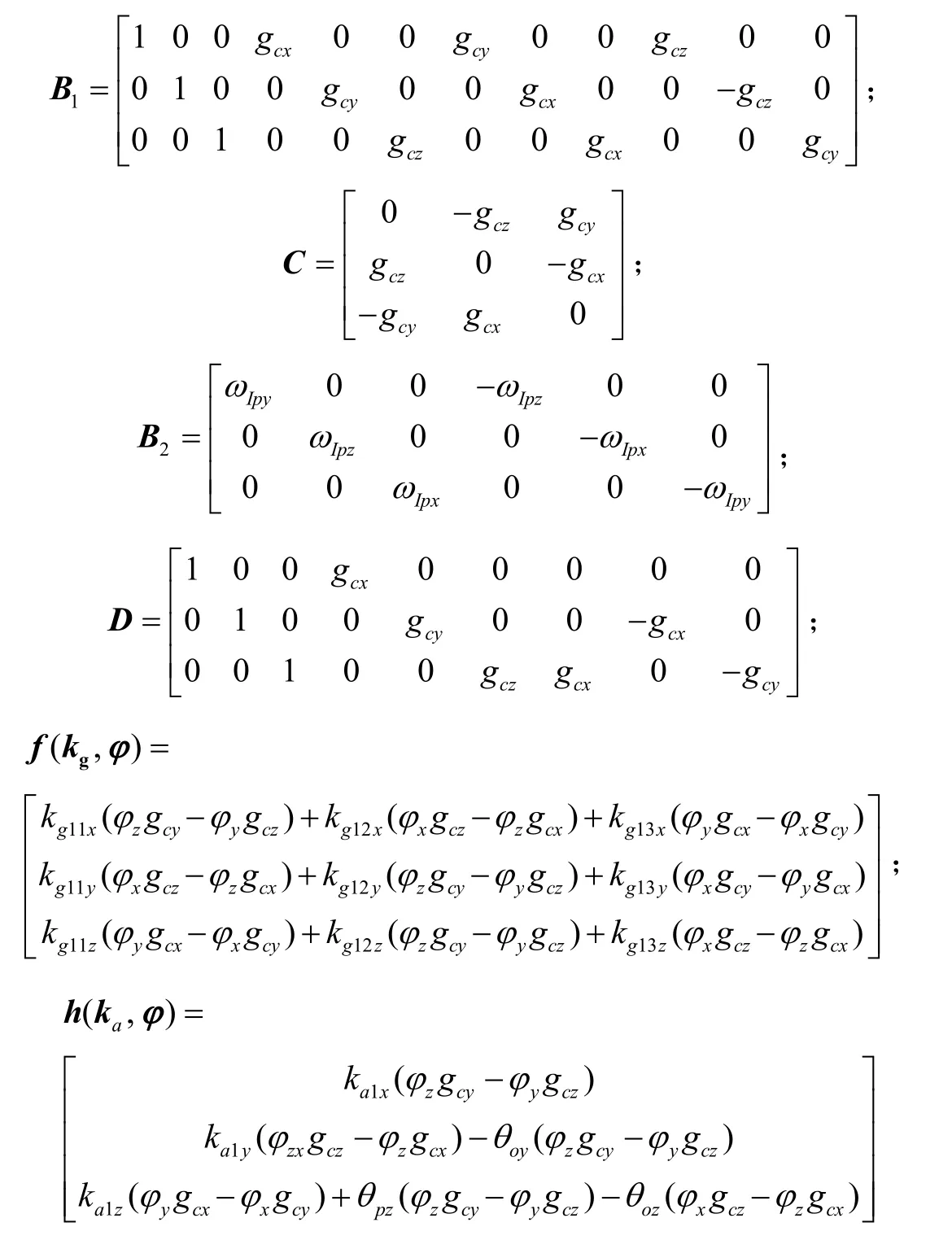
(gc为重力加速度在理想平台坐标系中的投影)。
式(13)的系统状态空间方程中,系统的状态方程和观测方程都是非线性的,这对于系统的可观测分析是不利的,因此对式(13)进行局部线性化,以简化分析过程。
在式(13)中,有:

定义Xa为系统的状态量

则有
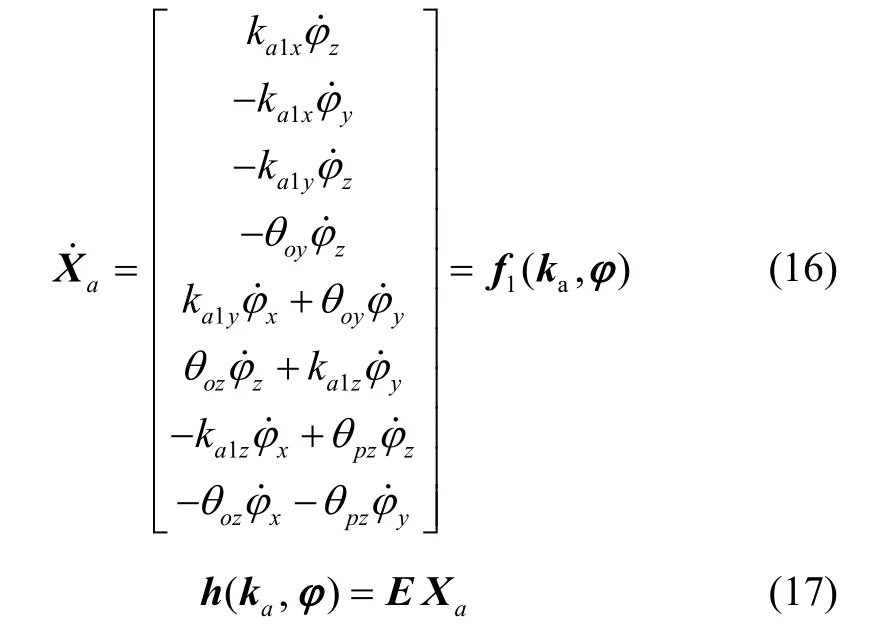
式(13)离散形式为:


H=[C018×1DE];T是系统离散时间。
在对系统的状态空间方程进行线性化和离散化后,系统的状态方程的形式与式(5)相同,则可以利用前面得出的结论分析惯性平台连续自标定系统的可观测性。
3.2 局部可观测性和相对可观测度分析
在惯性平台连续自标定中,其系数矩阵F和H随着平台转动而变化,因此是一个时变系统。根据PWCS理论,可以将其近似地看作由多个分段定常系统所组成。而平台转动时主要是改变系数矩阵F和H中的cg的分量值,考虑到在进行时间分段时不能改变系统的特性,因此设定一个时间段为平台绕一个轴转过π4角度的时间,因为在这样一个时间段内gc的各分量之间的相对关系不会改变,因而系统的特性在一个时间段内不会改变。在一个时间段内,系统的状态空间方程为:
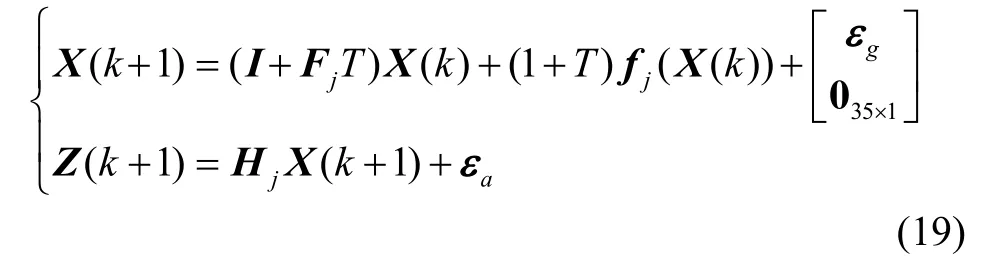
则其局部可观测性矩阵为:

惯性系统一般都满足定理1[11],因此可以用SOM矩阵代替TOM矩阵进行可观测性分析,以简化计算。设系统被分为了r个时间片段,则其SOM矩阵为:

4 自标定路径优化设计
惯性平台连续自标定中,平台框架的转动路径直接影响系统的可观测性和状态量的可观测度,从而影响误差系数的标定结果。结合自标定要求的精确性和快速性,标定路径应该满足以下几点条件[12]:
① 标定路径是连续的,以满足操作的便捷性;
② 平台框架转动路径应该尽量简单,以满足自标定的快速性;
③ 绕每个框架轴应该转动至少2π,才能激励所有的误差系数;
在实际中,大多数平台只能绕其台体轴和外环轴旋转,并且暂时不考虑加矩角速度的变化,设加矩角速度为ωc=1(°)/s。因此,为简化优化过程,设平台从导航坐标系出发,交替绕台体轴和外环轴转动,即起始角度为α0=0、γ0=0,先绕台体轴转动角度γ1,然后绕外环轴转动角度α1,再绕台体轴转动角度γ2,…,以此类推。因此在利用PWCS理论分析系统可观测性时,我们设定一个时间段为平台绕一个轴转过π4的时间,所以γ和α的取值范围为kπ4(k=1,2,…,8)。这样就可以以状态量相对可观测度最大为原则,以γ和α为变量,对自标定路径进行遍历寻优。
优化设计分为两个步骤:首先选择出γ和α取值变化时,其中rank(s(r))=30且总的转动角度最小的标定路径;然后综合比较这些路径中各个状态量的相对可观测度,相对可观测度相对最大的路径即为优化的标定路径。
在第一个步骤中得出三个满足遍历寻优条件的标定路径如表1所示。
可以看出3个路径都是分别绕台体轴和外环轴转动角度2π,只是转动的顺序有所不同。计算出3个路径下的s(r),对s(r)进行初等变换得到各个状态量的相对可观测度如表2所示。

表1 满足遍历寻优条件的标定路径Tab.1 Optimal rotation schemes in step 1

表2 各状态量的相对可观测度Tab.2 Relative observable degree of various states
根据相对可观测度的定义,表中的数据不能进行纵向对比,而只能进行横向对比。
从表中可以看出,3个标定路径下的各误差系数的相对可观测度数量级基本相同,通过综合考虑所有误差系数,确定路径1为优化标定路径。
5 仿真对比
为验证本文的标定路径优化结果,将得到的优化标定路径与文献[12]和[13]的标定路径进行仿真对比,比较误差系数的标定精度和稳定性,如表3所示。
取滤波平稳后的100个数据的相对误差的均值和标准差作为比较标定路径的指标,相对误差定义如下:

式中,x为卡尔曼滤波的滤波值,为误差系数的仿真真值。
首先设置仿真初始条件如下:
① 在连续自标定开始之前,平台处于空间稳定的工作状态,即始终跟踪当地水平面;
② 系统离散时间和滤波周期都设置为T=0.2 s;
③ 加速度计量测噪声为1×10-6m/s2,陀螺仪随机噪声为 0.0001(°)/h;

表3 标定路径比较Tab.3 Comparison of optimal rotation schemes
④ 误差系数的仿真真值在表4中给出,其中陀螺仪零次项系数单位为(°)/h,一次项系数单位为(°)/(h⋅g),加速度计零次项系数单位为m/s2,一次项系数单位为m/(s2⋅g),安装误差单位为角秒(″);
⑤ 滤波初值设置为0。
共进行100次仿真求均值,标定结果如表4所示。
图1给出了k0gy、Δsx、k0a z在一次仿真过程中的相对误差变化图,可以看出本文优化路径在标定精度和稳定性上都优于文献[12]和[13]中的标定路径。
从表4中可以看出,本文优化的标定路径对失准角、加速度计零次项误差系数、陀螺仪零次项和安装误差系数的标定精度均优于0.7%,陀螺仪一次项误差系数的标定精度在10-5级别,加速度计一次项误差系数的标定精度在10-4级别,加速度计安装误差系数标定精度能够达到10-6级别;而且标定结果比较稳定,各误差系数标定结果的标准差都小于0.01。对比可以看出,本文优化的标定路径在标定精度和稳定性上都优于文献[14]和[15]的标定路径,标定时间为12 min,能够满足快速标定的要求。证明了本文优化结果的有效性。
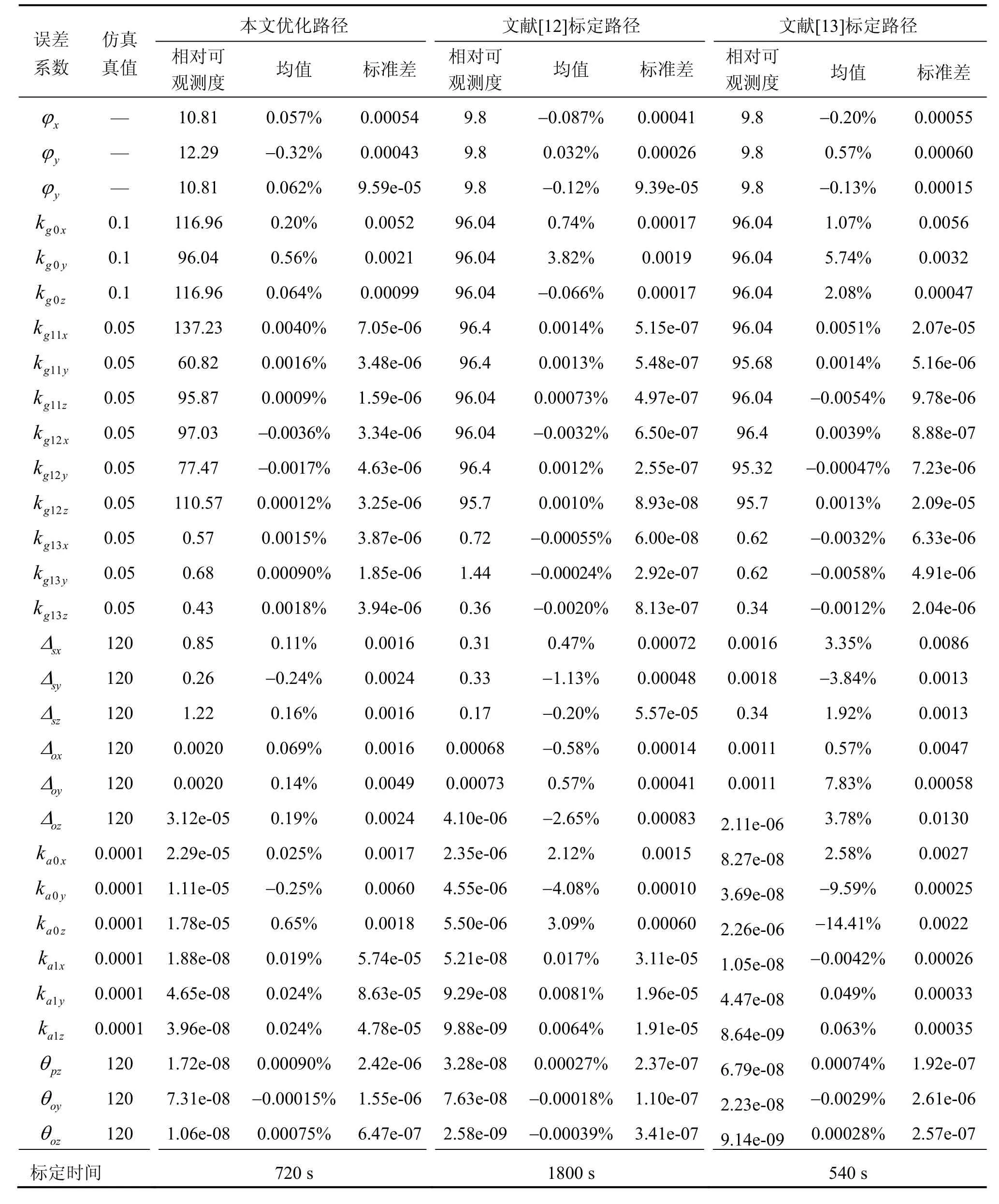
表4 相对可观测度和标定结果Tab.4 Relative observable degree and calibration results

图1 部分误差系数标定结果Fig.1 Calibration results
6 结 论
本文针对惯性平台连续自标定中的标定路径的优化问题,提出了一种基于局部可观测性和相对可观测度分析的标定路径优化设计方法。
① 推导了一类非线性定常离散系统的局部可观测性条件,基于推导出的局部可观测性矩阵,运用PWCS理论得出了这类非线性时变离散系统的局部可观测性矩阵,然后对局部可观测性矩阵进行初等变换,利用变换后得到的结果定义系统状态量的相对可观测度。
② 针对惯性平台连续自标定系统,首先对系统状态空间方程进行局部线性化和离散化,然后分析其局部可观测性和相对可观测度,并且以系统状态量相对可观测度最大为原则,对标定路径进行了优化设计。
③ 通过与已有文献的标定路径进行仿真对比,证明本文优化路径在标定精度和稳定性上都优于已有的标定路径,并且能够满足快速标定要求。仿真结果表明,在本文的仿真条件下,优化的标定路径能够以优于0.7%的相对误差标定出全部平台误差系数,在实际中具有一定应用价值。

