基于双向重投影的双目视觉里程计

张 涛，陈 浩，闫 捷，李 瑶

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；3. 北京电子工程总体研究所，北京 100854）

随着科技的进步以及人们需求的增加，移动机器人等智能机器在人类社会越来越常见，尤其是近年来，无人机等微型机器人广泛应用于搜索救援、边境侦查、工业厂房检查等[1]领域。但由于其载重的有限性以及电池的持久性限制，所携带的传感器必须具有重量轻、功耗小、高可靠性以及易配置的特点。视觉里程计（Visual Odometry,VO）以其导航高度自主、低成本及便捷等特点，在无人机等自主机器人导航领域具有重要的作用。

视觉里程计通过研究图像帧与帧间的变换关系，估计机器人相对周边环境的位置与姿态信息[2]，其主要采用两种计算方式[3]：直接法和特征点法。直接法利用图像的亮度信息，通过最小化光度误差来估计机器人的位姿信息。直接法省去了计算特征点和描述子的时间，但是直接法对单个像素没有区分度，且在光照变化时会破坏灰度值不变的假设，使算法失败。

特征点法可以分为两步：1）检测图像特征点并建立描述子，采用极线约束等方法进行特征点匹配；2）利用第一步匹配结果，由三角测量建立局部地图，解算最小化重投影误差得到位姿信息。

相比直接法，特征点法运行稳定，是视觉里程计的主流方法。

目前基于特征点法的视觉里程计存在以下问题：

1）在特征匹配阶段样本容量大、匹配准确率低，导致视觉里程计位姿估计精度下降。张云生[4]利用随机采样一致性方法（RANSAC）对匹配算法进行改进，提升了匹配精度；李小红[5]等采用PROSAC（Progressive Sample Consensus）算法来消除误匹配点，得到比RANSAC方法更好的鲁棒性和计算效率；Wu Yue等[6]采用迭代最近点法增加正确匹配点对以改进RANSAC算法，但是此方法增加了样本容量，以致算法效率降低；徐晓苏等[7]运用聚类抽样方法以降低错误匹配率；

2）视觉里程计仅通过相邻两帧进行位姿估计，必然会产生漂移误差，此外相机分辨率也会带来特征点的漂移，这些都会降低视觉里程计的精度。Bellavia F等[8]提出 SSLAM 算法，该算法通过优化关键帧的选取来缩小空间点的确定范围，提高空间点的确定精度；程传奇等[9]采用非线性优化方法并结合三维地图点以削弱累计误差；Badino H等[10]提出MFI算法，当特征点漂移到一定距离后，采用计算得到的预测特征点代替原特征点来减小漂移误差，但是该算法需要时刻计算特征点的预测值，计算量大，耗时久。

本文针对误匹配消除问题，采用在特征检测阶段选取寿命长的特征点、匹配阶段进行环形匹配以及利用优质匹配点对等方法选取优质特征点以降低RANSAC算法样本容量、提升正确匹配点对比例。针对特征点漂移与累积误差问题，提出一种基于双向重投影的位姿估计算法，解算下一帧图像中的最小化重投影误差得到初步的位姿信息，并将此位姿用于反向重投影，解算当前帧中最小化重投影误差以提升位姿估计精度。

1 基本原理

1.1 坐标系约定

在相机成像中，小孔成像模型运用最广泛。在此模型下，可以采用线性方程组来描述物体的空间坐标和图像坐标之间的关系。图1展示了模型中的坐标系关系，其中，为世界坐标系下的三维空间点，m为在图像平面的投影点，为焦距，即光心到图像平面的距离。

图1 坐标系关系图Fig.1 Coordinate system

各坐标系的定义如下：

像素坐标系——像素坐标系与图像坐标系基本一致，只有两处区别，一是将坐标原点移至图像平面的左上角顶点，二是像素是此坐标系下的基本单位。像素坐标系相对于图像坐标系的平移量为，即像素坐标系沿x轴正方向平移，沿y轴正方向平移，即可得到图像坐标系。

1.2 双目相机模型

图2(a) 双目相机的成像模型Fig.2(a) Imaging model of binocular camera

图2(b) 双目相机几何模型Fig.2(b) Geometric model of binocular camera

2 算法流程

本文以R. Mur-Artal等人的ORB-SLAM2算法[11]为基础，对其中的位姿估计部分进行改进，以期提升位姿估计精度。改进分为三个阶段：1）特征点检测阶段；2）特征点匹配与误匹配消除阶段；3）重投影阶段。

整体设计流程如图3所示，具体包括以下步骤：

Step 1：获取算法所需双目图像（本文采用KITTI数据集），在ORB-SLAM2特征点提取的基础上，记录所提取特征点的寿命，并建立对应的描述子；

Step 2：对所得的特征点进行环形匹配，选取优质匹配点对，并采用RANSAC算法进行误匹配消除；

Step 3：建立局部地图，并对空间点进行投影，解算最小重投影误差：

Step 4：更新姿态矩阵与空间点，进行反向投影，解算此时最小重投影误差，解算结果求逆，可得姿态矩阵，完成位姿估计。

图3 本文算法流程图Fig.3 Flow chart of the algorithm

3 算法实现

3.1 ORB特征点提取

特征点由关键点和描述子两部分组成。ORB算法是在2011年国际计算机视觉大会（ICCV）上提出的一种新型方法[12]。ORB算法中的关键点提取采用FAST关键点[13]检测算法。FAST是一种角点，主要检测局部像素灰度变化明显的地方，速度非常快。在以候选像素点为圆心、半径为3像素的圆周内，有N个像素点与候选像素点的亮度差别明显，则该候选像素点即为FAST关键点。设为候选像素点，且

其中，I(o)为候选特征点的灰度值，I(x)为候选点周围圆周上一点的灰度值，ω为以o 为圆心的半径为 3个像素的圆周区域，εd为符合条件的点数阈值，通常为 9、11、12，N 为符合界定条件的像素个数。如果N大于阈值，则认为o 是一个特征点。

FAST关键点检测计算简单、速度快，但FAST特征点不具有方向性和尺度信息，因此ORB通过构建图像金字塔与采用灰度质心法实现了尺度不变性和旋转不变性。所谓质心是指以图像块灰度值作为权重的中心，考虑特征点o 的一个邻域B，定义图像块的矩为

其中，p,q ∈(0,1)，r 表示图像块B 的半径，I(x,y)表示图像块(x,y)位置处的灰度值，并利用矩来定义特征点的质心：

至此，FAST关键点具有了尺度不变性和旋转不变性，大大提升了其健壮性。

在提取关键点后，ORB算法利用改进的 BRIEF特征向量来构造特征点描述子。对特征点o 的一个S×S邻域D(其中，S一般为31)，定义一个二进制测试准则τ：

其中，q(x)为点x 处的灰度值。在邻域D 选择n 个点对进行二进制测试，BRIEF描述子得到一个n 维二进制码：

由于BRIEF不具有旋转不变性，因此利用式(8)求得的特征点的方向夹角θ。假设生成特征点描述符的n 个测试点对为(xi,yi)，由式(10)可以定义一个2×n的矩阵：

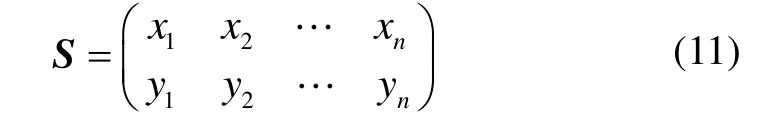
对各测试点对，利用θ形成的旋转矩阵Rθ，构造经过旋转之后的匹配点的位置Sθ：

在新的点集位置上构建二进制串描述符，此时描述子已具有旋转不变性。至此ORB特征点提取结束，下一步将进行特征点匹配与误匹配消除。

3.2 特征点匹配与误匹配消除

传统的 RANSAC方法将所有的匹配结果作为样本，样本容量大，含有误匹配较多，正确匹配比例低，效率低下。因此本文从减少误匹配数，降低样本容量方面改进RANSAC算法，具体步骤如下：

Step 1：对左右两幅图像提取ORB特征，并记录每个特征点的存活帧数，即特征点寿命。特征点的寿命越长，其可靠性越高。采取网格法将图像分成10n×10n的网格，对每个网格点内的特征点，按寿命大小进行排序，每个网格只保留前n个特征点，并使用其首次出现时的描述子。对同一个特征点使用相同的描述子可以减小漂移误差。

Step 2：对特征点进行环形匹配，如图4所示。首先采用极线约束，对当前一帧 Ii和下一帧图像 Ij的特征点进行左右图像匹配，得到左右匹配点对然后利用最近邻方法，求取最小汉明距离，对当前帧 Ii和下一帧图像Ij的特征点进行前后帧间匹配，得到匹配点对当四组匹配形成环形时，则视为有效匹配，否则匹配失败。

图4 环形匹配Fig.4 Circle match

Step 3：将所有匹配结果分为优质匹配和一般匹配，只在优质匹配中进行 RANSAC算法，缩减了样本量，提升了效率。优质匹配有两个判定标准：1）寿命长的特征点的匹配对；2）汉明距离小的匹配点对。

对同一张图片进行三种匹配实验：ORB原始匹配、经过RANSAC后的匹配、经过改进RANSAC之后的匹配。匹配结果如图5～7所示。

由图5可以看出，原始的ORB特征点最多，但是其中误匹配数量也是最多，若以此匹配结果进行位姿估计，耗时久且误差大；从图6可以看出，经过RANSAC算法去除误匹配后，匹配点对数量大大减少，误匹配数量也仅有少量残留且剩余匹配点对较集中，不利于后期位姿估计的解算；图7采用了本文的算法，可以看出正确匹配所占比例大大增加，并使正确匹配对分散开来，增强了算法的稳定性，为后续的位姿估计奠定了良好的基础。

图5 ORB原始匹配Fig.5 ORB original matching

图6 RANSAC匹配Fig.6 Matching by RANSAC

图7 改进的RANSAC匹配Fig.7 Matching by improved RANSAC

3.3 基于双向重投影的位姿估计方法

在得到匹配点对并进行误匹配消除后，需要建立局部地图并将当前帧的空间点投影到下一帧图像中，并计算投影点的最小重投影误差。但是由于特征点的漂移会导致空间点的确定带有较大误差，在计算重投影误差时误差会累积，对精度造成较大影响。因此，本文提出一种基于双向重投影的位姿估计方法，其流程如图8所示。

图8 二次重投影方法流程图Fig.8 Flow chart of the twice reprojection method

其中，K为相机内参矩阵，R为世界坐标系到相机坐标系的旋转矩阵，t为世界坐标系到相机坐标系的平移矩阵。

由于相机位姿未知以及观测点有噪声，由式(13)确定的投影点集存在误差，即重投影误差，因此构建最小二乘问题，解算最优的相机位姿，使得重投影误差D(Pi,j)最小：

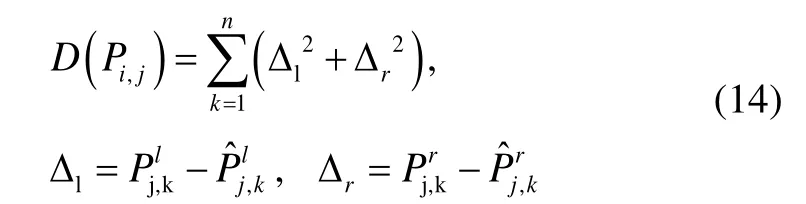
图9 重投影误差示意图Fig.9 Schematic diagram of a reprojection error

根据此时的姿态矩阵，利用式(15)更新空间点Qn=(xn,yn,zn)：

其中，Qn-1是上一次得到的空间点。

如图10所示，将更新后的空间点集 Qn投影至当前帧，重新计算重投影误差 D(Qj,i)：

图10 双向重投影示意图Fig.10 Diagram of bi-directional reprojection

4 实验结果与分析

以视觉SLAM公开数据集KITTI[14]为测试样本，KITTI数据集由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合创办，是目前国际上最大的自动驾驶场景下的计算机视觉算法评测数据集。该数据集是通过在城市地区、农村地区以及高速公路上行驶而获得的，每张图像上最多可显示15辆汽车和30名行人。

如图11所示，数据采集平台装配有2个灰度摄像机、2个彩色摄像机、一个Velodyne 64线3D激光雷达、4个光学镜头以及1个GPS导航系统，其以10 Hz的频率采样了 22个双目图像序列（8位 png灰度图像），前11个图像序列含有真实数据值，适合用来测定算法。其中相机坐标系定义为“右-下-前”，雷达坐标系定义为“前-左-上”，GPS和 IMU坐标系定义为“前-左-上”。数据集所给真值与本文所得结果均为相机坐标系下数据。

本文的实验环境为Lenovo X240笔记本电脑（酷睿i7-4600CPU，主频2.50GHZ，4G内存），以Ubuntu16.04为实验平台，选取KITTI数据集中的第1序列和第7序列。第1序列共有1104帧图像，运动时间为114 s，运行速度较快；第 7序列共有 1101帧图像，运行时间为 114 s，运动轨迹为闭环且慢速运动。分别采用ORBSLAM2方法[9]和本文算法建立视觉里程计模型，仿真实验结果如图12～15所示，图中的(x,y,z)为相机坐标系下的坐标。

图11 实验数据采集平台Fig.11 Experimental data acquisition platform

图12显示了两种算法在序列1的相对位置和姿态误差。从图12中可以看出，两种算法在各个方向上的位置误差都是越来越大，符合视觉里程计模型。与ORBSLAM2相比，本文算法解算的位置和姿态角误差都较小，累积误差明显较小。在X方向，ORB-SLAM2的最大误差大约为19 m，而本文算法的最大误差约为15 m，在Z方向（即车辆前进方向），ORB-SLAM2的最大误差大约为 25 m，而本文算法的最大误差约为20 m，精度提升了大约20%，且本文算法的稳定性优于ORB-SLAM2。

图12(a) 位置误差（序列1）Fig.12(a) Position error of sequence 1

图12(b) 姿态角误差（序列1）Fig.12(b) Attitude angle error of sequence 1

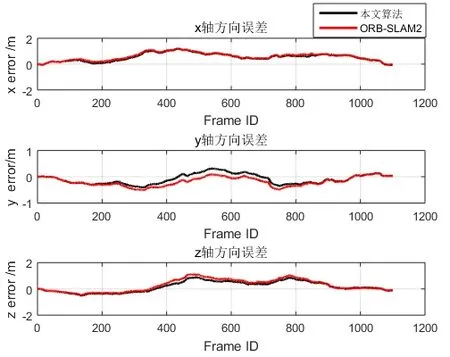
图13(a) 位置误差（序列7）Fig.13(a) Position error of sequence 7

图13(b) 姿态角误差（序列7）Fig.13(b) Attitude angle error of sequence 7

图13显示了两种算法在一个闭环运动中（序列7）的相对位置和姿态误差。从图13中可以看出，ORBSLAM2在X和Z方向的误差均在1.2 m以内，本文算法在X方向的误差在1 m以内，Z方向误差在0.9 m以内，精度提升大约20%。

图14与图15显示了本文算法与 ORB-SLAM2以及真实值的运动轨迹。图14的运动大部分近似于直线运动，误差随着运动越来越明显。由图14可以看出，本文算法与 ORB-SLAM2算法的误差都是越来越大，即包含累积误差，本文算法的误差增长幅度相对较小，整体误差约是ORB-SLAM2误差的80%。图15中运动从原点(0,0)出发，逆时针进行运动，最终回到原点。本文算法和 ORB-SLAM2都能得到较为理想的结果。与图14相比，图15所示运动因为速度较慢以及闭环检测等环节的存在，算法会对累积误差进行修正，因此图15中行程算法优化效果最好。从图14轨迹可以看出，本文算法在直线行程中的优化效果最好，定位精度提升最高 20%左右，优于ORB-SLAM2的结果。

图14(a) 解算轨迹（序列1）Fig.14(a) Trajectory of sequence 1

图14(b) 部分放大（序列1）Fig.14(b) Partial enlargement of sequence 1

图15(a) 解算轨迹（序列7）Fig.15(a) Trajectory of sequence 7

图15(b) 部分放大（序列7）Fig.15(b) Partial enlargement of sequence 7

表 1列出了两种算法在两个序列中的均方根误差（RMSE）。

表1 两种算法的均方根误差Tab.1 RMSE of the two algorithms

综上所述，实验结果可以验证本文算法位姿估计的可靠性与正确性。

5 结 论

本文针对视觉里程计中的误差累积问题，首先改进了传统的 RANSAC算法，通过特征点寿命长短、优质匹配等方法选取优质特征点以缩减 RANSAC样本容量，从而提高了 RANSAC算法的效率；然后提出一种基于双向重投影的位姿估计算法，将初次解算最小化重投影误差后的位姿估计结果应用到反向投影中，提高了位姿估计的精度；最后，利用SLAM公开数据集KITTI进行了仿真实验。

仿真结果表明，与 ORBSLAM2进行对比，本文算法在精度和稳定性上都有提升，验证了本文改进算法的正确性，说明了本文的研究具有一定的价值。

为进一步提高定位精度、抑制累积误差，下一步将考虑与其他传感器进行组合导航[15]，开展组合模式的视觉里程计算法研究。