一种变加速度的弹用双矢量空中对准方法
徐 云,洪 榛,罗志航,朱欣华,苏 岩
(1. 浙江理工大学 机械与自动控制学院,杭州 310018;2. 南京理工大学 机械工程学院,南京 210094)
初始对准是所有惯性导航系统正常工作的前提。由于制导炮弹发射时会面临高过载、高冲击、高速旋转等特殊环境,一般采取发射后系统上电的工作模式。因此,针对弹载微机械捷联惯导系统(MINS)的初始对准需要在发射后进行。目前,针对MINS的空中在线对准技术主要集中在载体在不同机动方式下各类滤波算法方面的研究[1-2],以及在此基础上改进的各类非线性滤波算法的研究[3-5]。上述滤波算法能够满足空中对准精度的要求,但载体的复杂机动方式不利于弹体的稳定飞行,并且算法的复杂度也会影响到武器系统的反应能力。区别于飞机、舰船的初始对准[6-7],弹载MINS的初始对准必须在有限的运动模式下具备快速性。
文献[8]通过比较两种坐标系下MINS传递对准的效果,指出传递对准更适用于弹载MINS的空中对准,具备精确性与快速性。文献[9]提出采用高精度的机载主惯导系统对低精度的弹载子惯导系统进行传递对准,实现了空中动基座的环境下的弹载捷联惯导的初始对准。文献[10]提出了一种基于GPS的弹载捷联惯导动基座传递对准技术,采用“速度+位置”匹配的卡尔曼滤波算法实现了弹载捷联惯导的快速对准。
上述算法均通过传递对准实现弹载MINS的空中对准。传递对准一般需采用主子惯导实现,不利于弹载测量装置、制导执行机构等的空间分配与布局。本文以实现弹体初始姿态的快速装订为目的,针对制导炮弹的飞行特点,为弹载MISN/GNSS组合导航系统设计了一种变加速度的弹用双矢量空中对准方法。
1 空中对准用双矢量
1.1 双矢量推导
设b系为前上右弹体坐标系,n系为北天东导航坐标系,ib系为初始时刻弹体惯性系,in系为初始时刻导航惯性系。t时刻的姿态矩阵可写成:
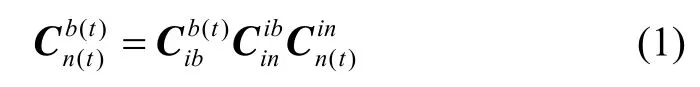

将式(1)代入式(2),并在两边同时乘以Cinn(t):

对式(3)在时间段[0,t]内积分,有:

采用分部积分的原理,对式(4)的左端进行积分得:
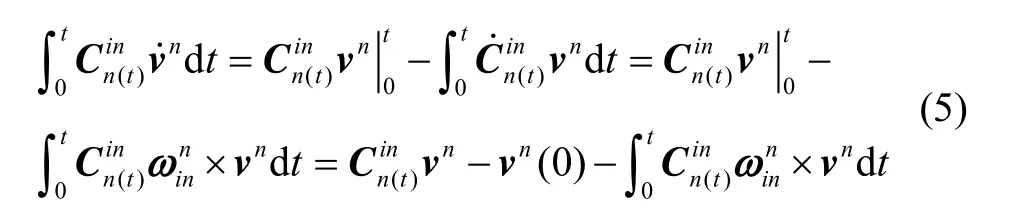
将式(5)代入式(4),根据姿态矩阵的单位正交性进行整理得:

其中,Wv和Vv分别为in系和ib系下的矢量对,如下:
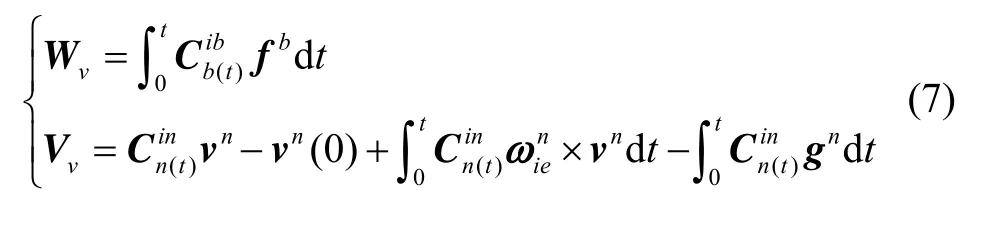
1.2 双矢量定姿算法
基于双矢量的定姿算法源于求解Wahba问题[11],常用的方法有:TRAID算法、Euler-q算法、Quest算法以及在此基础上改进的优化算法。
本文采用Request算法,构造Kk+1矩阵时采用迭代式滤波的思想,将当前时刻的观测矢量与先前时刻的观测矢量进行融合,求解Kk+1矩阵,从而实现短时间内弹用MINS初始姿态的最优估计。
图1给出了采用Request算法对当前更新周期内观测得到的双矢量W(i)和V(i)进行求解的框架图。

图1 基于Request算法的对准框架图Fig.1 Alignment algorithm frame diagram based on Request
2 对准算法误差分析
求解式(1)的全微分即可得算法的对准误差:
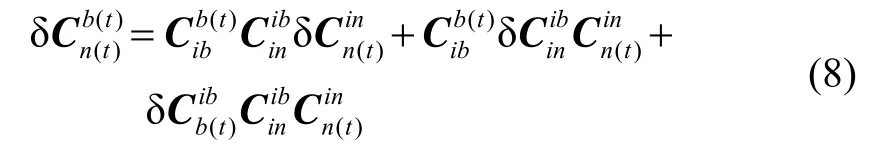

当GNSS的定位误差为10 m时,λΔ和LΔ约为0.6″,则1φ为极小角,此时可忽略误差项

根据图1的计算流程,每个周期内计算得矢量对Wv和Vv,并由此构建矩阵Kk+1,通过求解矩阵Kk+1获得姿态矩阵一般而言,t时刻的理想观测矢量Wv和参考矢量Vv确定的姿态矩阵满足实际计算时,由于测量误差、积分算法引入的误差等将会使矢量对Wv和Vv存在误差,这将导致姿态矩阵的估计存在误差
记:理想观测矢量为W=[W(1)T;W(2)T; …;W(j)T]、V=[V(1)T;V(2)T; …;V(j)T],矢量对的计算误差为δW=[δW(1)T; δW(2)T; …; δW(j)T]、δV=[δV(1)T; δV(2)T; …;δV(j)T],则最优估计得到姿态矩阵满足:
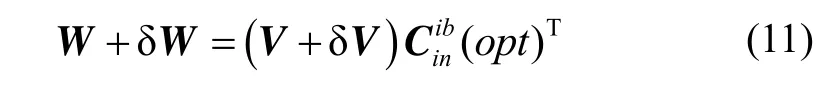
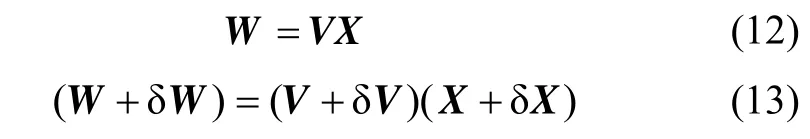
显然,式(13)为一个扰动线性方程组,对其进行整理,可得:

根据矩阵范数的相容性定理,对式(12)(13)进行处理有:
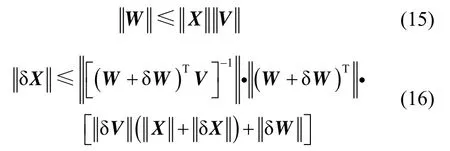
结合式(15),对式(16)的两边整理,得:
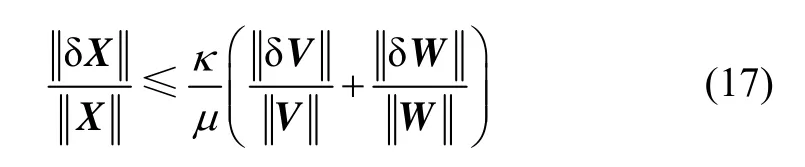
式(7)推导的矢量Vv一般可通过弹载 GNSS的测量输出准确计算获得,因此参考序列的误差 δV相对较小。将其视为0,则式(17)可写成:

式(18)表明:当κ较小时,X的相对误差较小;当κ较大时,微小的δW会导致X较大的估计误差。
为提高姿态矩阵的估计精度,需要极大化的降低κ。根据κ的表达,降低κ可通过极大化的改变W和V实现。序列W由每个时刻的W(i)构成,由式(7)可以看出,W(i)通过陀螺仪以及加速度计的测量输出计算获得,无法直接改变,因此只能设法改变序列V。根据式(7)的推导,每个时刻的V(i)可写成:

一般而言,改变矢量可通过改变矢量的方向和模值实现。由于空中飞行的弹体难以进行有目的的航向机动,这将导致改变矢量n的方向比较困难,因此只能通过选择改变矢量n的模值来实现V(i)的改变。通常改变矢量n的模值较为容易实现,如利用弹载加减速装置提供不同大小的加速度即可实现n的模值大小的变化[12-14]。
3 仿真分析
设某型制导炮弹出膛速度为800 m/s,发射位置坐标为(32°,118°,1000 m)。发射后姿态角按照如下规律变化:横滚角为γ=γ0+ωt;俯仰角为θ=θ0+θAsin(a1t+b1);航向角为ψ=ψ0+ψAsin(a2t+b2)。其中,γ0=15°,θ0=35°,ψ0=45°;自旋角速度ω=10(°)/s;俯仰角摆动幅值θA=5°,摆动频率a1=1.2πrad/s;航向角摆动幅值ψA=5°;摆动频率a2=1.8πrad/s。
设弹载MINS/GNSS组合导航系统中传感器配置如下:MINS中陀螺的测量误差主要包括零位漂移误差10(°)/h以及测量噪声10(°)/h,更新率为100 Hz;加速度计的测量误差主要包括零位偏置误差1mg以及测量噪声1 mg,更新率为100 Hz;GNSS的速度误差为0.1 m/s,位置误差为5 m,更新率为10 Hz。
3.1 变加速度与常值加速度对准分析
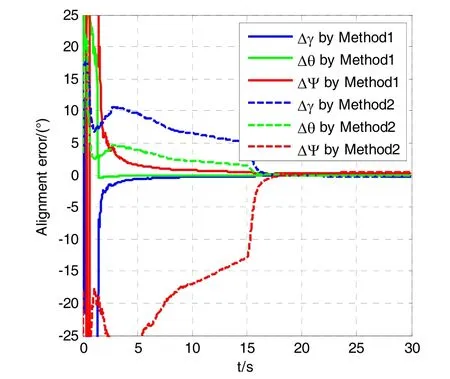
图2 两种加减速方案的空中对准误差曲线整体图Fig.2 In-flight alignment results for Method 1 and Method 2

图3 姿态角空中对准误差曲线的细节图Fig.3 Attitude errors for Method 1 and Method 2
图2和图3可以看出,基于大变加速度的空中对准方案能够在15 s内实现弹载MINS的空中快速对准,且航向角对准误差小于0.3°(1σ),俯仰角和横滚角对准误差小于 0.2°(1σ)。而基于常值加减速的空中对准方案需要在等到加减速切换后(即15 s之后)才能完成对准。这表明变加速度的对准方案有利于制导炮弹用MINS的空中快速对准。
3.2 与TRIAD算法对比
TRIAD算法为一种常用初始定姿算法,采用该方案进行初始对准所得的曲线记为 Method3。两种方法的空中对准误差曲线图如图4所示。

图4 与TRIAD算法对比的空中对准误差曲线Fig.4 Attitude errors for Method 1 and Method 3
图4可以看出,采用TRIAD算法进行对准时稳定性略差,尤其是在进行加减速切换时,对准误差较大,而本文采用的算法得到的空中对准误差曲线即Method1获得的对准误差更加稳定。
3.3 传感器标度因数误差影响分析
添加陀螺仪、加速度计的标度因数误差100×10-6、200×10-6、300×10-6进行仿真对比,结果如图5所示。
由图5可以看出,随着标度因数误差的增大,对准误差也随之增大,且航向角的对准误差最大。
上述仿真对比可以看出,本文提出的基于变加速度的对准方案可较快的实现弹体的空中对准,但传感器的标度因数误差是影响对准结果的一个重要因素。在实际应用时应选择合适的传感器,根据制导炮弹全弹道飞行特征选择合适的变加速度方案,从而实现制导炮弹用MINS飞行中的快速在线对准。
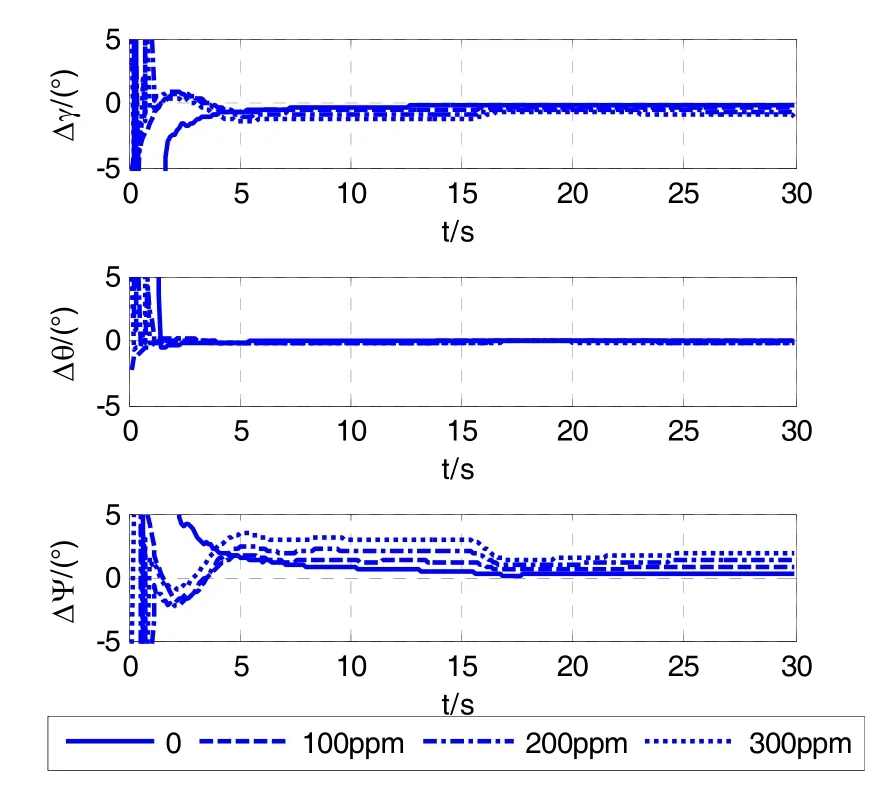
图5 不同标度因数误差所得的空中对准曲线Fig.5 In-flight alignment results for different scale factor errors
4 结 论
本文针对制导炮弹空中飞行时间较短以及为保证弹体稳定飞行,难以实现有目的的航向机动,提出了一种变加减速的弹用双矢量空中对准算法。根据速度微分方程推导了空中对准用的双矢量,并利用双矢量定姿的原理进行初始姿态的估计。通过分析对准算法的误差,提出了一种变加速度的空中对准方案实现弹载MINS初始姿态的最优估计。数值仿真对提出的变加减速的弹用双矢量空中对准进行了分析。结果表明,以指数函数作为变加减速的对准方案可在短时间内较快地实现弹载MINS初始姿态的估计。本文提出的一种变加速度的弹用双矢量空中对准算法的对准精度和对准时间均能满足弹载MINS在线对准的需求。

