基于傅里叶变换的时变参数回归模型：估计、设定检验和实证应用

杨利雄，李庆男(.兰州大学 管理学院 甘肃 兰州 730000； .“中山大学” 经济研究所 台湾 高雄 806)

一、引 言

在过去几十年里，已有的计量模型和经济管理类实证研究多基于线性回归模型[1]，且线性回归模型还被施加了诸多严格的假设，如参数为常数。同时，学者已认识到非线性在经济现象中的普遍存在性[2-3]，但Granger证明，任何非线性模型都能被一个时变参数的线性模型很好地近似[1]。从而线性模型因其简洁性成为诸多研究中的首选。

然而，对时变参数的线性模型研究还很不够。模型参数的时变性会影响模型的拟合优度及造成预测的失败[3]。现有的考虑模型系数时变性特征的方法多基于卡尔曼滤波[4]505-506，然而其不仅需要估计观测模型的系数，还需要估计状态方程的协方差矩阵，太多的参数估计不仅造成效率的损失，还损失了简洁性进而影响了其在实际问题中的应用。

傅里叶变换通过三角函数序列能以任意的精度逼近绝对可积的函数。同时Becker等证明低频的傅里叶函数就能很好地解决很多常见的时变特征[2]。Enders 和 Lee等使用傅里叶变换处理单位根检验中的时变参数问题[5-6]。杨利雄和张春丽使用傅里叶变换处理协整模型中的结构突变，发现能较好地捕捉结构突变从而促进参数估计的效率[7]。

本文基于傅里叶变换和简单最小二乘回归模型框架建立了一个简单易用的时变参数线性回归模型，并给出了其估计和模型的设定检验方法。通过使用傅里叶变换近似时变参数，从而得到一个包含三角函数项、三角函数与自变量交叉项的回归模型作为辅助回归，并证明模型的参数估计是收敛于真实值的，进一步得到的时变参数的估计也是收敛于真实值的。另一方面，当模型参数本身无时变性时，使用时变参数模型方法会估计多余的参数，而估计多余的参数会损失效率，因而本文建立了模型设定检验以帮助选择是否使用时变参数模型。然后，使用蒙特卡洛模拟方法，考察基于傅里叶变换的时变参数模型处理常见的时变参数类型的效果，发现新的时变参数模型能很好地处理连续的、随机的和跳跃的时变参数线性模型。新方法的一个主要优点是模型的简洁性和应用的便捷性。

最后，将新建立的时变参数线性模型应用于研究中美两国股市的联动性，发现考虑模型参数的时变性特征后能显著提升模型的拟合优度；同时，时变参数模型能得到更为丰富的联动特征，帮助理解联动现象或帮助投资者在全球分散风险，而忽略模型参数的时变性可能得到错误结论。

二、时变参数回归模型理论：估计和设定检验

本节建立基于傅里叶变换的时变参数线性回归模型，并给出其参数估计方法、估计的收敛性特征，同时给出模型的设定检验。

(一)基于傅里叶变换的时变参数模型及其估计

考虑如下时变参数的模型：

yt=αt+βtxt+εt

(1)

假设yt和xt是平稳变量且模型(1)满足经典回归所需的条件，其中xt和yt可以是向量的形式，αt和βt是时变参数。

近年来，学界已经认识到使用傅里叶变换近似时变性特征(如非线性和结构突变)的优点[2]。傅里叶函数近似时变性的方法不需要假设时变性的先验知识，因而可避免时变参数类型误设问题，另外傅里叶函数也可以处理非线性趋势，这使得该方法十分具有竞争力[8]。

只要αt和βt是时间t的绝对可积函数，则傅里叶变换可以以任意的精度近似αt,βt：

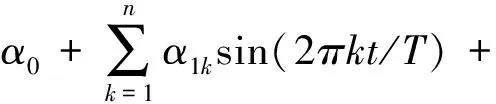
(2)

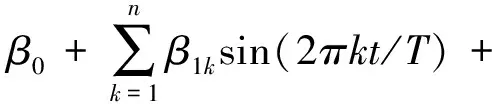
(3)

其中，n代表傅里叶近似中包含的频率的个数，k表示某一特定的频率，T是样本数。

单频的傅里叶函数就能很好地近似常见的时变性结构[2]，为了模型推导的方便考虑如下单频的时变参数近似：

αt≅α0+α11sin(2πkt/T)+α21cos(2πkt/T)

(4)

βt≅β0+β11sin(2πkt/T)+β21cos(2πkt/T)

(5)

将式(4)和式(5)代入时变参数模型(1)可得如下辅助回归模型：

yt=α0+α11sin(2πkt/T)+α21cos(2πkt/T)+

β0xt+β11xtsin(2πkt/T)+

β21xtcos(2πkt/T)+εt

(6)

对于频率参数k的选择，参照Becker等人的做法[2]，从1,2,3,4,5中选择，可使用最小化残差平方和的方法，分别选择k=1,2,3,4,5，计算式(6)最小二乘估计的残差平方和SSR(k)，选择能使SSR(k)最小的参数k即可。

因为xtsin(2πkt/T)和xtcos(2πkt/T)不再严格满足弱平稳的定义，因而传统的最小二乘回归的理论(如系数的收敛性特征等)可能不再成立。因而本文先推导辅助回归模型的系数估计的收敛性。

定理1 模型(6)中参数的最小二乘估计是收敛的，其收敛速度均为O(T-1/2)。

证明：为了方便推导，先定义如下向量：

τ=[1，2，…，T]′，Υ1=[sin(2πk1/T)

sin(2πk2/T)，…，sin(2πkT/T)]

Υ2=[cos(2πk1/T)，cos(2πk2/T)

…，cos(2πkT/T)]

Υ3=[x1sin(2πk1/T)，x2sin(2πk2/T)

…，xTsin(2πkT/T)]

Υ4=[x1cos(2πk1/T)，x2cos(2πk2/T)

…，xTcos(2πkT/T)]

G=[τ，Υ1，Υ2，Υ3，Υ4]

θ=[α0，α11，α21，β0，β11，β21]′

(7)

根据Hamilton和Becker等人给出的变量有界性特征[2][4]505-506，有：

定理2 基于模型(6)中参数的最小二乘估计，构造如下估计量：

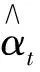
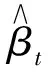
(二)模型设定检验

估计不必要的参数会带来效率损失，因而当模型不含时变性时，考虑时变性是不合意的。因此，在使用时变参数回归模型之前，有必要检验系数时变性特征的存在性。

如果模型(1)中系数不含时变性，则模型(6)中α11=α21=β11=β21=0。这一特征可以用来做模型的设定检验。即为了决定是否应该考虑结构突变特征，可以检验如下原假设：

H0∶α11=α21=β11=β21=0

(8)

设SSR0为回归模型yt=α0+β0xt+εt的残差平方和；SSR1为回归模型(6)的残差平方和。则下列F统计量可以用来检验原假设：

(9)

上述F统计量服从自由度为4和T-6的F分布。F统计量拒绝上述原假设是模型(1)的系数不含时变性的信号。

使用传统的F检验做设定检验，虽然理论简单且易于使用，但其小样本性质差*误差项服从独立同分布时，传统F检验具有良好的有限样本表现。[9]。Kiefer等提出通过对最小二乘回归的残差进行转换[10]，从而构造稳健统计量的方法，其方法被证明具有优良的小样本性质[11]。因此，本文通过转换最小二乘回归的残差构造稳健的设定检验。

为了方便构造统计量，先将模型(6)的最小二乘估计表示为如下向量形式：

(10)

其中，xt=[1，sin(2πkt/T)，cos(2πkt/T)，xt，xtsin(2πkt/T)，xtcos(2πkt/T)]′，

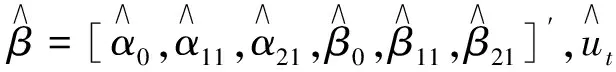
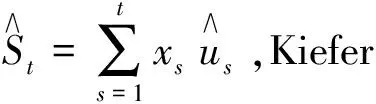
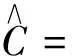
[W4(r)-rW4(1)]′dr]Ω′1/2

其中，Ω为Xtut的协方差矩阵，W4(r)为4维的相互独立的标准维纳过程。

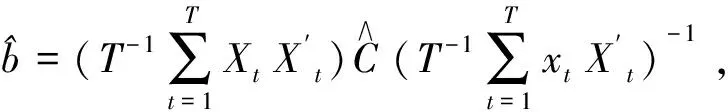
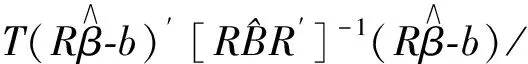
(11)

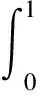
式(11)中的极限分布不是标准的F分布，但其极限分布不依赖于冗余参数。通过使用正态分布的随机数叠加近似维纳过程，使用随机模拟给出其临界值。该检验1%、5%和10%的临界值分别为108.22、65.35和48.71。

三、蒙特卡洛模拟

(一)基于傅里叶变换的时变参数模型的表现

讨论了基于傅里叶变换的时变参数回归模型的设定和系数的收敛速度，本节使用蒙特卡洛模拟研究前文建立的基于傅里叶变换的时变参数回归理论处理时变参数问题的效果。使用模拟的数据对比回归模型yt=α+βxt+et和回归模型(6)在拟合随机模拟数据时的拟合优度。

1.数据生成过程

考虑三种常见的时变参数数据生成过程：连续的、随机的、跳跃的时变参数模型。

1)连续的时变参数

考虑如下的数据生成过程：

yt=αt+βtxt+εt

(12)

αt≅α0+α11sin(2πkt/T)+α21cos(2πkt/T)

(13)

βt≅β0+β11sin(2πkt/T)+β21cos(2πkt/T)

(14)

其中εt～i.i.d.N(0，1)，t=1，2，…，T。模拟时选取如下参数：k=1，α0=β0=0，α11=α21=β11=β21=1，样本T分别选取100和1 000。

2)随机的时变参数

考虑如下系数随机的数据生成过程：

yt=αt+βtxt+εt

(15)

αt=αt-1+ν1t

(16)

βt=βt-1+ν2t

(17)

其中，εt，ν1t，ν2t～i.i.d.N(0，1)且相互独立。

3)跳跃的时变参数

考虑如下具有跳跃特征的时变参数数据生成过程：

yt=αt+βtxt+εt

(18)

(19)

(20)

其中εt～i.i.d.N(0，1)且α1≠α2，β1≠β2。模拟时选取参数α1=β1=1，α2=β2=2。

2.蒙特卡洛模拟结果分析

选取样本容量T=1 000，使用数据生成过程式(12)～(14)生成样本，并使用简单的回归模型yt=α+βxt+et时，发现估计的系数均在10%的显著性水平下不显著，且拟合优度R2仅为0.002 2；样本T=100时且使用简单回归模型yt=α+βxt+et时有类似的结论，即估计的系数均在10%的显著性水平下不显著，且拟合优度R2仅为0.016 8。然而，在样本T=1 000和100时使用模型(6)得到的拟合优度R2分别为0.52和0.44。进一步地，使用前文式(9)给出的F分布做模型的设定检验，F统计量在1%的显著性水平下拒绝了原假设，因而应该使用时变参数模型。

用随机时变参数模型(15-17)和跳跃时变参数模型(18-20)生成样本，使用模型(6)均能显著地提高模型的拟合优度，且据模型设定检验(9)中的F统计量都能在1%的显著性水平下拒绝原假设，因而F检验的证据支持时变参数模型。

综上，模拟表明：本文的基于傅里叶变换的时变参数模型对常见的时变参数数据生成过程都有较好的处理效果。

(二)模型设定检验的有限样本表现

为了对比前文模型设定检验的表现，从而更加直观地理解其优良性，本节使用蒙特卡洛模拟考察前文模型设定检验的小样本性质。

在考虑模型设定检验的检验水平时，选取原假设下的数据生成过程yt=α0+β0xt+et，其中选取参数α0=β0=1；在考虑检验功效时，选取备择假设下数据生成过程：yt=αt+βtxt+et，其中αt，βt分别由式(13)和式(14)所示，其中的参数选择k=1，α0=β0=1，α11=α21=β11=β21=0.1。另外设置et=ρet-1+ξt，ξt～i.i.d.N(0，1)，选取参数ρ=0.1，0.25，0.5，0.75，0.9。

表1给出了在5%的显著性水平下，使用传统的F检验和基于转换最小二乘残差建立的稳健检验的有限样本表现。随机模拟使用GAUSS 9.0编程完成，每次模拟重复10 000次。

模拟的结果表明：随着回归模型误差项自相关程度的增强，传统F检验以非常高的频率错误地拒绝原假设，即存在严重的检验水平扭曲(size distortion)问题，且这种检验水平的扭曲随样本的增加并无明显改善；与之对比，F*统计量具有无检验水平扭曲的特点。另一方面，从检验功效的角度来看，F*的检验功效略低于传统的F检验，但这种检验功效的损失并不严重。

给定常用计量软件中的统计量多为传统F检验，模拟结果对传统F检验的使用给予了警示。为了得到更为准确的结果，F*统计量应该是一个更好的选择，尤其是在误差项存在高度自相关的情况下。

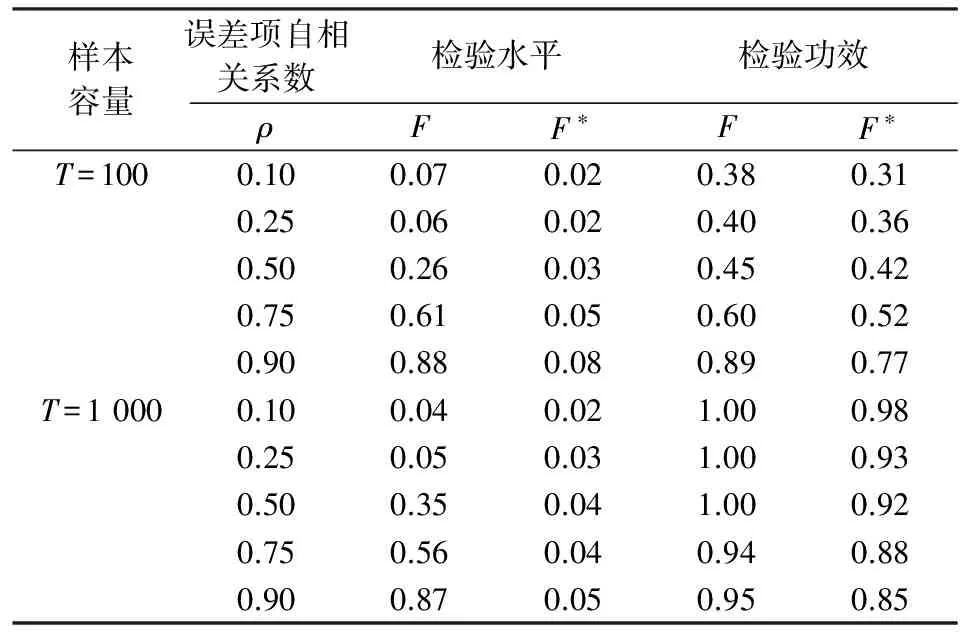
表1 设定检验F和F*的有限样本性质

注：检验水平为原假设成立时5%的显著性水平下的拒绝率；检验功效为备择假设成立时5%的显著性水平下的拒绝率。

四、实证应用

股票市场之间的联动关系是投资者在全球分散风险的重要依据，当股票市场之间存在密切的联动关系时，投资者在全球分散投资的收益是非常有限的[12]，而市场之间的联动关系具有时变性已经成为共识。因而股票市场间时变性关系的考察是调整投资组合的主要依据。

随着中国的迅速崛起，中国股票市场对全球其他市场的影响力越来越强[13]，因而研究中国与美国股票市场的联动关系对投资者在国际市场间配置资产具有重要意义。本文使用前文的时变参数线性模型考虑时变参数对研究中美两国股市联动的重要性。

基于协整理论研究股市联动的文献中一般考虑如下的回归模型：

Sch，t=α+βSus，t+δt+et

(21)

考虑系数的时变性特征，可以建立如下时变参数回归模型：

Sch，t=αt+βtSus，t+δtt+et

(22)

其中，at，βt如式(4)和式(5)所示，Sch，t，Sus，t分别代表中国的上证综指和美国的道琼斯指数。本文选取的时间段为1990年12月19日到2014年12月31日。

首先使用式(9)中的模型设定性检验判断时变参数的存在性，从而以便在模型(21)和(22)之间做出选择。基于模型(21)的残差平方和SSR0=1.95×109，基于模型(22)的残差平方和SSR1=1.22×109，从而容易计算出式(9)中F统计量的值：F=301。基于式(11)的F*统计量为：F*=94.58。两者均能在5%的显著性水平下拒绝参数为常数的假设。因而应该选择考虑时变参数的模型(22)。所以考虑如下模型：

Sch，t=α+α11sin(2πkt)+α21cos(2πkt)+

βSus，t+β11sin(2πkt)Sus，t+

β21cos(2πkt)Sus，t+δt+δ11tsin(2πkt)+

δ21tcos(2πkt)+et

(23)

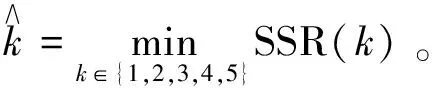
使用最小二乘法估计回归方程(23)得到：

Sch=5 222.73-1 327.42sin(2πkt)-

4 521.26cos(2πkt)+0.16Sus-

0.33Sussin(2πkt)-0.13Sus，tcos(2πkt)-

2.04t+0.49tsin(2πkt)+

2.33tcos(2πkt)+et

(24)

式(24)中所有系数在1%的显著性水平下显著，其R2为0.772，相对于基于模型(21)得到的R2=0.634有很大的提高。

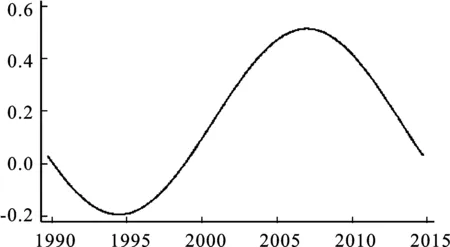
因而，可以得到时变参数模型估计：

(25)

其中

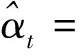
年限

另一类文献，注重基于股市收益率分析市场间的联动关系，如基于GARCH族模型或基于收益率之间回归的研究[14]。本文考虑基于回归模型的市场间联动。若不考虑模型参数的时变性，则建立如下模型：

rch，t=a+βrus，t+et

(26)

考虑到回归模型参数的时变性特征，则应当建立如下模型：

rch，t=at+βtrus，t+et

(27)

其中at，βt如(4)和(5)所示，rch，t，rus，t分别为中国股市和美国股市的收益率。

为了在模型(26)和(27)之间做选择，先计算出式(9)中F统计量的值：F=522.28。基于式(11)的F*统计量为：F*=114.21。均在1%的显著性水平下拒绝了参数为常数的假设，因而模型设定检验支持使用模型(27)。

本文基于简单的时变参数模型得到的结论与文献基于复杂模型得到的结论一致。例如：在协整回归框架下，Zhang和Li发现中国股市与美国股市之间的联动关系存在时变性，且在金融危机时期联动性显著增强[15]；Chou和Cai使用双平滑转移条件相关-条件自相关模型(Double Smooth Transition Conditional Correlation-conditional Autoregressive Range model)考察股市联动问题，发现中国股市与美国股市之间的联动关系存在显著的时变性特征[16]。因此，如果不考虑参数的时变性特征，基于简单的线性回归模型可能得到错误结果；如果考虑参数的时变性，本文的时变参数回归模型可以很好地处理实证问题。

五、结 论

过去几十年里，线性模型在计量经济学和实证经济管理类文献中被普遍研究和使用。虽然非线性被发现普遍存在于经济现象中，由于非线性模型往往能被线性模型很好地近似，因而线性模型在实际应用中依然十分受欢迎。然而，含时变参数的线性模型还很少被研究，而模型参数的时变性是模型拟合优度与预测的重要障碍。

本文基于傅里叶变换建立了一个考虑回归模型系数时变性特征的方法，并给出了模型的估计方法和设定检验。使用蒙特卡洛模拟表明：新建立的方法能很好地处理各种常见的时变参数类型，如连续的时变参数、随机的时变参数和跳跃的时变参数；传统的F检验存在严重的检验水平扭曲，F*统计量无检验水平扭曲的问题且易于计算。本文的方法具有模型的简洁性和应用的便捷性特征。

最后，本文将该方法应用于研究中美两国的股市联动特征分析。发现不管是基于股票指数序列还是基于收益率序列，考虑模型参数的时变性特征都能显著提升模型的拟合优度，同时能提供更为丰富的联动特征帮助投资者在全球范围分散投资。反之，若不考虑参数的时变性，则可能得到错误结论。对比研究本文的时变参数线性模型与基于卡尔曼滤波的时变参数模型的优劣及其各自发挥优势的条件，是未来值得研究的课题。

[1] Granger C W.Non-linear Models：Where do We Go Next-Time Varying Parameter Models?[J].Studies in Nonlinear Dynamics & Econometrics，2008，12(3).

[2] Beckers R，Enders W， Lee J.A Stationary Test in the Presence of an Unknown Number of Smooth Breaks [J].Journal of time series Analysis，2006，27(1).

[3] D' Agostino A，Gambetti L，Giannone D.Macroeconomic Forecasting and Structural change[J].Journal of Applied Econometrics，2013，28(1).

[4] Hamilton J D.Time Series Analysis[M].Princeton：Princeton university press，1994.

[5] Enders W，Lee J.The Flexible Fourier form and Dickey-Fuller Type Unit Root Tests [J].Economics Letters，2012，117(1).

[6] Lee C，Wu J L，Yang L.A Simple Panel Unit-Root Test with Smooth Breaks in the Presence of a Multifactor Error Structure[J].Oxford Bulletin of Economics & Statistics，2015，78(3).

[7] 杨利雄，张春丽.基于傅里叶变换的含确定性趋势结构突变的协整回归模型和不等方差检验[J].统计研究，2014(11).

[8] 杨利雄，张春丽，李庆男.含非线性的平稳变量之间的虚假回归研究[J].统计与信息论坛，2016(1).

[9] Sun Y.Let’s Fix It：Fixed-b Asymptotics Versus Small-b Asymptotics in Heteroskedasticity and Autocorrelation Robust Inference[J].Journal of Econometrics，2014，178(2).

[10] Kiefer N M，Vogelsang T J.Bunzel H.Simple Robust Testing of Regression Hypotheses[J].Econometrica，2000，68(3).

[11] Yang L，Lee C，Shie F.How Close a Relationship Does a Capital Market Have with Other Such Markets? A Re-Examination Based on the Equal Variance Test [J].Pacific-Basin Finance Journal，2014，26(3).

[12] Diamandis P F.International Stock Market Iinkages：Evidence from Latin America[J].Global Finance Journal，2009，20(1).

[13] 杨利雄，李庆男.中国股市与国际股市联动关系的“密切”程度[J].山西财经大学学报，2013(3).

[14] 蔡义杰，周雨田，李丹.次贷危机下美国和全球股市之联动[J].国际金融研究，2009(9).

[15] Zhang B，Li X M.Has There Been any Change in the Comovement Between the Chinese and US Stock Markets?[J].International Review of Economics & Finance，2014，29(1).

[16] Chou R Y，Cai Y.Range-based Multivariate Volatility Model with Double Smooth Transition in Conditional Correlation[J].Global Finance Journal，2009，20(2).