不同星历的GAMIT高精度基线解算

王树东，万 军，2

(1.建设综合勘察研究设计院有限公司，北京 100007；2.中国测绘科学研究院，北京 100830)

0 引言

全球定位系统(global positioning system，GPS)测量数据处理是研究全球卫星导航系统(global navigation satellite system，GNSS)定位技术的一项重要内容，其中尤为重要的是GPS基线解算。目前，高精度GPS数据处理软件国际上比较知名的是GAMIT数据处理软件，采用双差观测量解算模式，通过最小二乘算法进行参数估计，其优点是可以完全消除卫星钟差与接收机钟差产生的影响，同时也能大幅度减弱大气折射误差、轨道误差等的影响。GAMIT基线解算过程中通常要求精密的轨道信息文件作为位置基准，但是在实际工作中由于最终精密星历的播发是延后的，所以有时在一些需要实时进行解算基线的工程中，不能满足GAMIT基线解算的要求[1-5]。

本文通过分析星历精度对于定位精度的影响，探讨基于不同的星历进行GAMIT基线解算与平差计算的方法。

1 星历误差

1.1 星历类型

按照精度划分，GPS卫星星历可以分为精密星历和广播星历。国际GNSS服务组织(International GNSS Service，IGS)负责提供各种导航定位系统的星历，由7个IGS处理分析中心的结果进行加权平均之后得到，主要分为最终星历、快速卫星历和超快速星历3种。广播星历较精密星历的精度稍差，目前主要用于导航定位、低等级或短基线的工程测量[6-8]。

星历的更新时刻为世界协调时(coordinated universal time，UTC)。各种星历的具体情况如表1所示。

表1 星历类型

1.2 星历误差对定位精度的影响

卫星星历误差指卫星星历给出的卫星位置与卫星实际位置之差。卫星在空中运行时，会受到很多力的影响，如天体引力摄动、太阳辐射压力、卫星钟差等。经过理论的分析与实验研究，卫星星历误差对相对定位的影响结果为

(1)

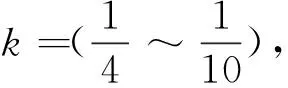
表2 不同星历的相对基线误差

2 计算流程

2.1 基线解算原理

假设在2点同步观测s、k卫星，可以组成2个单差观测方程为：

(2)

(3)

式中：A、B表示2台接收机；s、k表示卫星；f为相位频率；τ为波长；ρAB为t时刻测站到卫星的几何距离；δAB为接收机钟差；NAB为t时刻的相位整周未知数；ΔAB为大气误差。

仅考虑频率相同的情况，即τs、τk相同时用τ表示，对式(2)及式(3)求差化简可得

(4)

由式(4)可见通过双差观测方程消除了卫星钟差与接收机钟差。对于短距离基线来说，大气误差影响较小，可忽略不计。此时的未知参数为2测站的相对矢量和整周模糊度[9-10]。

2.2 解算策略设置

本文中的解算软件为GAMIT 10.5，其需要在UNIX或LINUX系统中运行，同时需要GCC编译器的支持。软件的具体安装步骤可参考相关文献，本文不再对软件的安装进行详细讲述。

比特币交易是相互关联的输入输出交易事务，使用未经使用的交易的输出（UTXO）作为输入，并生成新的输出。同一笔交易可以有多个输入和多个输出，具体交易格式如表1所示。

GAMIT数据处理主要的解算策略设置，采用轨道松弛模式；LC_AUTCLN解算类型；光压模型采用BERNE；对流层天顶距延迟参数采取2 h估计1个，采用GMF映射函数；海潮改正模型采用FES2004；卫星截止高度角设置为10°。

2.3 解算流程

2.3.1 基线解算处理流程

1)GAMIT的参数设置。采用RELAX解模式，解的数据类型为LC-AUTCLN，卫星截止高度角为10°，对流层延迟每2 h设置1个，对基准站N、E、U方向的约束都为5 cm。

2)GAMIT数据解算分步进行处理，编制调用GAMIT有关模块的命令。通过创建一个年积日文件夹，将观测文件、广播星历文件以及tables中的文件复制到年积日的文件夹下[11]：

①执行makexp，检查要解算的RINEX格式或GAMIT认可的X开头的观测文件，正常运行后，按照提示依次输入有关工程的各类信息和参数；

②执行sh_sp3fit，生成g文件以及t文件；

③执行sh_check_sess，对生成的g文件进行检查，以查看session.info中有对应的卫星；

④执行makej，由广播星历文件生成钟差文件，即参考时刻卫星钟的钟偏以及钟漂；

⑤执行sh_check_sess，检查J文件，以查看session.info中有对应的卫星；

⑦执行fixdrv，生成接收机钟差多项式系数I文件以及批处理文件(b****y.bat)和相应的输入文件；

⑧执行csh b****y.bat，得到每天的计算结果文件。

2.3.2 平差处理流程

1)利用GLOBK的htoglb模块将H文件转换为二进制文件。

2)将所有*.glx文件做一个列表文件，命名为*.gdl。

3)执行globk单天平差计算，输入“glred 6 glred.prt glred.log *.gdl globk_comb.cmd”，得到单天平差结果文件。

2.4 解算结果分析

单时段解算的标准化均方根残差(normalized root mean square value，NRMS)是判断GAMIT基线解算结果质量好坏的一个重要指标。通常来说，NRMS值越小，基线解算精度越高；反之，精度越低。依据Q文件中的NRMS值对其结果进行衡量分析，比较理想的NRMS值应小于0.25；若大于0.5，说明处理过程中有可能存在未消除的大周跳或某一参数的解存在较大偏差；查看O文件中的基线解算结果和精度，从而进一步对基线解算结果进行分析[12-15]。

3 算例及精度分析

3.1 算例

选用2012-10-02(年积日第289天)福建省7个连续运行参考站(continuously operating reference stations，CORS)的原始观测数据进行解算，观测时间为24 h，历元间隔30 s。7个CORS站点分布如图1所示。

用7种星历对CORS站的数据进行了解算，并从解算完的基线中选择了14条，具体情况如表3所示。

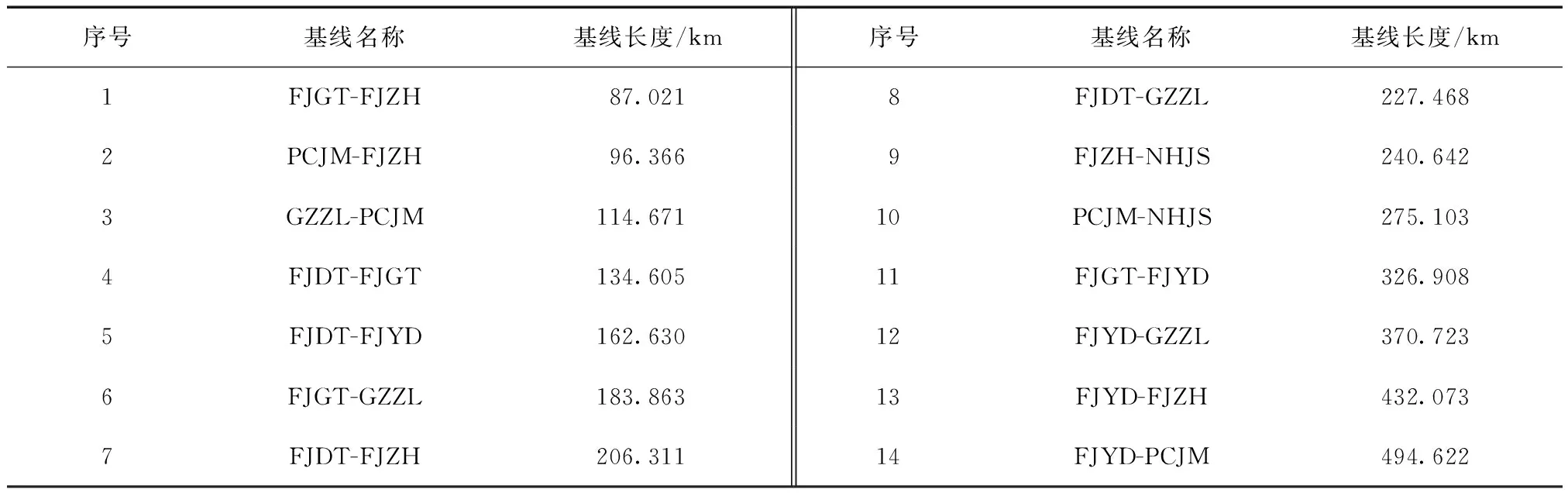
表3 GAMIT解算实验基线

3.2 精度分析

通常只要NRMS值符合要求，则可认为基线解算结果比较可靠。表4为不同的星历解算得到的NRMS值。从表中可以看到，几种星历解算的NRMS值都小于0.25，并且与最终精密星历解算的NRMS值之差仅为0.012，说明由快速星历和超快速星历得到的解算结果是合理的。

表4 7种星历解算验后NRMS值

为进一步比较解算结果的精度，对不同星历平差完成的基线坐标进行比较分析。解算结果以利用最终精密星历进行解算的结果为基准，将其他星历解算得到的基线坐标分量与之求差，得到基线解分别在北方向(N)、东方向(E)、天向(U)3个方向的差值，如图2、图3、图4所示。

从图2～图4中可以看出由快速星历解算得到的结果和最终精密星历解算得到的结果在3个方向上的差值都为零。这说明在本次基线解算实验中，快速精密星历和最终精密星历基线解算的测站坐标结果一致。超快速精密星历解算得到的结果与最终精密星历解算得的结果在3个方向上存在差异；当基线长度在370 km以内时，在N、E方向上差值基本在0.5 mm以内；当基线长度达到432和494 km时，差值在1～2 mm之间，且呈现随着基线增长差值逐渐增大的趋势。

4 结束语

本文使用不同星历对实测CORS站数据进行基线解算，通过这次基线解算实验以及工作中大量的基线解算经验，验证了在特定情况下，使用其他2种星历代替最终精密星历进行基线解算的可行性与准确性，且得出：当在无法获取最终精密星历但可以获取快速精密星历的的特殊情况下，可以使用快速精密星历代替最终精密星历进行高精度的基线解算与平差处理；当在无法获取上述2种星历但可获取超快速星历的特殊情况下，在处理小于400 km以内的中短基线数据时，可以使用超快速精密星历代替精密星历进行高精度的基线解算与平差处理。

[1] HERRING T A，KING R W，MCCLUSKY S C.GAMIT reference manual GPS analysis at MIT(Release 10 3)[EB/OL].(2015-06-16)[2017-01-19].http：//www.doc88.com/p-817688430780.html.

[2] 李征航，张小红.卫星导航定位技术及高精度数据处理方法[M].武汉：武汉大学出版社，2010.

[3] 党亚民，秘金钟，成英燕.全球导航卫星系统原理与应用[M].北京：测绘出版社，2007.

[4] 刘大杰，施一民，过静珺.全球定位系统(GPS)的原理与数据处理[M].武汉：武汉大学出版社，2005.

[5] 张勤，李加权.GPS测量原理及应用[M].北京：科学出版社，2005.

[6] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2010.

[7] 高旺，高成发，潘树国，等.基于广播星历的GAMIT基线解算方法及精度分析[J].测绘科学，2014，39(8)：54-57.

[8] 曹炳强，成英燕，许长辉.海潮模型对连续跟踪参考站数据解算的影响：以福建省为例[J].测绘科学，2015，40(12)：108-111.

[9] 黄功文，王斌，王延伟.高精度GPS控制网基线重复性检验与质量分析[J].测绘通报，2011(7)：9-11.

[10] 王霞迎.BDS-GPS基线解算算法研究[D].北京：中国测绘科学研究院，2014.

[11] 王武星，顾国华.利用基准站观测资料确定GPS卫星轨道[J].大地测量与地球动力学，2003，23(3)：112-115.

[12] 张双成，曹海洋，高涵，等.基于GAMIT的GPS短基线解类型分析及应用[J].测绘通报，2011(10)：27-29.

[13] 赵建三，杨创，闻德保.利用GAMIT进行高精度GPS基线解算的方法及精度分析[J].测绘通报，2011(8)：5-8.

[14] 曹炳强，成英燕，许长辉，等.间距分区法在解算卫星连续运行站数据中的应用[J].测绘通报，2016(11)：15-17.

[15] 万军，成英燕，党亚民，等.陆态网测站高精度解算分区方案[J].测绘科学，2016，40(4)：1-4.