BDS在轨卫星原子钟性能评估分析

王省超 ，贾小林，艾青松，任志远，沈洪霞

(1.长安大学 地质工程与测绘学院，西安 710054;2.地理信息工程国家重点实验室，西安 710054; 3.西安测绘研究所， 西安 710054;4.中国科学院测量与地球物理研究所 大地测量与地球动力学国家重点实验室，武汉 430077;5.中国科学院大学，北京 100049;6.内蒙古鄂尔多斯市造林总场，内蒙古 鄂尔多斯 014300)

0 引言

我国的北斗(区域)卫星导航系统(BeiDou navigation system，BDS)已于2012-12-27正式开始运行[1]。目前BDS卫星搭载的是铷钟，其精度和稳定性相较于全球定位系统(global positioning system，GPS)和伽利略卫星导航系统(Galileo navigation satellite system，Galileo)星载原子钟存在一定的差距[2]。国内外的学者对全球卫星导航系统(global navigation satellite system，GNSS)星载原子钟的性能进行了大量的研究：文献[3]基于3年的卫星钟差数据对BDS卫星钟性能进行了评估和分析；文献[4]对原子钟时频分析的理论与方法进行了系统的介绍；文献[5]对星载原子钟完好性监测方法进行了较深入的研究。利用较长时段的卫星钟差数据进行星载原子钟性能评估分析，对系统的性能评估和卫星钟差确定及预报等具有重要的作用[6-7]。随着BDS的不断运行，目前BDS第一批发射的卫星已经接近寿命末期，对BDS星载原子钟性能进行较为全面的评估分析尤为重要。

本文对BDS星载原子钟的频率准确度、漂移率、稳定度和钟差噪声进行评估分析，以期为相关研究提供参考。

1 噪声分析建模

频率准确度、漂移率和稳定度是星载原子钟性能分析的主要指标[8-10]。

频域的稳定性分析用于描述噪声能量随频率的变化，并且可以反映原子频标受噪声影响的本质。噪声的幂率谱模型公式[11-13]为

(1)

式中：Sy(f)为频率数据的单边功率谱密度，单位为Hz-1；f为傅氏频率，单位为Hz；hα为噪声强度的系数；噪声类型的整数用α表示。卫星钟噪声类型分类列于表1。

表1 噪声类型、α值、μ值对照

常规的幂律谱噪声识别方法有斜率法、B1偏差因子法和LAG1自相关法等。实际应用中需要分析平滑因子较长的各个时间内的噪声类型，因此主要采用LAG1自相关法对GNSS星载原子钟进行噪声分析。本文采用LAG1自相关法对BDS星载原子钟进行噪声分析。

自相关函数的定义[14]为

(2)

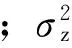
其估计形式为

以护士对器官捐献态度得分为因变量，护士婚姻状况、子女情况、文化程度、职称、月收入为自变量，进行多元逐步回归分析，界定α入=0.05，α出=0.10。结果显示，职称、有无子女、文化程度3个因素进入回归方程（见表4）。

(3)

式中k=1时，即可得LAG1自相关系数r1。

基于LAG1自相关函数法识别噪声，当σ<0.5时，离散的噪声序列是平稳的，且LAG1自相关函数识别噪声可以表示为ρ1=σ/(1+σ)，得到噪声类型σ=r1/(1+r1)。当噪声序列不满足平稳条件时，应对其进行差分处理，直至得到的噪声序列转化为平稳状态(σ<0.25)为止。在平稳条件下判定噪声类型的准则是

p=-round(2σ)-2d。

(4)

式中：round为就近取整函数；d为差分计算的阶数。如果参与计算的时间序列是频率数据时α=p；若是相位数据，则α=p+2。算法的具体步骤如图1所示。需要说明的是，利用LAG1自相法进行噪声识别时，首先要去除钟差数据粗差和不连续点。实验表明采样点在30以上时，对噪声类型的判断才较为准确。

2 原子钟性能评估分析

本文采用德国地学中心提供的事后精密钟差产品对BDS星载原子钟性能进行评估分析。数据的采样间隔为300 s，选用2016-01—2017-03时长456 d的数据进行频率准确度、漂移率、稳定度和钟差噪声分析等。其中C15卫星钟差数据较少，卫星编号存在变更，全文不对其做统计分析。

2.1 钟差数据质量分析

图2为各颗BDS卫星的钟差序列图。可以发现，BDS星载原子钟在长期运行过程中存在一定的调相、调频和数据缺失现象。在3类卫星中，地球静止轨道(geostationary Earth orbit，GEO)卫星的相位跳变最为显著，中圆地球轨道(medium Earth orbit，MEO)卫星较为平稳；因此在进行该时段内的钟差预报和卫星钟性能评估时，首先要对钟差序列进行分段处理，保证数据的质量。

图3为本文选用数据整天缺失的统计情况。可以看出：BDS GEO卫星钟差数据整天缺失比较严重，除C05卫星外，钟差数据缺失率都在10 %以上；倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)次之；MEO卫星钟差数据完整性较好，其中C11和C14卫星整天缺失率为零(C13卫星2016-10才有数据，数据缺失比较严重，数据缺失率不作统计)。

2.2 准确度评估分析

2.3 漂移率评估分析

与计算频率准确度一样，按照单月作为处理单元，对BDS星载原子钟频率漂移率进行评估分析，如图5所示。可以看出，BDS星载原子钟的日漂移率基本处于1.0×10-14s量级。其中C14卫星频率漂移现象最为明显，整个时段都处于1.0×10-13s量级，并且在2016-07出现异常，日漂移率处于1.0×10-12s量级；C06卫星2017-02和2017-03日漂移率较差，日漂移率处于1.0×10-13s量级；C08卫星2016年前7个月日漂移率也较差；C13卫星除2017-01和2017-03外，其他几个月日漂移率也处于1.0×10-13s量级。

2.4 稳定度评估分析

本文采用哈达玛方差对BDS星载原子钟进行稳定度评估分析。图6所示为天稳定度统计结果。可以看出，BDS在轨卫星钟的天稳定度基本处于1.0×10-14s量级。其中C06卫星和C13卫星钟的天稳定度较差；C14卫星在2016-07出现较大的异常。从日漂移率分析发现，C14卫星在2016-07同样出现了较大的异常现象，对此，本文对2016-07 C14卫星分析其频率数据，发现该月份C14卫星发生了较大的调频现象。

2.5 钟差模型噪声分析

以d为单位，对钟差数据进行2次多项式拟合，得到其拟合残差，并计算全时段残差的精度(STD)(如图7所示)。

从图7可以看出，BDS星载原子钟噪声的随机分布和噪声水平(STD)除个别卫星外分别在2和0.8 ns以内，全时段内不论噪声的随机分布还是噪声水平MEO卫星均优于GEO卫星和IGSO卫星。所有卫星中，C14卫星噪声分布最为均匀和平稳，C06和C13卫星的钟差序列拟合精度明显低于其他卫星，尤其是C06卫星，大部分时段的拟合残差都比较大，进入2017-02以后拟合残差突然变小，且相对比较稳定。C13卫星自2016-10-15开始有数据，随着时间的增加，卫星钟差拟合残差逐渐变大，进入2017-01以后拟合残差突然变小，且也是相对比较稳定。这与C06卫星和C13卫星分别在2017-02-14和2017-01-20切换了相对稳定的原子钟有关。

本文对全时段的频率准确度、漂移率和稳定度取其均值(准确度和漂移率取其绝对值均值)作为性能分析的结果，对BDS星载原子钟性能进行比较分析(如表2所示)。需要说明的是为了更为准确地评估BDS所有卫星性能指标，各项指标取绝对值均值时，对于当月出现较大或多次调频的分析结果视为粗差剔除。C06和C13卫星钟性能极不稳定，且C13卫星全时段只有5个多月的数据，稳定度指标取绝对值均值时不做粗差处理，2颗卫星不参与对IGSO卫星性能指标取绝对值均值计算。

表2 卫星钟性能综合分析结果 s

从表2中可以看出：BDS卫星导航系统中，C06和C13卫星星载原子钟整体性能较差；MEO卫星星载原子钟的稳定性(万秒稳和天稳)略优于IGSO卫星；GEO卫星最差。

2.6 噪声识别

本文采用LAG1自相关法对BDS在轨卫星钟进行较长平滑因子的各个时间内的噪声类型分析，选用数据相对完整的2016-05-11—2016-05-31(共21 d的数据进行试验)。图8所示为BDS GEO、IGSO和MEO卫星钟噪声分析的结果(C13卫星数据缺失)。从图中可以看出，进行钟差噪声识别分析时随着平滑时间的变化，噪声类型也发生变化[15](参见表1)。总的来说，影响BDS 3类轨道星载原子钟的噪声主要为WFM、FFM和RWFM。其中所有卫星中C09卫星和C10卫星随着平滑时间的变化，噪声分析的结果呈现出极大的跳跃性，不能准确辨识其噪声类型。出现该现象应与该卫星原子钟的频率序列存在周期性波动和明显的频率漂移现象有关：分析其C09卫星钟的频率序列变化(图9所示)，C09卫星钟的频率序列存在明显的频率漂移现象；分析C10卫星钟的频率序列变化(图10所示)，C10卫星钟的频率序列存在明显的周期性波动现象。

3 结束语

本文基于较长时间段的钟差产品，对BDS星载原子钟性能进行评估和分析。得出以下结论：

1)BDS星载原子钟在长期运行过程中存在一定的调频、调相和数据缺失现象，整体上GEO卫星的相位跳变较为明显，IGSO次之，MEO卫星数据完整性较好；

2)BDS星载原子钟频率准确度处于1.0×10-11s量级，日漂移率处于1.0×10-14s量级，万秒稳和天稳处于1.0×10-14s量级；

3)所有卫星中，C06卫星和C13卫星星载原子钟整体性能较差，3类轨道卫星中，MEO卫星星载原子钟稳定性略优于IGSO卫星，GEO卫星星载原子钟稳定性最差；

4)全时段内不论是噪声的随机分布还是噪声水平MEO卫星均优于GEO卫星和IGSO卫星；

5)整体上来看，影响BDS在轨卫星原子钟的噪声主要为WFM、FFM和RWFM。

鉴于BDS分别于2017-01和2017-02进行了C13卫星和C06卫星钟切换，后续的工作中将对其卫星钟切换前后的性能进行长期的比较评估分析，为相关研究提供参考。

致谢：感谢iGMAS中心提供的数据支持。

[1] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报，2010，39(1)：1-6.

[2] 孙大伟.GNSS星载原子钟性能分析理论与算法研究[D].西安：长安大学，2016.

[3] 王宇谱，吕志平，王宁.BDS星载原子钟长期性能分析[J].测绘学报，2017,46(2)：157-169.

[4] 郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州：信息工程大学，2006.

[5] 唐升，刘娅，李孝辉.星载原子钟自主完好性监测方法研究[J].宇航学报，2013，34(1)：39-45.

[6] 李作虎.卫星导航系统性能监测及评估方法研究[D].郑州：信息工程大学，2012.

[7] 唐桂芬，许雪晴，曹纪东，等.基于通用钟差模型的北斗卫星钟预报精度分析[J].中国科学：物理学 力学 天文学，2015,45(7)：79502.

[8] 贾小林，冯来平，毛悦，等.GPS星载原子钟性能评估[J].时间频率学报，2010，33(2)：115-120.

[9] 张清华.GNSS监测评估理论与方法研究[D].郑州：信息工程大学，2014：102-139.

[10] GRIGGS E，KURSINSKI E R，AKOS D.An investigation of GNSS atomic clock behavior at short time intervals[J].GPS Solutions，2014，18(3)：443-452.

[11] 田婕.GPS/BDS原子钟性能分析及钟差预报模型研究[D].西安：长安大学，2015.

[12] BARNES J A，CHI A R，CUTLER L S，et al.Characterization of frequency stability[J].IEEE Transactions on Instrumentation & Measurement，1971，IM-20(2)：105-120.

[13] 罗璠，李建文，黄海，等.北斗卫星钟稳定性分析及噪声识别[J].测绘科学技术学报，2014，25(1)：34-37.

[14] 杨文可.时频信号相位噪声分析与辨识研究[D].长沙：国防科学技术大学，2008.

[15] 于合理，郝金明，宋超，等.卫星钟系统偏差对精密单点定位精度的影响[J].测绘科学技术学报，2013，30(2)：136-139.