复杂环境下抗NLOS干扰的定位算法

高端阳，李 安，傅 军

(1.海军工程大学 导航工程系，武汉 430033；2.海军工程大学 训练部，武汉 430033)

0 引言

随着基于位置的服务(location-based service，LBS)快速发展，所取得的各项科研及应用成果给人们的日常生活带来了极大的便利；如何提供更高性能、更全面的位置服务成为当前科研工作人员关注的重点。室外环境下，由于全球卫星导航定位系统技术的日渐成熟，室外定位技术已得到很好解决。而室内环境下，无线信号容易受到建筑物遮挡、多路径效应、非视距(non line of sight，NLOS)传播等因素的影响，单纯的无线定位方式存在精度不高，且容易产生信号突变的现象，如何提高室内定位精度成为当前的研究热点。文献[1]回顾了近10年来的相对室内定位的发展，并指出了今后的研究方向。文献[2]采用神经网络和遗传算法相结合的射频识别(radio frequency identification，RFID)室内定位方法，但是实现较高的定位精度需要较多的阅读器。文献[3]利用低精度的微机电系统(micro-electro-mechanical system，MEMS)器件实现了3维室内定位，由于误差随时间积累，无法满足长时间的定位要求。文献[4]利用信标节点的距离差分信息，修正目标节点的距离信息，减少了计算量，较少的信标节点也能保证定位精度。在非视距条件下，文献[5]提出基于到达时间(time of arrive，TOA)测量与惯导信息融合的定位算法，有效减少了非视距传播对定位结果的影响。文献[6]采用卡尔曼滤波处理TOA测量值，提高了定位精度。文献[7]用卡尔曼滤波对估算位置坐标进行滤波处理，提高了无线定位方式的性能和稳定性，但依然存在用户位置不连续的问题。文献[8]采用超宽带(ultra-wide band，UWB)和捷联惯导系统(strapdown inertial navigation system，SINS)组合方式，设计卡尔曼滤波器，抑制误差的同时提高了室内定位的精度。文献[9]采用了一种基于无迹卡尔曼滤波的无线定位与惯性导航单元(inertial measurement unit，IMU)组合的室内定位算法，降低了无线定位结果的波动幅度，又解决了IMU累积误差问题。文献[10]提出了联合全球定位系统(global positioning system，GPS)和无线局域网络的组合定位方法，采用联邦卡尔曼联滤波算法实现室内外的无缝定位与导航，但定位性能受环境影响较大。

针对大型船舶舱室内无线定位技术的无线信号传播过程中存在非视距传播、多路径效应的问题，以及少数基站(base station，BS)在未知情况下会出现测距误差较大的问题等情况，本文提出一种基于测距的自适应定位算法，在基站冗余情况下将基站任意组合，并引入面积因子评价机制，选择最优的基站组合方式用于定位解算，以提高定位精度。

1 室内定位技术

1.1 定位手段

目前用于室内定位的手段[11]主要有无线局域网(wireless fidelity，WiFi)定位、发光二极管(light-emitting diode，LED)灯光定位、蓝牙定位、射频标签定位、超宽带(ultra-wide band，UWB)无线定位、ZigBee定位、地磁定位、超声波定位、计算机视觉定位等，每种定位方式都有其适用范围和优缺点。其中无线定位系统主要有UWB定位、Chirp扩频(chirp spread spectrum，CSS)定位、ZigBee定位、WiFi定位，有源或无源无线射频识别(radio frequency identification devices，RFID)定位、基站定位等。比较市场上主流开发商的各种无线定位系统的定位精度和成本，性能总结如表1所示。

表1 无线定位系统性能对比

通过对比分析，不难看出第2类无线定位系统有着其独特的优势，定位精度合适且定位成本易于接受，适用范围较广，性价比较高。当然每种室内定位技术在增加硬件数量的情况下，定位精度都会有所提高，但是成本也会随之增加。

1.2 定位原理

目前用于定位的方法[11]主要有基于距离的定位方法、基于到达时间差的定位方法、基于到达角度的定位方法、基于信号指纹的定位方法等，本文主要介绍基于距离的定位原理。测距定位就是通过测量目标点到基站之间的距离，利用多个距离位置线来确定目标点的位置坐标。平面定位中该方法至少需要3个测距信息，通过测量目标点到各基站之间的无线信号传播时间来获取测距信息。以2维位置解算为例，图1中虚线为理想情况下平面定位原理图。

在实际工程应用中，由于存在非视距传播和多路径效应等因素影响，目标点到各基站之间的测量距离通常都会大于实际距离，此时定位效果如图1中实线所示。

1.2.1 解算方程的建立

理想情况下，目标点位于以各个基站为圆心、测距长为半径的圆上。设基站坐标分别为BS1(x1,y1),BS2(x2,y2),…,BSn(xn,yn)，目标点位置为(x,y)，目标点到第i个基站之间的测量距离为di，故目标点与基站之间存在以下几何关系，表达式为

(1)

1.2.2 泰勒级数解算

由于多路径、非视距传播等因素的影响，实际测量中会存在一定的误差，目标点与基站之间的测量距离通常都会大于真实距离；因此直接通过式(1)求解无法得到满足所有方程的唯一解。为了提高解算的位置精度，可以通过增加基站数目的办法，使得式(1)中方程个数大于未知数的个数，变为超定方程的求解问题。超定方程的求解可以利用泰勒级数法求解，式(1)中的方程为非线性方程，通过泰勒级数展开并简化对其线性化。

1)给定目标点初始位置为(x0,y0)，与真值之间的误差设为δx、δy，则

(2)

2)将式(1)在(x0,y0)处用泰勒级数展开，为了便于计算，将2次及以上项忽略，则

(3)

整理得

(4)

然后采用最小二乘法解算目标点的位置坐标，令

方程矢量矩阵表示为

Aδ=b。

(5)

最小二乘求解为

δ=(ATA)-1ATb。

(6)

因此目标点的位置为

(7)

2 基于测距的自适应模型

2.1 存在的问题

大型舱室内，基于测距的定位方法在实际应用中通常会存在目标点到某个基站之间的测距信息误差较大，而到其他基站测距信息较为准确的现象，如图2所示。出现该现象一方面因为舱室内环境相比较于室外环境复杂多变，房间的墙壁、物品的摆放以及人员的走动都可能会导致无线信号的传播存在非视距、多路径等因素的影响，当目标点与该基站之间有物品的遮挡，无法实现目标点与基站之间无线信号的视距传播时，测距信息就会存在较大的非视距传播误差；另一方面由于未知情况下基站存在故障，也可能会导致目标点到该基站之间的测距信息出现误差较大的现象。

若将误差较大的测距信息用于位置解算，该解算的结果也将存在较大误差，降低定位精度。

2.2 自适应模型

在目标点位置解算过程中，发现某个基站的测距信息误差较大，若该基站数据依然用于目标位置解算，定会影响定位精度。在基站冗余的情况下，若能把该基站数据剔除，使用误差较小的基站测距数据解算位置，将会提高定位精度。本文提出的自适应算法着重于解决少数基站测距数据误差较大问题，算法框图如图3所示。

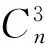
(8)

式中i、j、k为n个基站中的任意3个。然后判断交点是否都处于3个基站圆位置线上或者内部。若满足

(9)

则说明交点Cm处于3个基站圆位置线上或者内部，其中Cm为6个交点中的任意一个。当任意3个基站之间满足

(10)

此时位于3个基站圆位置线上或内部的交点仅有3个，说明该3个基站测距较为理想，可用于目标点位置解算。设3个交点分别为A(xA,yA)、B(xB,yB)、C(xC,yC)，为了减少计算量，此时所得第i、j、k3个基站组合的圆位置线相交的公共区域面积Sijk近似为3个交点组成的三角形面积。则有

(11)

定义面积因子

(12)

比较不同基站组合之间的公共区域面积大小，选取面积最小时对应的3个基站用于目标点位置解算。J的值越小，通常情况下定位精度越高。

3 实验及结果分析

3.1 实验环境

为了验证算法的性能，本文采用Nanotron公司研发的基于CSS定位原理的Nano定位系统进行实验，系统由4个基站和1个定位标签组成。实验在大会议室进行，将基站布局在房间的4个角落，在中间区域选择9个参考点，实验平面场景如图4所示。

1)房间为11 m×10 m长方形区域，定位系统布局如图4所示；

2)基站高度为2 m，定位标签高度为1 m，采集标签到各个基站之间的距离数据；

3)基站放于房间4个角落，坐标依次为A(0，0)、B(9，0)、C(9，9.6)、D(0，9.6)；

4)标签分别放置于9个参考点，坐标依次为(4.2，4.2)、(3，2.4)、(4.2，2.4)、(6，2.4)、(6，4.2)、(6，6)、(4.2，6)、(3，6)、(3，4.2)。

3.2 方案设计及数据采集

将各个基站按照上述实验场景布置，分别对4个基站依次进行实验。通过在基站与目标之间摆放书柜，造成该基站受到非视距传播的干扰，并将目标点依次放于9个参考点位置，采集目标点到各个基站之间的距离信息，采集的部分数据如图5所示。

图5数据共分为4列，分别表示4个基站A、B、C、D依次受到干扰情况下所采集的数据信息。每一列中4行为一组，每行表示目标与该基站之间的测距信息，且每行中的第一个数表示基站与目标之间的距离，第2个数表示目标代号，第3个表示基站代号，001、002、003、004对应A、B、C、D，第4个数表示测距信息是否正常，015表示测距正常，其他值表示测距异常。由图5可以看出：当基站与目标之间受到非视距传播时，测距信息出现异常，测量距离远大于真实距离；而且第四列出现一组数据第四个基站测距无效现象，即第四个基站时而正常，时而故障。

3.3 数据处理及分析

按照采集的目标点到各个基站之间的距离信息，分别利用传统的坐标位置解算方法(即将所有基站数据参与目标点的位置解算)和本文改进的自适应算法进行解算，同时采集定位系统自身输出的定位结果进行统计分析，比较3者之间在各个参考点的平均定位误差。分别见表2和图6。

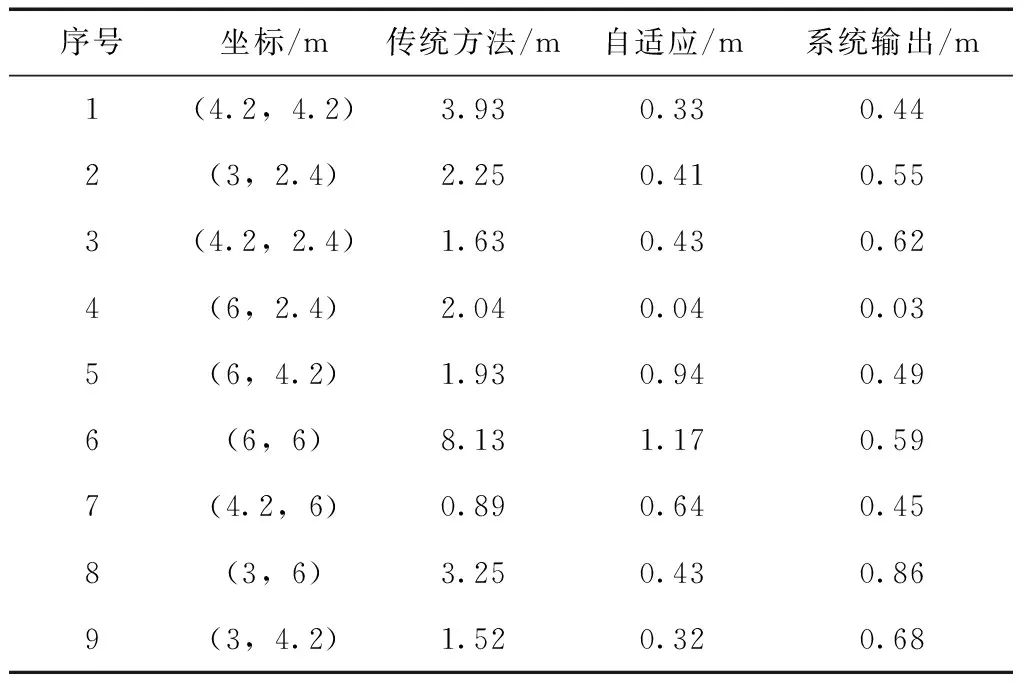
表2 3种不同方式在各参考点的平均误差

图6表示3种不同方式在各个参考点的平均误差，其中横坐标数值参考点的序号和坐标值参照表2。综合表2和图6可知，传统坐标位置解算由于没有排除误差较大基站的影响，将所有可用的基站均参与目标点的坐标位置解算，平均误差在2 m左右，在某些特殊情况下误差更大。自适应算法解算出的坐标位置与系统直接输出的坐标位置在各个参考点的平均误差基本小于1 m，说明改进的自适应算法在定位精度上有较大的提高。

4 结束语

本文在分析传统定位算法的不足的基础上，提出一种自适应定位算法，通过分析多个圆位置线之间的关系，引入面积因子比较机制，剔除测距误差较大的基站数据，选择最优的基站组合参与定位解算，提高了定位精度。该算法使得定位系统具有较好的环境适应能力，即使在少数基站存在较为严重的非视距传播或者少数基站发生故障时也具备良好的定位性能。而对于无线传播的多路径效应问题，还有待进一步研究和解决。

[1] STYLIANOU G.Relative indoor spatial tracking and navigation[J].International Journal of Wireless & Mobile Computing，2015，9(1)：8-26.

[2] CHEN R C，HUANG S W，LIN Y C，et al.An indoor location system based on neural network and genetic algorithm[J].International Journal of Sensor Networks，2015，19(3/4)：204-216.

[3] ZHENG L，ZHOU W，TANG W，et al.A 3D indoor positioning system based on low-cost MEMS sensors[J].Simulation Modelling Practice & Theory，2016，65：45-56.

[4] 李体红，丰树谦.室内无线传感网络差分定位算法研究[J].计算机仿真，2010，27(7)：102-104.

[5] 傅军，朱涛，李峰.一种NLOS环境下TOA与惯导信息的融合定位方法[J].海军工程大学学报，2015，27(5)：34-38.

[6] 李峰，朱涛，傅军.一种基于卡尔曼滤波的TOA定位算法[J].自动化与仪器仪表，2013(1)：116-118.

[7] 赵永翔，周怀北，陈淼，等.卡尔曼滤波在室内定位系统实时跟踪中的应用[J].武汉大学学报(理学版)，2009，55(6)：696-700.

[8] 刘见辉，王冬，刘凤英，等.高精度UWB/SINS组合室内定位系统研究[J].导航定位学报，2016，4(2)：53-56，86.

[9] 曾辉，邓中亮，薛宸，等.基于无迹卡尔曼滤波的无线定位与IMU组合室内定位算法[EB/OL].[2017-02-18].http：//d.wanfangdata.com.cn/Conference/8474978.

[10] 马燕，袁蔚林，陈秀万，等.基于WiFi与GPS组合定位算法的无缝定位方法研究[J].地理与地理信息科学，2013，29(3)：6-9，16.

[11] 赵锐，钟榜，朱祖礼，等.室内定位技术及应用综述[J].电子科技，2014，27(3)：154-157.