非接触变压器磁路模型及结构优化

徐罗那， 杜玉梅， 史黎明

(1. 中国科学院电力电子与电气驱动重点实验室， 中国科学院电工研究所, 北京 100190;2. 中国科学院大学电子电气与通信工程学院, 北京 100049)

1 引言

感应电能传输(Inductive Power Transfer，IPT)是基于磁场耦合实现电能传输的供电技术，利用原、副边完全分离的非接触变压器，通过高频磁场耦合来传输电能。相比于传统的利用接触导体进行供电的方式，非接触供电具有使用方便、安全可靠、受环境影响小、维护成本低等优势[1,2]，日益成为研究热点，并在工业生产、医疗、交通和日常生活等领域获得一定应用[3-5]。

非接触供电系统由直流电源、逆变器、非接触变压器、整流电路和负载组成，其示意图如图1所示。逆变器将直流电逆变成高频交流电，作为非接触变压器原边绕组的输入，IPT系统通过非接触变压器相互分离的原、副边绕组之间的感应耦合将电能传递到副边，整流后供给负载。因此，提高非接触变压器的耦合性能是提高系统能量传递效率的关键[6-8]。

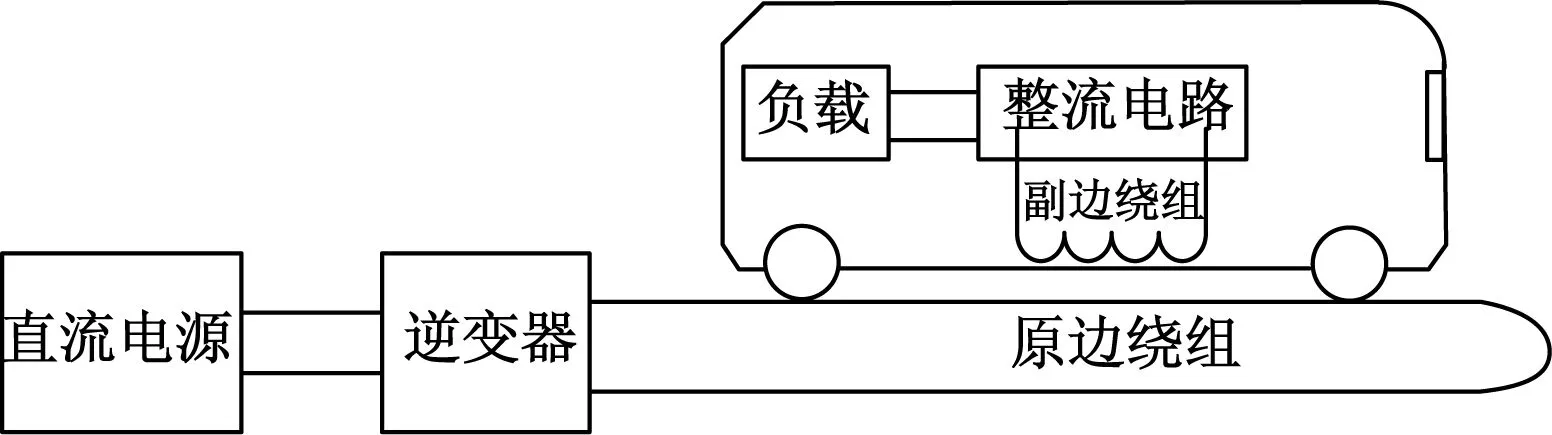
图1 IPT系统示意图Fig.1 IPT system

为了提高非接触变压器的耦合系数和能量传输效率，现有文献对非接触变压器的分析主要从电路和磁路两个方面展开。

从电路角度，通常采用不同的补偿拓扑，使非接触变压器工作在谐振状态，从而提高输出侧的感应电压[9-12]。文献[9]对比了不同补偿拓扑下的电压电流增益、功率因数计算。文献[13-15]给出了多种补偿拓扑中补偿电容的选取依据。从磁路角度，分析非接触变压器周围的磁场，提取磁路模型，对非接触变压器的结构进行优化，从而提高非接触变压器的能量传输效率[16-19]。文献[16]从磁路角度分析了气隙为5mm的原、副边结构对称的U型磁心非接触变压器，给出系统传输功率与非接触变压器结构参数的关系，并对匝数进行优化计算，但没有考虑漏磁通的影响，因而计算结果存在一定误差。文献[17]通过将非接触变压器的磁通路径划分成便于计算的形状规则的磁通管来计算磁阻，从而给出非接触变压器的耦合系数关于几何参数的表达式，并提出优化方法，增大原、副边绕组之间的互感，在10mm气隙下，非接触变压器的耦合系数达到0.6，系统效率最高达到90%以上。对于原、副边结构不同，且气隙较大的非接触变压器，磁通管划分存在困难，现有的研究方法并不适用。在对非接触变压器的结构优化方面，现有文献通常通过增大互感来实现耦合系数的提高，缺少对非接触变压器的原、副边自感的研究[20]。

本文针对原、副边结构不对称，且气隙较大的非接触变压器，根据线性系统的叠加原理，利用有限元(Finite Element Method，FEM)计算软件，分别分析非接触变压器在副边开路和原边开路时其周围的磁场分布，提取出磁路模型，并推导得到原、副边电感及耦合系数的近似计算公式。根据磁路模型，以提高耦合系数为目标，优化非接触变压器的结构，提出一种梯形绕组截面的绕组布置方式。以系统效率最大为目标，对原、副边绕组匝数关系进行优化计算。最后，对基于磁路模型设计的非接触变压器的电感及耦合系数理论计算与仿真结果进行对比验证。

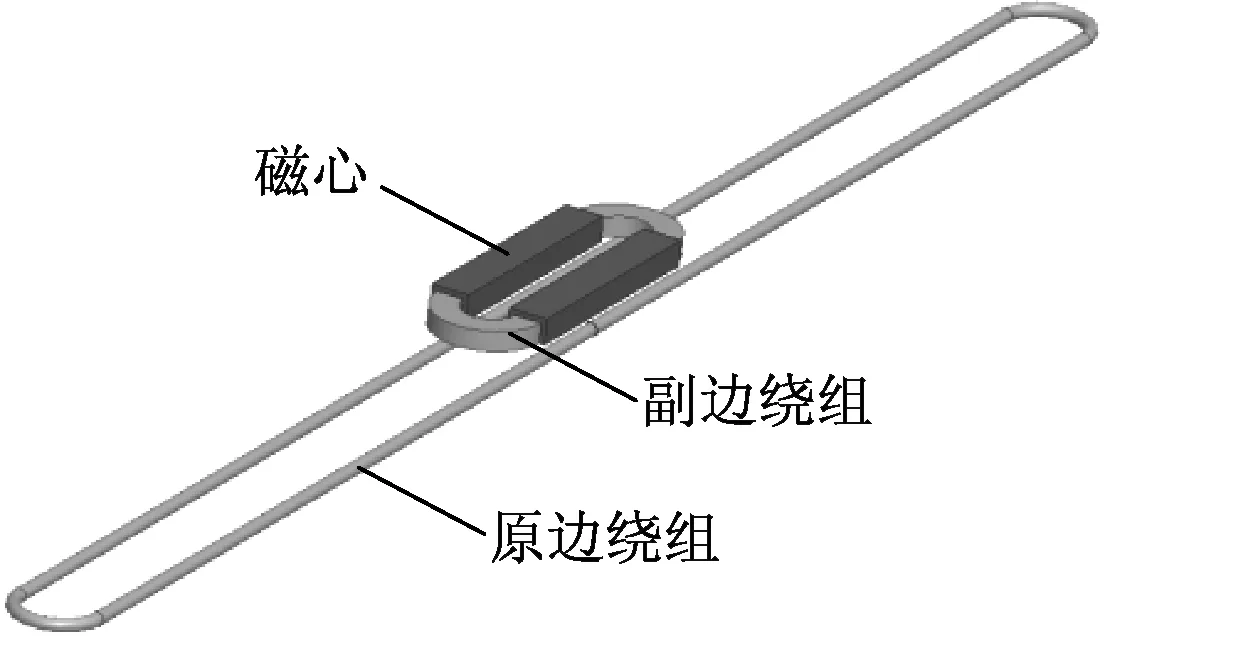
图2 非接触变压器示意图Fig.2 Contactless transformer schematic

2 磁路模型

图2为一种应用于轨道交通领域的非接触变压器，由沿轨道敷设在地面上的原边绕组和固定在车底的副边绕组组成。该非接触变压器采用原边绕组1匝线圈，副边绕组多匝线圈，仅副边布置磁心的结构。由于非接触变压器的原、副边绕组回路两侧结构对称，因此本文仅对非接触变压器的一侧进行磁路分析，非接触变压器另一侧的磁场分布、磁通分区、磁阻计算与之分别相同。

由于副边绕组匝数较多，当非接触变压器工作在额定工况下，副边电流产生的磁场与原边电流产生的磁场不同，使得整体分析非接触变压器的磁路十分复杂。由于此时磁心未达到饱和，可以将系统拆分成两个磁路，即原边开路和副边开路两种情况，然后将其线性叠加。

2.1 副边开路

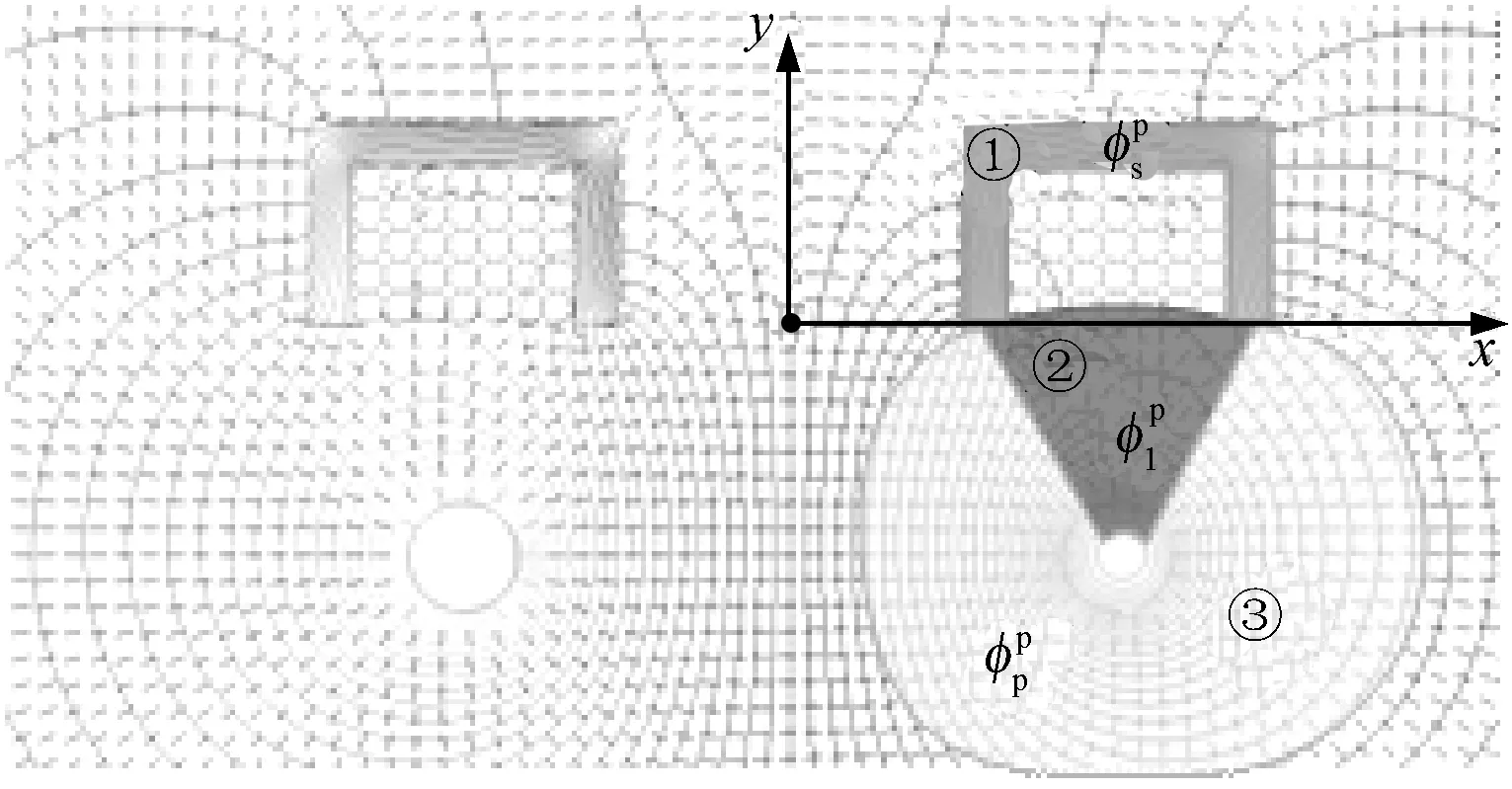
图3 副边开路时的磁场分布Fig.3 Magnetic field distribution at secondary open-circuit

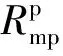
图4 副边开路时的等效磁路Fig.4 Reluctance circuit at secondary open-circuit

根据磁路欧姆定律，可以写出副边开路时的磁路方程：

(1)

2.2 原边开路

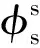
图5 原边开路时的磁场分布Fig.5 Magnetic field distribution at primary open-circuit

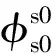
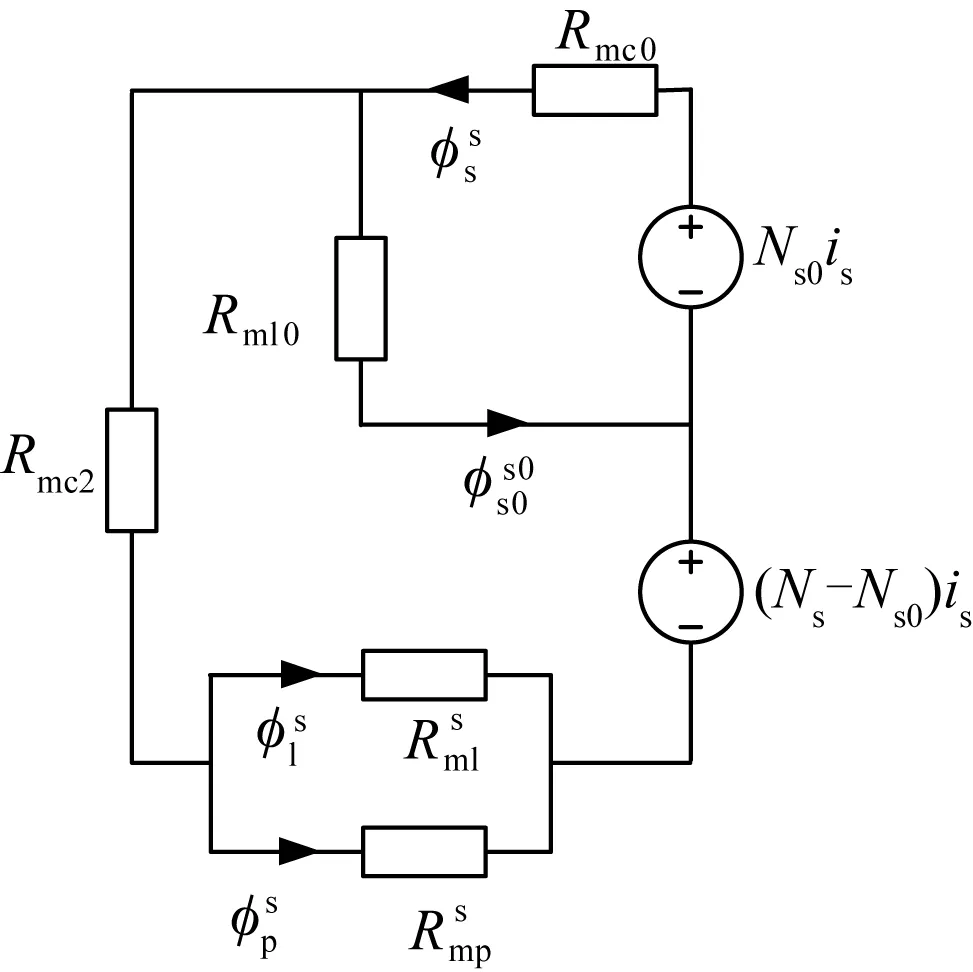
图6 原边开路时的等效磁路Fig.6 Reluctance circuit at primary open-circuit

根据磁路欧姆定律，可以得到原边开路时的磁路方程：

(2)

结合副边开路和原边开路两种情况，可得到所研究非接触变压器的磁路模型，即由式(1)和式(2)叠加。

3 磁阻及耦合系数计算

3.1 电感及耦合系数表达式

根据磁路模型，可以得到非接触变压器原、副边线圈所匝链的磁链分别为：

(3)

(4)

根据自感、互感的定义，即

原边自感Lp=dψp/dip

(5)

副边自感Ls=dψs/dis

(6)

原边对副边的互感Mps=dψp/dis

(7)

副边对原边的互感Msp=dψs/dip

(8)

结合非接触变压器的等效磁路，可以得到原、副边自感和互感的计算式如下：

(9)

(10)

(11)

(12)

式(10)和式(11)中，为简化表达式，引入变量Rma：

(13)

并且，在线性磁媒质中有：

M=Mps=Msp

(14)

根据非接触变压器耦合系数的定义：

(15)

将式(9)～式(14)代入式(15)，就可以得到用磁阻表示的耦合系数表达式。

由于本文所研究的非接触变压器的气隙较大，磁场分布复杂，难以通过将整个磁场分割为几何形状规则的磁通管并采用解析计算的方法来求解磁阻，因此采用有限元计算的方法进行辅助计算。

由非接触变压器所在空间的B和H分布，根据磁阻的定义，即

(16)

可以得到磁路模型中非接触变压器各个区域的磁阻值。积分路径根据图3和图5对磁通的划分来进行选择。

3.2 磁阻优化方法

通过电感的磁阻表达式，可以从理论上找到优化耦合系数的方式。化简式(12)得到：

(17)

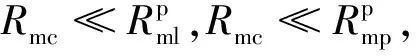
(18)

因此，要提高互感，应当减小原边绕组周围区域的磁阻，可以通过在原边布置磁心来实现。

对互感的另一个表达式(11)进行化简，得到：

(19)

同样地，有Rmc0≪Rml0，所以式(19)可以近似为：

(20)

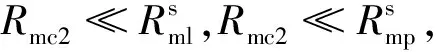
(21)

因此Mps可以进一步近似简化为：

(22)

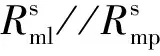
4 非接触变压器结构优化

根据磁路模型及耦合系数的分析结果，对非接触变压器的结构进行优化，以提高耦合系数。

4.1 原边结构

基于第3节的分析，在原边绕组周围布置磁心来提高耦合性能。建立原边带磁心的非接触变压器模型，如图7所示。

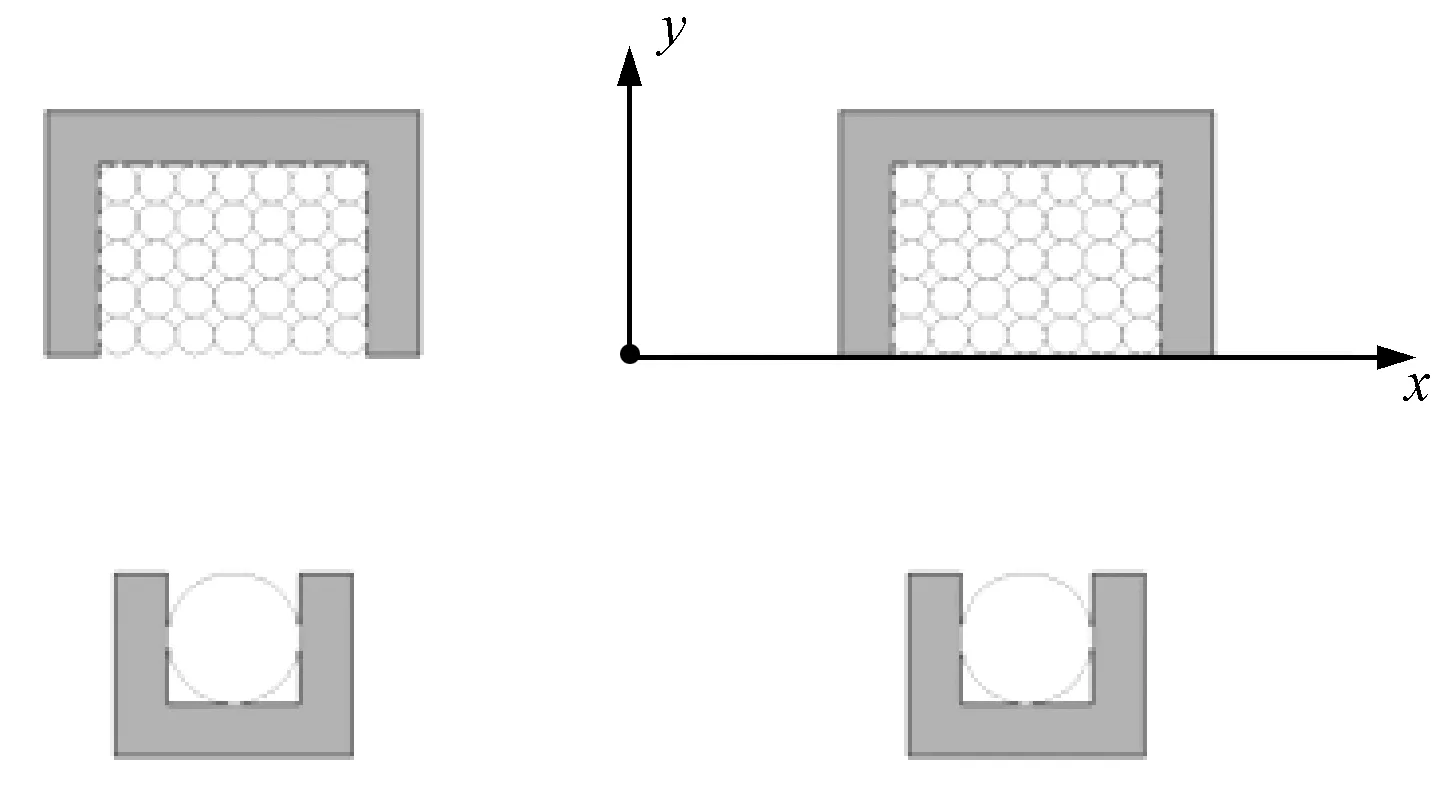
图7 原边带磁心的非接触变压器模型Fig.7 Contactless transformer with primary core

二维计算结果如表1所示。通过在原边绕组周围布置磁心，非接触变压器的原边自感提高了1.8倍，互感提高了79.55%，可见，在原边绕组周围布置磁心能够显著提高耦合性能。

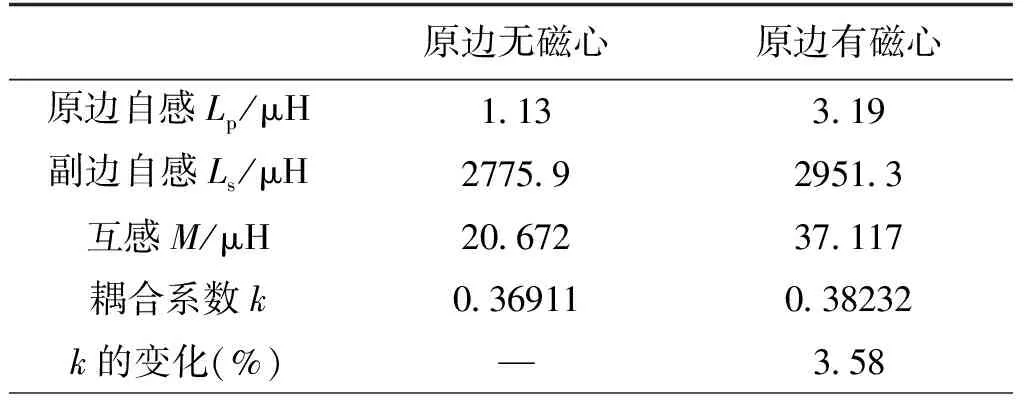
表1 二维计算结果

4.2 副边结构

长度为lm、截面积为Sm的磁通管，其磁阻计算公式为：

(23)

对于如图8所示的U型磁心结构，根据磁路分析，要增大磁心柱与磁心窗口之间的磁阻差，可以将磁心柱往外侧倾斜，形成梯形结构的磁心，增大磁心窗口的长度lm，减小两边磁心柱的长度hm，从而实现耦合性能的提高。

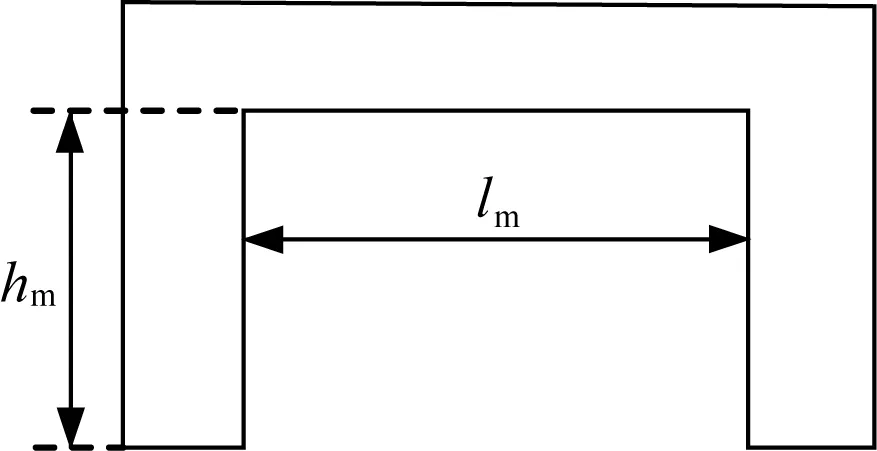
图8 磁心结构优化方法Fig.8 Optimization of core structure

除了磁心形状的改变，不同绕制方式的绕组产生的磁场也遵循相同规律，因此将副边绕组也布置成上窄下宽的形式。根据磁心尺寸的改变，可将副边绕组扁平化布置，以减小多匝导体之间的相互耦合。分别建立优化前后的有限元模型，如图9所示。

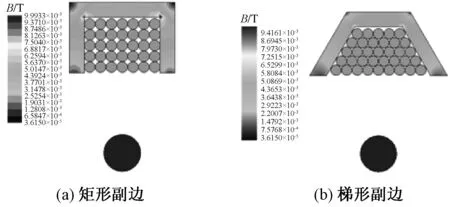
图9 有限元模型Fig.9 FEM Models

两种副边结构的非接触变压器三维计算结果如表2所示。可以看出，优化后的梯形副边结构，副边自感比传统的矩形结构减小了14.89%，而互感增大了1.72%，耦合系数提高了10.22%。计算结果验证了磁路分析的正确性。

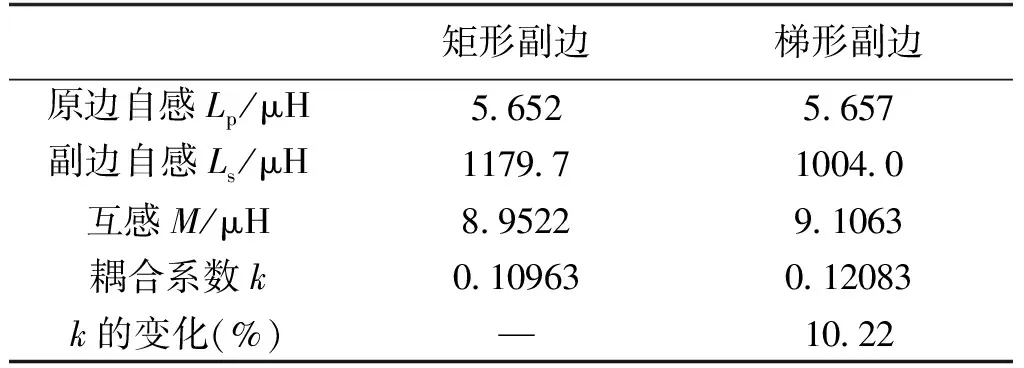
表2 三维计算结果

若不考虑非接触变压器的宽度要求，进一步地，对副边绕组的布置方式进行优化，取副边绕组匝数为35匝，对比三种副边绕组布置方式，分别为：① 5×7；②12+10+7+6；③13+12+10。相应地，三组的磁心宽度递增，如图10所示。对应的耦合系数如表3所示。

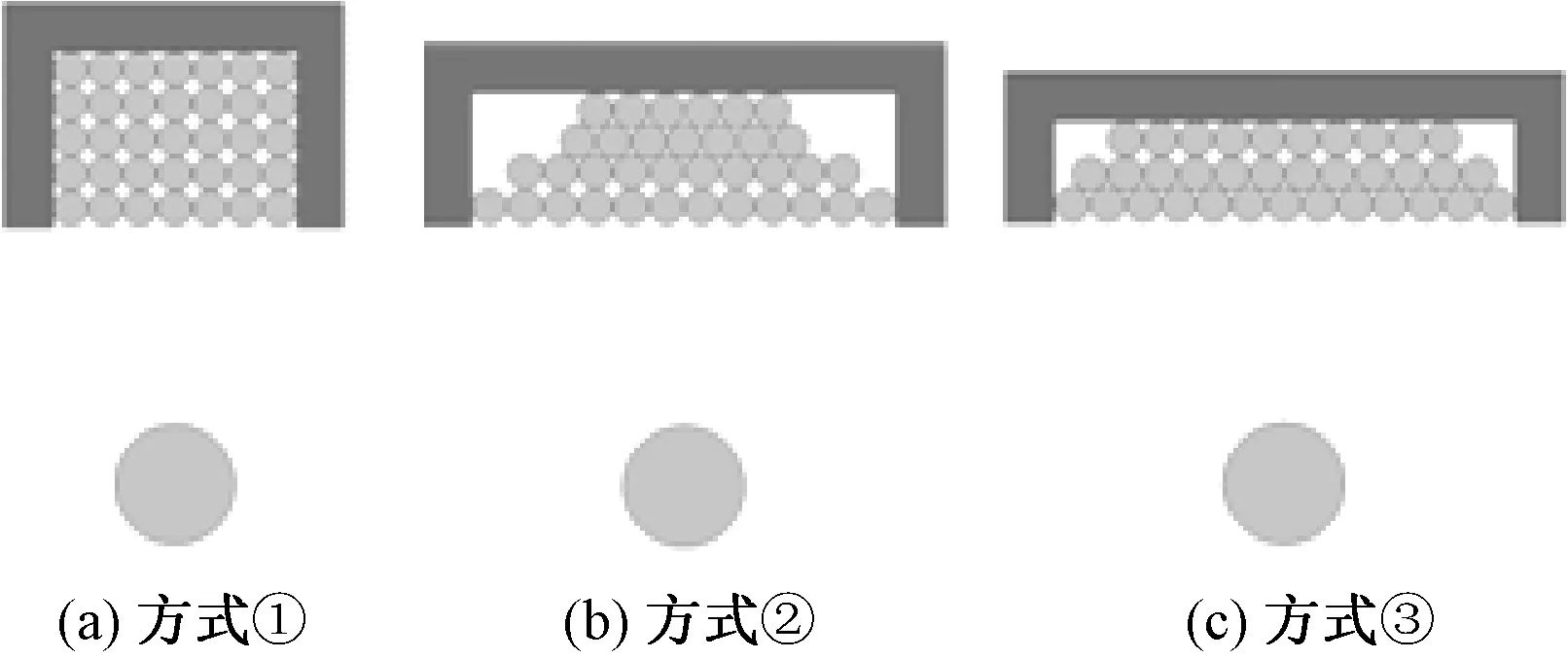
图10 三种副边绕组布置方式Fig.10 Three types of secondary winding arrangement

绕组布置方式①②③k036882043613044975

从计算结果可以看出，将副边绕组排列成截面为梯形的形式，并相应地调整U型磁心的尺寸，能够增大非接触变压器的耦合系数，证明了优化方法的正确性。

同时，当非接触变压器所加激励相等时，三种副边绕组布置方式对应的U型磁心顶部磁场强度分布如图11所示。可以看出，三种方式中，磁心中的磁场强度①>②>③，表明当增大非接触变压器的原、副边电流，副边绕组截面为矩形的方式①的磁心会先达到饱和，而绕组截面为梯形的扁平化排布的方式③能够承受更大的电流，适合应用于大功率供电场合。

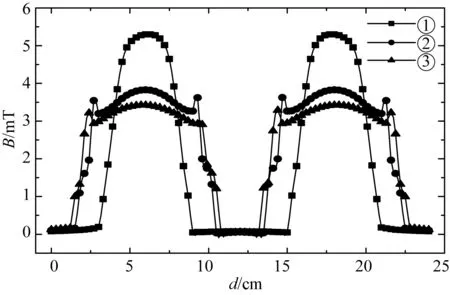
图11 U型磁心顶部磁场强度分布Fig.11 Magnetic field strength at top of U core

根据第3节的分析，原、副边绕组之间的空气隙处的磁通为漏磁通。图12为副边绕组下方5mm的气隙中，三种副边绕组布置方式对应的磁场强度分布。方式③的副边绕组正下方磁场强度最小，表明原、副边之间的漏磁最小。

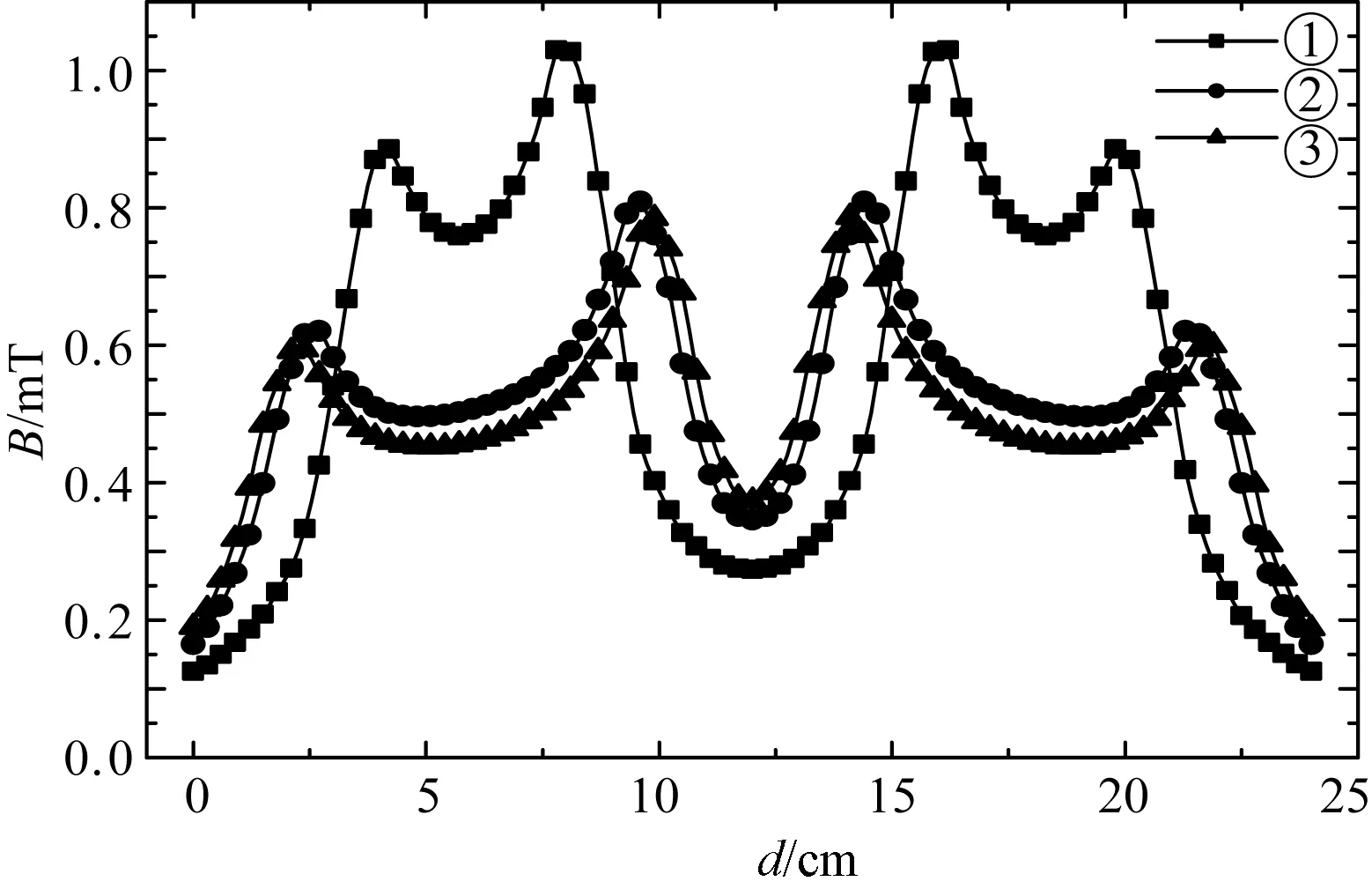
图12 副边绕组下方5mm处磁场强度分布Fig.12 Magnetic field strength at 5mm below the secondary windings

综上所述，梯形截面的绕组布置方式相比于矩形截面的绕组布置方式能够增大非接触变压器的耦合系数，并减少漏磁，这证明了优化方法的有效性。

5 实验验证

为了验证改进后的梯形绕组截面非接触变压器的整体性能，综合考虑输出功率要求、非接触变压器体积等因素，制作非接触变压器样机。根据系统的要求，非接触变压器原边绕组为2匝，副边每个接收线圈34匝，绕制方式为10+9+8+7共4层。为了获得较大的输出功率，样机采用4个结构和参数相同的接收线圈并联输出的形式，对其中一个进行实验测量电感参数，实验平台如图13所示。测量得到的系统电路参数如表4所示。

图13 实验平台Fig.13 Experimental platform

测量得到电感参数与有限元仿真结果基本一致，并且梯形副边绕组截面的结构具有良好的耦合性能，耦合系数达到0.45。

图14为非接触变压器原边电压和原边电流的实验波形。可以看出，经过原边电容的补偿，原边绕组两端的电压和绕组电流同相。原边绕组两端电压基波有效值约为226V，原边电流有效值为146A，非接触变压器原边输入功率约为32.98kW，副边负载消耗功率约为28.12kW，效率达到85.3%，满足系统要求。

表4 IPT系统电路参数Tab.4 Design specifications and circuit parameters of prototype for IPT system

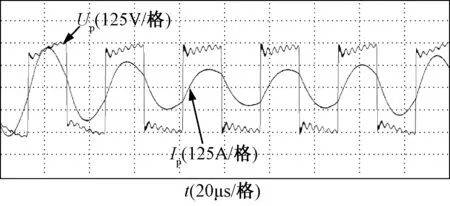
图14 原边电压和原边电流Fig.14 Primary voltage and primary current

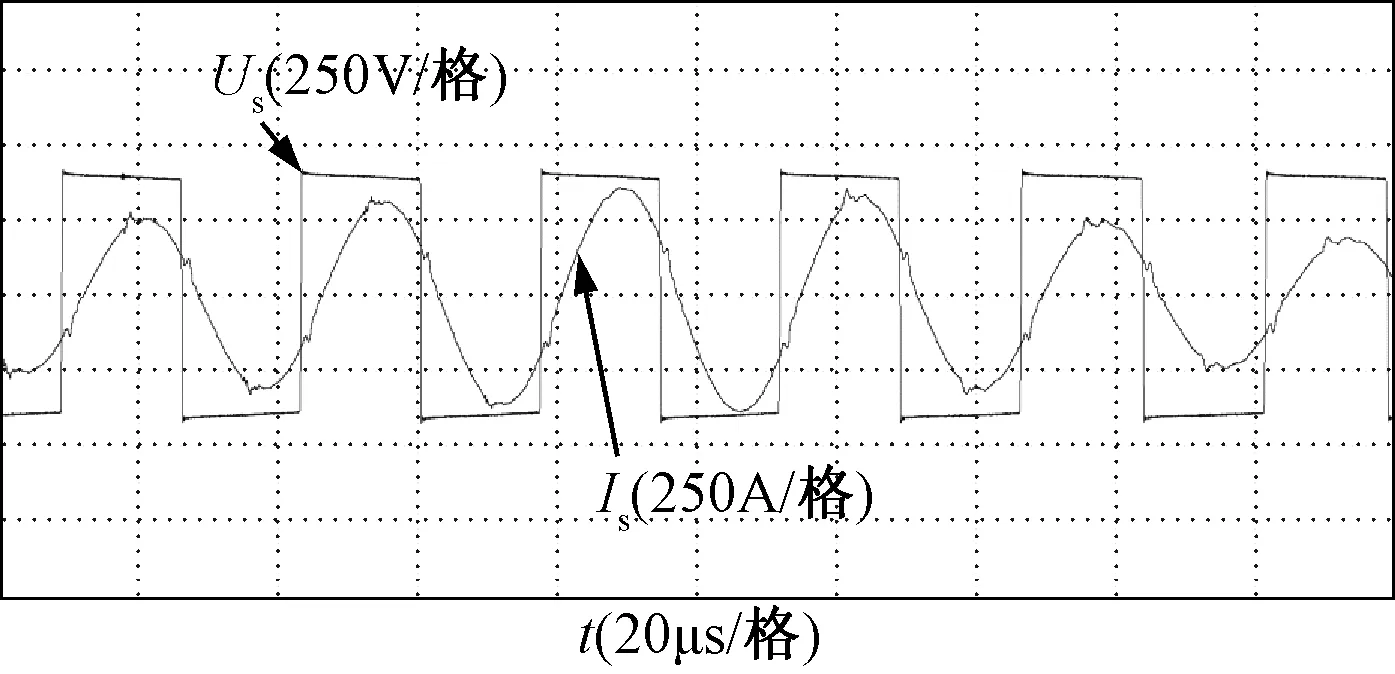
图15 副边电压和副边电流Fig.15 Secondary voltage and secondary current

6 结论

本文分析了U型磁心非接触变压器的磁路结构，并对结构进行优化，以提高耦合系数。由于非接触变压器的原、副边结构不对称，将磁场拆分成副边开路和原边开路两种情况下分别考虑。根据有限元电磁场仿真结果，分别建立了副边开路和原边开路时的等效磁路，并推导出电感及耦合系数关于磁阻的表达式。基于此，通过一定的简化，定性给出了磁路结构的优化方向。有限元计算结果证明了磁路模型及优化方法的正确性。根据磁路模型，提出了非接触变压器的绕组梯形布置的优化方案，并制作实验样机。实验结果显示，在48mm气隙下，优化后的非接触变压器耦合系数达到0.45，系统效率达到85.3%。

[1] 周雯琪(Zhou Wenqi)．感应耦合电能传输系统的特性与设计研究(Research on characteristic and design of inductively coupled power transfer system) [D]．杭州：浙江大学(Hangzhou: Zhejiang University)，2008．

[2] 杨庆新，陈海燕，徐桂芝，等(Yang Qingxin，Chen Haiyan，Xu Guizhi，et al.)．无接触电能传输技术的研究进展(Research progress in contactless power transmission technology) [J]．电工技术学报(Transactions of China Electrotechnical Society)，2010，25(7)：6-13．

[3] Cheng Z，Lei Y，Song K，et al．Design and loss analysis of loosely coupled transformer for an underwater high-power inductive power transfer system [J]．IEEE Transactions on Magnetics, 2015，51(7)：1-10.

[4] Hu C H，Chen C M，Shiao Y S, et al．Development of a universal contactless charger for handheld devices [A]．IEEE International Symposium on Industrial Electronics[C]．2008. 99-104.

[5] 李建贵(Li Jiangui)．无接触电能传输系统可分离变压器性能研究(The performance study of detachable transformer based on contactless energy transmission system) [D]．天津：河北工业大学(Tianjin: Heibei University of Technology), 2007.

[6] Adeel Z，Covic A.，Dariusz K．A bipolar pad in a 10-kHz 300-W distributed IPT system for AGV applications [J]．IEEE Transactions on Industrial Electronics, 2014，61(7)：3288-3301.

[7] 马纪梅，杨庆新，陈海燕(Ma Jimei，Yang Qingxin，Chen Haiyan)．影响无接触供电系统效率的因素分析(Analysis on affecting factors of efficiency of the contactless energy transmission system) [J]．电工技术学报(Transactions of China Electrotechnical Society), 2010，25(7)：19-23.

[8] 李明硕，陈乾宏，侯佳，等(Li Mingshuo，Chen Qianhong，Hou Jia，et al.)．一种具有聚磁作用的轨道式非接触变压器(A new type of contactless transformer in track inductive power transfer system) [J]．电工技术学报(Transactions of China Electrotechnical Society), 2013，28(10)：25-32．

[9] 周雯琪，马皓，何湘宁(Zhou Wenqi，Ma Hao，He Xiangning)．感应耦合电能传输系统不同补偿拓扑的研究(Investigation on different compensation topologies in inductively coupled power transfer system) [J]．电工技术学报(Transactions of China Electrotechnical Society)，2009, 24(1)：133-140.

[10] 程鹏天，王健强，杜秀(Cheng Pengtian，Wang Jianqiang，Du Xiu)．电动汽车感应耦合充电系统一种新型拓扑的研究(Investigation of a novel topology for inductively coupled charging system in electric vehicles) [J]．电工技术学报(Transactions of China Electrotechnical Society), 2013，28(2):86-91.

[11] 程志远，朱春波(Cheng zhiyuan，Zhu Chunbo)．非接触式大功率感应充电系统谐振变换器的设计(Design of the resonant converter for the contactless inductive charging system) [J]．电工技术学报(Transactions of China Electrotechnical Society), 2013，28(1)：404-408．

[12] Tobias D，Rikw D D. A dual-side controlled inductive power transfer system optimized for large coupling factor variations and partial load [J]．IEEE Transactions on Power Electronics, 2015，30(11)：6320-6328.

[13] Wang C S，Covic G A，Stielau O H．Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems [J]．IEEE Transactions on Industrial Electronics, 2004，51(1)：148-157.

[14] Mahshid A，Anand B，Hamid A T．High-frequency AC-link PV inverter [J]. IEEE Transactions on Industrial Electronics，2014，61(1)：281-291.

[15] Daniel T，Lee C G，Park J H．High-order resonant converter topology with extremely low-coupling contactless transformers [J]．IEEE Transactions on Power Electronics, 2016，31(3)：2347-2361.

[16] 夏晨阳，贾娜，庄裕海(Xia Chenyang，Jia Na，Zhuang Yuhai)．U型磁芯结构ICPT系统功率传输容量研究(Power capacity analysis of ICPT system based on U-magnetic core circuit) [J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014，33(8):7-10.

[17] 张巍，陈乾宏，Wong S C，等(Zhang Wei，Chen Qianhong，Wong S C，et al.)．新型非接触变压器的磁路模型及其优化(Reluctance circuit and optimization of a novel contactless transformer) [J]．中国电机工程学报(Proceedings of the CSEE), 2010，30(27)：108-116.

[18] Min L，Drazen D，Jost A．Leakage flux modelling of multi-winding transformer using permeance magnetic circuit [A]．IEEE Applied Power Electronics Conference and Exposition (APEC) [C]．2016. 1108-1114.

[19] Hsu C H，Liu C H，Hsiao Y C，et．al．High frequency characteristics of magnetostriction on vibration and noise for single-phase transformer dependence of magnetic circuit method [A]．International Symposium on Computer，Consumer and Control [C]．2014. 399-402.

[20] 孙跃，李云涛，叶兆虹，等(Sun Yue，Li Yuntao，Ye Zhaohong，et al.)．三线圈ICPT系统中继线圈的位置优化(Optimization for relay coil of 3-coil inductively coupled power transfer system) [J]．电工技术学报(Transactions of China Electrotechnical Society), 2016，31(13)：164-171.