全SiC三相逆变器传导电磁干扰建模与预测

段卓琳， 范 涛， 张 栋， 温旭辉

(1. 中国科学院电工研究所， 北京 100190; 2. 中国科学院大学， 北京 100049; 3. 中国科学院电力电子与电力传动重点实验室， 北京 100190; 4. 北京电动车辆协同创新中心， 北京 100190)

1 引言

电力电子器件是电力电子装置的重要基础。Si 功率器件经过五十多年的长足发展，其性能已趋近理论极限，难以再大幅度提升[1]。近年来，以SiC 为代表的宽禁带半导体技术发展迅速。与 Si 器件相比，SiC器件具有阻断电压高、通态电阻低、开关损耗小且能耐高温工作的特点，能够大幅降低装置的功耗、缩小装置的体积，特别在高温、高频和大功率的应用领域，显示出 Si器件难以比拟的巨大应用优势和潜力，因此在三相逆变器系统中具有良好的应用前景[2]。

在三相逆变器系统中，功率开关器件的快速开通、关断使得电压和电流在短时间内发生瞬变，产生高的 du/dt和di/dt，形成很强的电磁干扰(ElectroMagnetic Interference , EMI)，对系统的安全性和可靠性造成威胁。对于全SiC逆变器，更快的开关速度，更高的开关频率，导致了更强的EMI。在设计阶段对逆变器的电磁干扰进行预测，可以节约成本，缩短设计周期[3]。通常，系统的EMI预测方法可以分为频域法和时域法两种。频域法通过建立系统的EMI等效模型进行噪声预测[4]，可以快速得到系统的噪声频谱分布，但模型的电路意义不够直观。时域方法简单直接[5,6]，但对计算机性能的要求较高。随着计算机性能的提高，时域仿真方法在预测EMI方面得到了越来越多的应用。

本文所要分析的全SiC三相逆变器及其测试装置的结构图如图1所示。直流电源连接线路阻抗稳定网络(line impedance stabilization network，LISN)后，连接逆变器，再连接三相电感负载。其中逆变器所采用的开关模块是Cree公司型号为CAS300M12BM2的300A/1200V的SiC MOSFET开关模块。

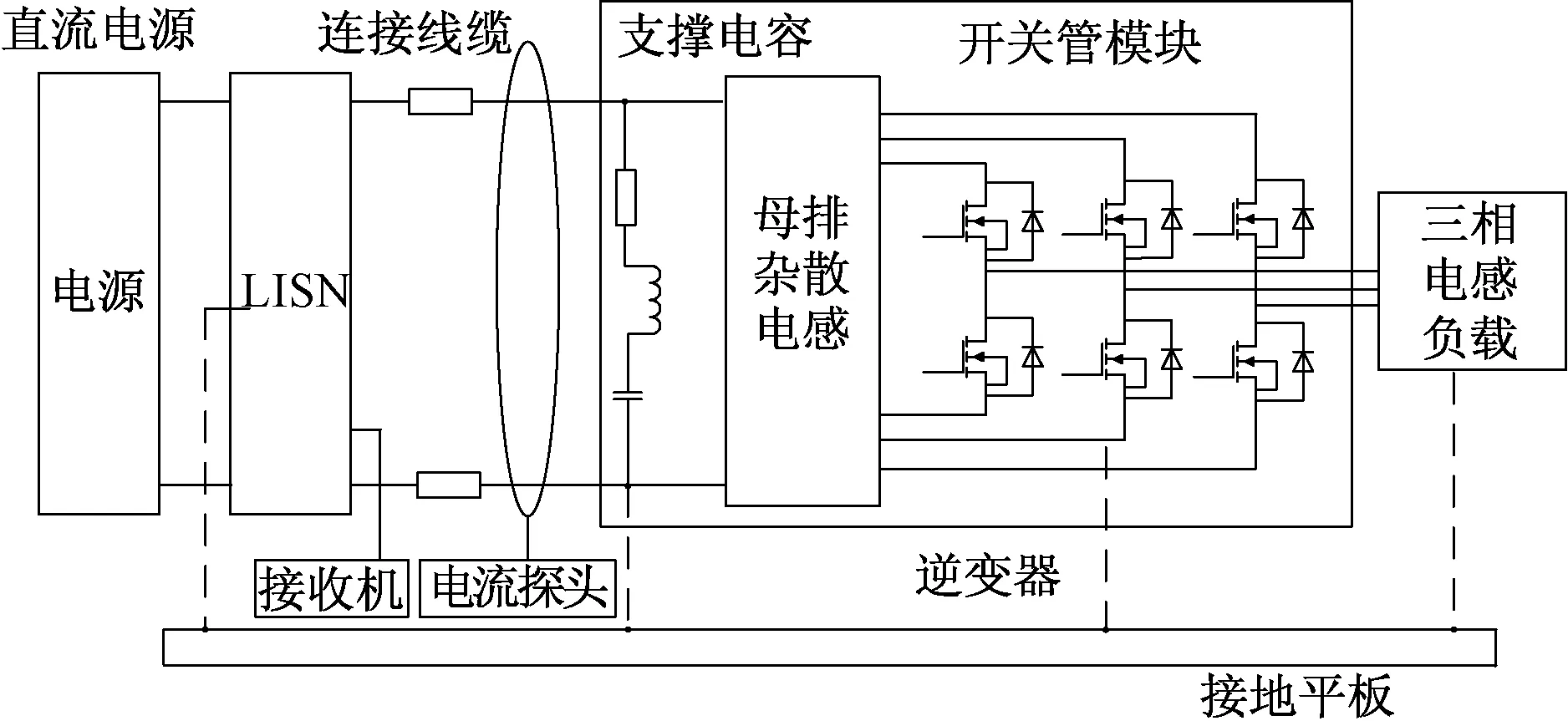
图1 测试装置结构图Fig.1 Diagram of test equipments

本文首先建立了系统干扰源及各个部件的模型，再通过时域仿真加快速傅里叶变换(Fast Fourier Transform, FFT)的方法，对电源端口处的干扰频谱进行了预测，并与接收机实测结果进行了对比，验证了模型的正确性。

2 时域仿真建模方法

2.1 开关管建模及验证

本文采用Spice语言建立了开关管的行为模型，其结构如图2所示，主要包含静态模型、极间电容模型以及模块杂散电感等。

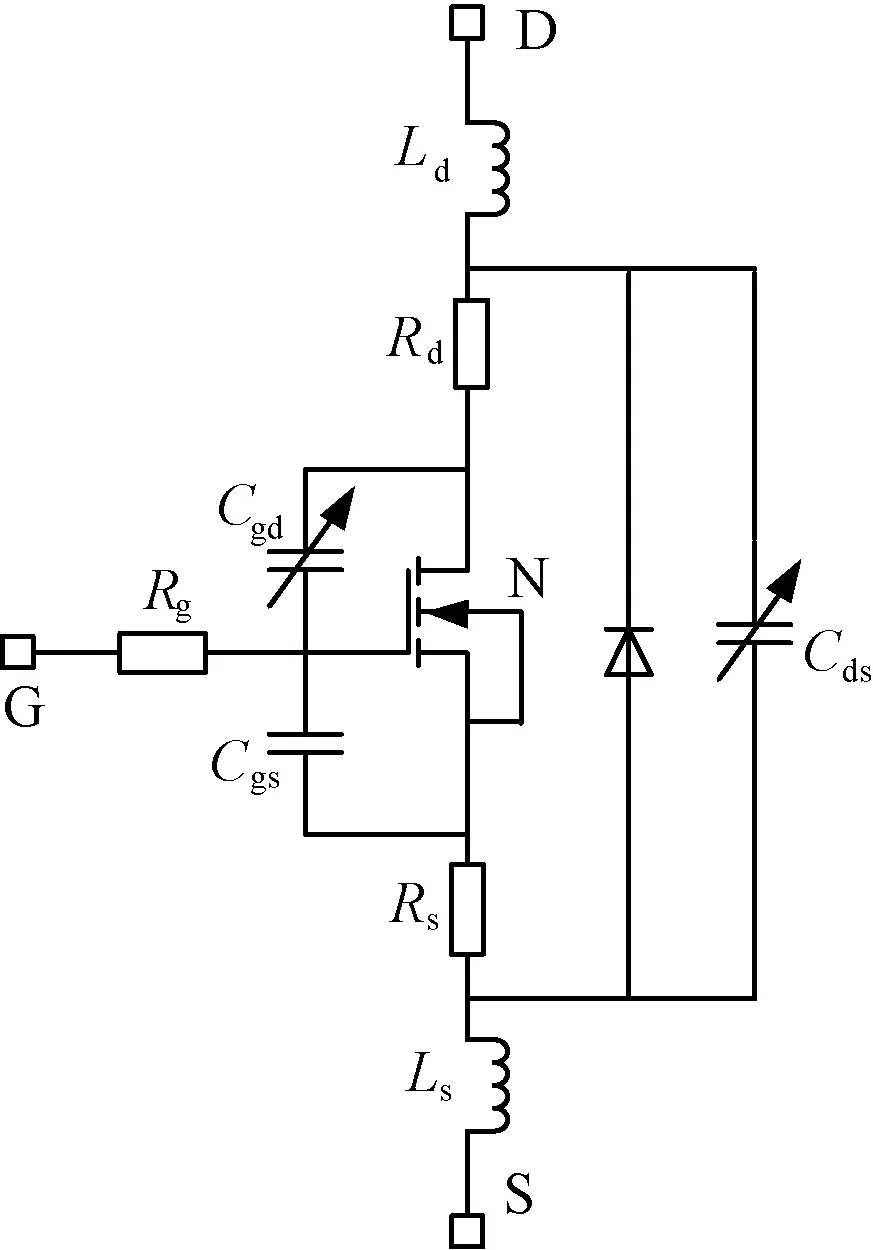
图2 开关管行为模型结构图Fig.2 Behavior model of switching transistor

图2中，Rd、Rs分别为漏、源极电阻，Ld、Ls分别为漏、源极杂散电感，Rg为内部栅极电阻，Cgs、Cgd、Cds为极间电容。MOSFET的静态特性采用Shichman-Hodges模型[7]，漏极电流Id根据截止区(VgsVgs-Vth) 可以写为：

(1)

式中，Vth为器件的阈值电压；Kp为与传输导纳相关的参数；λ为沟道长度调制系数；这些参数可以通过数据手册中的静态特性曲线抽取得到[8]。静态特性曲线仿真结果与数据手册的对比如图3所示。可以看出，静态特性曲线仿真结果与数据手册结果具有良好的一致性。

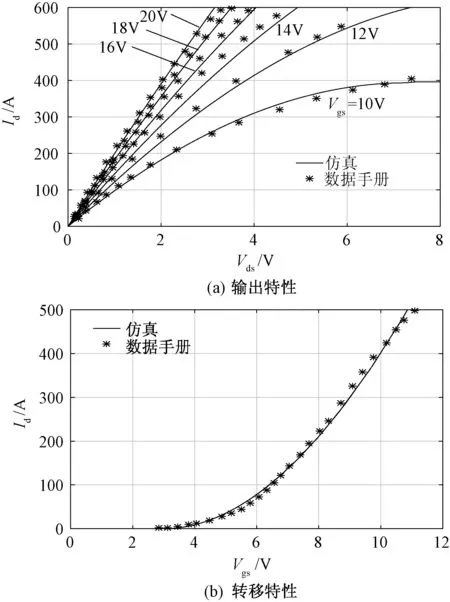
图3 静态特性仿真结果与数据手册对比Fig.3 Comparison of simulated and datasheet static characteristics

为了准确反映开关过程，以下对极间电容进行建模。栅源极间电容Cgs几乎不随电压变化[9,10]，可根据式(2)计算得到。

(2)

式中，Q1为栅荷特性曲线第一阶段的电荷量；Vgs(m)为密勒平台电压。栅漏极电容Cgd随栅漏极电压Vgd变化明显，当Vgd>0时，器件导通，Cgd是氧化层电容，为最大值；当Vgd<0时，器件关断，Cgd为最小值。采用式(3)的经验公式对Cgd进行建模：

(3)

式中，Cgdmax、Cgdmin分别为Cgd的最大值和最小值，可通过LCR表测量得到；Ugd(th)决定了Cgd电容曲线的转折电压点，可通过曲线拟合得到；ΔUgd决定了电容特性曲线最大值与最小值之间的宽度，其值可通过拟合数据手册的Cgd曲线得到。输出电容采用Spice软件自带的模型，其表达式可以写为：

(4)

式中，Vj为自建势垒电压；Cjo为电压为零时输出电容的最大值；m为结的梯度系数，其值取决于PN结两侧的掺杂情况。

最终，极间电容仿真值与数据手册值的对比结果如图4所示。由图4可知，在大部分工作范围内，极间电容仿真值与数据手册值对应效果良好。

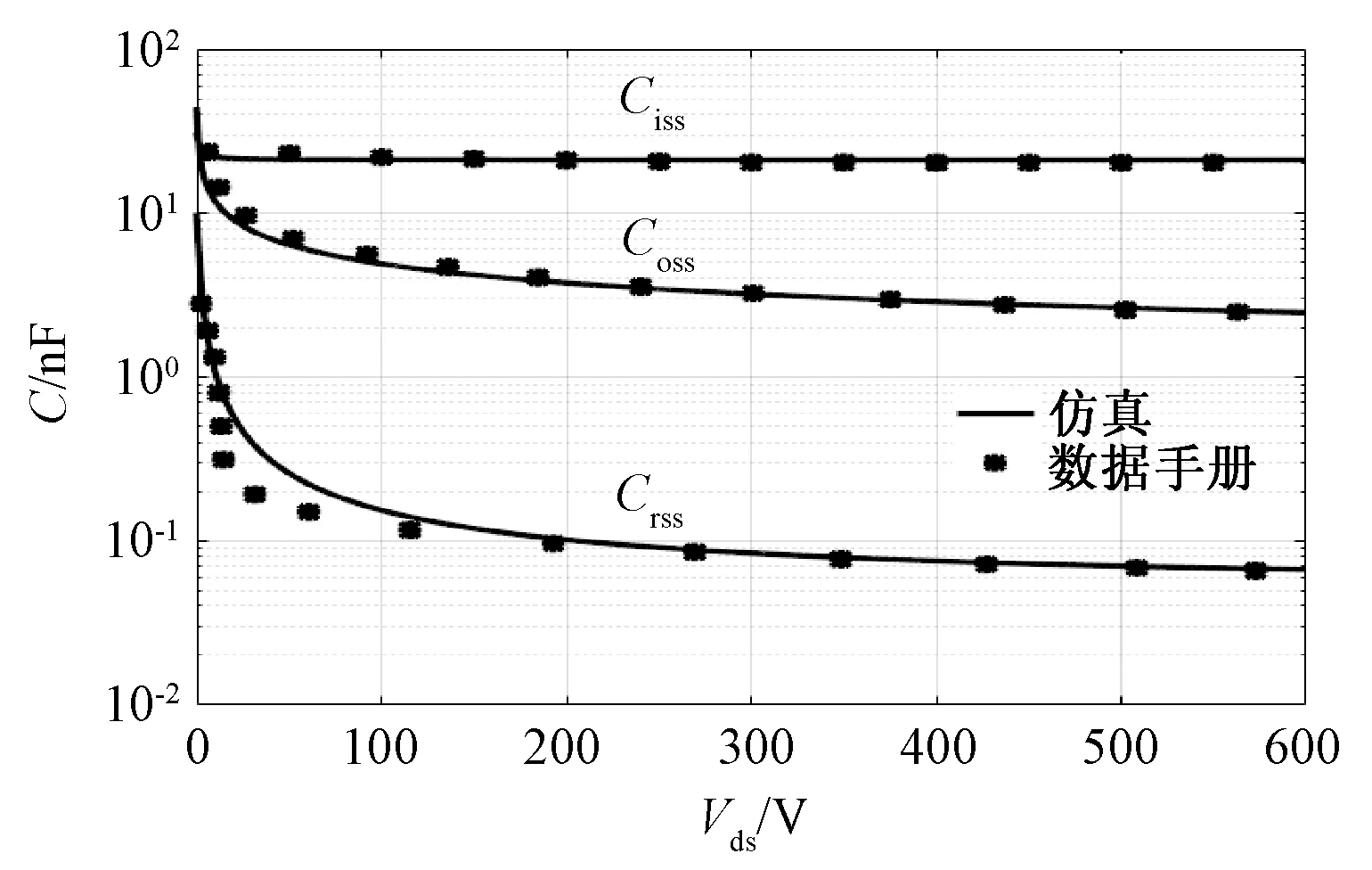
图4 极间电容仿真值与数据手册值对比Fig.4 Comparison of simulated and datasheet interelectrode capacitances

2.2 无源器件及杂散参数建模及验证

(1)负载电感建模

逆变器的负载为三个150μH“Y”型连接的电感，采用安捷伦Agilent E4990A阻抗分析仪对负载的差、共模阻抗进行了测量。差模测量是测量两根线缆短接后与另一根线缆端口处的阻抗，共模测量是测量三根线缆短接后与公共地端口的阻抗[11]。图5(a)为差模阻抗实测值与仿真值的对比。可以看出，在所测频段 (50Hz～30MHz)内，差模阻抗有一个波峰，因此采用并联二阶RLC电路进行拟合，等效电路模型如图5(b)所示。

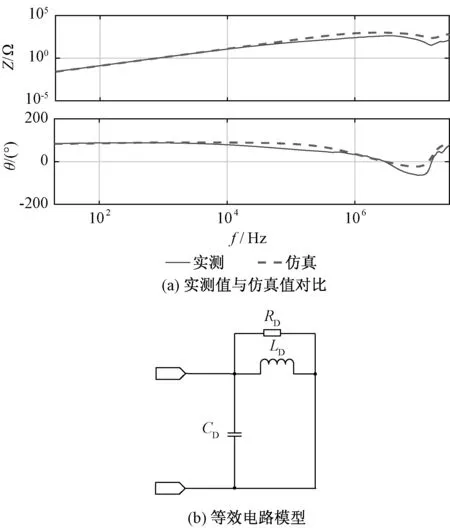
图5 差模阻抗实测值与仿真值对比及等效电路模型Fig.5 Comparison of measured and simulated DM impedances and equivalent model

图5中，RD、LD、CD分别为差模等效电路中的电阻、电感、电容。电感值LD可以根据低频段阻抗计算得到，电容值CD可以根据如式(5)所示的谐振频率值计算得到：

(5)

根据图5(b)中的等效电路可以得到差模阻抗的表达式，如式(6)所示：

(6)

式中，ω=2πf。再根据式(5)，则并联谐振峰值点处的差模阻抗值为：

Zpeak=RD

(7)

由式(7)即可计算得到RD的值。

图6 (a)为共模阻抗实测曲线与仿真曲线的对比。可以看出，在所测频段 (10kHz～30MHz)内，共模阻抗有一个波谷，因此采用串联二阶RLC电路拟合，等效电路如图6 (b)所示。其中，RC、LC、CC分别为共模等效电路中的电阻、电感、电容，电容CC可以根据低频段阻抗值计算得到，电感值LC可根据式(5)由谐振频率值计算得到。

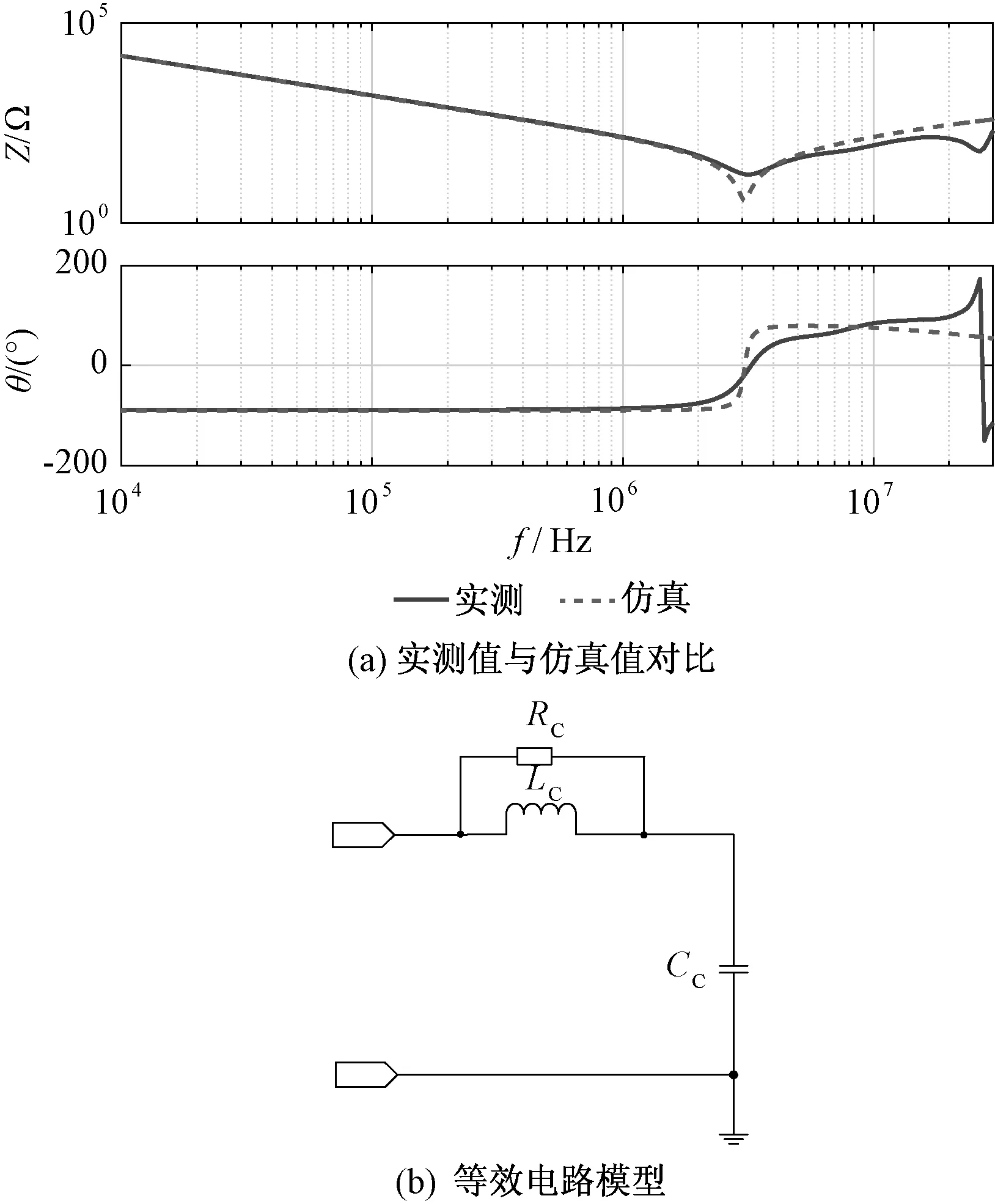
图6 共模阻抗实测值与仿真值对比及等效电路模型Fig.6 Comparison of measured and simulated CM impedances and equivalent model

根据差共模等效电路模型，可以得到三相等效电路模型，如图7所示。

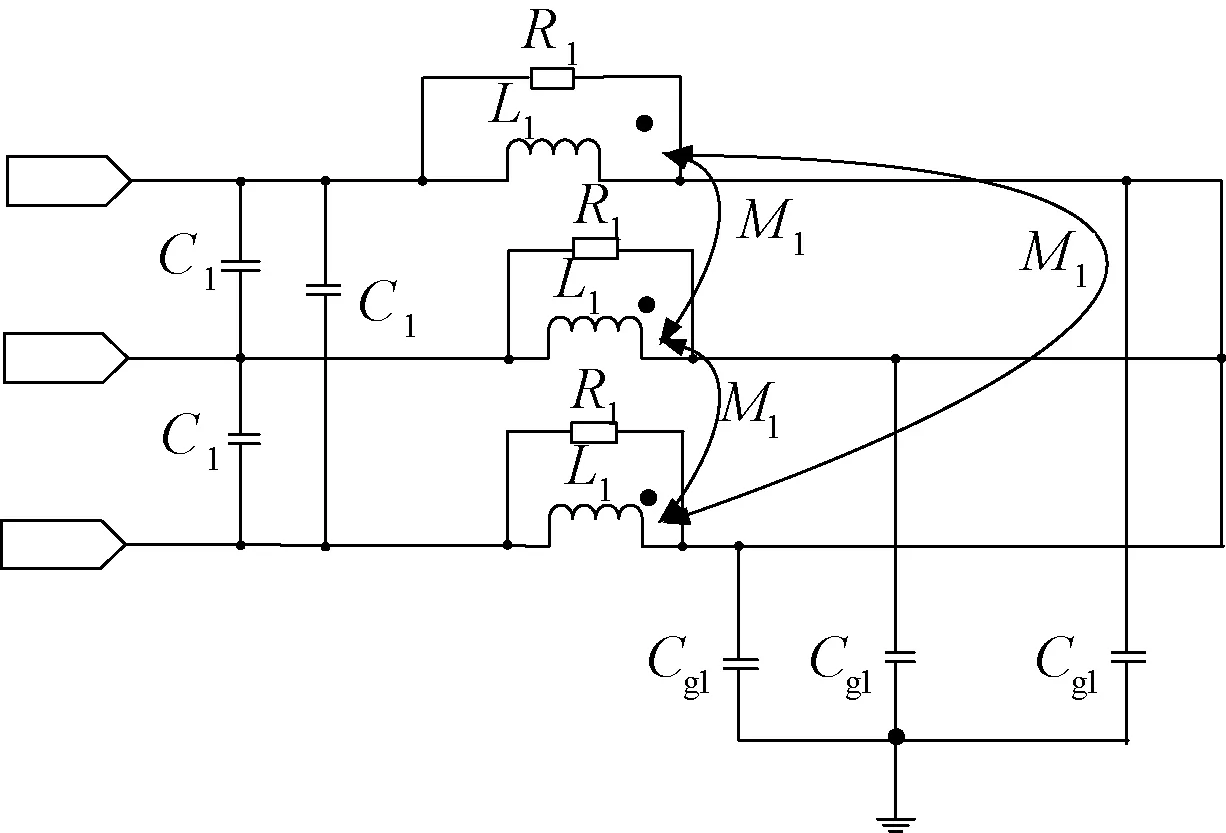
图7 三相等效电路模型Fig.7 Three phase equivalent circuit model

图7中，L1、M1、C1、Cg1、R1分别为三相等效电路的电感、互感、电容、电阻。三相等效电路参数值与差共模电路参数值的关系如式(8)所示：

(8)

根据式(8)，建立并拟合差共模阻抗后，可以计算得到负载等效电路模型中的各个参数值，如表1所示。

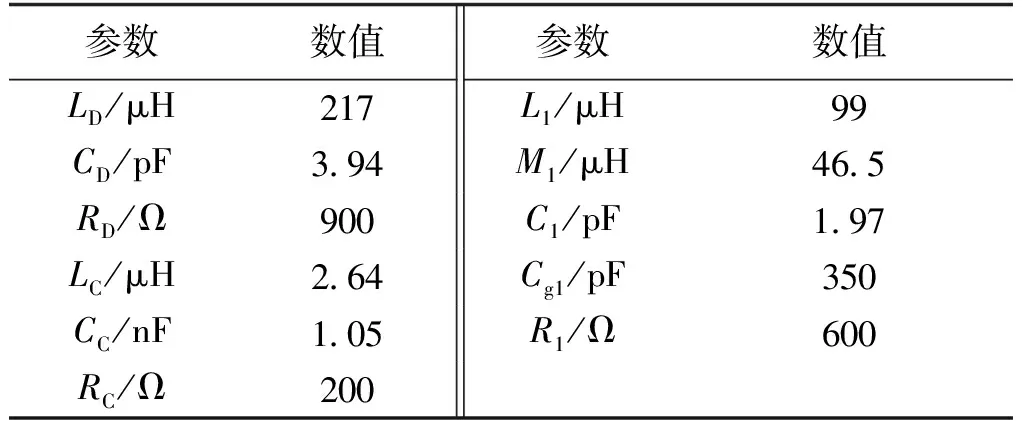
表1 负载等效电路模型中的参数值Tab.1 Parameters in load equivalent circuits

最终由图5(a)、图6(a)中差、共模阻抗仿真值与实测值的对比可以看出，在所测频率范围内，仿真值与实测值对应效果良好。

(2)电容器建模

电容器采用厦门法拉电子公司的塑料薄膜电容器，使用阻抗分析仪测量了电容器的阻抗，其等效电路如图8 (a)所示，仿真值与实测值的对比如图8 (b)所示。由图8 (b)可知，在10kHz～30MHz的频率范围内电容器阻抗仿真值与实测值对应效果良好。

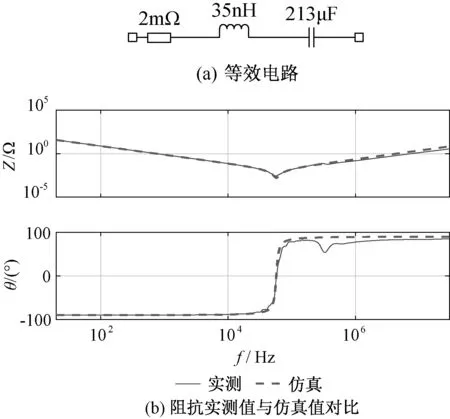
图8 薄膜电容器实测值与仿真值对比及等效电路模型Fig.8 Comparison of measured and simulated film capacitor and equivalent model

(3)LISN及其连接线缆建模

LISN采用Schwarzbeck 的NNLK 8130，其模型可以通过数据手册得到，连接线缆模型可通过阻抗分析仪测试得到。图9(a)为LISN及其连接线缆的等效电路，图9(b)为仿真值与实测值的对比。可以看出，在10kHz～30MHz范围内，LISN及其连接线缆的阻抗仿真值与实测值对应效果良好。

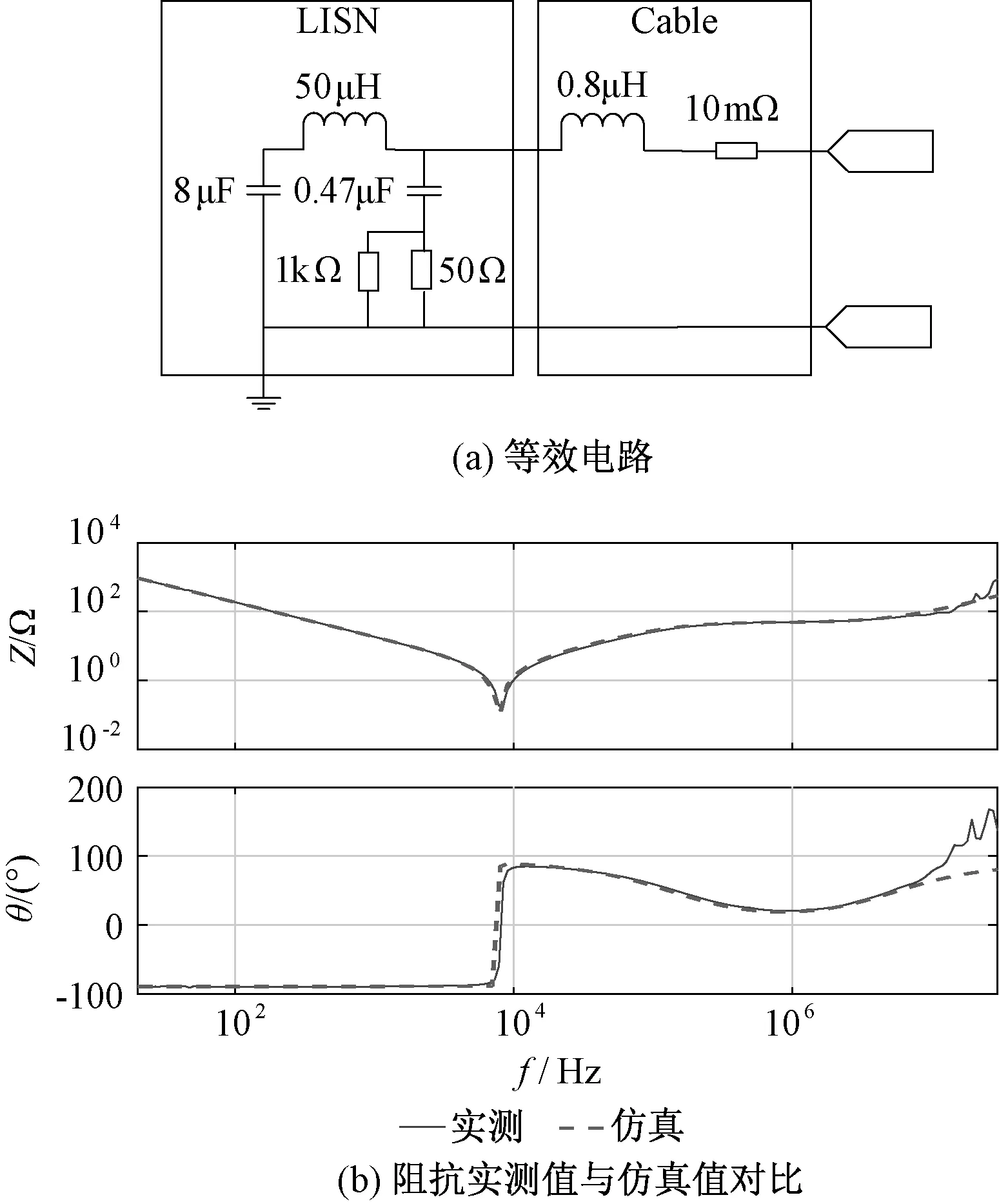
图9 LISN及其连接线缆实测值与仿真值对比及等效电路模型Fig.9 Comparison of measured and simulated LISN and its connected cables and equivalent model

(4)母排杂散电感抽取

图10为母排结构图。其上下层均为铜排，中间为聚对苯二甲酸乙二醇酯(PET)膜。由于磁路耦合、趋肤效应以及邻近效应，母排杂散参数复杂，不能直接计算得到。本文采用有限元工具Ansys Q3D软件抽取母排杂散电感参数。该软件基于矩量法，得到部分元件等效电路的杂散参数，直接以子电路的形式参与电路仿真[12]。

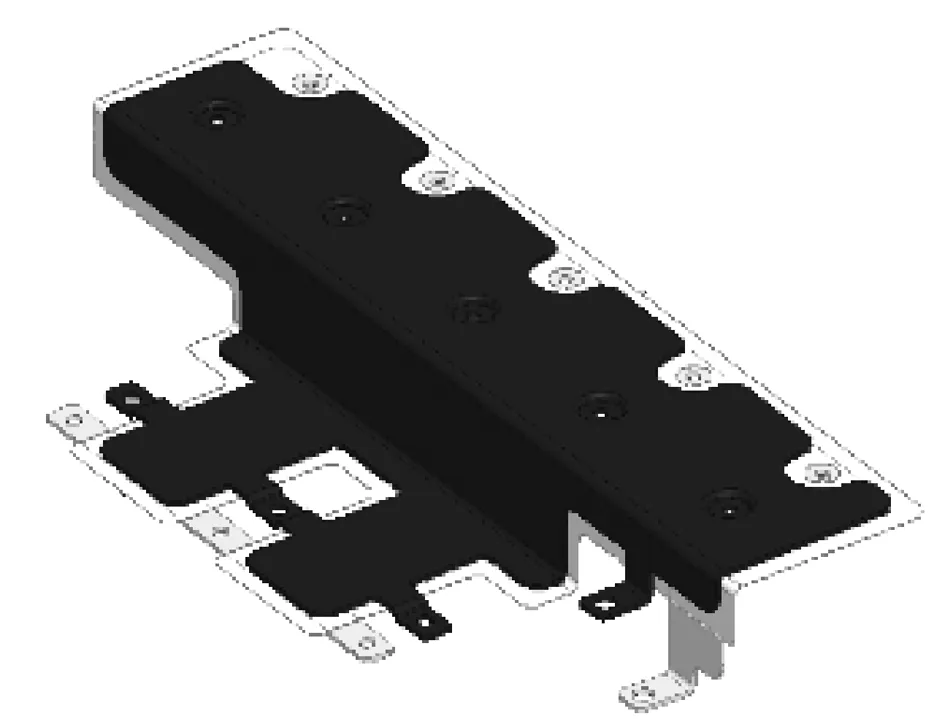
图10 母排结构图Fig.10 Busbar structure

表2为抽取所得到的母排杂散电感参数值。其中，1P、2P、3P为三相的正端子，1N、2N、3N为三相的负端子。

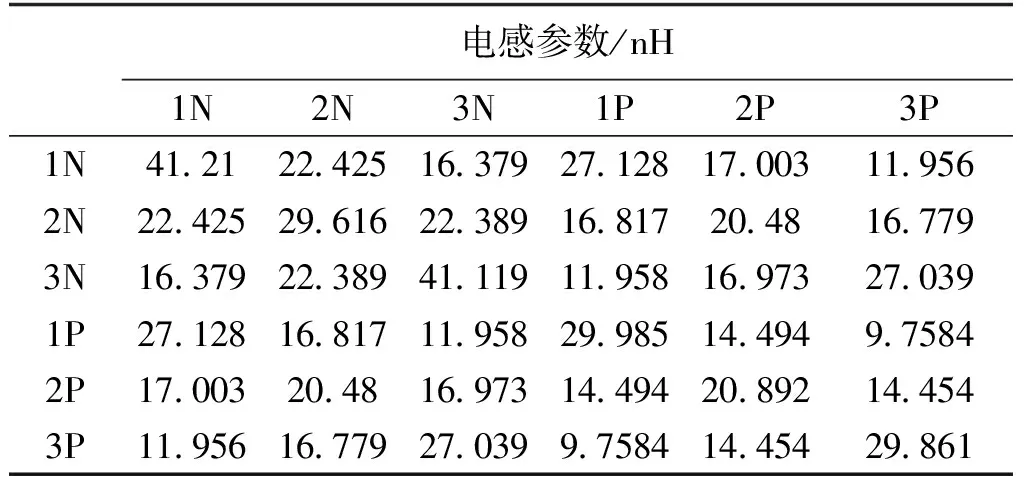
表2 抽取所得到的母排杂散电感参数值Tab.2 Extracted parasitic inductances of the busbar

(5)对地杂散电容测量

由于器件的输出电容相比对地杂散电容要大得多，故不能测量得到模块各端子对地的杂散电容。为此，将半桥模块三个端子连接在一起，测试模块各端子总的对地电容，如图11所示。

图11 模块对地杂散电容测试方法Fig.11 Test method for switching module to ground stray capacitances

得到开关管对地杂散电容值后，再均分为二，作为半桥模块中每个器件的漏极对地杂散电容。

3 时域仿真与实验结果对比

测试装置的实验布置图如图12所示。其中，LISN采用Schwarzbeck 的NNLK 8130，电流探头采用A.H.公司的BCP-620(带宽为10kHz～500MHz)。接收机采用Rohde&Schwarzbeck ESL3，其频率测量范围为9kHz～3GHz，连接10dB衰减器。

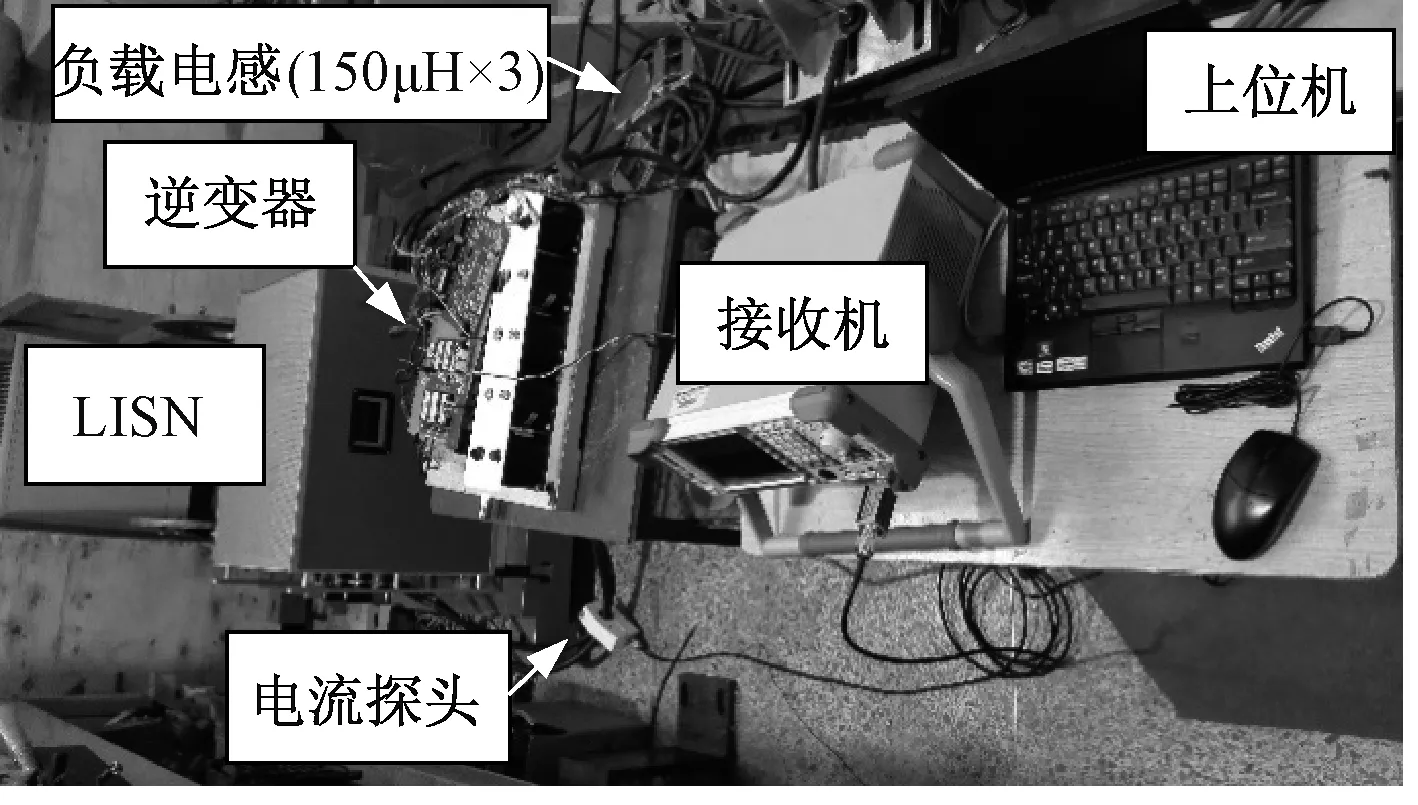
图12 测试装置实验布置图Fig.12 Experimental layout of test equipment

实验采用SVPWM调制策略，开环控制方式，直流母线电压为100V，在程序中设置基波频率及调制比，此时测得的电流峰值为65A，开关频率设置为7.5kHz，系统运行条件如表3所示。

表3 系统运行条件Tab.3 System operating conditions

当直流母线电压升高时，干扰增强。负载电感减小，相同电压下电流增大，干扰增强。当开关频率提高时，干扰增强。

在LISN与逆变器连接侧通过电流探头测试差共模电流噪声。共模电流的测量方式如图13(a)所示，正负线同时穿过电流探头，差模电流方向相反，彼此抵消，共模电流方向相同，测量结果为2iCM。差模噪声的测量方式如图13(b)所示，正负线中一根直接穿过探头，另一根绕制后再穿过探头，共模电流方向相反，彼此抵消，差模电流方向相同，测量结果为2iDM[13]。

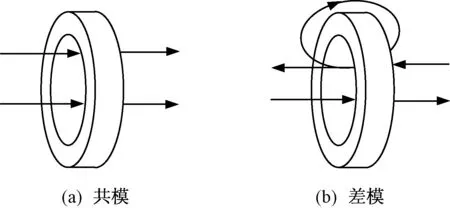
图13 电流探头噪声测量方式Fig.13 Noise measurement methods by current probe

根据本文的建模方法，建立时域仿真电路，采用电路仿真软件LTspice进行仿真。得到LISN侧差、共模干扰电流后，通过FFT即可得到其频谱。

为了将仿真结果与实验结果进行对比，采用接收机模拟算法对仿真结果进行了处理，EMI接收机的工作流程如图14所示。

图14 EMI接收机工作流程图Fig.14 Workflow chart of EMI receiver

频率预选设置为10kHz～30MHz，经过混频处理，再经6dB带宽为9kHz的中频滤波器滤波。中频滤波器采用高斯近似滤波器，它是一种根据近似高斯函数的形状来选择权值的线性平滑的滤波器，中频滤波器的幅值可以写为[14]：

|GIF(f,fIF)|=e-(f-fIF)2/c2

(9)

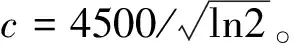
图15 仿真接收机与实测接收机差共模频谱对比Fig.15 Comparison of simulated and measured DM and CM noises

4 结论

本文以全SiC电机驱动系统的逆变器为研究对象，建立了其各部件的传导干扰模型，采用仿真软件对差共模传导干扰进行了预测，并与实验测试结果进行了对比。

(1)对MOSFET及其反并联二极管进行了行为特性建模，静态特性及动态特性与数据手册结果对应良好。

(2)采用阻抗分析仪测试了负载电感、电容器、LISN及连接线缆的阻抗，采用谐振单元法拟合得到了负载电感阻抗的等效模型，建立了电容器，LISN及连接线缆的仿真模型，采用有限元软件提取了母排杂散电感参数，传播路径阻抗的建模结果与实测结果较为一致。

(3)仿真EMI噪声与实测结果的对比表明，在10kHz～30MHz的频率范围内，误差在6dB范围内。

[1] 钱照明，盛况 (Qian Zhaoming, Sheng Kuang).大功率半导体器件的发展与展望 (Development and perspective of high power semiconductor device)[J]．大功率变流技术(Converter Technology & Electric Traction), 2010, (1): 1-9.

[2] 钟志远，秦海鸿，袁媛，等(Zhong Zhiyuan, Qin Haihong, Yuan Yuan, et al.). 碳化硅 MOSFET桥臂电路串扰抑制方法(SiC MOSFET bridge arm crosstalk suppression method)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(5): 8-12.

[3] Lai J, Huang X, Pepa E, et al. Inverter EMI modeling and simulation methodologies[J]. IEEE Transactions on Power Electronics, 2006, 53(3):736-744.

[4] Lu H, Guru A. Modeling conducted emissions in servo drives [A]. IEEE Conferences on Industrial Electronics and Applications (ICIEA) [C]. Melbourne, Australia. 2013. 999-1004.

[5] Ran L, Gokani S, Clare J, et al. Conducted electromagnetic emissions in induction motor drive systems-Part I: Time domain analysis and identification of dominant modes[J]. IEEE Transactions on Power Electronics, 1998, 13(4):757-767.

[6] Zhu H, Lai J, Hefner A. R, et al. Modeling based examination of conducted EMI emission from hard and soft-switching PWM inverters [J]. IEEE Transactions on Industry Applications, 2001, 37(5): 1383-1393.

[7] Shichman H, Hodges D A. Modeling and simulation of insulated-gate field-effect transistor switching circuits [J]. IEEE Journal of Solid-State Circuits, 1968, 3(3):285-289.

[8] McNutt T, Hefner A, Mantooth A, et al. Silicon carbide power MOSFET model and parameter extraction sequence[A]. Power Electronics Specialist Conference[C]. Acapulco, Mexico, 2003. 217-226.

[9] Ren Y, Xu M, Zhou J, et al. Analytical loss model of power MOSFET[J]. IEEE Transactions on Power Electronics, 2006, 21(2):310-319.

[10] Zhou B, Chen Z, Wang S. An improved simulation model for power MOSFET[A]. IEEE Region 10 International Conference on Microelectronics and VLSI[C]. Hong Kong, China, 1995. 436-439.

[11] Sun J, Xing L. Parameterization of three-phase electric machine models for EMI simulation[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 36-41.

[12] Martin C, Schanen J L, Clavel E. Power integration: Electrical analysis of new emerging package[A]. European Conference on Power Electronics and Applications [C]. Toulouse, France, 2003. 7340-7346.

[13] Zhao D, Ferreira J A, Polinder H, et al. Investigation of EMI noise transfer characteristic of variable speed drive system[A]. International Symposium on Power Electronics, Electrical Drives, Automation and Motion[C]. Taormina-Sicily, Italy, 2006. 603-608.

[14] Wang Z, Wang S, Kong P, et al. DM EMI noise prediction for constant on-time, critical mode power factor correction converters[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3150-3157.