等温线和绝热线不能相交于两点的两种证法*

卢晓凤 毛予廷

(西南大学物理科学与技术学院 重庆 400715)

在热学部分我们学习了热力学第零定律、第一定律及第二定律这三大定律之后，发现用其可以解决很多有关热现象的问题，但它也有其局限性．如单纯地用热力学第一定律不能回答的问题有3个，其中第一个是：理想气体的pV图上，等温线和绝热线不能有两个和两个以上的交点．对上述问题的证明我们采用反证法，得出其违反热力学第二定律证明的，其实还可以有其他证法，为此本文就这一问题用两种方法进行证明．

1 证明方法一

命题：论证理想气体绝热线与等温线不能相交于两点．

假设绝热线与等温线相交于A,B两点．

如图1所示，若一条绝热线与一条等温线相交于A,B两点，沿绝热线从A到B,再沿等温线从B到A,于是构成了一个闭合循环，它从单一热源吸热对外做功(等于环路面积)．这违反热力学第二定律，所以是不可能的．

如图1所示，等温线与绝热线构成一个闭合循环系统，则有ΔU=0(因为内能是个态函数).

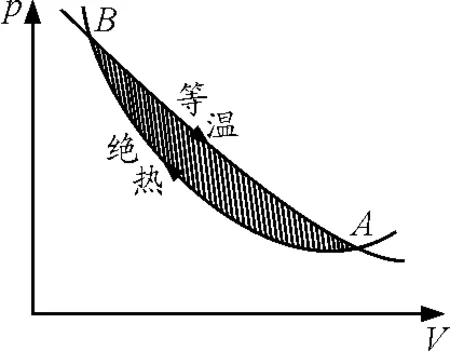
图1 理想气体p-V图

由热力学第一定律得

ΔU=Q-A

B→A在等温过程中有Q>0

A→B在绝热过程中有Q=0

则有

Q=A

式中各字母代表的意思分别是:Q:系统从外界吸热；A：外界对系统做功；U:内能增加.

这与热力学第二定律开尔文氏表述相矛盾(不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响).

因此，假设不成立原结论正确．

上述证明过程完全应用我们物理知识中的热力学第一、二定律进行证明，证明过程虽简单，但不易理解，为此我们介绍下面一种证法．

2 证明方法二

对于“理想气体绝热线与等温线不能相交于两点”这一命题的证明，不依赖于热力学第二定律，也可以证明其正确性．

在pV图中，可设(p1，V1)和(p2，V2)是等温线和绝热线的两个交点，根据理想气体等温过程方程

pV=C1

可得

p1V1=p2V2

(1)

根据理想气体绝热过程方程

pVγ=C2(泊松公式)

可得

(2)

联立(1)、(2)两式可得

其实两个交点为同一点．

在上述的讨论中我们假定γ为常数，而对于理想气体，γ有可能是温度的函数，在此情况下有

nCVdT+pdV=0

(3)

利用理想气体物态方程：pV=nRT,可将式(3)化简为

VF(T)=常量

因此，当γ与温度有关时，理想气体的绝热过程方程为

VF(T)=常量

(4)

设(p1,V1)和(p2，V2)是等温线和绝热线的两个交点,等温线对应的温度为T，由式(4)可得

V1F(T)=V2F(T)

(5)

由等温过程方程可得

p1V1=p2V2

(6)

联立(5)、(6)两式可得

上面两式同样说明，等温线和绝热线的两个交点实为一点，这说明等温线和绝热线不可能有两个或两个以上的交点．

3 两种证明方法比较

相同点：对理想气体绝热线与等温线不能相交于两点这一命题的两种证明方法，本文均采用了反证法，但其应用原理不同．

不同点：

(1)方法一通过应用热力学第一定律导出其与热力学第二定律相矛盾从而证明了其正确性；方法二则采用热力学第一定律的微分形式、理想气体的物态方程及泊松方程进行证明，更多的是数学推理．

(2)方法一形式简单，但不易理解，尤其对其两大定律理解不清晰或不透彻者．方法二虽形式复杂公式繁多实则原理简单，大多是一些数学方面的定性分析及推理，较易理解．

4 总结

对理想气体绝热线与等温线不能相交于两点的正确性的论证，我们从上述问题的两种证明方法进行了证明，均有优缺点，同学们可以自选方法来更好的理解．同时也启示我们，在解决一些问题时要从多角度去思考，力图寻求多种方法来解决其问题，从而得到最简便的解决途径．这不仅可以提高我们解决问题的能力更能锻炼我们的思维能力．

1 刘全慧，沈抗存.热物理教与学随笔集.北京:科学出版社,2010.89～90

2 赵凯华，罗蔚茵. 热学. 北京：高等教育出版社， 2011. 222～223

3 程守洙，江之永.普通物理学.北京：高等教育出版社，2013