人工骨支架结构的单元设计及分析

杨 辉,齐建昌

(东南大学机械工程学院，江苏 南京 211189)

在组织工程学领域，支架起着支撑及引导组织再生的功能，理想的支架要与真实骨的力学性能相匹配。三维周期性极小曲面(TPMS)[1-2]，由于其孔径大小、孔的形状、空隙率可控以及孔与孔之间相互连通等优点，为设计者提供了较大的自由度，故用TPMS设计支架引起学者的广泛关注。

文献[3]用TPMS单元库中的IWP分别于P、G融合，生成结构上更加复杂的支架，并在CATIA CAE模块模拟支架的受力情况，分析支架的应力分布；文献[4]使用薄板样条径向基函数设计非均质化支架，计算G单元在不同空隙率下的杨氏模量。

文献[5]在Rhino中设计12种多面体单元，并在ABAQUS中分析单元在弹性形变范围内的受力情况，比较不同单元的杨氏模量；文献[6]使用模拟和实验的方法分析TPMS单元的塑性变形过程，重点研究了P、D单元在体积分数为30%和60%时的应力应变曲线；文献[7]在ANSYS中分析Kelvin单元的弹性变形过程，主要研究了单元的体积分数与杨氏模量之间的关系，并用实验的方法验证了模拟结果。

文献[8]在ABAQUS中分析G单元的弹性变形过程，主要研究了空隙率为55%和70%两个模型，并在Fluent中模拟了支架内部的流动性；文献[9]主要研究P、IWP单元的空隙率与曲面厚度以及曲面半径之间的关系，并在ABAQUS中分析曲面厚度、曲面半径取不同值时，单元的杨氏模量的变化规律。

本文在分析TPMS单元的基础上，根据距离场设计保持其拓扑连通的人工单元，并在ABAQUS中分析TPMS偏置单元和人工单元的杨氏模量。

1 三维周期性极小曲面

1.1 TPMS的三角函数表示形式

TPMS中的P、D、G、IWP 4种经典类型曲面的三角函数表示形式为[1]：

(1)

式中：X=2πx，Y=2πy，Z=2πz，其中x∈R，y∈R，z∈R。规定φ<0表示隐式曲面的内部，φ>0表示隐式曲面的外部，则式(1)中的φG,φIWP的隐式方程需要反向。

1.2 单元的体积分数与空隙率

TPMS曲面在三维空间中是复杂几何及拓扑连通的结构，其将三维空间分割为内外两部分，并且内外空间的体积相等。将曲面裁剪成实体可以更好地观察其几何拓扑形态，比如曲面P(φP=0)对所在空间进行分割，其内部空间为杆系结构(φP≤0)，外部空间成复杂的孔洞结构(φP≥0)。

定义1：给定TPMS曲面φ，TPMS实体单元定义为{φ(x,y,z)≤0|∀x,y,z∈R,0≤x≤1,0≤y≤1,0≤z≤1}。

图1展示了TPMS实体。设TPMS实体单元内部所围成的体积为V，其最小包围盒体积为VBox，则单元空隙率定义为：

(2)

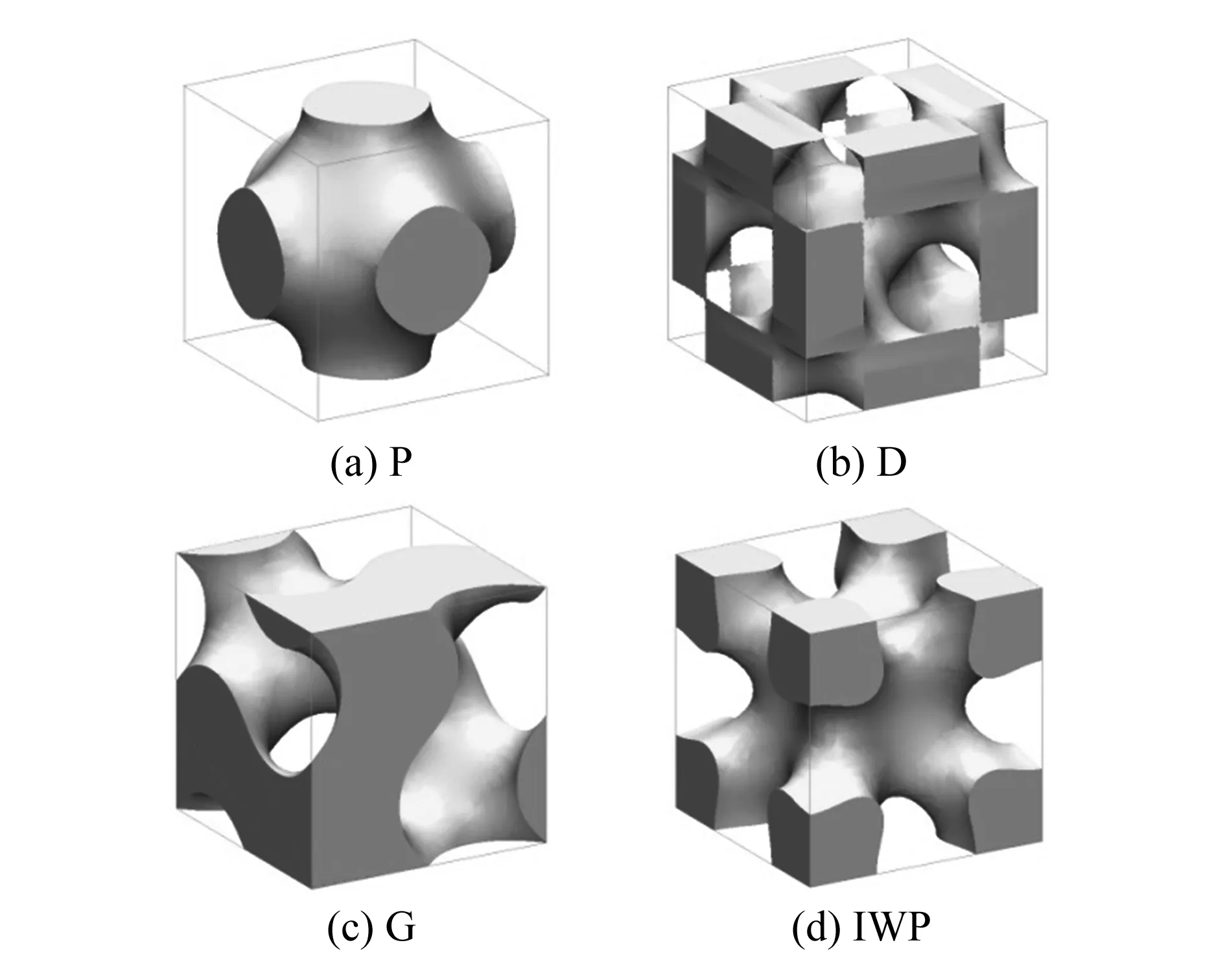
图1 TPMS实体单元

2 保持拓扑连通的人工单元设计

2.1 TPMS单元问题描述

式(1)所描述的TPMS曲面可进行内外偏置(φ=t)，常量t为负数时进行内偏置，常量t为正数时进行外偏置，TPMS曲面偏置后通过对空间的分割得到减薄或加厚的TPMS实体。规定当t≠0为偏置单元，用Po,Do表示。

当TPMS曲面进行内偏置时，随着偏置量的增大，曲面向中心线方向压缩的过程中会出现自相交，对应的实体会被截断，从而无法保证连通性，很难获得高空隙率 (p>90%) 的支架。

如图2(a)～(c)所示，P单元常量t为0时，空隙率为50%，杆系交汇处凸起较明显，在制作时会浪费材料；当常量t为-0.8时，空隙率为73%，杆系半径明显减小；当常量t为-1.0时，杆系出现自相交现象，无法保证连通性。图2(d)～(f)展示了D单元随着空隙率的增大，出现了杆系断裂的现象。

2.2 TPMS单元的拓扑分析

TPMS原始单元(t=0)很难观察其拓扑连通性，为了方便观察，将原始单元进行内偏置得到减薄单元。如图3所示，各个杆系用圆柱表示，记录圆柱中心线两端点坐标；杆系汇交处用小球表示，并记录球心的坐标。球心坐标、圆柱中心线端点坐标以及坐标间的连通关系用于设计人工单元。

图2 空隙率逐渐增大出现的杆系自相交和断裂

图3 TPMS单元的拓扑连通图

由图3中的球和圆柱的连通规律可知，P单元为六连通结构，D单元为四连通结构，G单元为三连通结构，IWP单元为八连通结构。

2.3 人工单元设计

TPMS的拓扑常见于真实骨的结构中，市场迫切需要一种既保持TPMS单元的拓扑连通性，又能得到高空隙率的支架。2.2节具体分析了单元的拓扑连通性，并记录了关键数据点的坐标，借助这些信息就能够得到TPMS杆系结构的中心线分布，再以中心线为轴，求出光滑过渡的等距面，就能得到满足设计需求的人工单元。

由距离场设计人工单元的步骤如下：

1)在空间中等距离布点，并记录点的坐标。

2)由TPMS的拓扑连通图得到其中心线分布。

3)计算点到各中心线的距离，记为di。

4)由距离函数F(d)求得各点处的总场强。

(3)

5)MarchingCubes算法显示曲面。

图4给出了由TPMS单元设计人工单元的主要过程，用Pt表示人工单元。

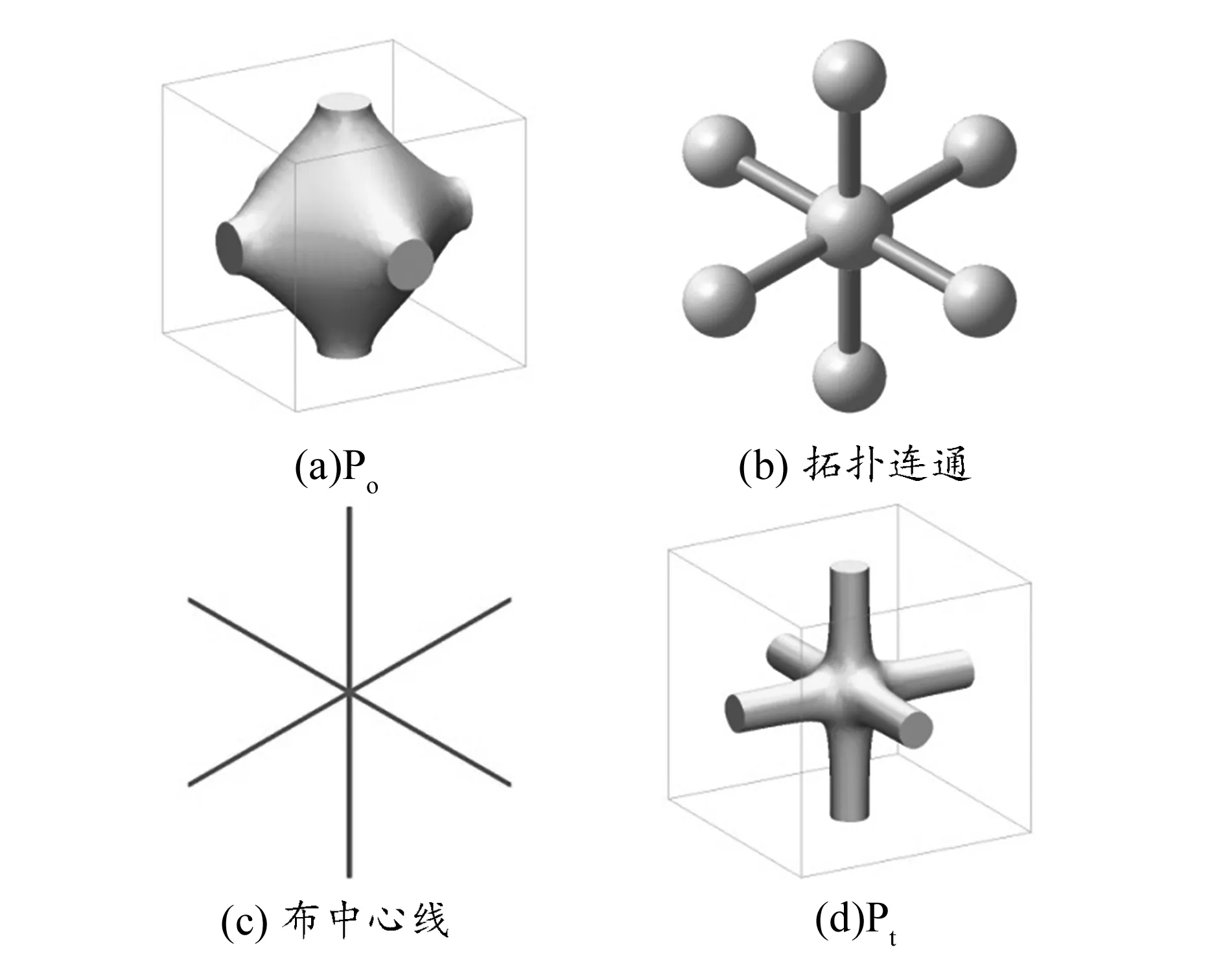
图4 由TPMS单元设计人工单元的主要过程

3 单元分析

将由P单元组成的四面体网格模型导入到ABAQUS CAE中，图5展示了有限元分析过程，首先给模型赋予材料属性[10]，弹性模量E=2GPa，泊松比为0.3；然后设置边界条件，限制底面的6个自由度，顶面位移为压缩方向的1%，提交分析直至达到平衡状态，求得此时网格顶部节点处的反作用力F。设网格模型的最小包围盒横截面面积为A，压缩方向的初始长度为L，压缩量为ΔL，应变用ε表示，则有效杨氏模量Ef定义为：

(4)

其中应变ε定义为：

(5)

图5 有限元分析的主要过程

3.1 Ef与单元阵列的关系

选择单元尺寸为1mm、空隙率为75%的P单元进行分析，将P的偏置单元(Po)和人工单元(Pt)分别装配为1，2×2×2，3×3×3，4×4×4，5×5×5的结构。将上述四面体网格模型导入ABAQUS CAE中，底面固定，顶面压缩，压缩量为Y方向长度的1%，记录平衡状态下顶部节点处的反作用力F，根据式(4)求得该结构的有效杨氏模量Ef。图6展示了空隙率为75%时，P单元的有效杨氏模量(单位为MPa)与单元阵列的关系。

图6 Ef与单元阵列的关系

由图6可知，当空隙率为75%时，P的人工单元的有效杨氏模量大于偏置单元。可能的原因是，在该空隙率下，偏置单元在杆系汇交处凸起较明显，单元拼接处的杆系半径过小，使结构出现薄弱环节，经优化后的人工单元，材料绕杆系中心线分布更加均匀，故抵抗弹性变形能力更强；随着单元阵列数目的变化，P的偏置单元和人工单元的有效杨氏模量出现微小的波动，若考虑造型过程中空隙率的微小偏差以及网格质量差异对分析结果造成的影响，可近似认为，单元的有效杨氏模量为一定值。根据上述分析，可得出如下结论：1)当空隙率为75%时，P的人工单元抵抗弹性变形能力优于偏置单元；2)当空隙率为75%时，P的偏置单元和人工单元的有效杨氏模量均与单元阵列数目无关。

3.2 Ef与空隙率的关系

通过曲面偏置可得到不同空隙率单元，取单元阵列为2×2×2，单元尺寸为1mm，空隙率为30%～75%(步长为5%)共10个模型进行分析，将模型导入ABAQUS CAE中，底面固定，顶面压缩，压缩量为0.02，记录平衡状态下顶面节点处的反作用力F，根据式(4)求得结构的有效杨氏模量Ef。图7展示了单元阵列为2×2×2时，P单元的有效杨氏模量(单位为MPa)与空隙率的关系。

由图7可知，随着空隙率的增大，P的偏置单元(Po)和人工单元(Pt)的有效杨氏模量减小，且偏置单元的下降速度更快。当空隙率小于55%时，P的偏置单元的有效杨氏模量大于人工单元；当空隙率大于55%时，P的偏置单元的有效杨氏模量小于人工单元，出现此现象的原因在于，随着空隙率的增大，P的偏置单元杆系半径减小速度快于人工单元，而单元拼接处是该结构最薄弱的位置。根据以上数据，可得出如下结论：1)随着空隙率的增大，P的偏置单元和人工单元的有效杨氏模量均减小；2)随着空隙率的增大，P的偏置单元的有效杨氏模量减小的速度大于人工单元。

图7 Ef与空隙率的关系

4 结束语

TPMS单元作为支架设计的造型单元有其独特的优势，比如空隙率可控，拓扑连通规律与骨小梁类似等，但是很难得到高空隙率的支架。而本文提出的应用距离场设计保持TPMS拓扑连通的人工单元的方法，能够得到更高空隙率的支架。由于条件限制，文中仅做了理论分析和有限元模拟，缺乏试验数据做支撑，因而后续工作将尽可能与相关企业及其他高校合作，将试验数据补充完整。

[1] SCHOEN A H. Infinite periodic minimal surfaces without self- intersection[M]. Cambridge: National Aeronautics and Space Administration,1970.

[2] JUNG Y, CHU K T, TORQUATO S. A variational level set approach for surface area minimization of triply-periodic surfaces[J]. Journal of Computational Physics,2007,223(2):711-730.

[3] YOO D J, KIM K H. An advanced multi-morphology porous scaffold design method using volumetric distance field and beta growth function[J]．International Journal of Precision Engineering and Manufacturing,2015,16(9):2021-2032.

[4] YOO D. Heterogeneous minimal surface porous scaffold design using the distance field and radial basis functions[J]．Medical Engineering & Physics,2012,34(5):625-639.

[5] WETTERGREEN M A,BUCKLEN B S,STARLY B,et al. Creation of a unit block library of architectures for use in assembled scaffold engineering[J]．Computer-Aided Design,2005,37(11): 1141-1149.

[6] KADKHODAPOUR J, MONTAZERIAN H, RAEISI S. Investigating internal architecture effect in plastic deformation and failure for TPMS-based scaffolds using simulation methods and experimental procedure[J]．Materials Science & Engineering C,2014,43(43):587-597.

[7] ZARGARIAN A, ESFAHANIAN M, KADKHODAPOUR J, et al. Effect of solid distribution on elastic properties of open-cell cellular solids using numerical and experimental methods[J]．Journal of the Mechanical Behavior of Biomedical Materials,2014,37(37C):264-273.

[8] OLIVARES A L, ELIA M, PLANELL J A, et al. Finite element study of scaffold architecture design and culture conditions for tissue engineering[J]．Biomaterials,2009,30(30):6142-6149.

[9] ALMEIDA H A, BARTOLO P J. Design of tissue engineering scaffolds based on hyperbolic surfaces:structural numerical evaluation[J]．Medical Engineering & Physics,2014,36(8):1033-1040.

[10] SUN W, DARLING A, STARLY B, et al. Computer-aided tissue engineering: overview, scope and challenges[J]．Biotechnology & Applied Biochemistry,2004,39(1):29-47.