含分布式电源的区间多目标微网规划

李二超，张建军

(兰州理工大学电气与信息工程学院，甘肃 兰州 730050)

由于化石能源造成的环境污染日益严重，因此可再生能源以可持续使用和环保的特点被广泛关注。分布式发电是以可再生能源为一次能源，其主要优点有能源种类多、损耗低、投资少、效率高、系统可靠性高、选址容易[1]，因此有必要在传统的配电网中引入分布式电源(DG)。含分布式电源的配电网规划是一个多目标优化问题，目前已有一些专家对含分布式电源配电网规划进行了研究[2-4]。

文献[2]以保证分布式电源的运行总费用、配电网线路升级及电网维护费用和电网网络损耗费用为目标，通过设置加权系数，将含分布式电源的配电网规划的多目标优化问题转化为单目标优化问题，最后采用遗传算法优化出规划方案。在该方法中，因为目标函数权重的设置在很大程度上受到主观因素的影响，很难客观地权衡各目标的重要程度，不能保证获得最优的方案。文献[2]中，在负荷节点接入的分布式电源没有进行容量约束限制，如果在某个负荷节点接入的分布式电源容量大于负荷就会改变配电网的潮流方向，使配电网原有的继电保护失效。文献[3]以保证配电网年费用最小为前提，研究了含分布式电源的配电网规划问题，采用遗传算法对分布式电源的容量和位置进行优化，再运用基于支路交换的模拟退火算法进行网络扩展规划。上述文献都没有考虑加入分布式电源的配电网向发电厂的购电费用和在负荷节点接入的分布式电源容量约束问题。由于风力和光伏发电系统等的出力受天气变化的影响，其功率输出具有不确定性和随机性，同时在实际的配电网中，负荷并不是恒定不变的，要考虑负荷的不确定因素。文献[5]考虑了负荷的不确定性，采用区间分析的方法对潮流计算方程组进行求解，但是该文献没有考虑分布式电源出力不确定因素。文献[6]考虑了分布式电源出力不确定的因素，采用复仿射潮流算法来分析分布式电源对配电网的影响，但是该文献只考虑了分布式电源出力不确定因素，没有考虑负荷的不确定性。对于不确定优化问题，根据不确定参数描述的不同，一般有随机规划和模糊规划两种解决方案[7]，这两种方案分别依赖于模糊隶属度函数和参数的随机概率分布，但是在实际工程中很难获得这些信息。相反，可以很容易获得这些参数的取值范围，因此用区间数表示不确定参数更具有实际意义[8]。

在含分布式电源的多目标配电网规划的数学模型中有大量的约束条件，常规的约束处理方法有罚函数法[9]，然而这种方法解决约束优化问题的关键是构建一个好的惩罚函数。在优化算法中，惩罚项太小或者太大都会影响优化的结果，目前很难客观地构建出一个好的惩罚函数。文献[10]提出了一种多目标优化约束方法，将约束违反度作为目标函数，利用可行性规则来处理约束，但是对于可行解来说，约束违反度为零，其实质还是单目标优化。

本文在含分布式电源的配电网规划中，考虑负荷不确定性和分布式电源出力的不确定性，采用区间迭代方法求解潮流方程组，分别得到节点电压幅值和相角的上下限。在分布式电源的运行总费用、电网网络损耗费用的基础上增加含分布式电源的配电网向发电厂的购电费用。在配电网规划的约束中加入负荷节点接入分布式电源容量的约束，提出一种基于改进的可行性规则的约束处理方法，将该约束处理方法引入到IP-MOEA[11]中。这种改进的可行性规则充分结合了违反度信息和非支配层数信息，利用违反度信息和非支配层数信息在迭代的过程中从各个方向向可行解逼近，使得收敛速度更快，找到的可行解更多。最后以IEEE33节点系统为例进行仿真，仿真结果表明本文所提方法具有较高的决策效率，在保证配电网经济性的同时，也使整个配电网的网络损耗得到了明显的降低。

1 区间数与区间算法

区间方法作为求解区间问题的一种方法，用区间来描述参数的不确定性，现已建立了一套完整的区间运算规则[12-14]。

1.1 区间与区间数

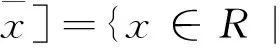
(1)

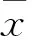
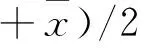
(2)

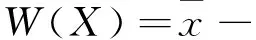
(3)

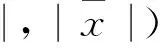
(4)

1.2 区间数的基本运算规则

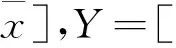
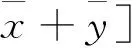
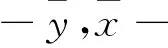
(5)

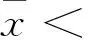
2 微网规划的数学模型

本文假定配电网规划期限为20 年，且配电网各个节点已经存在，负荷需求以每年1% 的速度递增。

本文采用了含分布式电源的配电网规划经济性模型[15]，该模型主要以线路损耗费用、每年的分布式电源的投资及运行费用、加入分布式电源后购电费用为目标函数。在分布式电源位置、个数和单个电源容量均不确定的情况下对位置和容量变量采用实数编码的方法。假设一个负荷节点只能安装一个分布式电源。为了保证配电网的电能质量，本文在含分布式电源的配电网规划经济性模型中引入了节点电压区间约束、每条支路传输容量区间约束、导线电流区间约束、节点的功率平衡约束、分布式电源在电网的总接入容量区间约束以及安装的分布式电源装机容量区间约束。

2.1 含分布式电源的电网规划多目标模型

1)分布式电源运行总费用CDG。

分布式电源的总费用包括安装费用、燃料费用和运行维护费用，本文将这些费用转化为发电总成本，作为目标函数。假设将接入配电网的分布式电源所采用的模型当作具有恒定功率因数η的PQ节点，同时假设各节点负荷的用电性质相同，分布式电源的最大发电小时数Tmax相同。

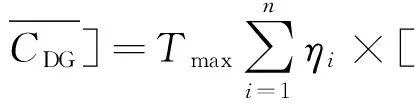
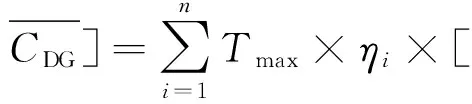
(6)

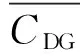
2)线路损耗费用CL。

(7)

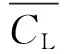
3)引入分布式电源后购电费用Cen。

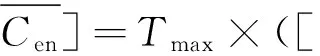
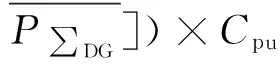
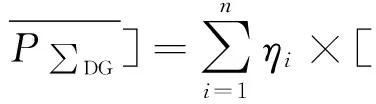
(8)

2.2 含分布式电源的电网规划区间约束的模型

分布式电源接入配电网后会改变配电网原有的潮流，为了使这种改变在可控的范围内，需要对分布式电源的容量进行限制。另外，因为分布式电源的启、停机不受电力系统调度部门的控制，所以如果单台机组容量过大，启、停机时就会对周围用户的用电造成较大影响。因此本文加入了对分布式电源总出力的约束，即假设分布式电源接入电网的总容量不超过电网最大负荷总量的15%[16]。

1)节点电压区间约束。

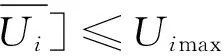
(9)

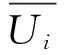
2)支路电流区间约束。

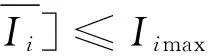
(10)

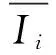
3)每条支路传输容量区间约束。

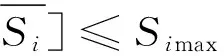
(11)

4)负荷节点的分布式电源装机容量区间约束。

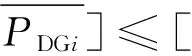
(12)

5)分布式电源在电网的总接入容量区间约束。

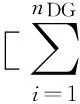
(13)

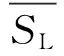
本文同时考虑了分布式电源出力的不确定性和负荷的不确定性，建立了含分布式电源的电网规划多目标区间模型，在求解该模型过程中，传统的潮流计算已不再适用区间问题，需要使用区间潮流计算方法，然而该模型中约束条件比较多，导致满足众多约束的可行解不易被找到，因此需要一种更加有效的约束处理方法。

3 基于改进可行性规则的约束处理结合IP-MOEA 算法

3.1 IP-MOEA 算法的特点

非精确传播多目标进化算法——IP-MOEA[11]就是在NSGA2[17]框架下，通过将Pareto占优关系和拥挤距离推广至区间范围。IP-MOEA算法将NSGA2算法中的拥挤距离和非支配排序替换为超体积和基于区间的占优关系。

3.2 可行性规则的特点

可行性规则[18]是由DEB 提出的约束处理的规则，这个规则是利用对可行解的偏好来选择个体。

1)如果在两个不可行解之间进行比较，选择约束违反度较低的个体进入下一代。

2)如果在可行解和不可行解之间进行比较，选择可行解进入下一代。

3)如果在两个可行解之间进行比较，选择函数值更好的个体进入下一代。

由此可知，这种可行性规则适用于单目标的情况。在文献[10]中，使用了一种多目标约束处理方法，将“最好”的不可行解放到一个预先设定好的集合A中。“最好”的不可行解就是有最小的违反度值，以便在后边的进化过程中替换掉有最大的违反度值的解。

3.3 基于可行性规则改进的多目标约束处理方法

1)当可行解和不可行解进行比较时，可行解进入下一代，如果不可行解是非支配个体，或者不可行解所在的非支配层数比可行解所在的非支配层数小，则将不可行解放到预先设定好的集合A中。在以后的进化过程中，使用替换规则让A中的个体参与到进化过程中。

2)当两个可行解进行比较时，让所在非支配层数低的个体进入下一代，另一个个体放到预先设定好的集合A中。在以后的进化过程中，使用替换规则让A中的个体参与到进化过程中。

3)当两个不可行解进行比较时，让违反度低的进入下一代，如果另一个违反度高的个体是非支配个体则放到预先设定好的集合A中。在以后的进化过程中，使用替换规则让A中的个体参与到进化过程中。

由此可知，这种改进的可行性规则充分结合了违反度信息和非支配层数的信息，最终所求的最优解是违反度为零且非支配层数最小的解，所以利用违反度信息和非支配层数信息在迭代的过程中从各个方向向可行解逼近，使得收敛速度更快，找到的可行解更多。

3.4 基于改进的可行性规则的IP-MOEA 区间多目标优化流程

本文所提出的基于改进的可行性规则的IP-MOEA多目标优化算法流程如下：

1)编码。

分布式电源的建设方案运用一组变量C={c1,c2,…,cn}来表示。若ci=0,则表示负荷节点i没有安装分布式电源；若ci=1，则表示负荷节点i上待建分布式电源，且安装容量为1MVA；若ci=2，则表示该负荷节点i上待建分布式电源的安装容量为2MVA。依此类推。

2)初始群体的产生。

随机初始化50个个体，每个个体用C={c1,c2,…,cn}表示，ci一般取为整数，因此C={c1,c2,…,cn}是一组离散值。

3)区间潮流计算[19]。

初始化种群产生后，由于每个负荷节点上都有可能增加分布式电源，将加入分布式电源的配电网进行区间潮流计算，通过区间潮流计算得到配电网网络损耗上下限、节点电压上下限等。

4)非支配排序。

将每个个体按照目标函数值区间进行基于区间占优关系的非支配排序，同时计算每个个体的超体积。

5)锦标赛选择。

在进行非支配排序后的种群中通过锦标赛选择来选取父代种群。

6)遗传操作[20]。

遗传操作包括交叉操作和变异操作。

7)改进的可行性规则选择。

通过遗传操作产生新的子代，将子代和原始种群运用改进的可行性规则进行选择，让优秀的个体进入下一代。如果另一个个体满足改进的可行性规则条件，则将其放到预先设定好的集合A中，以便在以后的进化过程中使用替换规则替换掉不好的个体。通过这种选择策略不仅可以得到可行解，而且所得到的可行解中大部分是非支配个体。

8)个体替换。

经过改进的可行性规则选择之后，集合A中存放了一些可被利用的个体。如果种群中个体的违反度和非支配层数都比集合A中的个体大，则集合A中的该个体将替换掉种群中相应的个体。

9)变异操作。

经过以上操作，如果种群中的个体全部是不可行解或者全部是被支配解，则对种群进行变异操作，即在种群中随机选取一个个体，对其染色体的某个基因进行变异操作。

4 算例分析

为了验证本文所提算法和模型的有效性，以图1 所示的IEEE33 节点配电网系统为例进行计算分析。线路参数见文献[21] ，假设每个节点负荷的变化在10%以内。

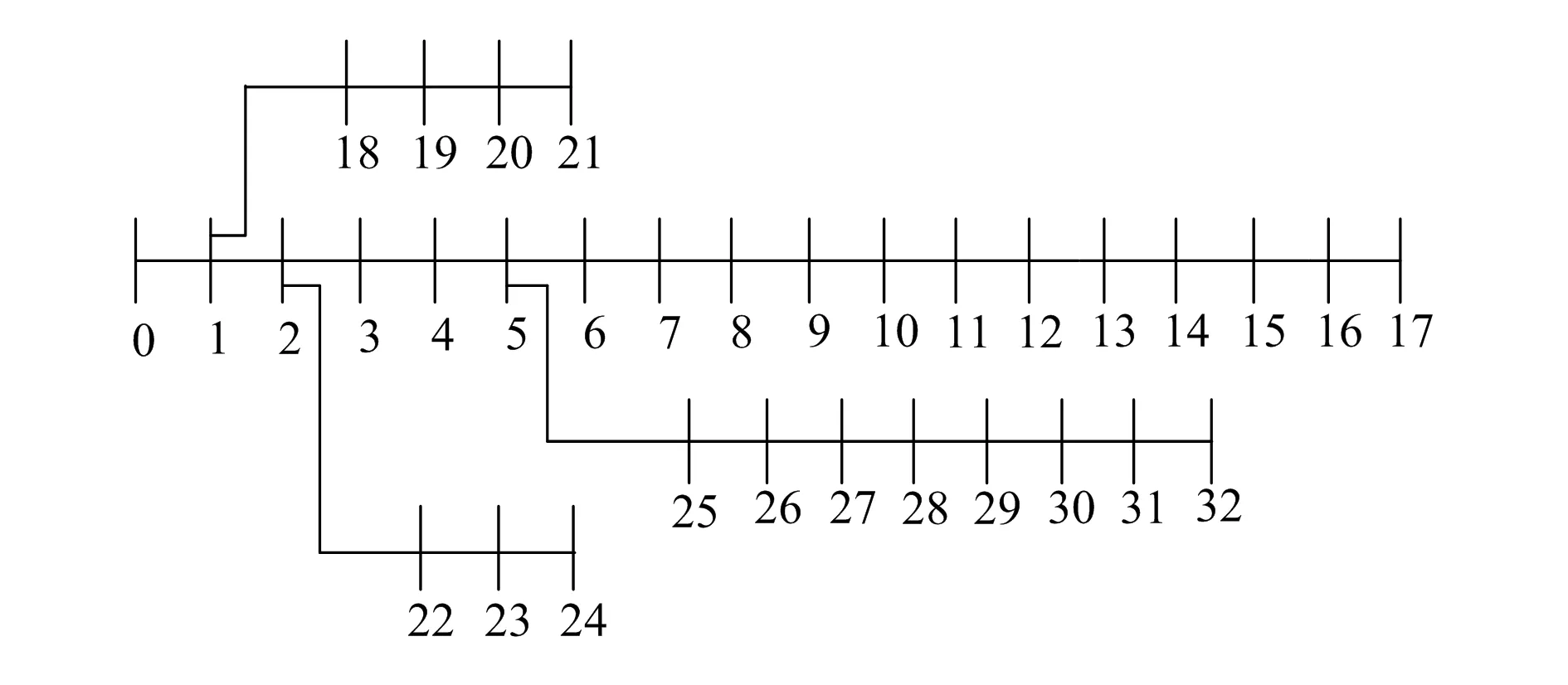
图1 IEEE33节点

图2是只考虑负荷不确定的模型经过本文所提算法优化得到的Pareto最优解集。对于单目标区间优化模型，所求的解是一维坐标系上的一段区间；对于两目标区间优化模型，所求的解是二维坐标系中的一个平面；对于三目标区间优化模型，所求的解是三维坐标系中的一个立方体。从图2可知，只考虑负荷不确定性所得的Pareto最优解集是三维坐标系的平面，因为本文中的目标函数1是分布式电源总的运行总费用，与负荷无关，当负荷发生变化时，目标函数1恒定不变，且目标函数1的上下限相等，但是目标函数2和目标函数3会随着负荷的变化而改变，从而在三维空间中形成一个平面，所以只考虑负荷不确定模型所求的解是三维空间中的平面。

图2 只考虑负荷不确定优化产生的结果

图3是只考虑分布式电源出力不确定的模型经过本文所提算法优化得到的Pareto最优解集。因为本文中的3个目标函数都会随着分布式电源出力的变化而发生改变，从而在以这3个目标值为坐标系的三维空间中形成一个立方体，图中的每个立方体区域都代表一个解的区间范围，因此区间内的个体是满足所有的约束条件，决策者也应该从这些立方体中选择合适的解。

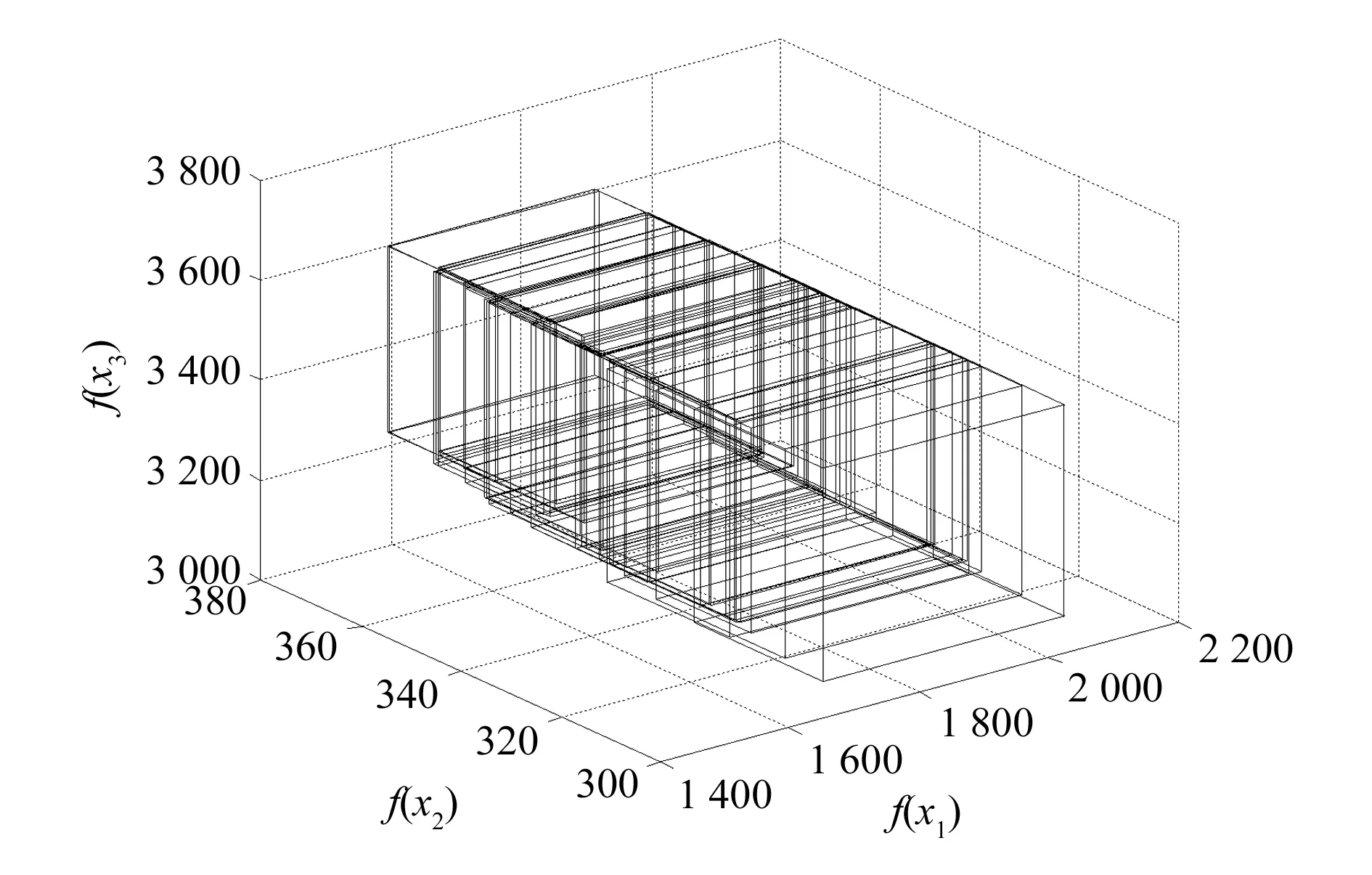
图3 只考虑分布式电源出力不确定优化产生的结果

图4是同时考虑负荷不确定和分布式电源出力不确定的模型经过本文所提算法优化得到的Pareto最优解集。本文所使用的3个目标函数都会随着负荷和分布式电源出力的变化而发生改变，从而在以这3个目标值为坐标系的三维空间中形成一个立方体，图中的每个立方体区域都代表一个解的取值范围。图中的*代表每个区间解的中心，决策者从这些*中选择一个违反度为0、非支配层数为1的个体，超体积最大的中心点，可以得到分布式电源接入配电网的最佳位置和容量。

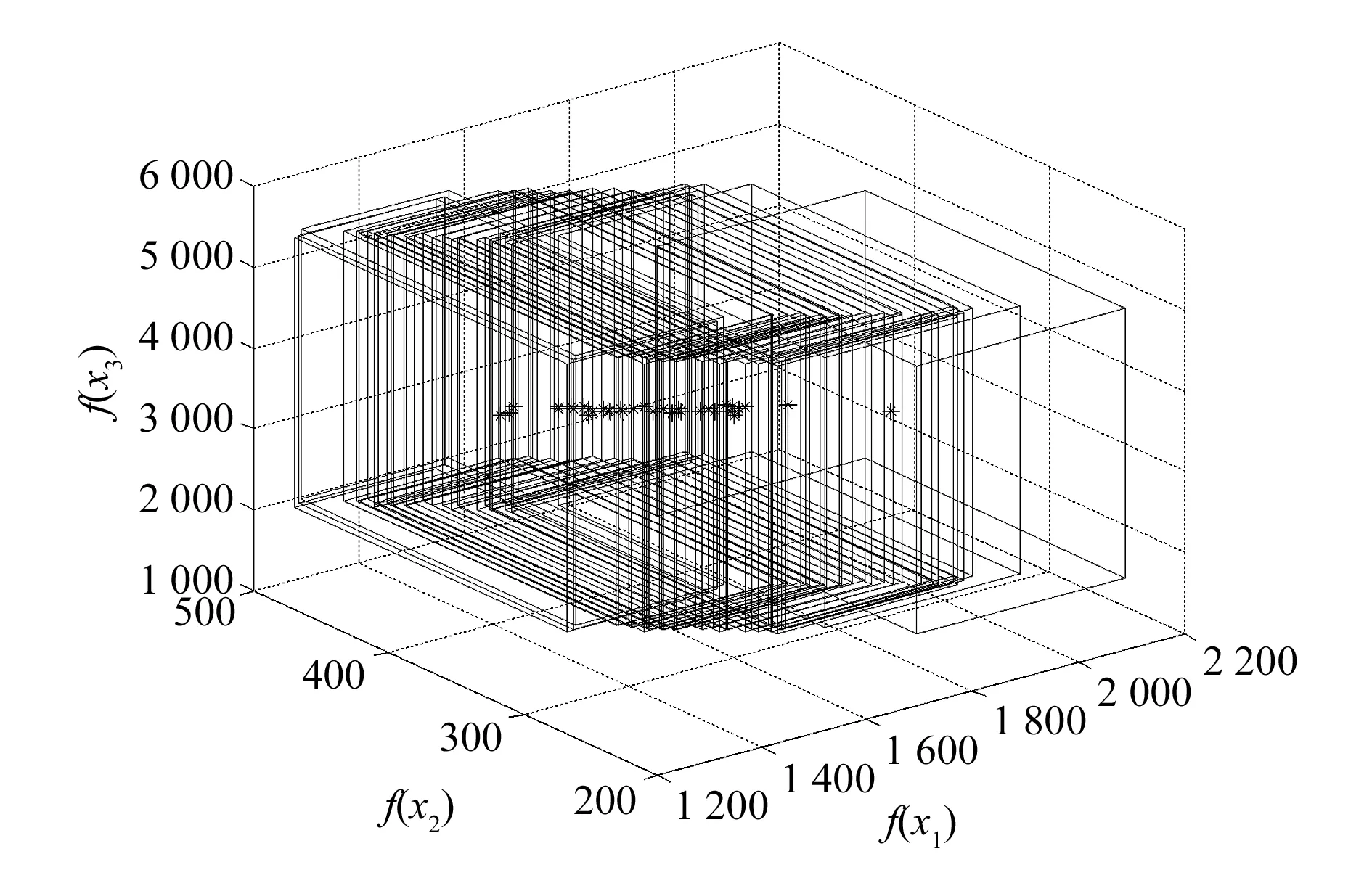
图4 考虑负荷不确定和分布式电源

图2～4所示的结果分别是在相同的参数下，各自独立运行30次、迭代次数为100代得到的实验结果。通过对比以上3组实验结果，可以明显地发现同时考虑负荷不确定和分布式电源出力不确定模型所得个体解的区间，包含了只考虑分布式电源出力不确定模型所得解的区间和只考虑负荷不确定模型所得解的区间。因此同时考虑负荷不确定和分布式电源出力不确定模型更具有实际意义，能够为决策者提供更好的、更符合实际的最优解。

从表1可以看出，由于分布式电源对线路负载能力和配电网潮流的影响，分布式电源主要位于辐射状配电网线路的末端。

表1 分布式电源的接入位置和容量

由表2分析可知，虽然不含分布式电源的方案中分布式电源运行费用为0，但是增加分布式电源后的线路损耗费用区间值和配电网向发电厂的购电费用区间值明显减小，同时还能明显降低网损，因此加入分布式电源后的配电网的经济效益得到了改善。

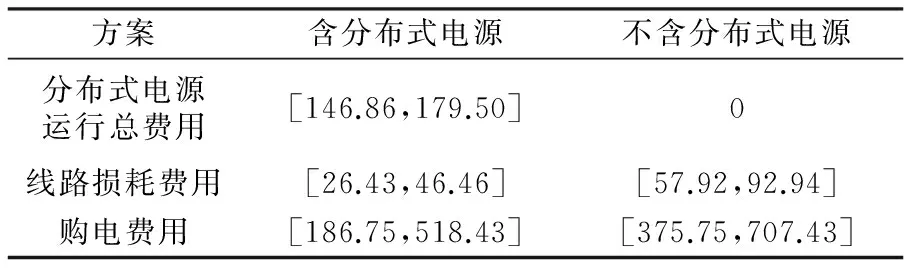
表2 不同规划方案的费用比较 万元

由表3可知，加入分布式电源后的配电网线路损耗得到了明显的改善，在降低线路损耗及保护环境的同时也节约了资源，符合国家环境保护的政策。

表3 不同规划方案的功率损耗比较 kW

5 结束语

在实际的微网系统中，分布式电源功率输出具有随机性，同时配电网中也存在负荷等量的不确定因素，共同导致了配电网潮流的不确定性。目前的研究文献没有同时考虑配电网中分布式电源出力随机性和负荷不确定性，本文同时考虑两种不确定性建立了以折算到每年的线路损耗费用、分布式电源的投资运行费用、购电费用最小为目标的多目标优化区间模型，引入区间数学求解本文所提模型。同时提出将违反度信息和非支配层数信息引入到可行性规则约束处理方法中，并且将该处理约束方法引入到IP-MOEA算法中。以IEEE33节点配电网系统为例进行了仿真分析，结果表明该方法具有较高的决策效率，在保证配电网经济性的同时，也使整个配电网的网络损耗得到了明显的降低。本文对在配电网中加入分布式电源的规划具有一定的指导作用。

[1] EL-KHATTAM W, SALAMA M M A. Distribution system planning using distributed generation[C]// IEEE Canadian Conference on Electrical and Computer Engineering, 2003.Piscataway: IEEE, 2003:579-582.

[2] 张琦.电网规划中分布式电源的选址和定容[D].济南:山东大学,2008.

[3] 王成山,陈恺,谢莹华,等.配电网扩展规划中分布式电源的选址和定容[J].电力系统自动化,2006,30(3):38-43.

[4] 刘杨华,吴政球,涂有庆,等.分布式发电及其并网技术综述[J].电网技术,2008,32(15):71-76.

[5] 裴爱华,刘明波,张弛.考虑负荷不确定性的区间潮流计算方法[J].电力系统及其自动化学报,2004,16(6):24-28.

[6] 王守相,韩亮.DG 出力不确定性对配电网影响力分析的复仿射数学方法[J]. 中国电机工程学报,2014,34(31):5507-5515.

[7] 程志强, 戴连奎, 孙优贤. 区间参数不确定系统优化的可行性分析[J]. 自动化学报,2004,30(3):455-459.

[8] 章恩泽, 陈庆伟. 不确定可靠性优化问题的多目标粒子群优化算法[J]. 控制与决策,2015,30(9):1071-1075.

[9] HOMAIFAR A, QI C X,LAI S H.Constrained optimization via genetic algorithms[J]. Simulation Transactions of the Society for Modeling & Simulation International,1994,62(4):242-253.

[10] CAI Zixing，WANG Yong. A multiobjective optimization-based evolutionary algorithm for constrained optimization[J]. IEEE Transactions on Evolutionary Computation,2006,10(6):658-675.

[11] LIMBOURG P, APONTE D E S.An optimization algorithm for imprecise multi-objective problem function[C]//Proceedings of IEEE Congress on Evolutionary Computation.New York:IEEE Press,2005:459-466.

[12] MOORE R E. Interval Analysis[M].Englewood Cliffs,NewJersey:Prentice-Hall,1966.

[13] 王守相, 王成山, 刘若沁. 基于模糊区间算法的配电网潮流计算[J]. 电力系统自动化,2000,24(20):19-22.

[14] DAS Biswarup.Radial distribution system power flow using interval arithmetic[J]. International Journal of Electrical Power& Energy Systems, 2002, 24: 827-836.

[15] KAUHANIEMI K, KUMPULAINEN L. Impact of distributed generation on the protection of distribution networks[C]// Eighth Iee International Conference on Developments in Power System Protection.London:IET, 2004:315-318.

[16] CELLI G, PILO F.Optimal distributed generation allocation in MV distribution networks[C]// IEEE Power Engineering Society International Conference on Power Industry Computer Applications, 2001. Piscataway:IEEE, 2001:81-86.

[17] DEB K. A fast elitist multi-objective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2000, 6(2):182-197.

[18] DEB K. An efficient constraint handling method for genetic algorithms[J]. Computer Methods in Applied Mechanics & Engineering，2000,186(2/4):311-338.

[19] 丁涛,崔翰韬,顾伟,等.基于区间和仿射运算的不确定潮流算法[J]. 电力系统自动化,2012,36(13):51-55.

[20] 张琛,詹志辉.遗传算法选择策略比较[J]. 计算机工程与设计,2009,30(23):5471-5478.

[21] NARIMANI M R,VAHED A A, AZIZIPANAH-ABARGHOOEE R.Enhanced gravitational search algorithm for multi-objective distribution feeder reconfiguration considering reliability,loss and operational cost[J].Generation, Transmission & Distribution,2014,8(1):55-69.