基于热源法的涡旋盘高速精密铣削切削热研究
刘 涛,韩晓静
(兰州理工大学机电工程学院,甘肃 兰州 730050)
涡旋压缩机是一种新型容积式流体机械,其核心部件是具有微米级尺寸精度和形位精度的动、静涡旋盘,涡旋盘的精度直接影响压缩机的性能,目前一般采用数控技术对其进行加工。涡旋盘的加工精度受到切削温度、冷却方式、刀具精度等因素的影响。高速切削时,刀具和涡旋盘之间的相互作用导致涡旋盘局部产生剧烈的塑性变形,刀具与涡旋盘间的摩擦产生大量的切削热,导致刀具磨损过快,换刀频繁,使得涡旋盘的加工精度达不到技术要求。针对工件和刀具铣削过程中的切削热问题,LOEWEN和SHAW提出了用热源解析法来研究切削热[1-2]:第一、二变形区切削变形功全部转化为热量,变形区的热源可以看作为平面热源,而且没有热量传递到外界环境中,各个变形区热量均匀分布。关立文等[3]结合热源法、热量分配模型和温度实验结果,提出并建立了“S”形试件完整的间歇性切削温度场模型。刘胜[4]研究了切削加工钛合金工件时工件、刀具和切屑的温度分布及切削力,给出了求解切削温度场和切削力的有限元模型。文献[5]研究了高速断续切削过程中刀具及工件切削温度随切削速度的变化规律,认为合理地控制切削速度可以降低切削温度以及抑制断续切削过程中的热冲击。文献[6]利用传热反求法建立了45钢断续切削过程的分析和实验模型,预测了传入刀具和工件的热源热量分布规律。文献[7]以Al2O3陶瓷材料激光铣削为例,建立了激光多道铣削的三维温度场有限元模型,并利用ANSYS软件进行仿真分析。本文针对变截面涡旋盘加工中的热变形问题,基于热源法建立点和线热源模型,分析了其任意时刻和位置的温升变化规律。利用Cr15Mo材料的J-C (Johnson-Cook)本构模型和剪切面温度场模型,推导出了剪切温度和剪切应力的数学模型,探讨了不同应变下应力-温度的关系和不同温度下应力-应变的关系,对于合理选择铣削参数、控制热变形有一定的理论指导意义。
1 涡旋盘铣削过程中温度的产生及来源
涡旋盘加工过程中形成了3个变形区域,如图1所示。第Ⅰ变形区:在剪切作用下刀具与工件发生相对滑移形成切屑,是切削热产生的主要区域,也被称为剪切区,在该区剪切热全部会转化为热源的热量。第Ⅱ变形区:刀具与切屑摩擦区域,切屑与加工中的涡旋盘分离后,会沿着刀具的前刀面流出,产生了刀屑摩擦。第Ⅲ变形区:刀具、工件的摩擦区,刀具的后刀面与加工的工件表面接触并发生摩擦运动,从而产生了轻微的摩擦形变,且有大量的热生成。

图1 变形区
在涡旋盘加工的过程中,刀具与涡旋盘的摩擦和剪切作用消耗机械能并产生热量积累在切削区,使得刀具和涡旋盘的温度升高,而铣削温度的变化将会降低涡旋盘的加工精度和缩短刀具的使用寿命。
2 涡旋盘的温度场理论分析
2.1 无限大导体内瞬时点热源的温度场
本文采用热源法分析涡旋盘加工中的温度场,热源法是一种利用固体导热微分方程的热源解,经迭加后计算出各种形式温度场的方法,是基于瞬时点热源在无限大介质中瞬时发出一定热量后的任一时刻的温度场的解。
如图2所示,设瞬时点热源位于坐标原点,任一点M(x,y,z)位于距点热源R处。
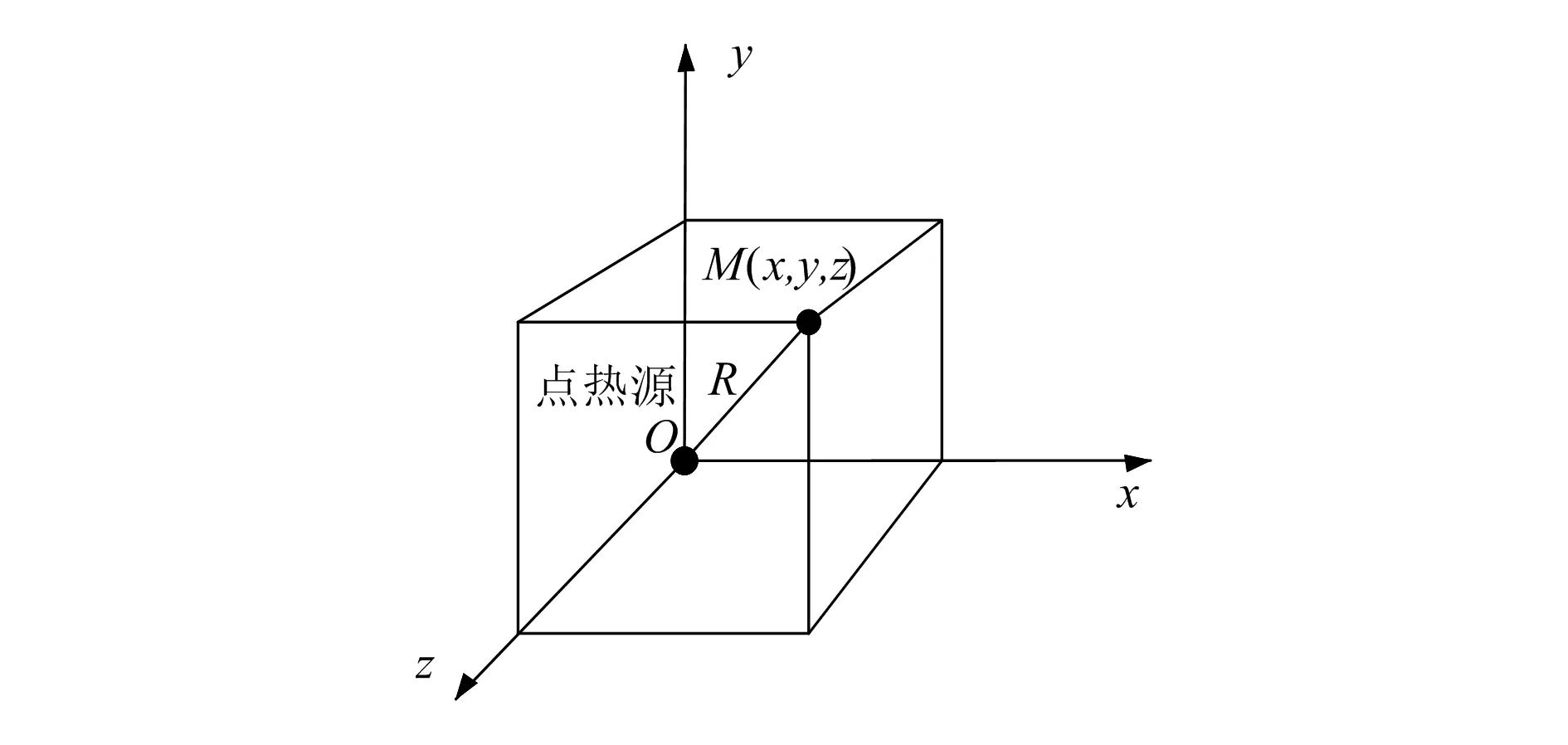
图2 点热源的温度场坐标
首先,建立三维坐标系下的固体热传导数学模型:
(1)

文献[8]推导出具有瞬时点热源的无限大导体的温度解析式:
(2)
式中:Q为瞬时点热源发热量。
若点热源不在坐标原点,而在N(x1,y1,z1)处时,瞬时点热源所在的无限大导体内的温升公式为[8]:
(3)
在实际的铣削加工中,不管热源的形状、尺寸大小如何,是瞬时发热还是持续发热,都可用式(3)作为基础,按照热源温度场的迭加原理,用积分方法推导出不同情况下的温度场计算式。
2.2 涡旋盘瞬时无限大线热源的温度场
在涡旋盘加工的过程中,刀具与工件接触部位可以看作线热源沿切削圆弧运动,如图3所示,线热源可以看作无数微小单元线段热源的组合,而微小线段可近似认为是一个点热源,利用积分法,将无数个点热源所造成的温升进行迭加,最后按照线热源的公式进行求解。
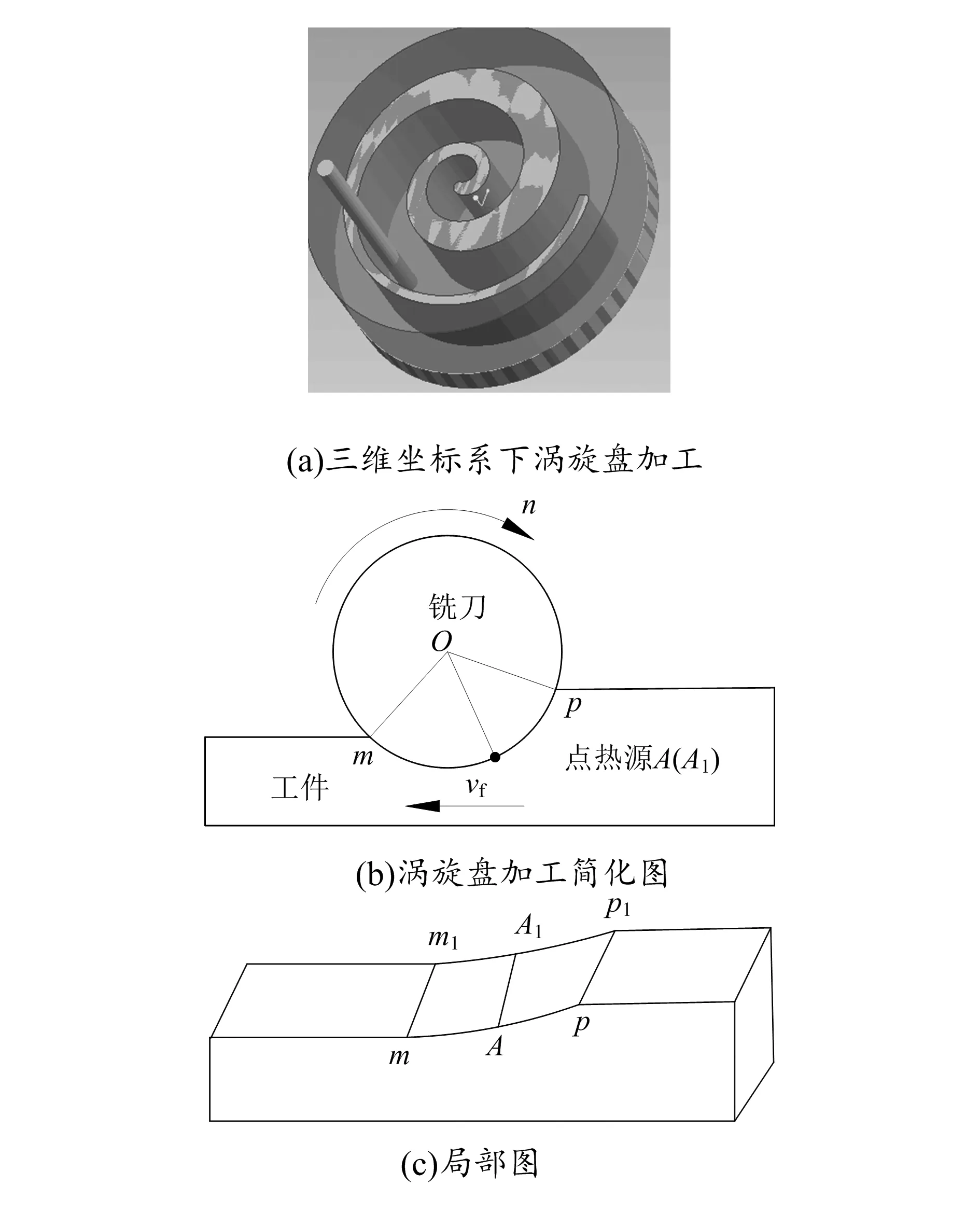
图3 涡旋盘加工模型示意图
假设在无限大物体内有一与y轴重合的无限长瞬时线热源(如图4所示),初始时刻t=0,线热源单位长度产生的热量为Q,随后立即消失。初始时刻除y轴外其余各点温度为零,根据文献[9]求出温度场计算公式为:
(4)
式(4)可以用来计算任何时刻、任何位置处在该点热源作用下的温升。

图4 无限长移动线热源示意图
本文的涡旋盘材料为Cr15Mo,其参数为:c=480J/(kg·℃),ρ=7 200kg/m3,k=39.2W/(m·℃),模拟在不同时刻工件上某一点热源产生的热量对x=z=20mm处的影响情况以及不同热源热量的温度差值,如图5所示。

图5 温度随时间变化曲线
从图可以看出,一定位置处,不同的热源热量Q引起的起始温度不同,随着时间的推移,温度先升高后降低,热源热量越大温度升高越快,在20s时两者温度差达到最大值208℃,20s后温度值降低,差值也越来越小。
3 剪切区温度和应力的变化
根据J-C本构模型,剪切面剪应力σs[10]为:
(5)

根据文献[11]得到剪切面的温度为:
(6)
(7)
式(7)是一个关于Ts和m的方程,m的值不同,所得到的Ts的表达式也不同。比如,当m=1时:
(8)
(9)
剪切面的温度数学模型,表明了在不同转速作用下,剪切区的温度变化与剪切应力σs、转轴转速n、切削速度v、切削深度h、工件材料有关。涡旋盘材料Cr15Mo的应力σs=4 200MPa,剪切应变γ=0.84,设定切削深度h=0.5mm,模拟不同主轴转速下剪切面的温升情况,结果如图6所示。
从图6可以看出,当主轴转速为8 000r/min时,剪切面的温度为753.978℃,主轴转速每升高1 000r/min, 剪切面的温度升高0.01℃。对于高速切削加工来说,当主轴转速大于8 000r/min时,剪切面的温度在754℃左右,而且随着主轴转速的增加剪切面的温度上升缓慢,这主要是因为高速切削过程产生的切削热大部分被切屑带走,工件的温度升高不明显,这也是高速切削加工涡旋盘有利于减小工件热变形的主要原因。

图6 主轴转速对剪切面温度的变化曲线

图7 不同应变下的应力-温度关系曲线

图8 不同温度下的应力-应变关系曲线


表1 铣削参数对剪切应力、应变及剪切温度的影响
从表1可以看出,在切削宽度ac不变的情况下,主轴转速为7 000r/min时,切削温度基本保持在753.957℃左右,此时涡旋盘温升缓慢。随着切削速度v的增加,剪切应变率每升高213/s,剪切应力大约增加20MPa。因此涡旋盘的加工要选择较高的主轴转速和适当的铣削参数,有助于减小切削温度和剪切应力、应变,有效地控制涡旋盘的热变形,提高涡旋盘的加工质量。
4 结论
本文对变截面涡旋盘高效、高精和高可靠性加工中的热变形问题进行分析,得出如下结论:
1)利用无限大线热源模型,得出在x=z=20mm处由不同热源热量引起的温度随时间的变化为先增高后降低,在20s时温度达到最大值,此时温差也达到最大值为208℃,随着时间的推移,温差逐渐减小。
2)利用J-C本构模型和剪切面温度场模型,推导出了剪切温度和剪切应力的数学模型。数值模拟表明:剪切温度随着主轴转速的增加而升高,同一温度下应力在大应变状况下要比小应变状况时显著,同一应变下剪切应力在低温状态下比高温状态下大。
3)当数控机床主轴转速达到7 000r/min时,切削温度基本保持在753.957℃左右,转速每升高1 000r/min,涡旋盘应变变化213/s,应力约增加20MPa。
[1] LOEWEN E G,SHAW M C. On the analysis of cutting-tool temperatures[J]. Trans.of the ASME,1954(2):217-231.
[2] SHAW M C. Mental Cutting Principles[M]. New York: Oxford University Press,1984:276-278.
[3] 关立文, 杨亮亮, 王立平,等. “S”形试件间歇性切削温度场建模与分析[J]. 清华大学学报(自然科学版), 2016(2):192-199.
[4] 刘胜. 钛合金正交切削的温度场和切削力仿真与试验研究[D]. 南京:南京航空航天大学, 2007.
[5] 姜芙林. 高速断续加工过程工件及刀具瞬态切削温度的研 究[D]. 济南:山东大学, 2015.
[6] JING F, LIU Z, WAN Y, et al. Analytical modeling and experimental investigation of tool and workpiece temperatures for interrupted cutting 1045 steel by inverse heat conduction method[J]. Journal of Materials Processing Technology, 2013, 213(6):887-894.
[7] 许兆美, 汪通悦, 裴旭,等. Al2O3陶瓷激光多道铣削温度场有限元模拟[J]. 红外与激光工程, 2015, 44(2):477-481.
[8] 阎海鹏. 高速铣削铝合金切削温度的研究[D]. 南京:南京理工大学, 2004.
[9] 李明艳. 高速切削温度场的有限元数值模拟[D].青岛:山东科技大学, 2005.
[10] 刘战强, 吴继华, 史振宇,等. 金属切削变形本构方程的研究[J]. 工具技术, 2008, 42(3):3-9.
[11] 何宁.高速切削技术[M]. 上海:上海科学技术出版社,2012.

