无人艇的双桨双舵推力优化分配仿真

刘梦佳， 冯 辉， 徐海祥

(武汉理工大学 a.交通学院, b.高性能船舶技术教育部重点实验室， 湖北 武汉 430063)

0 引 言

推力分配作为双桨双舵无人艇系统重要技术环节，主要根据上层控制器所要求的待分配力和力矩计算出各个推进器、舵的推力和舵角，从而使船舶到达预定位置和方向。推力分配可以被定义为以推进器本身推力大小、舵角大小和推进器之间的水动力干扰等约束为前提，寻找推进系统最小能耗的组合优化问题。

关于推力分配问题的求解，国内外学者做了大量的工作，但主要是针对动力定位船等过驱动系统，而且多半是研究多全回转推进器的优化策略和优化算法，针对主推带舵的推力分配优化方面较少。在国内研究方面，袁伟等[1]主要针对动力定位系统中的推力分配问题，对舵、桨组合的推力进行建模，将舵、桨组合的非凸推力区域转化成4个凸区域，将分析非线性最优化问题转换为线性最优化问题，但计算模型仅适用于低速船，不适用于高速艇。邵兴悦等[2]针对飞机控制系统的推力优化分配中的三维目标转矩问题，采用基于直接分配方法的邻近点搜索法，对飞机控制系统的三维推力和力矩进行推力分配优化，但这种方法不适用于二维的无人艇系统。许林凯等[3]针对船舶快速推进器，对动力定位的非凸问题进行凸化处理，采用增广拉格朗日乘子法对控制力进行优化分配。徐海祥等[4]采用直接分配算法，对全回转推进器和侧推在低速船中应用进行了推力分配优化。刘洋[5]采用改进的粒子群算法，对船舶推力分配作了仿真计算。文献[6]—[8]采用序列二次规划数学方法进行推力分配计算，但序列二次规划法不适用于推力系数矩阵B为非正定的情况。文献[9]针对序列二次规划法的缺点，设计自适应动态规划的训练和求解步骤，并采用RBF神经网络实现了该算法。文献[10]提出一种基于能量最优的推力分配优化算法，把优化问题分成静态和动态问题进行分析。文献[11]将桨、舵组合拆分为2个独立工作的等效推进装置，采用模拟退火算法进行求解。在国外研究方面， MILLAN[12]对动力定位船舶的艏向最优进行权重分配，但其推进模型为全回转推进器和侧向推进器，不适用于多桨、舵的无人艇推进系统。JOHANSEN 等[13]对带舵的推力分配问题进行建模，但其采用的舵力计算模型仅适用于低速船，不适用于高速艇。

综上所述，针对无人艇的双桨双舵模型或者多桨多舵模型，目前国内学者鲜有研究，主要采用同一控制信号进行输入来推进船舶航行。由于在推力分配方面不仅须考虑桨的推力分配问题，还须考虑舵推力模型，将舵力与螺旋桨推力模型进行组合，采用基于水动力特性的舵力计算模型，建立适用于无人艇系统的推力优化分配模型。

基于变速的双螺旋桨双舵模型，提出在舵角和推力限制条件下，采用fmincon函数目标推力进行优化分配。为验证所采用方法的有效性，对装有可变速螺旋桨的无人艇进行推力优化分配仿真。

1 推力分配概述

为达到更好的推力分配优化效果，无人艇的推进系统须满足2个要求：一是推力和力矩大小应能抵消预计的各种外力与力矩之和；二是推进器应该有快速的动态响应速度，以便对外力的变化迅速做出反应。

无人艇系统由滤波器、路径控制器和推力分配组成，如图1所示。滤波器剔除干扰信号，将估计后的无人艇位置和艏向信息传动给控制器，减少推进器的磨损和能耗。路径控制器根据目标位置和艏向的计算值与当前滤波器估计值之差，计算出无人艇航行到预定位置和艏向所需要的力和力矩。推力分配是无人艇系统中至关重要的部分，其主要功能是接收无人艇路径控制器所计算出的力和力矩，包括纵向力、横向力和艏向回转力矩，通过推力分配优化算法对其进行优化，将优化后的螺旋桨推力和舵角分配给各个螺旋桨和舵机，电机和舵机根据推力分配的指令运转，使艇航行到预定的位置和艏向。

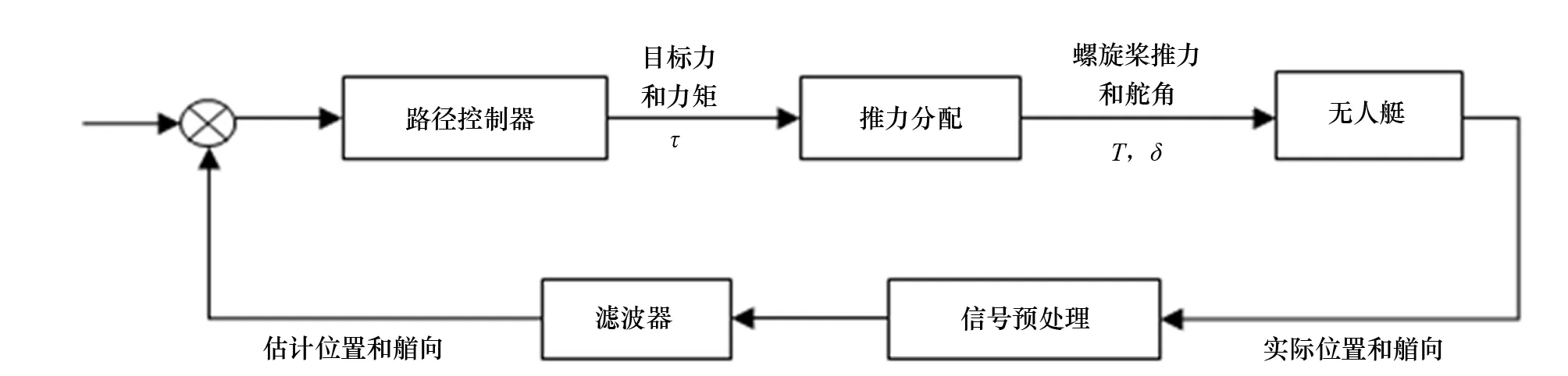
图1 无人艇系统原理

在一般情况下，无人艇系统中只考虑3个方向的运动：横荡、纵荡、艏摇3个自由度。在无人艇航行过程中，只有当螺旋桨发出的总推力为正向推力时，舵才产生有效升力，螺旋桨和舵组合的推力矢量成扇形区域；当螺旋桨发出的总推力为负向推力时，舵效几乎为零，推进器组合的推力矢量为1条直线[11]。因此，螺旋桨和舵组合的有效推力区域是非凸的，对研究无人艇推力分配而言是十分复杂的。桨、舵组合推进系统的可执行推力区域如图2所示。

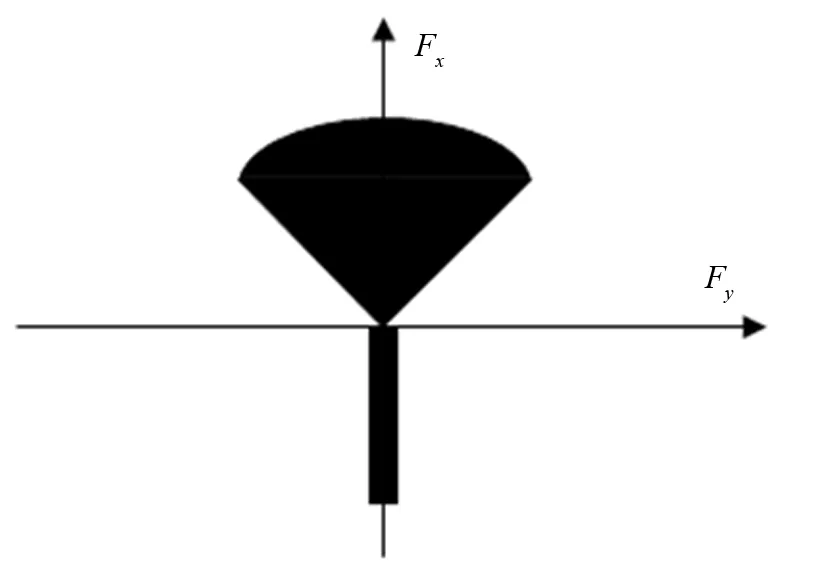
图2 桨、舵组合推进系统的可执行推力区域

2 数学模型

在建立推力分配计算模型方面，分别对单舵力计算模型、双桨双舵数学模型进行分析。

2.1 单舵力计算模型

舵力的计算模型与舵的舵叶面积、展弦比、来流攻角和来流速度相关，舵力分析如图3所示，FN为舵上的法向力，可采用藤井公式计算：

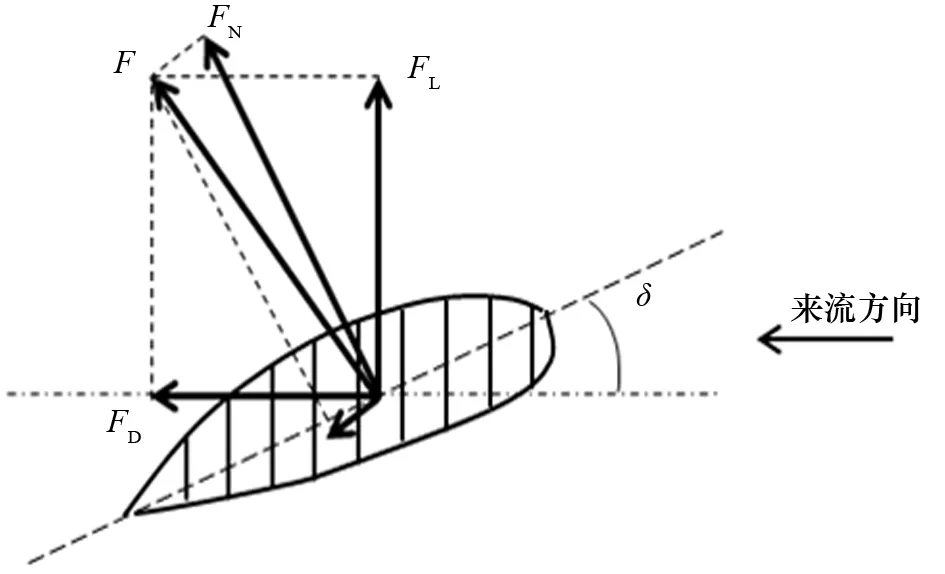
图3 舵力分析示意图

(1)

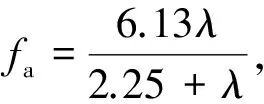
舵力和力矩可用式(2)进行计算：

(2)

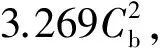
2.1.1 螺旋桨尾流影响

在一般情况下，舵的水动力特性在很大程度上由螺旋桨尾流场决定。当舵处于螺旋桨尾流之中时，螺旋桨尾流的诱导速度有3个分量，即轴向、切向和径向。诱导速度较小，可忽略。由于轴向诱导速度使流向舵的流速增加，切向诱导速度引起舵的有效冲角变化，则舵处的相对流速UR和相对水流冲角αR的经验计算公式为

(3)

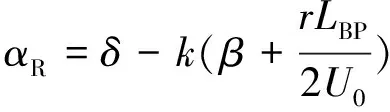
(4)

式中：K，ε为推力计算系数，K=0.68,ε=0.87;UP为螺旋桨进速；J为螺旋桨进速系数，J=UP/(nD)，其中n为螺旋桨转速，D为螺旋桨直径;KT为螺旋桨推力系数；k为整流系数；r为艏摇角速度；β为漂角；LBP为船舶的垂线间长；U0为船舶航速。

2.1.2 不考虑螺旋桨尾流影响

如果不考虑螺旋桨尾流影响，舵处的相对流速UR经验计算公式为

UR=(1-ωR) ·U0

(5)

式中：ωR为舵处的伴流系数；U0为船速。

2.2 双桨双舵的数学模型

根据无人艇船体布置图，建立无人艇双桨双舵的组合推力数学模型，如图4所示。根据舵力计算公式，舵力与螺旋桨推力有关[11]。当螺旋桨发出正向推力时，舵受前方螺旋桨产生的来流影响会产生有效舵升力，如图4a)所示；而当螺旋桨发出负向推力时，舵不产生有效升力，如图4b)所示。

螺旋桨推力的计算模型可简单表示为

T=kT|ω|ω

(6)

式中：T为定轴螺旋桨推力；ω为螺旋桨旋转角速度；kT为定轴螺旋桨推力系数。

在如图5所示的无人艇推进器布置图中， 设船舶的重心坐标为(xG,yG) ，螺旋桨的位置坐标为(-x1,y1),(-x1,-y1)，舵的位置坐标为(-x2,y2)，(-x2,-y2)，T1和T2分别为左、右螺旋桨的推力。根据螺旋桨、舵推力计算公式和位置分布，可建立双桨双舵推力分配模型为

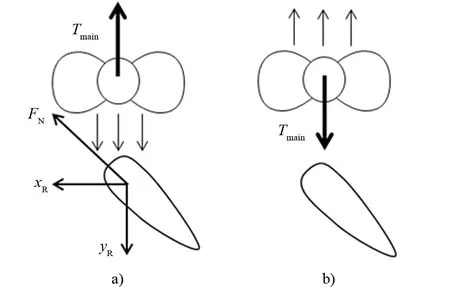
图4 主推和舵组合示例

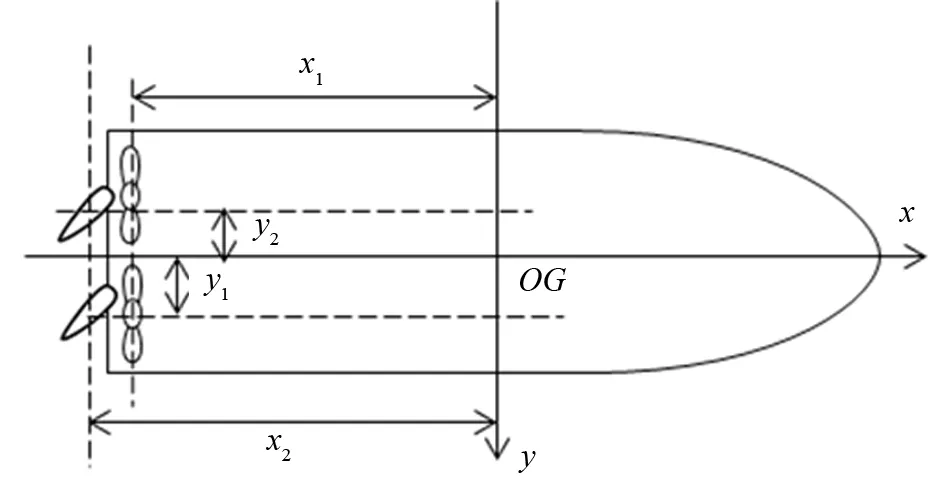
图5 无人艇推进器布置图

Fx=T1+T2+xR1+xR2

(7)

Fy=yR1+yR2

(8)

Nz=T1y1-T2y1+NR1+NR2+xR1y2-xR2y2

(9)

式中：Fx,Fy和Nz分别为纵向推力、横向推力和转艏力矩。

综合上述计算模型，可得到无人艇系统的推力分配模型为

τ=BT

(10)

目标可达力和力矩为

τ=[τ1,τ2,τ3]T

(11)

无人艇桨和舵的推力为

T=[T1,T2,FN1,FN2]T

(12)

系数矩阵B为

(13)

3 推力分配优化算法

针对桨和舵所产生的推力矢量与桨发出的推力正负相关的情况，对螺旋桨的推力之和进行不等式约束，同时在处理时根据上文所建的数学模型将桨和舵的推力进行分开处理，如图6所示,图6a)为舵的推力可执行区域，图6b)为定轴螺旋桨的推力可执行区域。

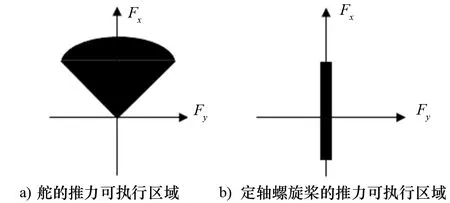
图6 桨、舵可执行推力区域

无人艇推力系统的推力分配属于单目标、多约束、非线性、非凸的优化问题，从目标函数、约束条件等方面对该问题进行详细描述。

3.1 目标函数

无人艇的工作要求不同，其优化目标函数的选取也不同，主要从无人艇能耗、操纵性、推进器磨损、奇异性等方面进行考虑[3]。以无人艇能耗最少和推力误差尽量小为目标，建立目标函数如式(14)所示。

(14)

3.2 等式约束

推进器推力和控制力之间的关系可表示为对纵向力、横向力和转艏力矩等3个自由度上的约束等式为

(15)

3.3 不等式约束

在推力分配过程中，不仅须充分考虑螺旋桨和舵推进能力的限制，包括最大推力和最大舵角，还须考虑螺旋桨和舵的实际推力的机械特性限制[2]。由于螺旋桨以及舵机转速的限制，为避免推力和角度变化率较大引起的推进系统过度磨损，设置推力变化率和角度变化率的不等式约束。

对推力变化和舵角变化采用动态约束，式(16)分别为定轴螺旋桨推力的动态约束与舵角的动态约束，参考文献[3]同时在式(17～18)中给每个采样时刻具体的推力大小和舵角范围，保证螺旋桨的合力状态为正，使舵力为有效状态。

(16)

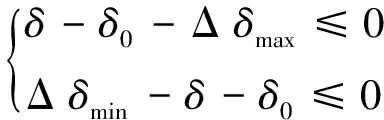
(17)

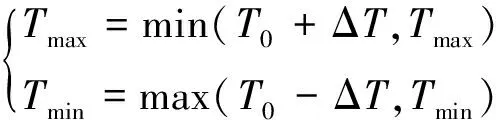
(18)

式中：Tmax与Tmin分别为螺旋桨在当前状态下考虑推力变化率后推力的上限和下限；ΔT为推进器的推力变化率；T0为推进器上一控制周期所发出的推力；δ为当前控制周期舵角；δ0为上一控制周期舵角；Δδmax和Δδmin分别为舵角度变化率上限和下限。

考虑到目标函数的非线性、等式约束和不等式约束的非线性，同时考虑到无人艇作为快速艇对计算时间的要求，主要采用MATLAB中的fmincon函数进行推力优化分配计算。

fmincon函数适用于非线性目标函数，主要适用于下面约束条件的优化：

minf(x)

(19)

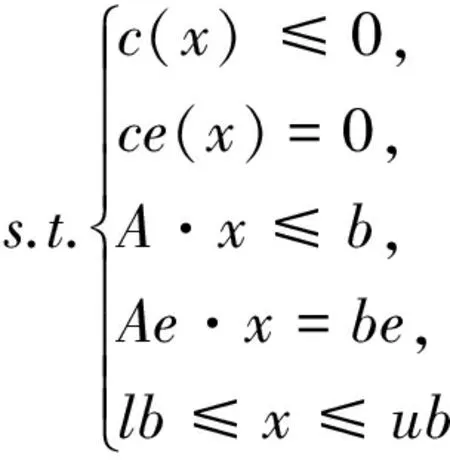
(20)

式中：x为变量；A和Ae为线性不等式约束和等式约束的系数矩阵；f(x)为目标函数；b,be,lb和ub为变量x的线性不等式约束下界和上界向量。

4 算例仿真分析

4.1 仿真参数

采用的仿真模型为双桨双舵的无人艇模型，船长为1.0 m，船宽为0.25 m，型深为0.08 m，装有2个电机及电机驱动器、1台舵机。因此，只能发出1个舵角信号，将双舵角处理为1个舵角输出，则舵的纵向力所产生的转矩可互相抵消。为避免失速现象，舵角保持在≤±35°，操舵速度≤±2.34 (°)/s，船速为1.25 m/s。螺旋桨和舵的具体参数如表1所示。

表1 螺旋桨和舵参数

螺旋桨尾流对舵力影响较小，故采用不考虑螺旋桨尾流的计算公式。根据舵力计算公式，对应舵力参数的取值如表2所示。

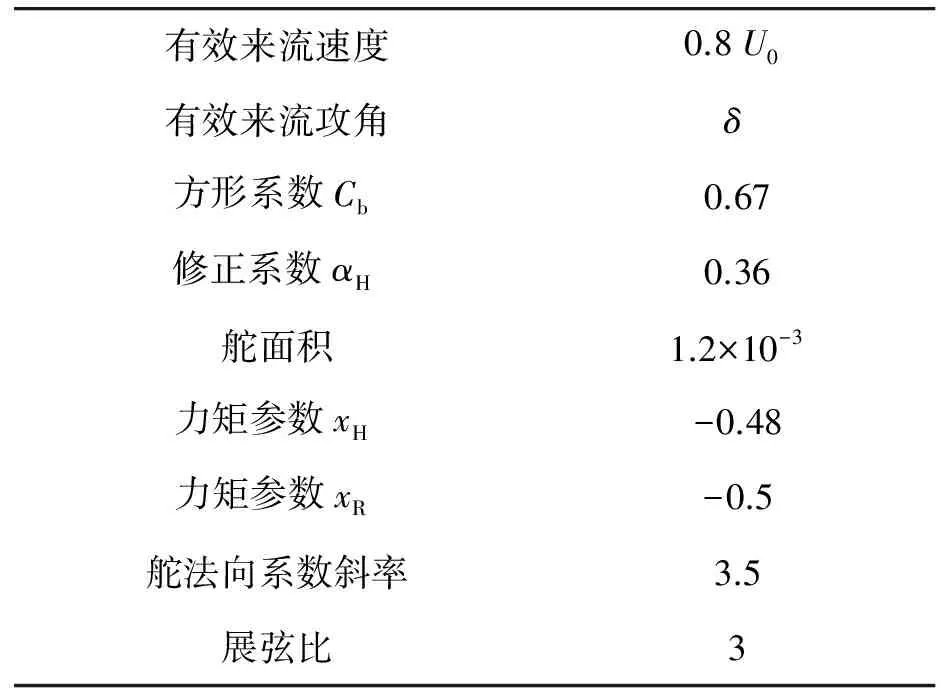
表2 舵力参数取值

代入参数得到舵力及推力系数矩阵B的表达如式(21)和式(22)所示。

FN=2.1×sinδ

(21)

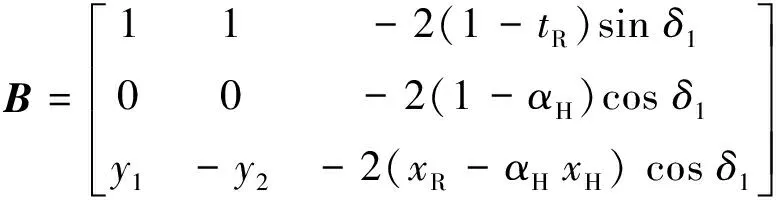
(22)

目标力和力矩的取值如式(22)所示。

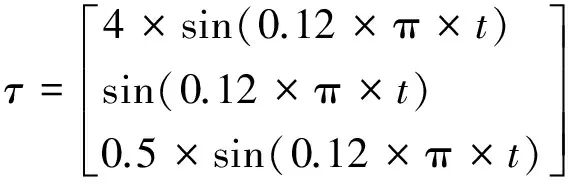
(23)

4.2 仿真结果

4.2.1 不考虑舵角及推力变化率

采用fmincon函数进行推力分配仿真计算，得到计算结果如图7所示。

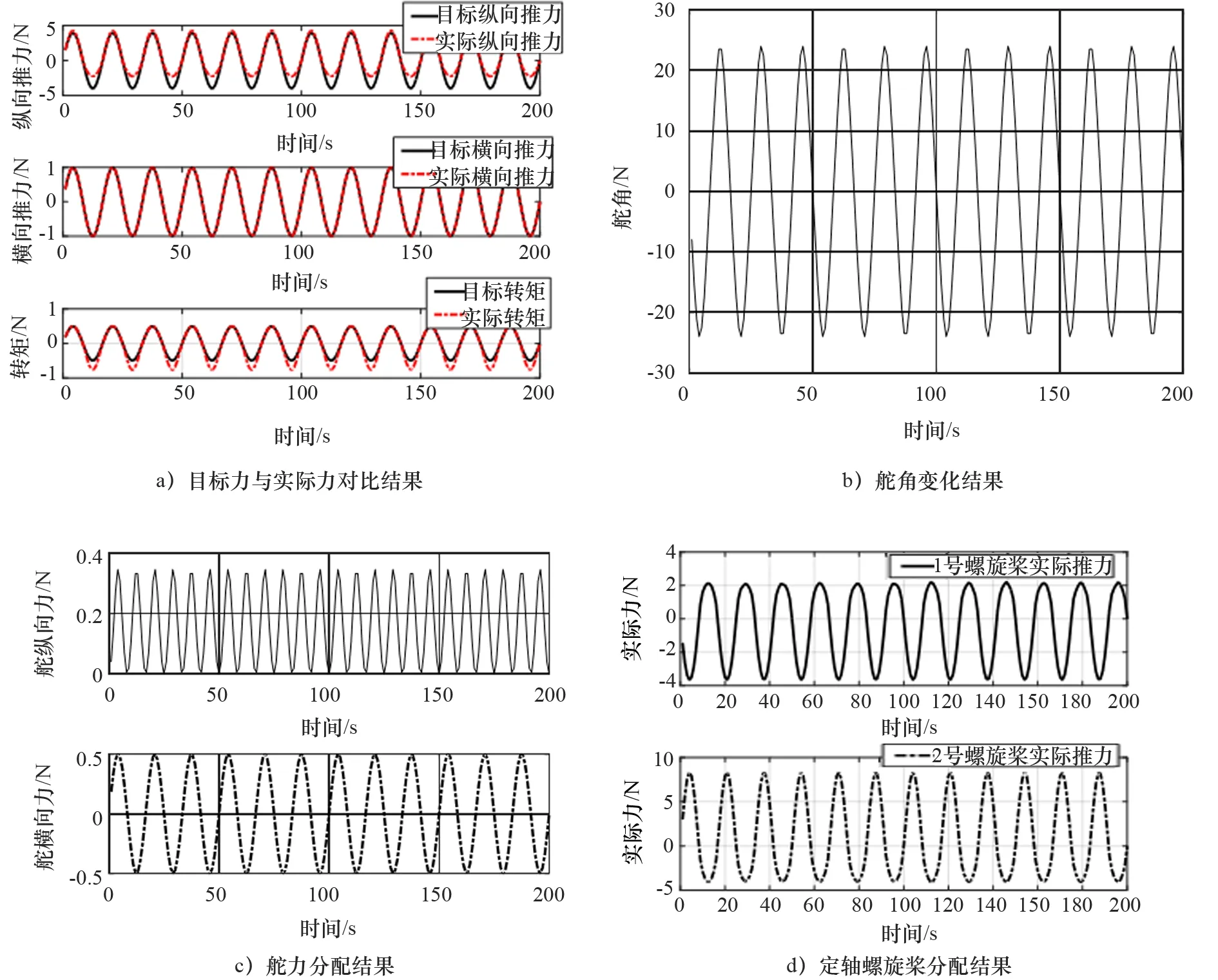
图7 推力分配计算结果

4.2.2 考虑舵角及推力变化率

根据舵角变化率的限制，对力和力矩目标函数进行修改，采用的目标力矩值如式(24)所示，得到仿真计算结果如图8所示。

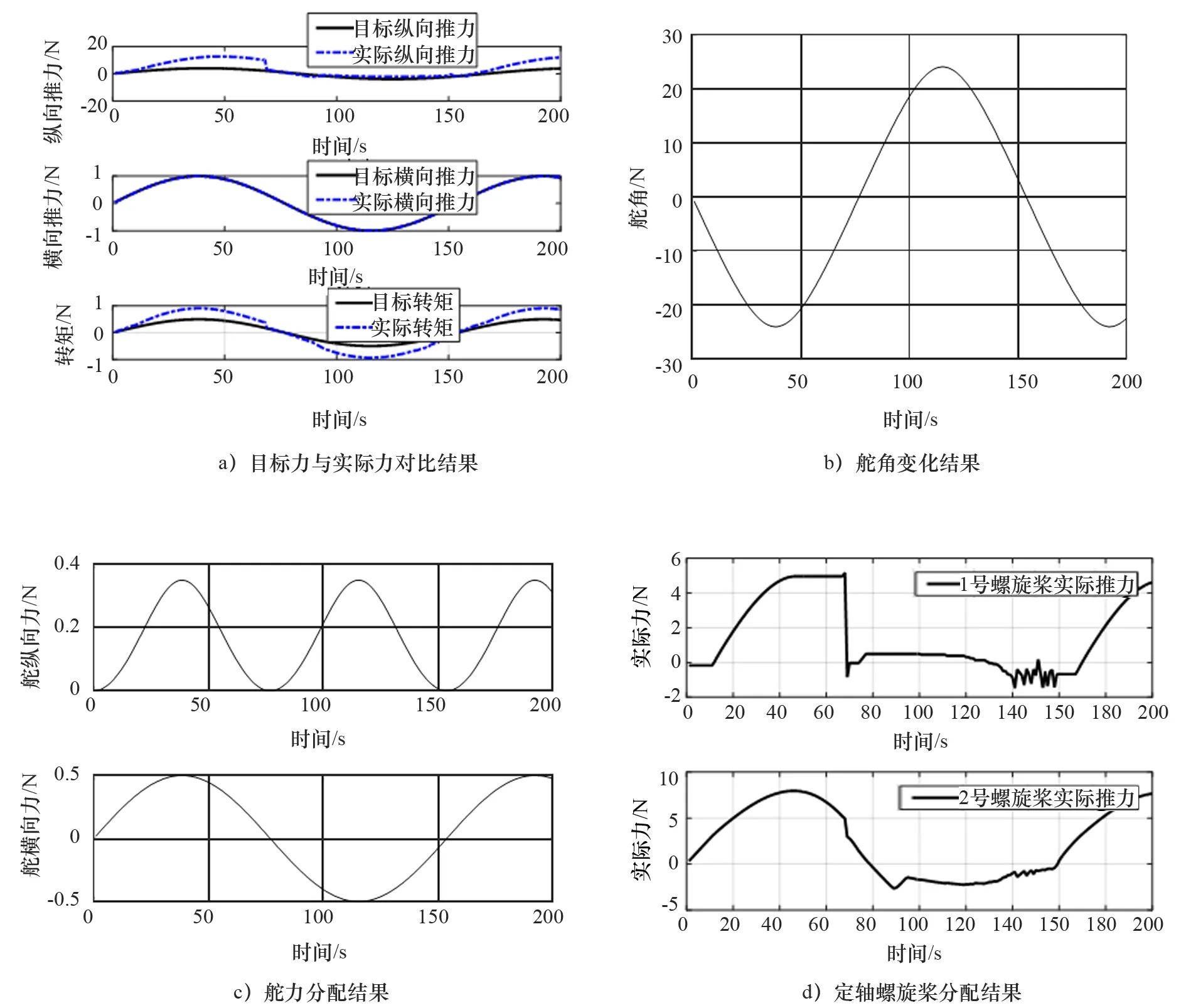
图8 变化率约束下的推力分配仿真结果

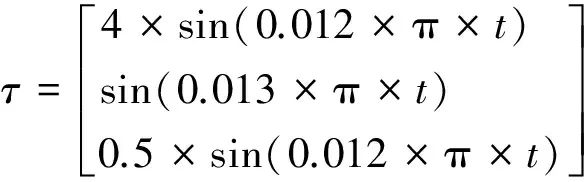
(24)

从2次试验结果可以分析得出，fmincon函数在求解非线性等式和不等式约束的推力分配问题方面有较强的求解效果，且运算时间短，适合高速无人艇。在进行仿真运算时，给定1组关于时间t的目标力和力矩函数，舵角变化与目标函数的频率设置有关，为达到角度变化率的要求，在设置目标函数时，要对其进行改进，改动后的目标力和力矩如式(24)所示。图7a)和图8a)分别是2次推力分配仿真结果，从计算结果可以得到实际分配的横向力和纵向力及力矩值基本与目标值一致，图8a)存在目标纵向力与实际纵向力偏差；图7b)和图8b)舵角的变化结果，较好地符合实际舵角要求。图7c)和图8c)是舵横向力和纵向力的仿真结果。图7d)和图8d)是2个定轴螺旋桨的推力分配计算结果，由于推力变化率限制，推力变化较剧烈，但基本在要求范围之内。从2次仿真计算结果可以得到，使用fmincon函数可以较好地得到螺旋桨和舵的推力，与目标力和力矩函数近似一致，且运算速度快，适用于高速无人艇的推力分配计算要求。

5 结 论

在无人艇系统中，对桨、舵组合模式的推进系统进行推力分配仿真计算，有助于提高推进效率和推力利用率。针对桨、 舵组合造成推进器有效推力为

[][]

非凸推力区域问题，把桨、舵的推力分开进行处理，同时建立双桨双舵的推力计算模型。考虑到定轴螺旋桨和舵机的机械特性，在推力分配建模中引入推力变化率和舵角变化率约束，并采用适用于非线性约束优化推力分配问题的fmincon函数进行求解，经过仿真计算，结果证明该推力分配方法的有效性，显著地减少无人艇推进系统的能耗并且可用于配置桨、舵组合的其他类型高速无人艇中。

[ 1 ] 袁伟,俞孟蕻,朱艳. 动力定位系统舵桨组合推力分配研究[J]. 船舶力学,2015(4):397-404.

[ 2 ] 邵兴悦, 任章, 廉成斌. 三维目标直接分配新算法[J]. 中南大学学报(自然科学版), 2013(S2):385-390.

[ 3 ] 许林凯, 徐海祥, 李文娟,等. 快速转向推进器推力优化分配研究[J]. 海洋工程, 2015, 33(2):13-20.

[ 4 ] 徐海祥, 付海军, 冯辉. 动力定位直接分配算法及其仿真[J]. 大连海事大学学报, 2016, 42(2):23-27.

[ 5 ] 刘洋. 船舶动力定位的智能控制及推力分配研究[D]. 大连：大连海事大学, 2013.

[ 6 ] 郭鹏威. 半潜船动力定位系统推力分配仿真研究[D]. 武汉：武汉理工大学, 2012.

[ 7 ] 金超. DP系统的推力分配优化算法研究[D]. 哈尔滨：哈尔滨工程大学, 2013.

[ 8 ] 吴显法, 王言英. 动力定位系统的推力分配策略研究[J]. 船海工程, 2008, 37(3):92-96.

[ 9 ] 张晓迪. 船舶推力分配多步优化算法研究[D]. 上海：上海交通大学, 2015.

[10] 王钦若, 杨娜, 叶宝玉,等. 船舶动力定位系统推力分配策略研究[J]. 控制工程, 2013, 20(1):30-33.

[11] 刘正锋, 孙强, 江伟,等. 航行作业船舶考虑舵力的动力定位能力评估方法研究[J]. 船舶力学, 2016, 20(4):439-445.

[12] MILLAN J. Thrust Allocation Techniques for Dynamically Positioned Vessels [J]. Laboratory Memorandum, 2008.

[13] JOHANSEN T A, FUGLSETH T P, TФNDEL P, et al. Optimal constrained control allocation in marine surface vessels with rudders [J]. Control Engineering Practice, 2007, 16(4):457-464.