基于短时傅里叶变换的纺织材料纤维取向度测量方法

张 芳 ，田红霞 ，肖志涛 ，王 雯 ，庄旭品

（1.天津工业大学 电子与信息工程学院，天津 300387；2.天津工业大学 天津市光电检测技术与系统重点实验室，天津 300387；3.天津工业大学纺织学院，天津 300387）

纺织材料是纤维材料直接构成的纤维集合体，纤维的取向分布会影响纺织材料的物理和机械性能.为了观察纤维的取向，常借助高倍放大的扫描电子显微镜.基于扫描电镜图像，人们提出了相关的取向度测量方法，目前主要有直接追踪法[1-2]、流场分析法[3-4]和傅里叶变换法[5-10].直接追踪法利用细化和轮廓增强技术，把实际图像中的纤维转化成简单数字化的弧线，这些弧线为原图像纤维的中间轴.但考虑到计算的准确率，需要对纤网进行薄化处理，这就大大增加了工作量.流场分析法提取图像灰度梯度的取向信息，根据纤维的取向与灰度梯度矢量的方向相互垂直的原理计算纤维取向度.该方法简单易实现，但计算结果容易受到图像噪声的影响.傅里叶变换法是把图像的灰度强度分布分解成具有一定振幅和相位的频率分布，根据纤维图像的频谱得到纤维的取向度.但是采用傅里叶变换法的前提是原始图像是周期图像，当图像并不完全是周期性的或者图像的不同区域存在较大差异时，频率图中会有很多错误的频率成分，即产生边界效应，这必然会对取向度的测量产生很大影响.

针对以上方法的不足，本文提出了一种基于短时傅里叶变换的纺织材料纤维取向度测量方法，把纤维图像看作总体非平稳、局部平稳的信号[11]，采用中间平坦、四周衰减的窗函数对局部平稳区域进行短时傅里叶变换，通过频谱分析测量纤维的取向度.本方法既可以改善频谱图的边界效应，也可以避免对全局图像直接处理而忽略细节的问题.

1 图像的傅里叶变换

傅里叶变换法广泛应用于图像分析中，以图像中灰度变化作为处理对象的依据，把图像数据由空间域变换到频域中，其物理意义是将图像的灰度分布函数变换为图像的频率分布函数，然后在频域中分析图像的特征[12].其变换公式为：

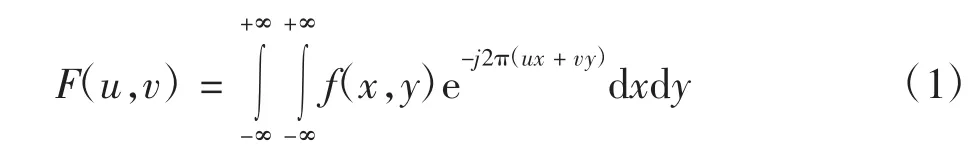
式中：f（x，y）为二维图像信号.

频域信号F（u，v）可以反映图像f（x，y）在时域中的灰度变化和图像结构.具有精细结构的图像其高频分量较丰富，在其傅里叶变换频谱图中灰度能量分布在离原点较远的位置；而当纹理较粗的情况下，其低频分量较丰富，在其傅里叶变换频谱图中灰度能量分布在离原点较近的范围内；当某纹理图像存在大量沿某方向的线、边缘时，则在频率域内能量集中出现在与该方向垂直的方向上；如果纹理没有表现出方向性，则频谱图像也不呈现方向性.

在应用傅里叶变换进行图像分析时有一个重要假设，即认为图像是周期性的，只有这样用离散傅里叶反变换得到的图像才能反映原始图像的真实规律.如果图像不是严格平稳的，也就是不能很好地满足周期性，在图像的边界处会出现不连续的现象，这样在功率谱图像中就会因为边界的不连续而含有一些错误的频谱成分，这必然会对取向度的测试产生很大的影响[13].短时傅里叶变换（short-time Fourier transform简称STFT）是在傅里叶变换的框架内，针对总体非平稳、局部平稳的信号而提出的一种频谱分析方法.通过在时域加窗函数，并通过一个平移参数使窗口平移覆盖整个时域，将原始图像这一非平稳信号转化为短时平稳信号，再对每个窗函数所覆盖的局域图像做傅里叶变换.对于给定的非平稳信号b（t），通过窗函数W（t）定义新的信号bt（τ）：

对新信号作傅里叶变换的结果称为原信号的短时傅里叶变换[14]，即：

针对二维图像I（x，y），对其施加窗函数W（x，y），则I（x，y）的二维短时傅里叶变换可表示为：

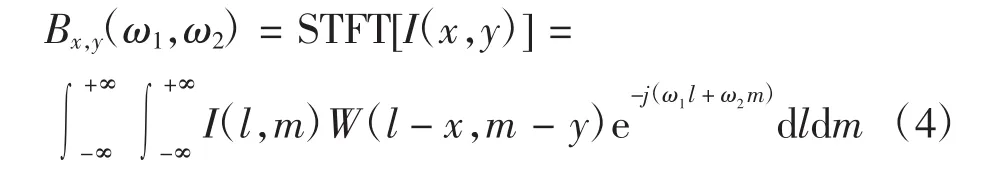
若对图像加窗后的各个子块建立独立的坐标系，可将上式简化为：

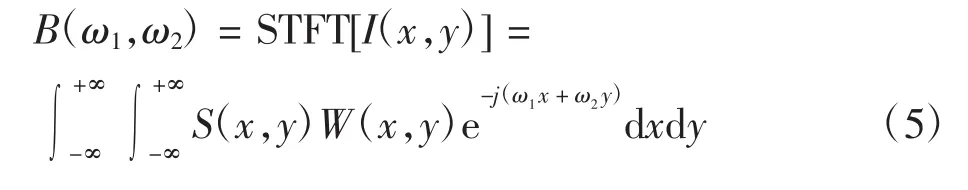
2 基于STFT测量纤维取向度

纤维图属于非平稳信号，不满足整体傅里叶变换的要求，因此本文采用短时傅里叶变换对纤维图像进行频谱分析.本文提出的基于短时傅里叶变换的纺织材料纤维取向度测量方法整体流程如图1所示.

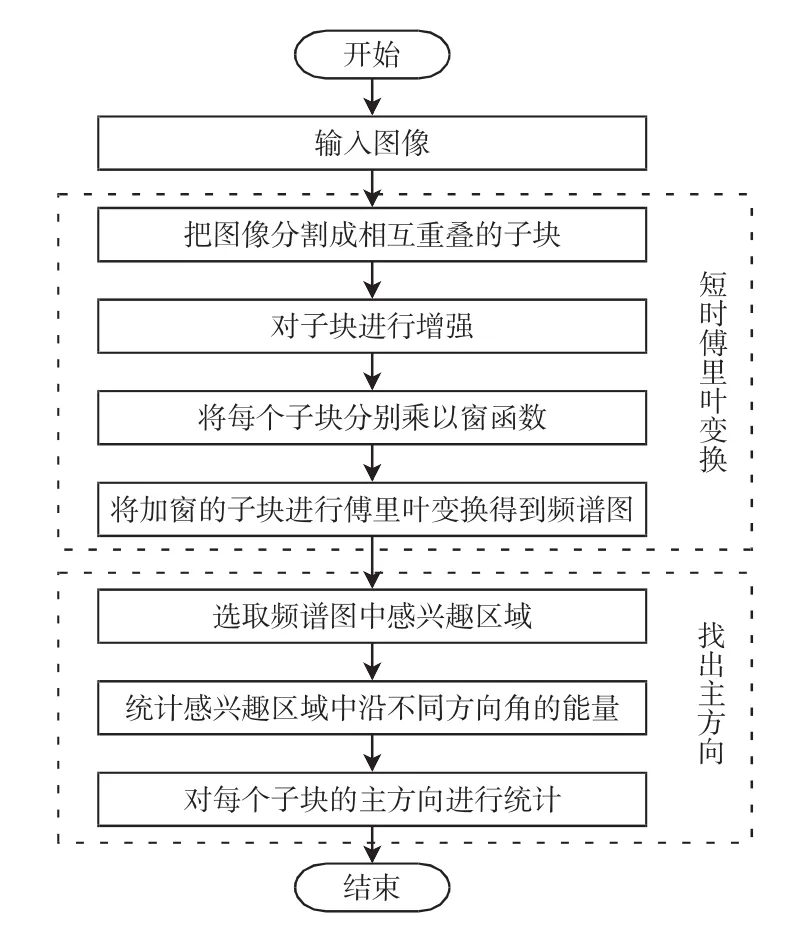
图1 测量方法的整体流程Fig.1 Overall flow chart of measurement method

主要步骤为：

（1）把纤维图像分成大小为M×M且相互重叠量为 N 的子块 S（x，y），并对每个子块 S（x，y）进行对比度增强；

（2）对每个子块 S（x，y）乘以窗函数 W（x，y），并对加窗的子块进行傅里叶变换得F（u，v）；

（3）选取每个子块的频谱图中的感兴趣区域，得到新的频谱图FS（u，v）；

（4）计算新的频谱图中沿不同方向角的总能量，并找出每个子块中纤维的主方向；

（5）对每个子块的主方向进行统计.

2.1 图像预处理

本文采用短时傅里叶变换通过对纤维图像加窗并使窗口平移覆盖整个时域，进而对纤维图像进行局部频谱分析.首先把纤维图像分成大小为M×M、重叠量为N的子块S（x，y）.其中窗口大小的选择应保证在子块内图像是平稳的，同时相邻窗口之间有一定的重叠信息，这样既能体现相邻点的相关性，也保持了信号的连贯性，避免块边缘效应.

原始图像中纤维目标与背景的对比度较差，因此本文采用对比度受限自适应直方图均衡化（contrast limited adaptive histogram equalization，CLAHE）方法来增强纤维图像的对比度.图2为纤维图局部区域及其增强图.

图2 纤维图局部区域及其增强Fig.2 Fiber image and its enhanced image

2.1.1 窗函数的选取

针对图2（b）所示图像，如果选取的窗函数W（x，y）=1，相当于取纤维图的一小块直接进行二维傅里叶变换，此时得到的频谱图如图3所示.图3中较亮的部分反映了时域图像中纤维的频率和方向.但是频谱图中在水平和竖直方向上，还有一些不规则的光痕，这就是边界效应.如前所述，造成边界效应的原因是由于傅里叶变换总是试图把图像分割成水平、竖直方向周期变化的两组单位图像的线性组合.由于纤维图像并非严格平稳的，即使将其分割为一系列小的子块，子块图像仍然不满足周期性，这样在频谱图像中就会因为边界的不连续而含有一些错误的频谱成分，这必然对取向度的测试产生很大影响.

图3 纤维图局部区域的频谱图Fig.3 Spectrogram of a local fiber image

为了减少边界效应对测量的不利影响，可通过加窗来尽可能减少在非整数个周期上进行FFT产生的误差.子块图像边界会呈现不连续性，加窗可减少这些不连续部分的幅值.加窗的结果是尽可能呈现出一个连续的波形，减少剧烈的变化.为了减少边界效应得到更为清晰的频谱图，本文采用中间平坦、四周衰减的窗函数.公式如下：

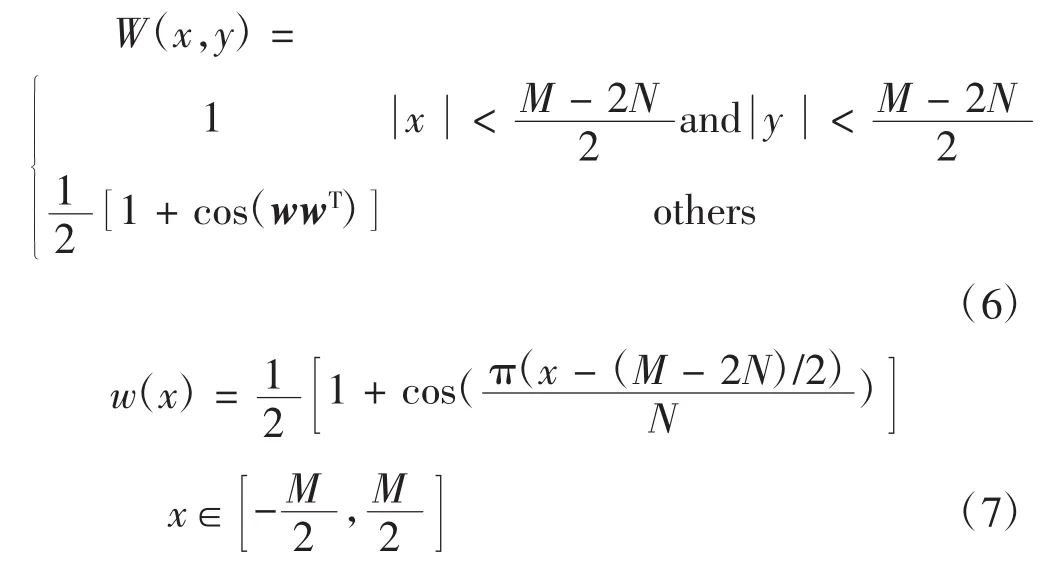
式中：M为子块大小；N为重叠量.

图4所示为窗函数.该函数的中心为平坦区域，四周快速衰减.由于仅在边界上有衰减，该窗函数能完整保留图像内部的大部分区域.图5显示了加入窗函数后对局部区域进行傅里叶变换后的频谱图.与图3相比，经过窗函数预处理的图像，变换后边界效应得到了明显改善.

图4 窗函数Fig.4 Window function

图5 加入窗函数后局纤维图部区域的频谱图Fig.5 Spectrogram of local fiber image with the window

2.1.2 子块的大小及重叠量

在本文方法中，子块大小及其重叠量对处理结果有重要影响.为了保证每根纤维都能被窗函数的平坦区域覆盖，而不会发生某一根纤维仅处在窗函数的衰减带的情况，子块重叠量至少等于单根纤维直径；同时重叠量也不宜过大，这样既增加运算时间又会因对某些纤维重复统计而影响最终的取向度结果.因此，本文选择子块重叠量为单根纤维直径.

本文利用不同角度、同周期和不同周期的模拟纤维图像对子块大小进行分析.图6展示了部分模拟图像.

图6 相同周期与不同周期的模拟纤维Fig.6 Simulated fiber image

通过大量实验发现，子块中非重叠区域必须包含2个以上的完整的亮条纹才能正确统计出条纹取向结果，所以在理想情况下窗口的非重叠区域须大于2倍纤维直径.再加上窗口四周的衰减带，即选取子块大小M至少应为4倍纤维直径.本文使用的纤维图是在放大20 000倍的情况下采集到的，单根纤维的直径约为20个像素，此时M应为80.

实际的纤维图分布不均匀，纤维局部区域图及对应的频谱图如图7所示.如果将子块大小M设为80，部分子块中将包含大量背景，如图7（a）所示，此时其频谱图如图7（b）所示.观察图7可以发现，子块中背景占据面积比较多时，子块的频谱图中边界效应非常较明显，这将严重影响最后的统计结果.因此在实际处理时，需要对子块进行扩展，使窗口中包含更多的纤维以消除背景对处理结果的不利影响.实验中以单根纤维直径为步长，逐渐增大子块大小，并统计子块中纤维部分的面积所占子块总面积的比例σ.图7列出了部分实验结果.统计发现，当σ大于45%时，子块频谱图中的边界效应可以得到有效改善.对于放大倍数为20 000的纤维图像，子块大小M=160时，即可满足上述要求.在满足要求的情况下，子块也不宜过大，过大的子块会包含更多的纤维，如果其中的纤维取向不一致，会丢失局部信息，影响最终的统计结果.所以本文最终选择M=160.

图7 纤维局部区域图及对应的频谱图Fig.7 Local regions of fiber and corresponding spectrum

2.2 对频谱图的操作

2.2.1 选取频谱图的感兴趣区域

对每个子块的频谱图进行二值化，选取其中的重要频率所占区域为感兴趣区域，然后进一步对感兴趣区域内的频谱成分进行分析，如图8所示.图8中白色区域为图5频谱图所对应的感兴趣区域.

图8 频谱图感兴趣区域Fig.8 Interesting area of spectrogram

2.2.2 感兴趣区域能量累加及纤维取向度确定

把子块的频谱由直角坐标系下的形式FS（u，v）表示成极坐标F（r，Θ）的形式，变换公式为：

式中：r、Θ分别表示频域图中某一点在极坐标系下的极径和极角.

然后将频谱图F（r，Θ）感兴趣区域中同一极角下的能量相累加，能量最大的极角为子块频谱图的主方向.根据傅里叶变换的特点可知，频谱图中频率变化方向与时域图中图像变化方向垂直.因此得到每个子块的频谱图的主方向后，可根据主方向得到时域图中相对应的方向，并据此统计出纤维的取向度.

3 实验结果与分析

为了验证本文方法的有效性，对模拟图像和实际采集的纤维图进行实验.首先模拟了不同方向、相同周期和不同周期的纤维图，实验结果如表1所示，其中正确的检测结果加粗显示.

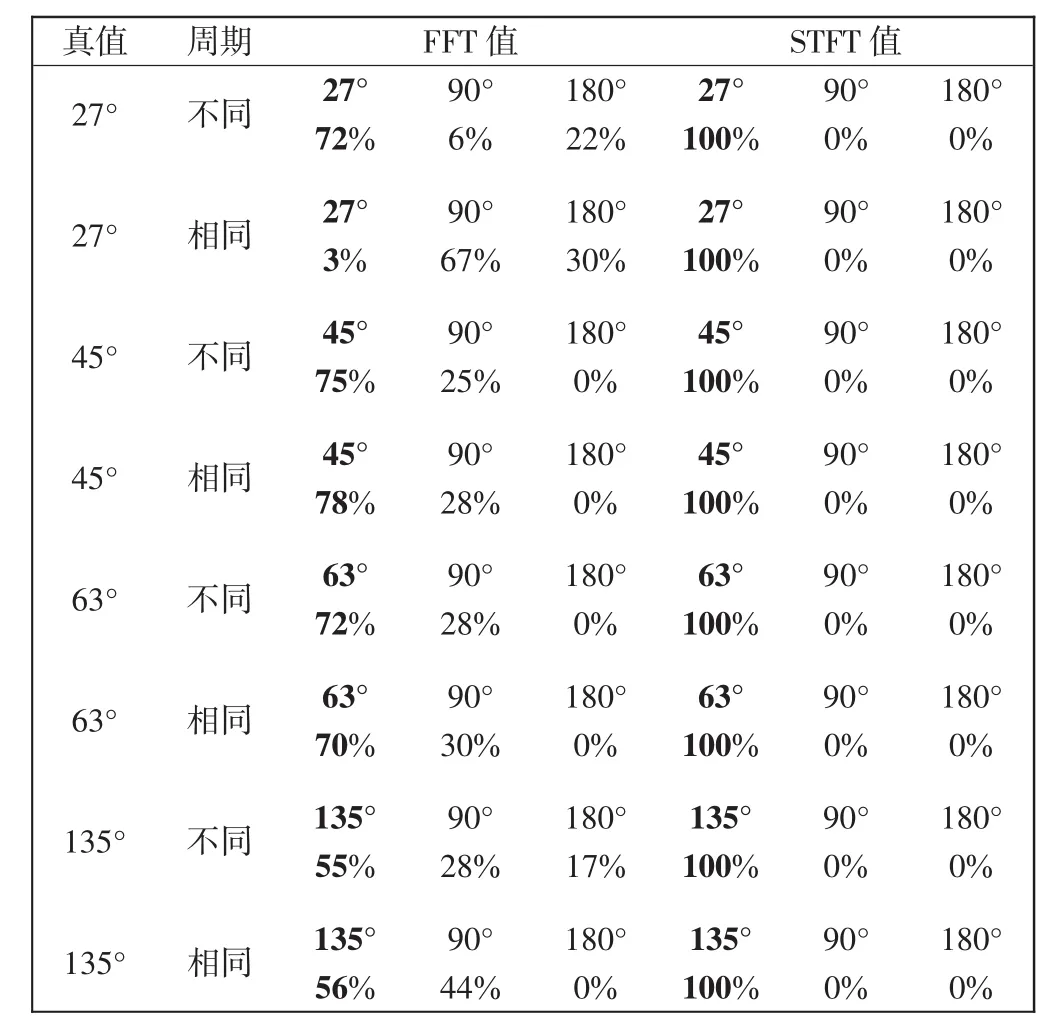
表1 模拟图的纤维取向分布Tab.1 Orientation distribution of the simulated fiber images

由表1可以看出，FFT实验值与真值比较误差较大，在错误的统计结果中90°方向和180°方向的比例比较大，这是由于边界效应导致在频谱图中出现了错误的频谱成分.而在STFT实验值中这2个方向的比例明显减少，即边界效应明显改善.实验表明，本文能准确地反映出模拟纤维图中纤维的取向分布.

图9为使用扫描电镜采集到的放大倍数为20 000的纤维图及其取向分布图，图中以5°为区间对纤维取向度进行了角度合并.

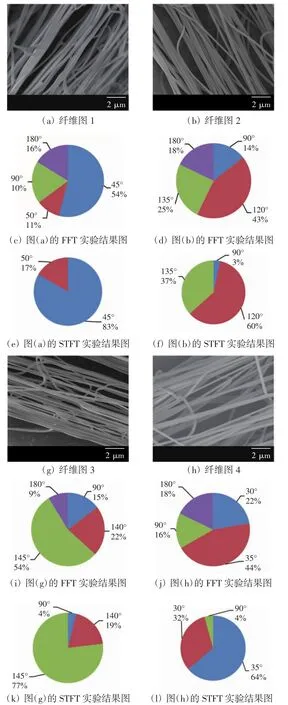
图9 放大倍数为20 000的纤维图及其取向分布Fig.9 Fiber images magnified 20 000 times and their orientation distribution

通过观察可以发现，FFT实验结果中有很多错误的频谱成分，其中90°和180°方向的纤维比例比较大，与实际情况不符，这说明FFT的边界效应比较明显；而本文方法得到的纤维取向分布图中90°和180°方向的纤维比例明显减少，定量结果表明，使用本文方法得到的测量结果与FFT方法的测量结果相比较，图9（a）至图9（h）的4个样本中90°方向纤维的比例分别减少 19%、11%、11%、18%，180°方向纤维的比例分别减少16%、18%、9%、18%.这说明本文方法能有效克服传统FFT方法的边界效应，统计结果更符合真实的纤维的取向分布.

4 结 论

由于纤维图是非平稳信号，本文提出了一种基于短时傅里叶变换的纺织材料纤维取向度测量方法.把纤维图像看作总体非平稳、局部平稳的信号，采用中间平坦、四周衰减的窗函数对局部平稳区域进行短时傅里叶变换，通过频谱分析测量纤维的取向度.本方法既可以改善频谱图的边界效应，也可以避免对全局图像直接处理而忽略细节的问题，从而提高测量的准确性.对4个样品的测试结果表明，使用本文方法得到的测量结果与传统的FFT方法测量结果相比较，90°方向的纤维比例平均减少14.75%，180°方向的纤维比例平均减少15.25%.

[1]王丽.基于图像处理的非织造布纤维直径与取向分布的测量[D].上海：东华大学，2008.WANG L.The measurement of the fiber diameter and orientation distribution of nonwoven fibrics based on image processing[D].Shanghai：Donghua University，2008（in Chinese）.

[2]GONG R H，NEWTON A.Image-analysis techniques part II：The measurement of fibre orientation in nonwoven fabrics[J].Journal of the Textile Institute，1996，87（2）：371-388.

[3]BRESEE R R，DANILUK T S.Characterizing nonwoven web structure using image analysis techniques[J].Tappi Journal，1997，80（7）：133-138.

[4]HEARLE J W S，STEVENSON P J.Nonwoven fabric studies:PartⅢ：Theanisotropyofnonwoven fabrics[J].TextileResearch Journal，1963，33（11）：877-888..

[5]金春奎，仲岑然.傅里叶变换在纳米纤维取向测量中的应用[J].纺织学报，2013，34（11）：34-38.JIN C K，ZHONG C R.Use of Fourier transform in measurement of nano-fiber orientation[J].Journal of Textile Research，2013，34（11）：34-38（in Chinese）.

[6]TUNAK M，LINKA A.Analysis of planar anisotropy of fibre systems by using 2D Fourier transform[J].Fibres&Textiles in Eastern Europe，2007，15（5/6）：64-65.

[7]TUNAK M，ANTOCH J，KULA J，et al.Estimation of fiber system orientation for nonwoven and nanofibrous layers：Local approach based on image analysis[J].Textile Research Journal，2014，84（9）：989-1006.

[8]CHIKKERUR S，CARTWRIGHT A N，GOVINDARAJU V.Fingerprint enhancement using STFT analysis[J].Pattern Recognition，2007，40（1）：198-211.

[9]RATAJ J，SAXL I.Analysis of planar anisotropy by means of the Steiner compact[J].Journal of Applied Probability，1989，26（3）：490-502.

[10]RATAJ J，SAXL I.Analysis of planar anisotropy by means of the Steiner compact：A simple graphical method[J].Acta Stereologica，1988（7）：107-112.

[11]彭章平，彭小奇，伍更新.基于非平稳信号频谱分析的指纹图像增强算法[J].数据采集与处理，2008，23（1）：35-39.PENG Z P，PENG X Q，WU G X.Fingerprint enhancement algorithm based on non-stationary signal frequency spectrum analysis[J].Journal of Data Acquisition and Processing，2008，23（1）：35-39（in Chinese）.

[12]曾跃民，刘丽芳.基于计算机图像处理的非织造布质量检测与控制技术[J].非织造布，2001，9（3）：37-40.ZENG Y M，LIU L F.Nonwovens properties detection and control technology based on computer image processing[J].Textile College，2001，9（3）：37-40（in Chinese）.

[13]郭永平，徐增波.傅里叶变换技术在织物和无纺布结构参数测试中的应用[J].中国纺织大学学报，1998，24（6）：18-22.GUO Y P，XU Z B.Application of Fourier transform technique in the measurement of structural parameters in fabrics and nonwovens[J].Journal of China Textile University，1998，24（6）：18-22（in Chinese）.

[14]迟华山，王红星，郭奇，等.短时傅里叶变换在线性调频信号时频滤波中的应用[J].电讯技术，2012，52（2）：155-159.CHI H S，WANG H X，GUO Q，et al.Application of STFT in time-frequency filtering of LFM signals[J].Telecommunications Engineering，2012，52（2）：155-159（in Chinese）.

[15]CHIKKERUR S，CARTWRIGHT A N，GOVINDARAJU V.FingerprintenhancementusingSTFT analysis[J].Pattern Recognition，2007，40（1）：198-211.