波动预测建模与尾部风险测量方法

陈声利，李一军，关 涛

1 北京大学 光华管理学院，北京 100871 2 嘉实基金管理有限公司，北京 100005 3 哈尔滨工业大学 管理学院，哈尔滨 150001

引言

2015年股指期货经历了一轮激烈的牛熊市，许多投资者在异常波动中遭受损失。极端波动状态下资产收益率的尾部风险对投资者的决策行为产生影响，准确测量资产收益率的尾部风险，有助于投资者预判风险、规避损失以及管理组合，有助于监管部门跟踪和防范市场的系统性风险。在股指异常波动阴影下，研究股指期货尾部风险的测量方法，对风险管理[1-3]、资产配置[4-6]和市场监管具有理论意义和实践意义。

尾部风险研究的核心是建模预测未来资产收益率的风险边界。目前，在险价值(value at risk, VaR)和预期损失(excepted shortfall, ES)是测量尾部风险的主流方法。VaR模型的经济意义明确且计算简便，在理论和实务上应用广泛。由于VaR模型不满足次可加性，ARTZNER et al.[7]提出满足一致性风险测量的ES模型。资产波动率是VaR模型和ES模型估计的核心变量，准确估计和预测波动率是测量尾部风险的重要环节。

利用VaR模型和ES模型测量尾部风险时，极值理论(extreme value theory, EVT)在无需了解收益率分布下可对尾部行为进行概率估计，是常用且有效的参数化方法[7]。极值理论的传统用法是借助SV、GARCH等模型估计低频波动率。然而，高频数据催生了以已实现波动率为代表的高频波动率，它比低频波动率蕴含更多信息且计算效率更高。因此，将高频波动率用于测量尾部风险已成为研究趋势。

近年来，已实现波动率的研究出现了新进展，它既能分解为连续波动和跳跃波动，又能分解为好波动和坏波动，并进一步衍生出符号跳跃。如何将跳跃波动、好坏波动和符号跳跃等新型结构波动率用于测量尾部风险是建模难点。本研究在极值理论基础上引入跳跃波动、好坏波动和符号跳跃等新型高频波动率，构建RV-EVT尾部风险测量方法，以沪深300股指期货为实证研究对象，回测分析RV-EVT框架下波动预测模型的优劣，进一步探讨尾部风险的实践应用。

1相关研究评述

1.1VaR和ES测量方法

VaR和ES测量方法包含参数方法和无参化方法[8-9]，参数化方法包括指数加权法、等权重法、GARCH法和极值理论法等，无参化方法主要包括历史模拟法和蒙特卡洛模拟法等。

随着高频波动率的兴起，大量学者将已实现波动率用于尾部风险VaR和ES的估计。部分学者在估计VaR和ES的特定模型下比较不同波动率的优劣，BROWNLEES et al.[10]建立ARFIMA和HAR等模型预测尾部风险VaR，实证比较RV、RR、BV、TSRV和RK等高频波动率的优劣；王天一等[11]采用realized GARCH模型估计VaR后，瞿慧等[12]基于realized GARCH模型预测尾部风险VaR和ES，实证比较RV、RR、BV、MedRV、TSRV和RK的优劣。

还有部分学者根据收益率分布或波动率结构，建立新的尾部风险VaR和ES测量方法。王春峰等[13]基于下跌已实现半方差RS-捕捉波动率的杠杆效应，构建ARFIMA-GARCH模型预测RS-，利用偏t分布SKST-RS-模型预测VaR和ES；考虑跳跃和杠杆效应，柳会珍等[14]建立HAR和HARXRL-RV-J模型预测已实现波动率，利用EVT方法预测VaR；樊鹏英等[15]基于已实现波动率建立PGARCH模型预测VaR。

1.2VaR和ES极值理论方法

极值理论在收益率分布未知条件下，使用越槛高峰(peak over threshold，POT)模型拟合有限极端观察值的分布，被认为在实践中是有效的[1,8,16]。MCNEIL et al.[1]构建两步法的条件EVT模型(C-EVT)，先用AR-GARCH模型对资产收益率进行白噪声预处理，然后采用POT模型估计GARCH模型的标准残差尾部分布。MCNEIL et al.[1]和魏宇[16]通过实证分析证明C-EVT模型具有有效性。

在C-EVT模型基础上，BEE et al.[2]引入已实现波动率的预测建模，构建两步法RV-EVT尾部风险测量方法，先用HAR-RV类模型对收益率进行白噪声，然后用EVT模型拟合残差尾部。该方法的关键工作是引入3类连接函数，建立HAR类模型的预测值与条件收益波动率的转换关系，对未来1天和10天的VaR和ES的回测分析结果表明，RV-EVT模型的尾部风险测量水平比GARCH族低频波动率建立的C-EVT模型更佳。

1.3波动预测建模方法

波动率估计和建模是测量风险的重要环节。考虑低频波动率的VaR和ES风险测量时，一般需假定收益率分布，并运用SV、GARCH、FIGARCH、APARCH类模型估计和预测条件收益波动率[10]。这些方法参数估计繁琐，无法利用高频数据信息。因此，高频波动率的风险测量应用成为趋势。

波动率预测(简称为波动预测)建模领域，HAR模型框架能较好地刻画波动长记忆性。CORSI[17]将交易者分成日线、周线和月线交易者，首次提出采用HAR-RV模型预测已实现波动率。考虑跳跃波动，CORSI et al.[18]和ANDERSEN et al.[19]提出HAR-RV-J和HAR-RV-CJ模型。考虑已实现半方差和符号跳跃[20]，PATTON et al.[21]和 AUDRINO et al.[22]构建HAR-RV-RS和HAR-RV-SJ等模型，探讨好坏波动和符号跳跃的不对称波动预测能力。考虑跳跃波动率、好坏波动和符号跳跃等新型波动率，诸多研究已将HAR类模型用于测量尾部风险，并证实其风险测量能力比GARCH类模型表现更优[2,14,23]。

1.4相关的实证研究

风险测量模型VaR和ES的优劣比较是实证研究的热点。杨娴等[8]研究表明当金属期货大涨或大跌时，ES比VaR能更准确地测量市场风险；王春峰等[13]利用中国股市数据的实证分析表明，在VaR测量极端风险失效时，ES能够较好地对尾部风险进行管理；杨坤等[24]结合极值理论构建5类copula模型测量原油尾部风险，并证实VaR在低风险时测量尾部较好，ES在高风险时测量尾部更优异。此外，秦学志等[25]以股指期货为研究对象，证实极值理论对测量尾部风险VaR和ES的有效性，并通过设定不同风险厌恶满足不同风险偏好的风控需求。因此，VaR模型和ES模型对不同资产标的的风险测量存在性能差异。

在尾部风险的实证研究中，学者们挖掘了尾部风险的资产定价能力。针对国外市场，ALLES et al.[26]利用高阶矩建模，研究亚洲市场的下尾风险的风险补偿；BOLLERSLEV et al.[27]研究尾部风险溢价，结果表明跳跃尾部可预测收益率。针对中国市场，陈国进等[28]利用极值理论提取中国个股横截面的尾部风险，并证实尾部风险对股市横截面收益率具有解释能力；邢红卫等[29]利用Fama-French因子模型挖掘尾部风险对A股的定价能力。另外，尾部风险研究可用于投资组合管理。MOREIRA et al.[5]采用已实现波动率估计VaR，进而将其用于投资组合的建模研究；VIKAS et al.[30]针对对冲基金构建尾部风险测量方法，研究尾部风险的来源识别以及尾部风险对投资组合的冲击。由此可知，尾部风险研究对资产定价和投资组合具有理论和实践价值。

1.5已有研究不足和研究目的

已有研究的不足：①异常波动情形下投资者和监管者迫切需要跟踪尾部风险的有效方法，但针对股指期货的风险测量方法研究较少；②中国鲜有研究在极值理论框架下探讨高频波动率的风险测量应用，特别是跳跃波动和好坏波动等新型波动率的研究；③BEE et al.[2]提出RV-EVT尾部风险测量框架，但未详实探讨不同HAR波动预测模型、不同测量模型VaR和ES的尾部风险测量水平差异；④鲜有研究探讨尾部风险测量在量化交易中的应用。

针对现有不足，本研究的主要目的：①以股指期货为研究对象，利用高频波动率和极值理论构建有效的RV-EVT尾部风险测量方法；②将已实现波动率衍生出的跳跃波动、好坏波动和符号跳跃引入HAR波动预测建模，以经典的HAR-RV模型为比较基准，通过滚动预测分析HAR类波动模型优劣，并在RV-EVT框架下比较它们的风险测量水平差异；③通过日线和周线尾部风险的回测分析，比较分析VaR和ES模型对股指期货尾部风险测量的差异；④基于RV-EVT尾部风险方法建立可执行的资金管理模型，并通过量化交易策略回测探讨其有效性。

2波动预测建模方法

2.1二次变差理论

P为资产对数价格，假设P=(Pt)t>0定义在概率空间(Ω,F,(Ft)t>0,P)和适应于过滤项(Ft)t>0的对数价格过程，Pt为对数价格过程，Ω为概率空间，F为过滤项，(Ft)t>0表示对过滤项在时间上取正值。在给定的过滤概率空间下，资产对数价格服从半鞅过程，即

dPt=υ(t)dt+σ(t)dW(t)+κ(t)dο(t)

(1)

其中，t为时间，υ(t)为连续有界的漂移函数，σ(t)为左极限、右连续的随机波动过程，W(t)为标准布朗运动，κ(t)为跳跃大小，ο(t)为计数过程。

根据二次变差理论，由(1)式得到第t天的对数收益率的二次变差过程，即

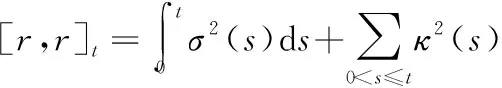
(2)

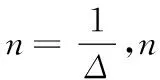
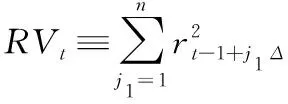
(3)

其中，RV为已实现波动率，rt-1+j1Δ为日内高频收益率，j1为日内高频收益率的序号。借鉴ANDERSEN et al.[19]的极限定理进行推导，当采样间隔Δ→0时，在(2)式和(3)式的基础上得到

RVt→IVt+JVt

(4)

进一步，由(4)式得到跳跃方差的一般化估计。采用已实现双幂差[33-34]估计连续波动后，跳跃方差可表示为

JVt=RVt-BVt

(5)

其中，BV为已实现双幂差。

然而，(5)式包含大量非零小跳跃[35]。为消除不显著的小跳跃，需构建统计量检验跳跃方差，即

Jt=I[·]·(RVt-BVt)

(6)

其中，Jt为显著的跳跃方差；I[·]为示性函数，统计量显著时取值为1，否则取值为0。

2.2连续波动和跳跃波动

无参化跳跃检测是甄别显著跳跃的主流方法。开创性的工作是由BARNDORFF-NIELSEN et al.[33-34]构建的BNS跳跃检测框架。然而，在市场微观结构噪声影响下，RV和BV是有偏估计。于是，在BNS框架下学者们[36-38]通过噪声纠偏构建误差更小的波动率估计量，从而得到更稳健的跳跃检验法。代表性的成果包括ANDERSEN et al.[19]的ABD检验法、CORSI et al.[18]的CPR检验法、ANDERSEN et al.[39]的ADS检验法，CPR检验法和ADS检验法较为常用。本研究采用性能较优的CPR检验法，杨科等[40]和马峰等[41]已就中国市场验证了其有效性。

本研究采用HANSEN et al.[42]提出的已实现核估计对CPR检验法的RV进行噪声偏差校正，即

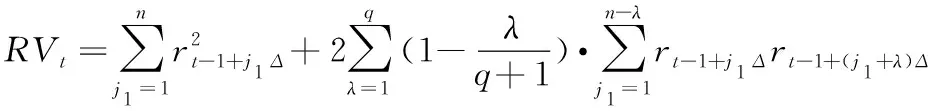
(7)

其中，rt-1+j1Δ和rt-1+(j1+λ)Δ为两个相邻的日内高频收益率，q为较小的非负整数，λ为不大于q的非负整数。选取q=λ=1，则已实现波动率修正为

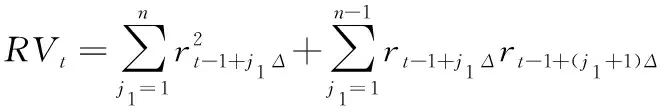
(8)

为减少已实现双幂差易受噪声的影响，借鉴CORSI et al.[18]提出的修正门限已实现多次幂差，即

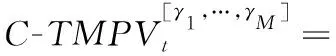
(9)

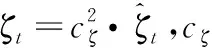
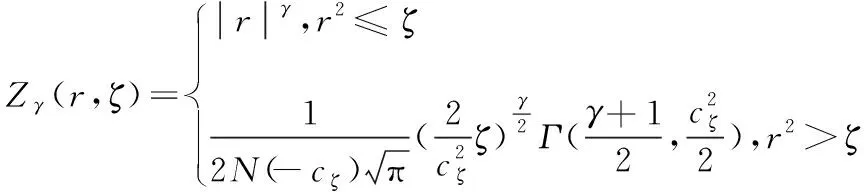
(10)

其中，N(·)为标准正态分布函数。因此，门限函数的作用是当高频收益率出现异常时，高频收益率的指数幂采用随机门限函数进行估计。在此基础上，修正门限双幂次波动率和修正门限四次幂差波动率表示为

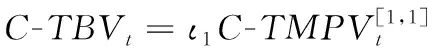
(11)

(12)

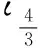
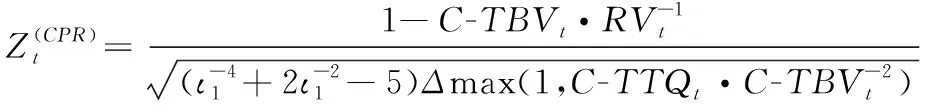
(13)

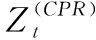
(14)

(15)

其中，Jt,α为显著跳跃，Ct,α为连续波动，α为置信水平，Φα为临界值。

2.3好坏波动和符号跳跃

在已实现波动率基础上，借鉴BARNDORFF-NIELSEN et al.[20]的研究，根据正负收益率平方和定义上涨已实现半方差和下跌已实现半方差，即

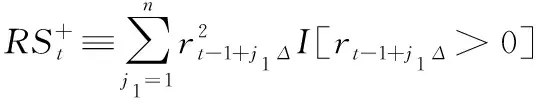
(16)

(17)

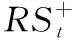
本研究延续陈声利等[43]的研究，利用已实现核估计修正好坏波动，得到

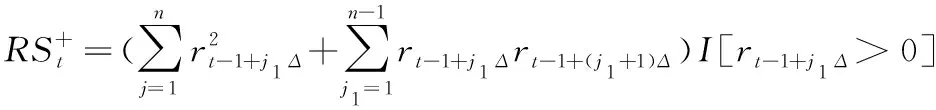
(18)

(19)

借鉴PATTON et al.[21]的研究，依据上涨已实现半方差和下跌已实现半方差定义符号跳跃，即

(20)

其中，SJ为符号跳跃，符号跳跃刻画了波动不对称性和波动方向，由它衍生的正负符号跳跃表示为

(21)

(22)

2.4HAR波动预测建模

波动预测建模领域，CORSI[17]利用日线、周线和月线波动，提出HAR-RV模型预测已实现波动率。沿用异质波动建模框架，ANDERSEN et al.[19]、PATTON et al.[21]和AUDRINO et al.[22]考虑跳跃波动、好坏波动和符号跳跃，先后提出HAR-RV、HAR-RV-CJ、HAR-RV-RS和HAR-RV-SJ模型。马峰等[41]研究证明对数形式的HAR模型具有更高的预测精度。

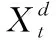
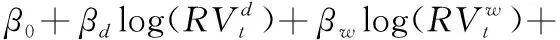
(23)

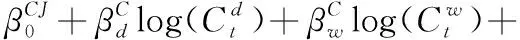
(24)

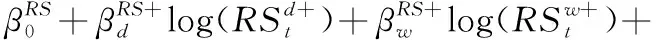
(25)

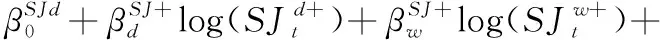
(26)

其中，h为多期预测变量，β0系列为截距项，β系列为回归系数，ε系列为残差项。

需要指出的是，BEE et al.[2]的RV-EVT风险测量框架仅考虑日线跳跃和符号跳跃的波动冲击。本研究对该理论框架进行补充，增加日线、周线和月线的异质波动冲击建模。

3RV-EVT风险测量方法

3.1极值理论的分布

资产收益率可表示为均值方差过程，即

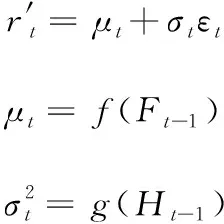
(27)

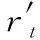
假定分布函数F存在上边界vF，vF:sup{t:F(t)<1}，给定最大阈值u(u0，v>0。那么，当u→vF，Pr(t-u≤x|t>u)趋近于

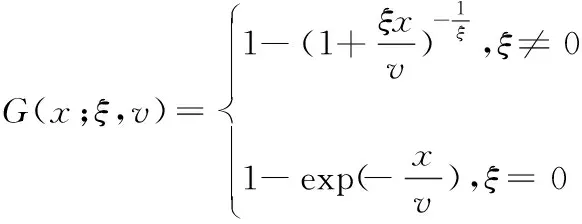
(28)

其中，x为超出量序列的上界。

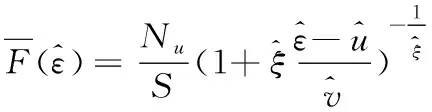
(29)

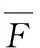
3.2尾部风险的估计

(1)VaR的计算

给定置信水平α下第t天在险价值估计量为

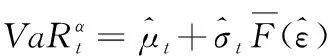
(30)

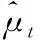
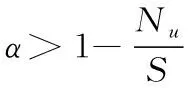
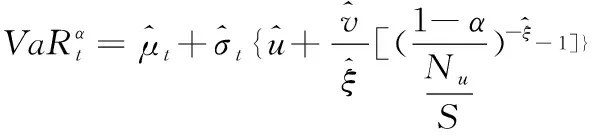
(31)

(2)ES的计算

预期损失ES也被称为条件风险价值，它测量的是超过VaR水平的条件期望值。以下尾风险为例，ES估计量为

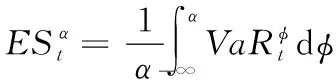
(32)

其中，φ为积分变量。

根据(31)式和(32)式可推导出预期损失的估计量，即

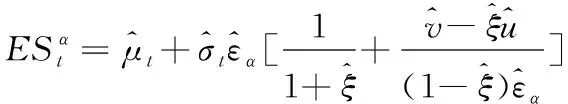
(33)

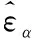
3.3波动预测的连接函数

RV-EVT建模框架的出发点是在(27)式中的信息集Ft-1和Ht-1中嵌入日内高频信息，并使用极值模型拟合残差尾部参数。两步法RV-EVT框架是先通过HAR类模型代替GARCH类模型对收益率进行白噪声处理，然后再利用POT模型估计其尾部参数。对已实现波动率的预测和建模，能够提升波动率的预测精度，进而更准确地估计尾部风险。

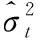
类型1CLEMENTS et al.[45]提出的简单连接函数，即

(34)

类型2BROWNLEES et al.[46]提出的连接函数，即

(35)

其中，a和b为调整系数。

类型3BEE et al.[2]考虑残差修正提出的连接函数，即

(36)

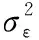
BEE et al.[2]实证对比上述3类连接函数，最终发现简单连接函数表现最佳。因此，本研究实证分析时选用(34)式。

考虑已实现波动率的多期预测，借鉴BEE et al.[2]的研究，将VaR和ES的估计量定义为

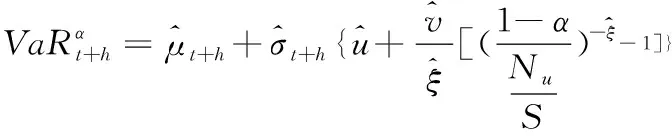
(37)

(38)

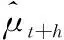
3.4回测分析方法

回测分析通过比较风险测量模型的估计结果与理论预期的差异来评估模型优劣。若风险测量模型的估计结果与理论预期相近，则说明该模型的准确性较高；若二者偏差较大，则预示该模型的准确性较低。目前，风险测量模型评估方法虽然较多，但VaR和ES回测分析最常用评估方法分别是KUPIEC[47]提出的无条件覆盖检验和MCNEIL et al.[1]提出的自枚举检验。王鹏等[44]和杨坤等[24]的研究说明上述检验方法具有有效性。

(1)无条件覆盖

KUPIEC[47]提出无条件覆盖检验的初衷是检测VaR模型的预测失败率是否趋于期望失败率。本研究以多头头寸的下尾风险为例(空头时概率水平为(1-α))，阐述无条件覆盖检验的主要步骤。

步骤1在置信水平为α的概率水平下，定义第t天的碰撞序列为

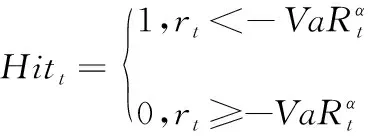
(39)

其中，Hit为碰撞序列。

步骤2在置信水平为α的概率水平下，若VaR测量模型足够准确，则碰撞序列应服从置信水平为α的概率值的Bernoulli分布，即

Hitt～Ber(α)

(40)

令T为碰撞序列总天数，N为超出下尾风险的序列总天数，原假设和备择假设定义为

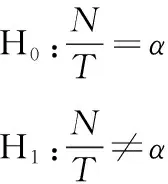
(41)

由此可见，原假设可归结为经验频率是否足够趋近于理论概率。

步骤3根据Bernoulli分布性质，似然函数表示为

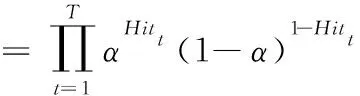
=αN(1-α)T-N

(42)

其中，L(α)为似然函数。

本研究采用KUPIEC[47]构建的似然比函数作为检验统计量，即

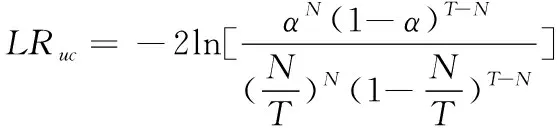
(43)

其中，LRuc为似然比函数。

步骤4当原假设正确时，KUPIEC[47]证明似然比函数服从自由度为1的χ2分布，即

LRuc→χ2(1)

(44)

因此，在置信水平α下，如果计算的LRuc超出χ2(1)的临界值(即落入拒绝域)，则拒绝原假设；反之，则接受原假设，即认为VaR的风险测量模型足够准确。

实际运用中，判断拒绝或接受原假设的定量标准是无条件覆盖检验的p值是否具有显著性[47]。如果某个风险测量模型计算的VaR的无条件覆盖检验的p值越大，说明越不能拒绝原假设，表明该风险测量模型估计VaR的准确性越高[44,47]。

(2)自枚举检验

MCNEIL et al.[1]提出针对ES回测分析的自枚举检验(bootstrap)。自枚举检验的主要思想是构建多个bootstrap残差样本，并利用其计算检验统计量和p值。借鉴MCNEIL et al.[1]和王鹏等[44]的研究，本研究的主要步骤概括如下。

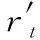
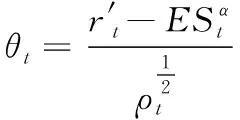
(45)

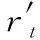
步骤2假定z为超出残差样本数量，lt为初始残差序列，则初始残差序列定义为

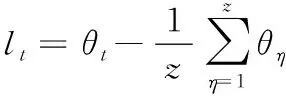
(46)

(47)

步骤4为了得到统计量δ(l)的分布及其p值，需生成范围在{1,2,…,m}的m个均匀分布随机数，并以该随机数对应的残差序列lt构建新样本。重复S次(本研究取S=1 000)，得到S个新的bootstrap样本。

步骤5针对每个bootstrap样本i，i=1,2,…,S，利用(47)式算出检验统计量δi(l)，分别记为{δ1(l),δ2(l),…,δS(l)}。特别的，初始样本的δ(l)可记为δ0(l)。因此，可求得检验统计量δ(l)的经验分布。

步骤6由于超出残差θt通常表现为右偏分布，因此bootstrap检验的备择假设为E(θ)>0，相应的原假设为E(θ)=0。根据MCNEIL et al.[1]的推导，计算统计量{δ1(l),δ2(l),…,δS(l)}大于δ0(l)的样本比例，即为显著检验的p值。p值越大，越不能拒绝原假设，预示波动模型对ES测量的准确性越高。

4实证分析

4.1数据说明和波动分解

本研究数据源自程序化交易平台MultiCharts 8.8，均从中国金融期货交易所撮合成交的股指期货合约数据进行实时接收和汇总。本研究选取股指期货主力连续数据为研究对象，主力连续数据是由相邻的股指期货主力合约成交数据汇总，它在主力合约换月之前将成交量更大的下月合约作为主力连续数据。因此，主力连续数据具有充足的流动性。

本研究同时获取沪深300股指期货主力连续日度数据和每天的5分钟高频数据。日度数据的时间区间为2011年1月1日至2017年1月1日，计1 457个交易日。在2016年1月1日股指期货交易时间与A股的开收盘同步之前，每天的5分钟高频数据为54个，之后为每天48个。本研究获取的5分钟高频数据是固定间隔数据，无需进行额外清洗。本研究滚动预测未来日线和周线的VaR和ES，将滚动时间窗固定为765天，样本外预测集为488天(2014年4月5日至2016年4月5日)。预测样本覆盖了窄幅波动的低迷市和异常波动的牛熊市。本研究综合使用Python、MultiCharts、Traderblazer程序化交易语言进行实证分析。

为了提高计算精度，本研究将收益率放大100倍。为增进读者对原始数据和收益率的认识，图1给出股指期货每日收盘价序列和对数收益率序列，表1给出股指期货收益率的描述性统计结果。由表1可知，①从JB统计量可知，股指期货收益率不服从正态分布，且收益率呈现尖峰厚尾(峰度大于3)和有偏形态(2012年和2014年为右偏，其余年份为左偏)；②Ljung-Box Q的检验结果表明，在5%水平上股指期货收益率序列的长记忆性不够显著；③ADF单位根检验的结果表明，股指期货收益率序列是平稳的；④2015年的标准差出现异常值，反映了当年异常波动行情。

高频波动的估计需先选定抽样频率。由于国内外学者一般采用5分钟高频数据作为抽样频率[2,18,21]，本研究也选取5分钟高频数据估计高频波动率。利用CPR检验法识别跳跃时，将置信水平设定为α=0.990。在此基础上，根据高频收益率序列可计算出股指期货已实现波动率及其衍生波动率序列。根据(14)式和(15)式已实现波动率可分解为连续波动和跳跃波动，根据(18)式和(19)式已实现波动率可分解为好波动和坏波动，根据(20)式和(21)式好坏波动又衍生出正向符号跳跃和负向符号跳跃。在本研究中依次计算上述变量，时间跨度从2011年1月1日至2017年1月1日。在跳跃检测时，由换合约所致的隔夜跳跃已被剔除。由于本研究侧重于尾部风险预测，主要依据样本外滚动预测结果，因此上述新型结构波动率的特征、性质及波动冲击行为在此不予详述。

4.2已实现波动率的滚动预测

估计尾部风险VaR和ES需先预测未来波动率，下面分析已实现波动率的滚动预测结果。针对HAR类模型的样本内和样本外预测分析，陈声利等[43,48]揭示了波动冲击行为与预测模型的优劣，本研究与之不同之处在于采用对数形式的HAR建模，并讨论样本外滚动预测模型的优劣。

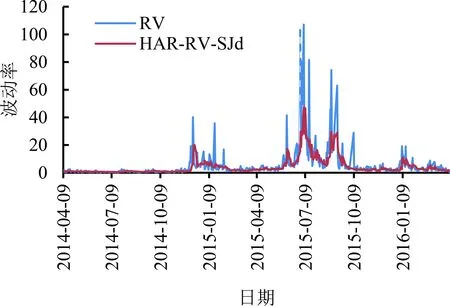
本研究利用Python实现HAR-RV、HAR-RV-CJ、HAR-RV-RS和HAR-RV-SJd4个模型(见(23)式～(26)式)的日线已实现波动率滚动预测结果，见图2。由图2可知，4个模型的滚动预测效果较好，体现了对数形式波动预测建模的有效性。对于样本外滚动预测时评估模型的损失函数，本研究采用均方误差MSE和平均绝对误差MAE，其数学定义为

(48)

(49)

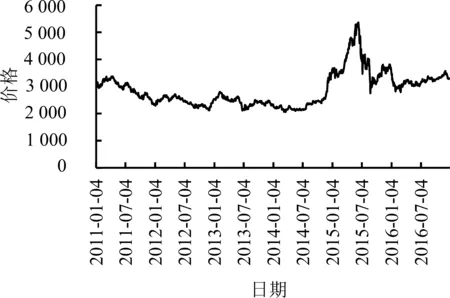
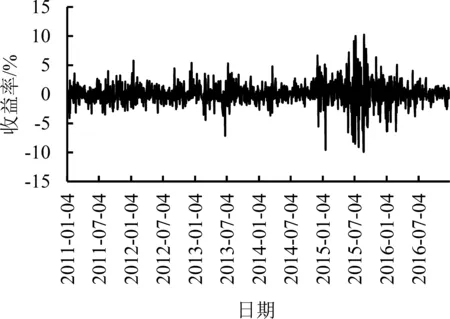
(a)收盘价序列(b)收益率序列

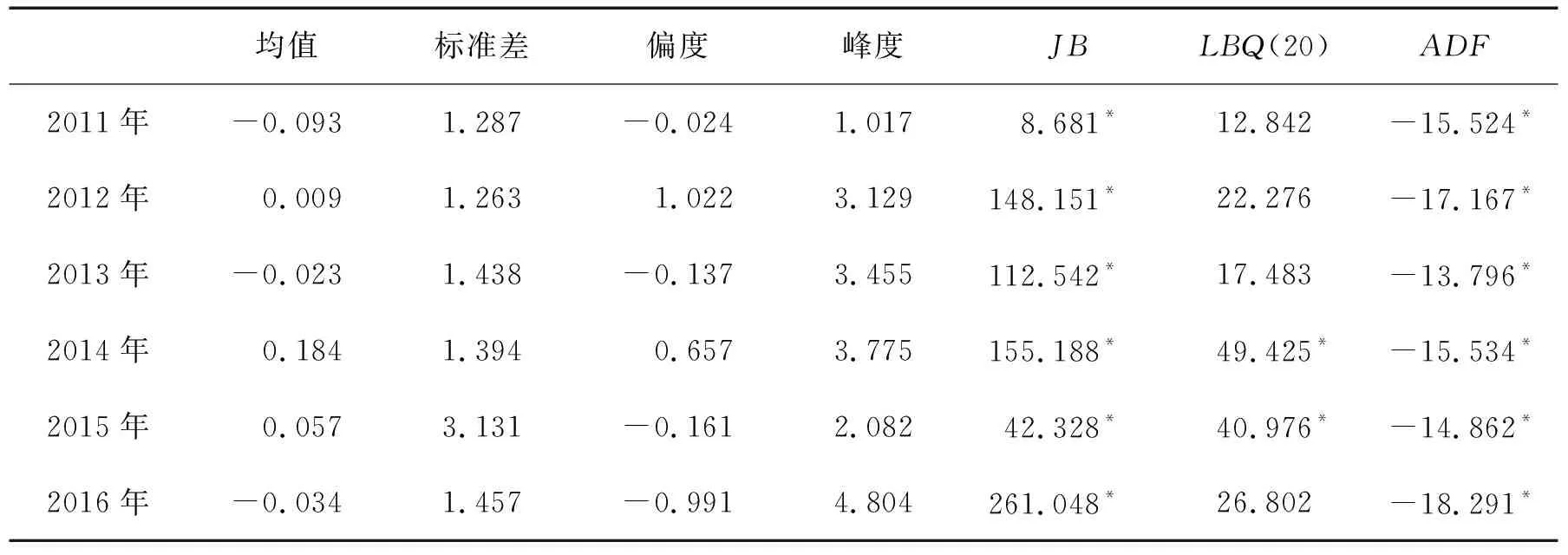
均值标准差偏度峰度JBLBQ(20)ADF2011年-0.0931.287-0.0241.0178.681*12.842-15.524*2012年0.0091.2631.0223.129148.151*22.276-17.167*2013年-0.0231.438-0.1373.455112.542*17.483-13.796*2014年0.1841.3940.6573.775155.188*49.425*-15.534*2015年0.0573.131-0.1612.08242.328*40.976*-14.862*2016年-0.0341.457-0.9914.804261.048*26.802-18.291*

注：JB为Jarque-Bera检验统计量，LBQ(20)为滞后20阶的Ljung-Box Q检验，ADF为单位根检验，*为在5%水平上显著。

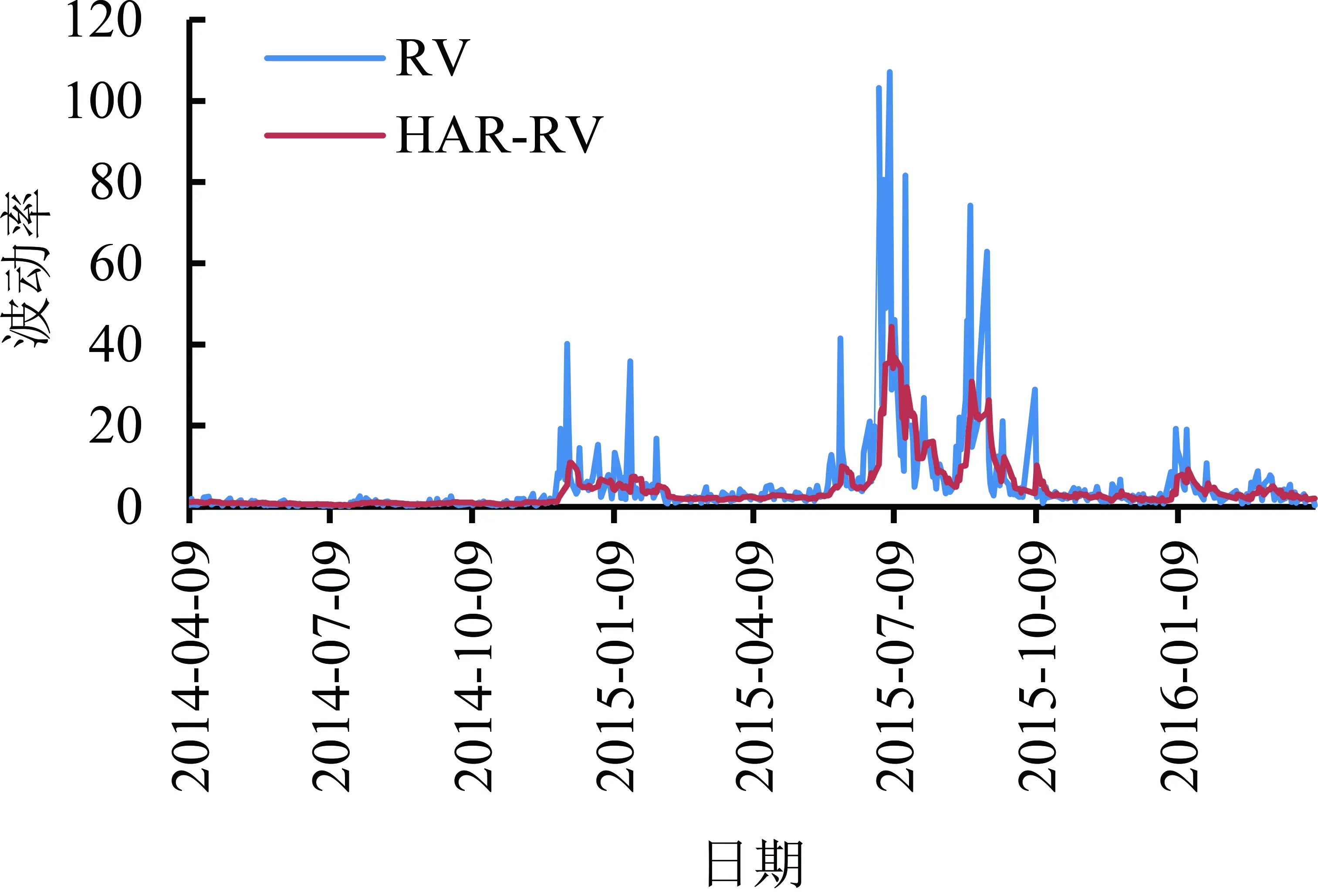
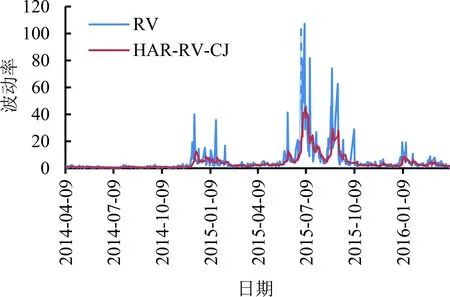
(a)HAR-RV(b)HAR-RV-CJ

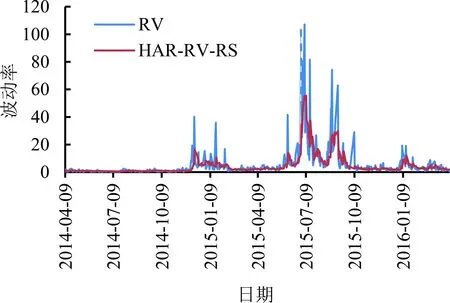
(c)HAR-RV-RS(d)HAR-RV-SJd

其中，Nroll为滚动预测的目标数。表2和表3给出股指期货日线和周线已实现波动率的滚动预测结果，表中的黑体数据为预测模型的损失函数值最小。

由表2可知，针对日线已实现波动率的预测，4个模型的MSE和MAE大致呈现依次减小趋势，考虑好坏波动的HAR-RV-RS模型、考虑正负符号跳跃的HAR-RV-SJd模型的损失函数最小，它们的样本外滚动预测表现最佳。针对周线已实现波动率的预测，表3也呈现大致相同结论，而且两个损失函数都表明HAR-RV-SJd为最佳模型。此外，表2和表3中的样本内损失是在滚动时间窗上HAR类模型的拟合平均误差。上述4个HAR类模型的两种损失函数呈现出严格递减的趋势，该结果与样本外损失基本保持一致，也证实了上述模型的预测能力逐渐提升。鉴于此，滚动预测表现充分表明，HAR预测框架下已实现波动率分解能提高预测精度，好坏波动分解优于连续跳跃波动分解，好坏波动衍生出的符号跳跃具有极为突出的波动预测能力。

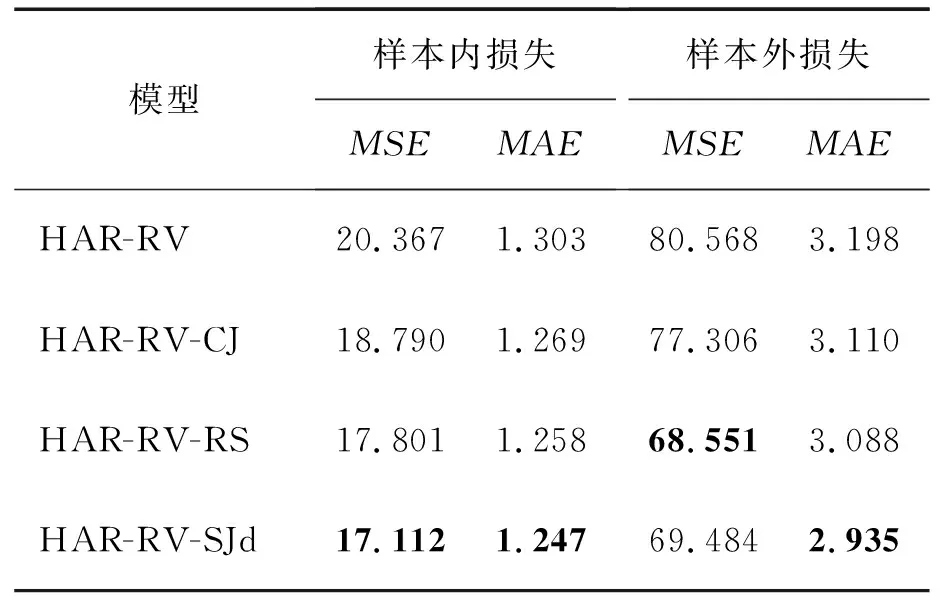
表2沪深300股指期货日线已实现波动率的滚动预测损失Table 2Rolling Forecasting Losses of Daily Realized Volatility for CSI 300 Index Futures

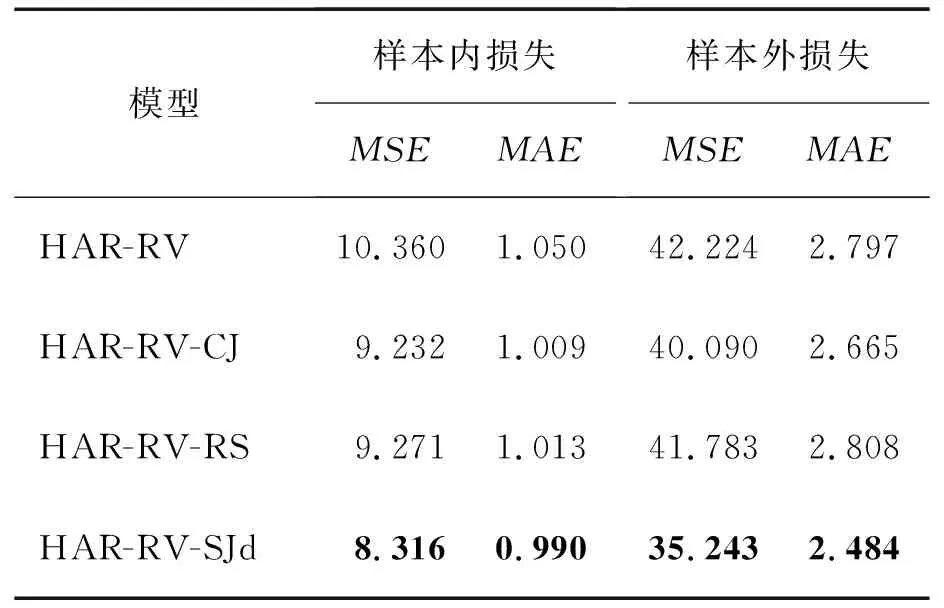
表3沪深300股指期货周线已实现波动率的滚动预测损失Table 3Rolling Forecasting Losses of Weekly Realized Volatility for CSI 300 Index Futures

4.3POT模型参数估计

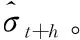
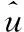
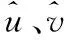
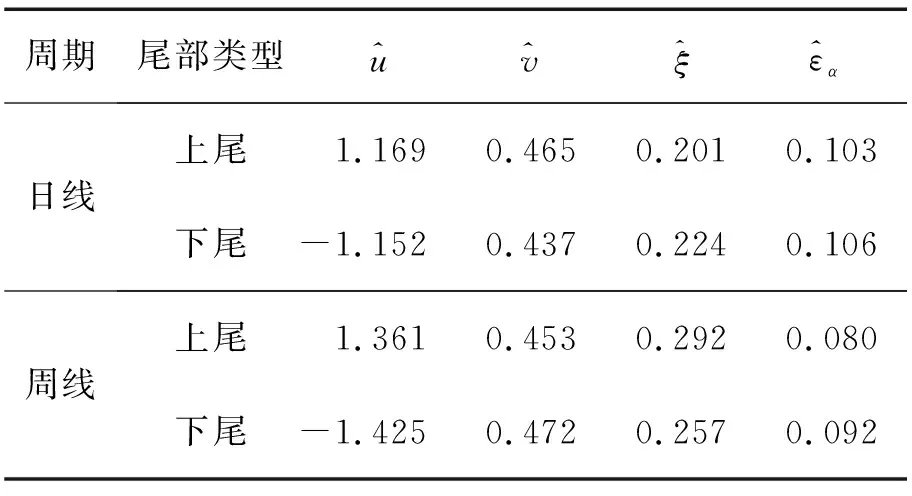
表4POT模型的参数估计结果Table 4Results for Parameter Estimations of POT Model

4.4VaR和ES的回测分析

采用KUPIEC[47]提出的无条件覆盖检验和MCNEIL et al.[1]提出的自枚举检验分别对VaR和ES的预测结果进行检验。经过上节一系列的参数估计，未来日线和周线的VaR和ES预测结果见表5和表6。

回测分析是在HAR类模型样本外滚动预测基础上展开的。检验样本数设定为滚动预测的目标数，即488天。选取0.900和0.950两个置信水平，则收益率超出尾部风险的预期值(简称为“理论超出数”)大致为50和25。表5和表6给出特定置信水平下不同HAR类波动预测模型的无条件覆盖检验和自枚举检验结果。表中上尾超出数为正向收益率高于上尾风险临界值的次数，下尾超出数为负向收益率低于下尾风险临界值的次数。回顾3.4节可知，回测分析检验的p值越大，越不能拒绝风险测量模型的原假设，意味着风险测量水平越准确。

分析表5未来日线的股指期货尾部风险预测结果，以下尾风险对测量结果进行解释，上尾风险测量情况类似。①针对股指期货尾部风险VaR和ES回测分析检验的多数模型的p值是显著的，即接受回测分析检验的原假设，说明RV-EVT尾部风险测量模型具有较好的短期风险测度能力；②在两种置信水平下，VaR和ES的超出数均大于理论超出数，说明RV-EVT模型测量的下尾风险边界比理论区间稍窄，意味着RV-EVT模型对股指期货极端风险控制得较为严格；③与VaR超出数相比，相同HAR类模型对应ES超出数更接近理论值，说明RV-EVT理论框架下ES模型比VaR模型对股指期货短期尾部风险的测量更优；④比较4类HAR模型发现，部分HAR-RV、HAR-RV-CJ模型p值未通过回测分析检验，且HAR-RV-RS和HAR-RV-SJd模型的超出数更接近理论值，说明考虑好坏波动和符号跳跃建模的RV-EVT风险测量模型更加出色。

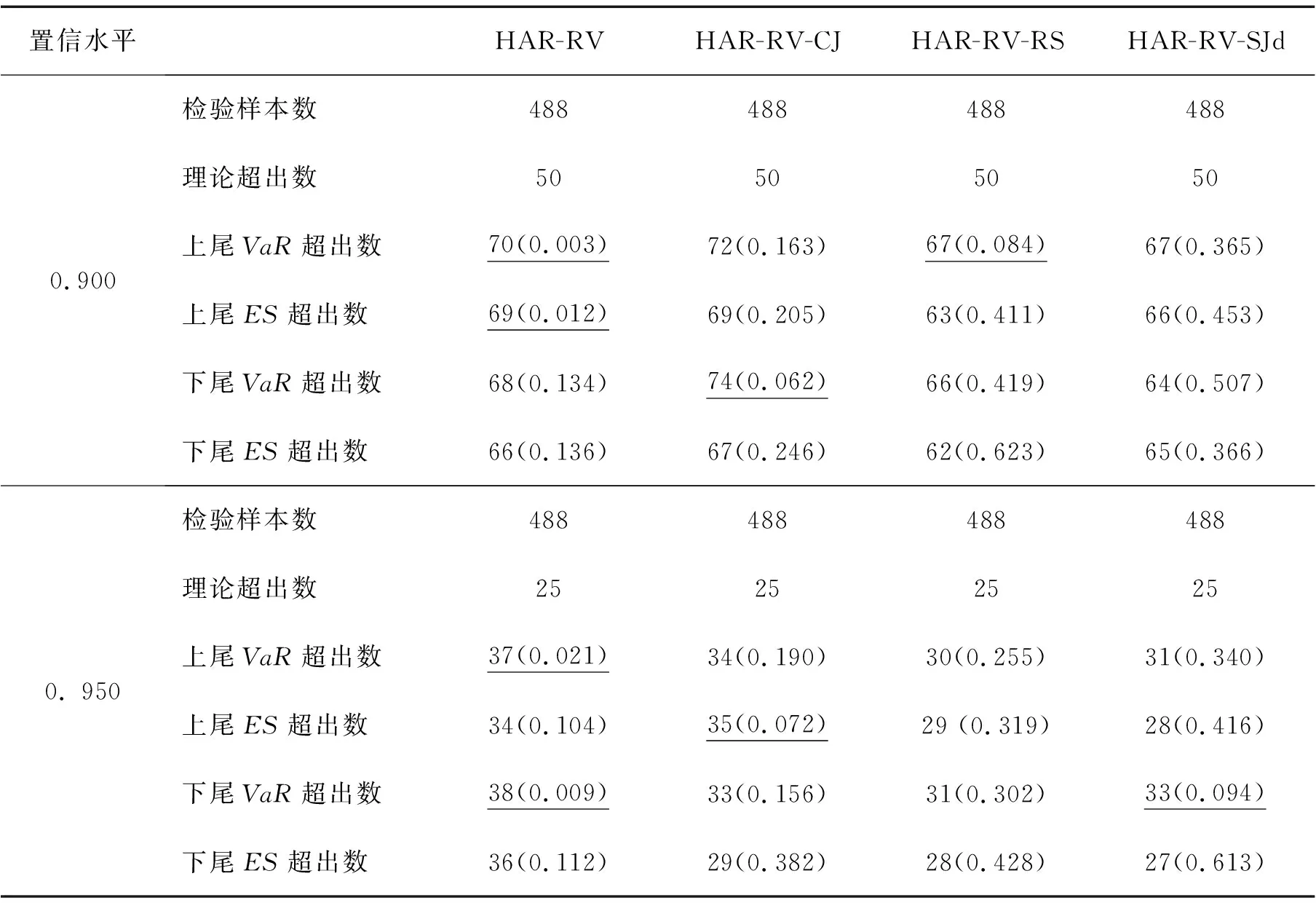
表5沪深300股指期货日线VaR和ES的回测分析结果Table 5Backtesting Analysis Results of Daily VaR and ES for CSI 300 Index Futures

注：与VaR超出数对应的括号内数据为无条件覆盖检验p值，与ES超出数对应的括号内数据为自枚举检验p值，p值越大，预示风险测量模型越准确。带有下划线的数据表示对应的模型为没有通过回测分析检验的模型。下同。

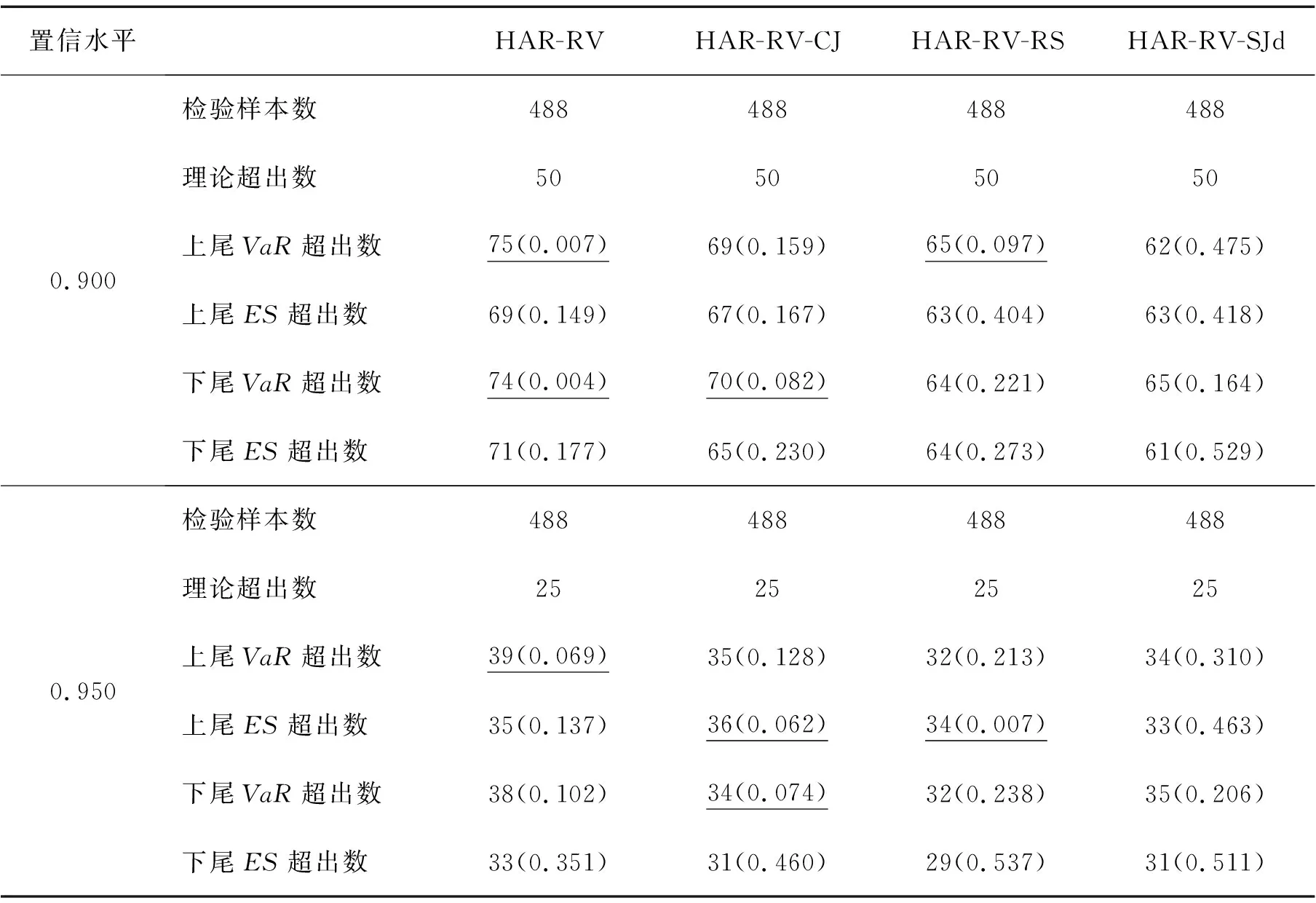
表6沪深300股指期货周线VaR和ES的回测分析结果Table 6Backtesting Analysis Results of Weekly VaR and ES for CSI 300 Index Futures

表6为未来周线的股指期货尾部风险预测结果。由于采用滚动预测方式，尾部风险周线预测的检验样本数和理论超出数与尾部风险日线预测时保持相同。①股指期货尾部风险VaR和ES回测检验的p值大多显著，即接受原假设，说明RV-EVT框架下的VaR和ES模型具有较好的周线风险测量能力；②在两种置信水平下，VaR和ES实际超出数均大于其理论超出数，这与BEE et al.[2]的实证结果一致；③ES普遍比VaR更接近理论超出数，体现出RV-EVT框架下的ES模型比VaR模型具有更好的长期尾部风险测量能力；④HAR-RV-RS和HAR-RV-SJd模型比其他模型的显著性更明显、超出数更接近理论值，也体现了好坏波动和符号跳跃在尾部风险测量中的价值。

根据上述分析可知，日线和周线的尾部风险测量水平证实了RV-EVT框架的有效性，且VaR和ES具有较优的测量水平。另外，在RV-EVT风险测量框架下，HAR-RV-RS和HAR-RV-SJd模型得到较优的VaR和ES测量水平。回顾4.2节的滚动预测分析，好坏波动或符号跳跃有效提高了波动率预测精度，而表5和表6的实证结果佐证了波动率预测精度提升能够提高尾部风险VaR和ES测量的准确性。因此，本研究在波动率预测建模中构建4类HAR模型，补充了BEE et al.[2]建立的HAR类模型，并验证了RV-EVT理论框架下应用HAR类模型在中国股指期货尾部风险测量的可行性。

为了更直观地观察VaR和ES对股指期货尾部风险的测量结果及其差异，图3给出股指期货下尾风险的10%VaR回测分析结果，图4给出股指期货下尾风险的10%ES回测分析结果。图3和图4的纵坐标为股指期货放大100倍的日度收益率，横坐标依次为时间从2014年4月5日至2016年4月5日累计488天的序号。由图3和图4可知，研究样本的前一年收益率波动较小，后一年收益率波动较大。为了比较VaR和ES在不同波动状态下的差异，本研究将2014年4月5日至2015年4月5日定义为样本1，将2015年4月6日至2016年4月5日定义为样本2，并统计VaR和ES模型在两个样本的收益率超出量占比，结果发现ES模型的超出量在样本1中比VaR模型少，但在样本2中比VaR模型多。

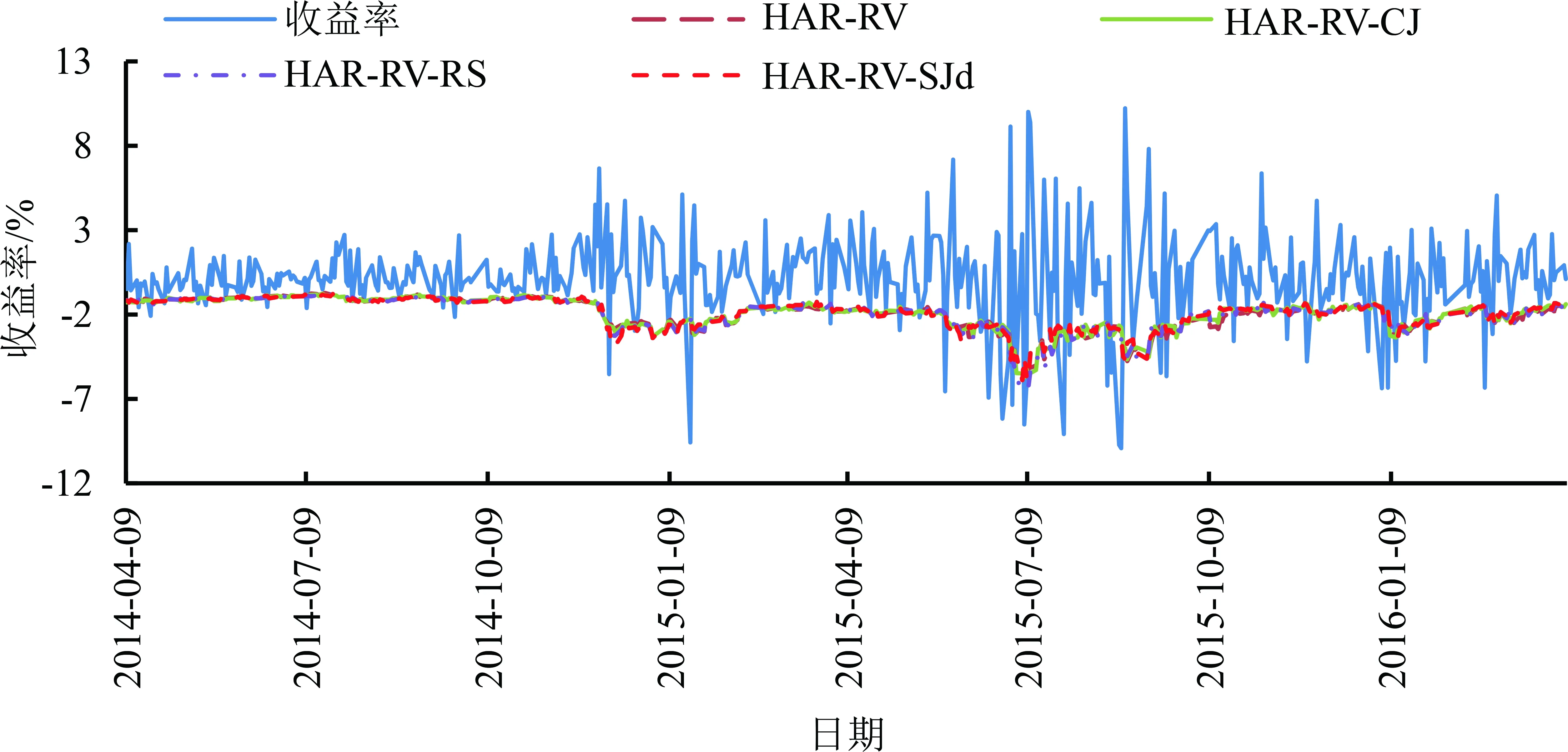
图3沪深300股指期货日线下尾风险的10%VaR回测分析结果Figure 3Backtesting Analysis Results of 10% VaR for Daily Downside Risk of CSI 300 Index Futures

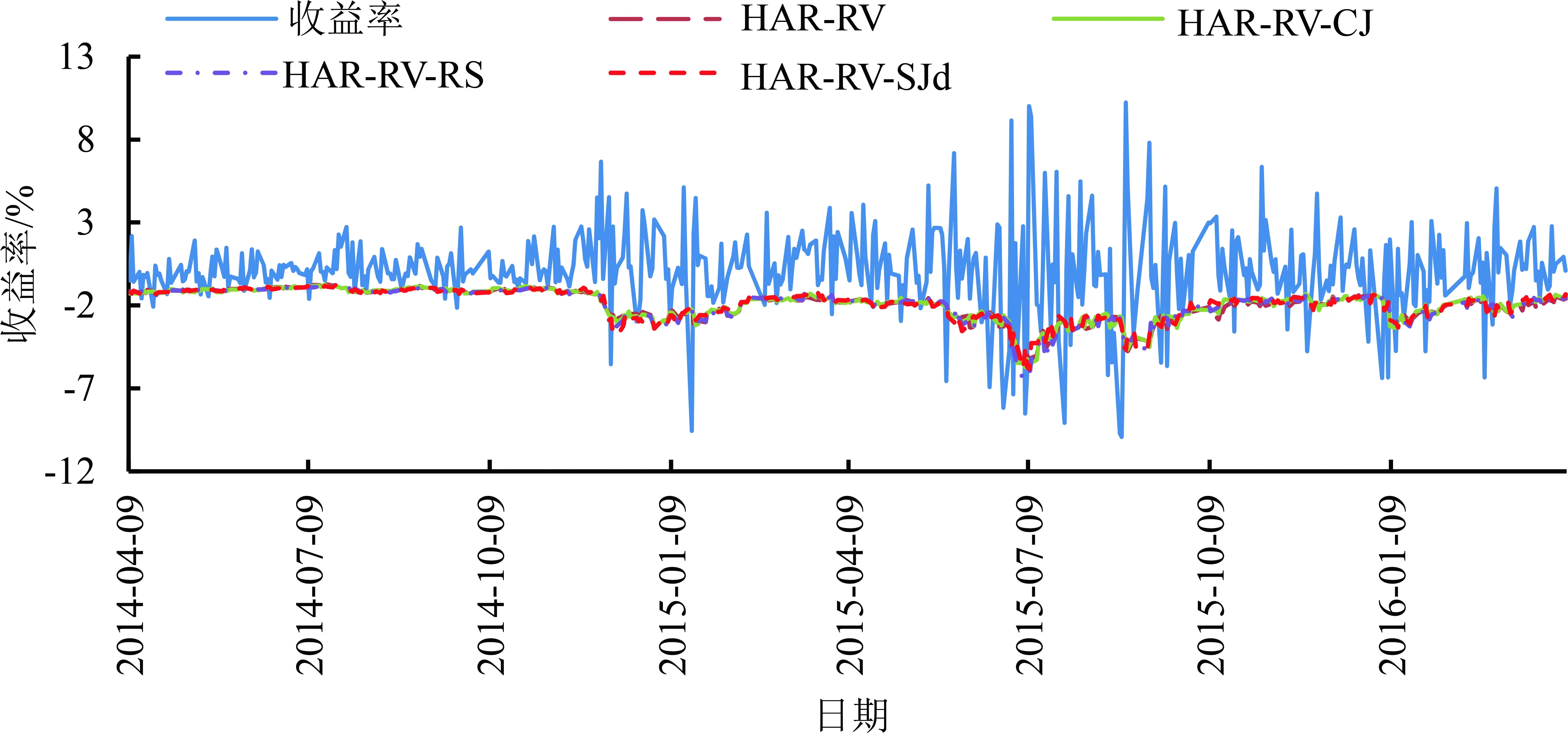
图4沪深300股指期货日线下尾风险的10%ES回测分析结果Figure 4Backtesting Analysis Results of 10% ES for Daily Downside Risk of CSI 300 Index Futures

综合上述分析可知，①收益率超出下尾风险VaR和ES预测值的数量与表5的结果大致吻合，说明本研究实证结果具有一定的可靠性。②在收益率波动较小的区域，根据不同HAR模型计算的VaR(或ES)较为接近；在收益率波动较大的区域，不同HAR模型计算的VaR(或ES)存在较大偏差。③在收益率波动较小区域，ES模型的超出数比VaR超出数少，即低风险状态下VaR模型更容易捕捉到异常波动；在收益率波动加大区域，正好反过来。该结论与王春峰等[13]和杨坤等[24]的研究结果相似，表明高风险状态下ES模型比VaR模型表现更优异，它能弥补VaR模型失控的缺陷。

4.5量化交易应用讨论

前文利用跳跃、好坏波动和符号跳跃等新型高频波动率建模预测已实现波动率，并将HAR类波动预测模型融入极值理论，构建测量股指期货尾部风险的RV-EVT风险测量方法，该方法在一定置信水平下测量资产收益率预期水平的临界值。在程序化交易过程中，当拥有稳健的量化交易策略后，将其用于实盘交易时需要计算每次下单的头寸规模，这就是资金管理[49]。

在期货投资实务中，资金管理策略通常可分为固定资金、固定仓位和固定风险策略。固定资金即交易策略的每笔交易都按相同本金计算头寸规模，如100万元人民币的保证金。随着资产价格上涨(资产价值变大)，固定本金允许的头寸会减少。由于上市以来股指期货价格变化较大(见图1)，固定资金策略普适性不强。固定仓位是指交易策略的每笔交易都遵循相同的头寸规模，如10手。固定仓位在不同波动的行情面临的风险差异较大，股指期货波动较大时，固定仓位也不具有普适性。固定风险是指每笔交易按相同损失预期计算动态头寸，动态头寸在不同波动状态下具有较好的适应性。

在RV-EVT尾部风险测量基础上，本研究建立固定风险资金管理策略。假定mon为每笔交易允许的亏损金额，los为每笔交易的期望损失，则固定风险的头寸规模为

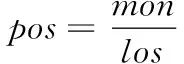
(50)

其中，pos为固定风险的头寸规模。

此时，若每笔交易的允许亏损金额相同，且利用交易策略的平均亏损估计期望损失，则(50)式可归结为固定仓位策略。考虑到资产收益率尾部风险的变化，本研究将其修正为

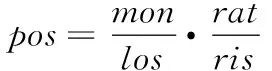
(51)

其中，rat为风险调整系数，ris为风险测量水平。分析(51)式可知，当尾部风险增加(波动率较大)时，计算的头寸减小；当尾部风险减小(波动率较小)时，计算的头寸增大。可见，该资金管理策略的核心是利用尾部风险水平对头寸进行动态调整。因此，本研究建立的资金管理策略是固定风险策略，其优点是经济意义明确且具有可操作性。

现以股指期货的量化交易策略为例，探讨上述资金管理策略的有效性。在讨论资金管理策略之前，本研究设计了成熟的量化交易策略，其历史回测表现见表7。该策略的回测时间为2010年4月16日至2018年8月18日，固定1手的资金曲线见图5(a)。该交易策略包含了做多和做空。当沪深300股指期货为3 000点时，每点为300元(货币种类为人民币，下同)，则每手股指期货的价值为3 000×300=90万元。若股指期货的保证金比例为20%，则每手所需保证金为90万元×20%=18万元。鉴于不同期货公司要求的保证金比例不同，下文在资金管理讨论中假定保证金是充足的。

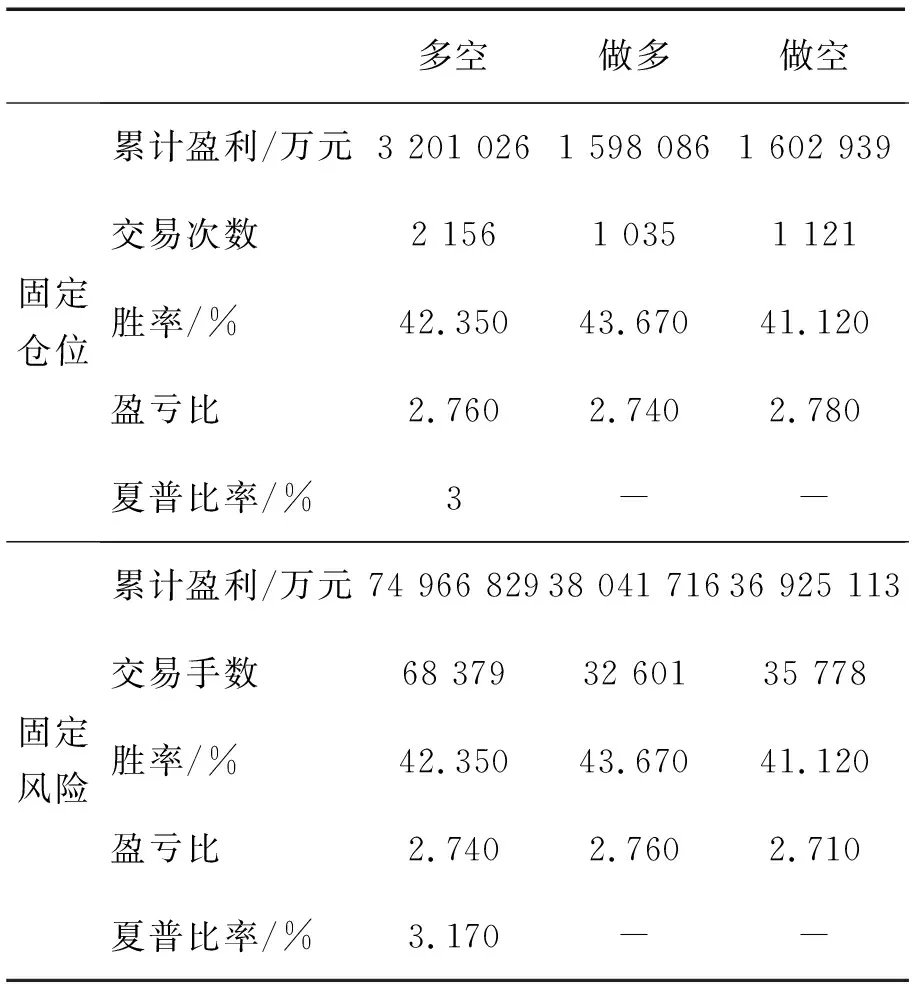
表7两种资金管理方法的量化交易策略回测分析结果Table 7Backtesting Analysis Results for Quantitative Trading Strategies Based on Two Money Management Methods

注：手续费设定为成交金额的万分之1加2跳滑点。

股指期货交易策略的平均亏损为2 512.80元，设定每笔交易允许的亏损金额为5万元，本研究用其估算每笔交易的期望损失。将风险调整系数设定为5%，以RV-EVT框架下的HAR-RV-SJd模型测量的日度ES作为ris，按资金管理(51)式计算的pos作为交易策略的动态头寸，回测得到的策略曲线见图5(b)。其中，做多的头寸计算取下尾ES的绝对值，做空时取上尾ES。由表7可知，固定仓位策略的夏普比率为3，而考虑资金管理的固定风险夏普比率为3.170。分析图5可知，固定仓位策略的曲线存在横向徘徊(固定1手与固定10手的曲线走势相同)，而固定风险资金管理方法策略的曲线近似直线。回顾(51)式，当尾部风险为恒定风险(如-3%)，则该公式退化为固定仓位策略。可见，尾部风险的宽窄变化具有重要价值。综上分析，考虑尾部风险的资金管理策略，使股指期货量化交易策略拥有更高的夏普比率和更稳健的资金曲线。

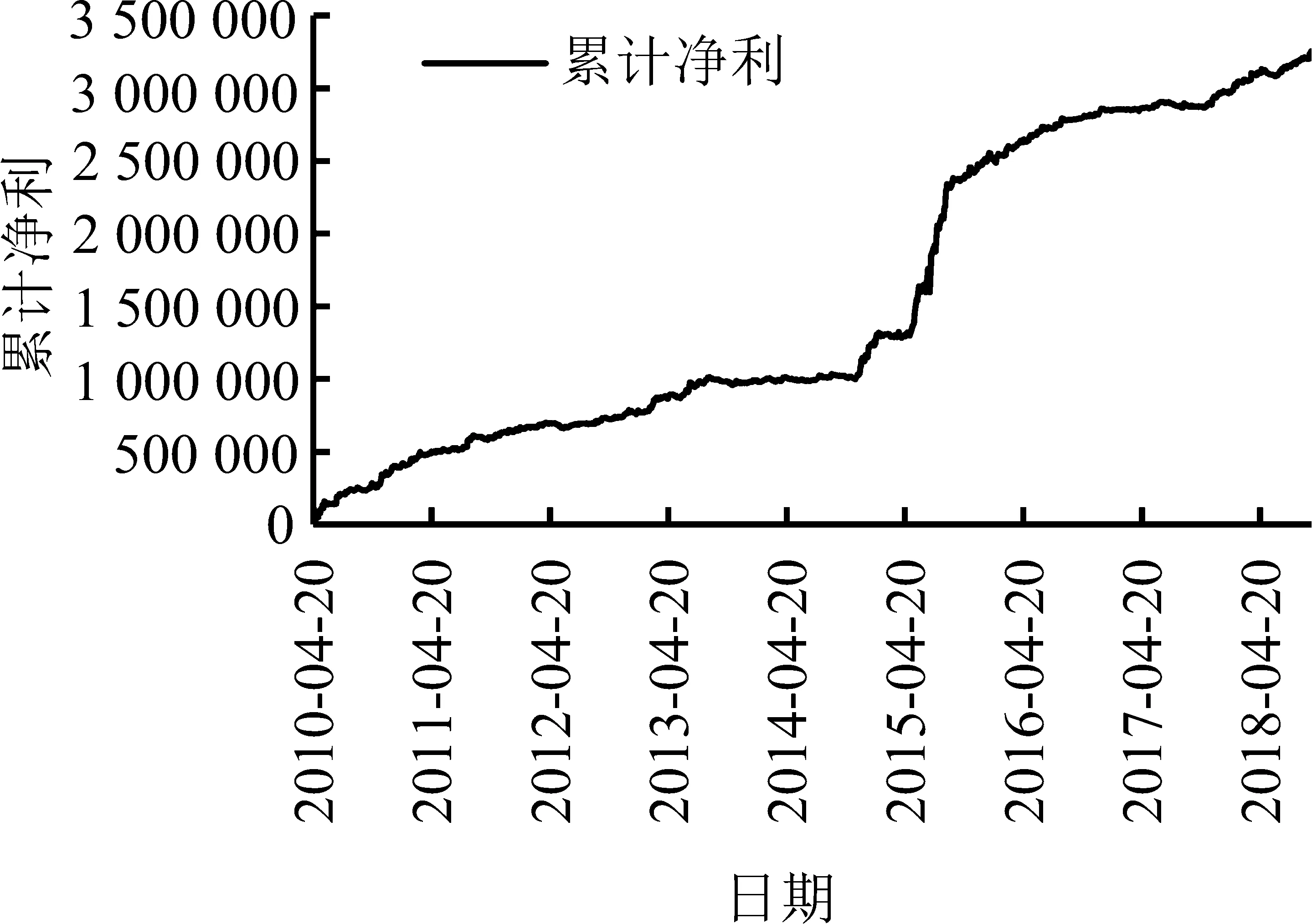
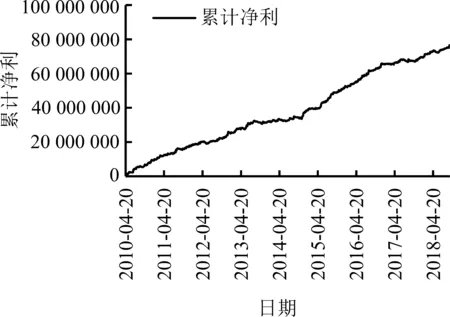
(a)固定仓位策略的资金曲线(b)固定风险策略的资金曲线

因此，本研究探讨的资金管理方法适用于单个资产(或策略)的头寸计算，其充分表明尾部风险在资金管理中的应用价值。当多个资产(或策略)的投资组合需动态评估每个资产(或策略)的风险时，可以利用尾部风险，得到更稳健的资产配置策略。限于篇幅本研究不予展开。

5结论

本研究利用跳跃、好坏波动和符号跳跃等新型高频波动率建模预测已实现波动率，并将预测模型融入极值理论，构建RV-EVT尾部风险测量方法，得到以下研究结果。

(1)波动率的样本外滚动预测表明，HAR波动预测框架下好坏波动分解优于连续跳跃波动分解，好坏波动衍生出的(正负)符号跳跃具有极为突出的波动预测能力；

(2)回测分析检验结果显著,尾部超出数接近理论预期，表明RV-EVT尾部风险测量方法有效；

(3)波动预测模型的精度越高，尾部风险测量水平越佳，HAR-RV-RS和HAR-RV-SJd模型的尾部风险测量水平最佳；

(4)回测分析结果表明，ES模型比VaR模型具有更优的尾部风险测量水平，在高风险状态下ES模型能弥补VaR模型易失控的缺陷；

(5)通过股指期货量化策略的资金管理研究，揭示了RV-EVT风险测量方法的应用价值。

本研究在RV-EVT风险测量框架下完善了已实现波动率的预测建模，在量化交易策略基础上，利用尾部风险建立有效的资金管理策略。本研究建立了高频波动率与风险管理的桥梁，为金融资产尾部风险测量提供了有效方法，对资金管理和风险控制具有借鉴意义。

本研究的理论启示在于，①RV-EVT风险测量框架下VaR和ES模型的建模核心是准确预测未来波动率，而已实现波动率的预测建模具有天然的优势；②根据极值理论推导的VaR和ES估计量，通过多期波动率的预测可实现多期尾部风险的测量。本研究的实践启示在于，①尾部风险的测量在特定置信水平上测量了资产收益损失水平的临界值，它对组合管理、仓位管理等投资实务具有重要的指导意义；②在实务运用中出于量化投资的可靠性需求，VaR和ES的尾部参数可合理假定，或者简化为波动率的调整系数。

本研究难免存在局限性。本研究仅研究单个资产风险测量和实务应用，而投资组合管理需考虑多类资产的风险。因此，不同资产的风险测量和风险传染对大类资产配置的影响是未来研究工作。

致谢

感谢嘉实集团董事长赵学军博士对波动率的独到见解，启发了做空波动率的思考。感谢嘉实基金董事总经理、基金经理张自力博士对barra风险模型的经验分享，使本研究延伸到股票风险建模运用。