“坏”跳跃、“好”跳跃与高频波动率预测

陈国进，丁 杰，赵向琴

1 厦门大学 经济学院，福建 厦门 361005 2 厦门大学 王亚南经济研究院，福建 厦门 361005

引言

在资产组合配置和风险管理领域，对资产波动率的预测一直是人们关注的话题之一。有效的波动率预测的基础在于如何准确地测量波动率，随着大数据时代的来临，我们能够获得资产高频价格数据并基于此更好地测量和预测波动率。基于股市高频数据的波动率预测领域的研究中，学者们一般使用高频收益率的偶函数(如取平方值或者取绝对值)获得各种测量波动率的指标。但是，股市中存在诸多不对称现象，其中之一就是杠杆效应，即不同方向的收益率冲击对波动率产生不对称的影响。借鉴杠杆效应的思想，使用偶函数的做法忽略了日内收益率的正负符号信息(偶函数下正负符号被同等对待)。因此，有必要利用高频收益率的正负符号信息刻画波动率的不对称性。

股价跳跃是股价波动的重要组成部分[1-2]，相应地，有必要利用高频收益率的正负符号信息拆分出两种不同方向的跳跃。风险规避者厌恶资产的波动，如果一种跳跃能够使资产未来的波动率下降，可以把这种跳跃视为“好”跳跃；与之相对应，如果一种跳跃使资产未来的波动率上升，可以把这种跳跃视为“坏”跳跃。本研究探讨这两种不同方向的跳跃是否对波动率产生不对称影响，并考察这种区分跳跃方向的做法是否改进了对波动率的预测能力。

1相关研究评述

1.1波动率的测量和预测

在过去的几十年，关于波动率估计量研究的巨大进展使我们能够更为准确地测量波动率。梳理已有研究成果，测量波动率的方法主要有基于统计模型的波动率、隐含波动率和已实现波动率3类。波动率的统计模型主要有自回归条件异方差族(ARCH)模型[3-4]和随机波动率(SV)模型[5]，这类方法的缺陷在于它们是基于模型获得的，不可避免地存在模型误差。隐含波动率[6-7]根据资产定价模型(如BS模型)从金融产品市场价格中反推出其对应的波动率。由于提取隐含波动率的重要金融产品为期权，其在中国开展时间较短，产品种类较少，市场活跃度有待提高，所以其市场定价机制尚未完善，相应得到的波动率的准确性也有待提高。因此，中国的这类研究比较有限[8-10]。已实现波动率[11-12]使用无模型的方法测量波动率，它的优势在于充分利用日内收益率的高频信息，因而测量更为精准[13]。在当今大数据时代下，分钟甚至分笔高频交易数据的可获得性越发凸显了无模型测量方法的优势。

与此同时，学者们基于高频数据在波动率预测领域进行研究。陈浪南等[14]利用自适应的不对称HAR-CJ-D-FIGARCH模型，马丹等[15]采用门限预平均实现波动率的方法，文凤华等[16]考虑市场波动的杠杆效应和量价关系，构建基于已实现波动率和交易量的长记忆异质自回归模型。虽然以上研究使用不同的模型方法，但都证明高频数据有助于预测股票波动率。需要指出的是，以上研究并没有涉及股价跳跃。因此，一个改进的方向在于充分考虑股价跳跃的信息。

1.2股价跳跃

近年来，很多学者开始关注股价跳跃因素与股票波动率预测、波动率特征、股票收益率解释和预测以及收益率特征[17]。

在跳跃与股票指数波动率预测领域，王春峰等[18]使用HAR-RV-CJ模型证明二次变差中的连续运动部分在中国股市已实现方差预测方面起到重要作用。进一步，孙洁[19]考虑包含跳跃和隔夜波动的日波动率，并且通过基于HAR-CJN模型再一次证实连续运动部分有助于改进波动率预测。此外，该研究另一大贡献在于指出跳跃部分同样对波动率具有不错的预测能力。XU et al.[20]同时引入跳跃因素和杠杆效应这两大因素改进股票波动率的预测，结果表明跳跃能够对股票波动率的预测有帮助。

类似地，部分学者将该应用扩展到期货领域。WEN et al.[21]在带有结构突变的HAR模型的框架下，利用波动率和跳跃预测原油期货的波动率；罗嘉雯等[22]通过构建贝叶斯动态潜在因子模型提取跳跃变量，并基于此预测中国金融期货市场波动率；陈声利等[23]通过单级纠偏HARQ类模型和多级纠偏HARQF类模型研究跳跃能否改进股指期货的波动率预测。以上的研究同样支持跳跃能够改进波动率预测的观点。

在跳跃与股票波动率特征领域，陈国进等[24]利用高频数据剥离出已实现方差中的跳跃性波动时间序列，研究表明中国A股的跳跃性波动比美国市场具有更为长期的滞后相关性；西村友作等[25]同样研究中美两国的波动跳跃特征，但关注对象是全球金融危机时期；宫晓莉等[26]分析中国股指期货和现货市场各自的跳跃和波动行为特征以及市场间跳跃和波动的风险关联性。以上一系列研究表明包含跳跃因素有助于更好地刻画股票的波动率特征。

在跳跃与股票收益率解释和预测领域，左浩苗等[27]从高频数据中剥离出跳跃成分，发现跳跃成分对收益率有稳健的预测作用，即跳跃波动与收益率负相关。进一步，陈国进等[28]采用非参数方法估计Fama-French 25个股票组合的已实现跳跃波动率的主要成分，证明已实现跳跃波动率成分在一定程度上可以通过线性方式解释股票组合的横截面收益；MAHEU et al.[29]通过实证研究表明，跳跃因子在股票收益率中被定价，跳跃导致了更高的股票风险溢价。

此外，引入跳跃因素也能够更好地刻画股票收益率特征。瞿慧等[30]的研究表明，收益率、连续波动和跳跃波动之间存在统计上显著的相关性，联合模型能够更为合理地刻画三者之间相关关系，并且提高参数估计的有效性。BOLLERSLEV et al.[31]提出一个新的框架估计金融资产价格的系统性和非系统性的跳跃尾部风险，并指出跳跃风险导致股票在极端事件时的高相关性。

鉴于高频数据在大多数情形下非常小，一般在0左右波动，因此收益率的正负号信息往往容易在研究中被忽视。过去10年，学术界开始关注高频数据正负符号所包含的信息。BOLLERSLEV et al.[32]的研究表明，利用高频收益率正负符号信息能够更好地体现波动率不对称现象；PATTON et al.[33]利用标普500指数和个股数据的实证研究表明，不同方向的股价波动对未来波动率造成不对称的影响。因此，本研究考虑股价跳跃成分和正负号信息，剥离出两种不同方向的跳跃，探讨股价不同方向的跳跃对波动率是否存在不对称影响以及通过剥离出不同方向的跳跃是否能够显著改进对波动率的预测。

2“坏”跳跃、“好”跳跃的测量和假设

对波动率和跳跃的测量。首先考虑对数价格p在k时刻的随机过程，它由连续运动部分和纯跳跃部分组成，即

(1)

其中，pk为k时刻的对数价格；μ为漂移过程；s为时刻，在式中为积分变量；σs为严格为正的右连左极过程；W为标准布朗运动；J为纯跳跃过程。等式右边前两部分体现随机过程的连续运动部分，第3部分体现随机过程的非连续运动的跳跃过程。这个随机过程的二次变差为

(2)

其中，Δps=ps-ps-，ps为s时刻的对数价格，ps-为先于且无限趋近于s时刻的对数价格。由(2)式可知，随机过程的二次变差由两部分组成，第1部分来源于对数价格随机过程的连续运动部分，即积分方差部分；第2部分来源于随机过程的跳跃运动部分。当跳跃发生时，Δps体现跳跃的幅度；当跳跃未发生时，Δps为0。

ANDERSEN et al.[11]引入已实现方差的概念。作为对数价格随机过程的二次变差的估计量，它由高频收益率的平方和求得。本研究假设在时间段[0,k]中，将时间等分成N部分，这样就能够观察到p0,p1,…,pN共(N+1)个对数价格。通过rn=pn-pn-1就可以得到n个对数收益率，rn为第n个对数收益率，n=1,2,…,N。当样本观察值之间的时间间隔足够小时，已实现方差依概率收敛于二次变差，即

(3)

其中，RV为已实现方差。已实现波动率可由已实现方差的平方根得到。

BARNDORFF-NIELSEN et al.[34]提出二次幂变差的概念。与已实现方差不同，二次幂变差依概率收敛于对数价格随机过程中的连续运动部分的二次变差(即积分方差部分)，即

(4)

(5)

BARNDORFF-NIELSEN et al.[35]进一步提出已实现半方差的概念。该估计量分别测量与正收益和负收益相对应的对数价格的波动，该估计量的定义为

(6)

(7)

其中，RS-为已实现负半方差，RS+为已实现正半方差，I{·}为示性函数。这两个变量是对已实现方差的完全分解，即RV=RS-+RS+。已实现半方差的极限形式既包括来源于对数价格随机过程的连续运动部分，也包括其跳跃运动部分，即

(8)

(9)

基于这两个指标，本研究提出假设。

H1已实现负半方差水平与未来一段时间的波动率水平正相关，而已实现正半方差对未来波动率的影响并不显著。

(8)式和(9)式表明极限形式的RS-和RS+各包含一半的积分方差。这有两层意义：①因为RS-和RS+的第1部分是一致的，意味着对已实现方差的完全分解包括3个部分，而不是4个部分，即积分方差部分、正跳跃部分和负跳跃部分。②通过已实现正半方差与已实现负半方差相减，可以消除由连续运动导致的积分方差部分。剩余部分定义为符号跳跃变差，即

(10)

其中，ΔJ2为符号跳跃变差。ΔJ2的一个缺陷在于它没有区分负跳跃部分和正跳跃部分。为了更好地研究两者的区别，需要更进一步分别剥离出已实现负半方差和已实现正半方差中的跳跃部分，本研究使用两种方法实现这个目的。下文以下角标1表示第1种方法，以下角标2表示第2种方法。

(11)

(12)

本研究将ΔJ2-定义为负跳跃变差，将ΔJ2+定义为正跳跃变差。在这种方法下，彻底剥离出负跳跃和正跳跃。

第2种区分负跳跃和正跳跃的方法从符号跳跃变差出发，通过引入一个示性函数实现两部分的区分，即

(13)

(14)

基于负跳跃和正跳跃两个指标，本研究提出假设。

H2与H1中已实现半方差不同，尽管负跳跃水平与未来一段时间的波动率水平正相关，但是正跳跃水平与未来一段时间的波动率水平负相关。

H3“好”跳跃导致未来波动率下降，而连续运动部分的上升导致未来波动率上升，二者效应的总和导致已实现正半方差对未来波动率的影响不显著；“坏”跳跃和连续运动部分的上升都导致未来波动率上升，二者效应的总和为负半方差水平与未来的波动率水平正相关。

对于很多模型而言，虽然样本内数据分析能够尽可能地利用所有可得的信息准确估计参数，以及得到不错的样本内拟合结果，但是样本外预测才是评估变量是否真正具有预测能力的更为适合的标准。因此，本研究提出假设。

H4利用“坏”跳跃和“好”跳跃不但能够更好地拟合样本内的未来波动率(样本内预测)，还能明显地改善波动率的样本外预测能力。

3数据描述和实证模型

3.1数据来源及其描述

本研究选取的实证数据的时间范围为2012年1月4日(2012年第一个交易日)至2016年12月30日(2016年最后一个交易日)，使用的高频数据来源于国泰安高频数据库，主要实证结果基于沪深300指数高频数据得到。该指数覆盖沪深两市，具有较好的市场代表性，并且本研究同样考察上证综指和深证成指，并得到较为一致的结论。在本研究中高频数据的抽样频率为5分钟，一方面希望获得尽可能高频的数据以满足极限要求，另一方面希望降低数据抽样频率以避免市场微观噪音，选择数据频率为5分钟可以平衡这两者。本研究高频数据对应的交易时间段为9:30～11:30和13:00～15:00，因此在一个交易日内得到48个高频收益率数据。

沪深300指数的波动率(或方差)和跳跃测量的变量的描述性统计结果见表1。由表1的前4行可知，波动率存在明显的右偏和尖峰厚尾特征；由表1的后3行可知，跳跃也存在明显的尖峰厚尾特征。此外，对比表1的前4行和后3行可以发现，已实现方差和已实现半方差中连续运动部分(由二次幂变差体现)的比重较大，而跳跃部分的比重较小。

表2给出沪深300指数波动率和跳跃测量的变量的相关系数。由于连续运动部分比重较大，很自然地推测已实现方差与二次幂变差相关性很高。由于已实现方差、已实现负半方差和已实现正半方差都包括积分方差部分，所以三者的相关性也较强。与此相对应，跳跃部分与已实现方差之间的相关性较弱，表明可以从跳跃中提取新的信息。由于负跳跃变差是已实现负半方差的组成部分，因此两者之间存在一定的正相关性；正跳跃变差和已实现正半方差也是如此。

3.2实证模型

预测波动率的一个常用模型是异方差条件自回归(heterogeneous autoregression,HAR)模型[36-38]，本研究也采用该模型。HAR模型实质上是带限制条件的高阶自回归模型，在已有研究中，该模型的典型模式为利用过去1天、1周(5个工作日)和1个月(约22个工作日)的信息对未来实现值进行自回归分析。本研究使用的HAR模型表达式为

(15)

表1描述性统计结果Table 1Results for Descriptive Statistics

注：为了显示方便，表中数据被放大10 000倍。

表2相关系数Table 2Correlation Coefficients

本研究在回归中使用的变量为波动率(或方差)，而该变量在时间序列上的变化较为剧烈，所以简单地使用OLS方法会使估计过分重视高波动率时期而忽视低波动率时期。因此，本研究使用加权最小二乘(weighted least square,WLS)方法进行估计，通过两步法实现：第1步用OLS方法对模型进行估计，得到被预测变量的拟合值；第2步将被预测变量的拟合值的倒数作为权重，对模型重新进行估计，得到最终的系数估计值。考虑到依然可能存在的异方差和条件自回归特性，本研究使用Newey-West t统计量进行统计推断。

4已实现半方差与波动率预测的实证研究

本研究考察已实现半方差(包括已实现负半方差和已实现正半方差)对波动率的预测能力。预测波动率的基准模型为标准HAR模型，其表达式为

(16)

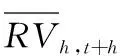
表3给出对已实现半方差和波动率的估计结果。表3由4部分组成，分别对应预测期长度为1天、5天(对应1周)、22天(对应1个月)和66天(对应3个月)，前3个预测期长度与滞后信息时间长度相对应。标准HAR的结果出现在表3各个部分的第1行，除1天的φm值外，其他3个预测期系数的估计值均在1%水平上显著。此外，正如ANDERSEN et al.[12]提到的，已实现方差体现了高持续性特征，即(φd+φw+φm)接近于1。同时，本研究注意到这种持续性随着预测期的延长而减弱。预测期为1天时，(φd+φw+φm)=0.931；预测期为66天时，三者之和下降到0.565。此外，还有一个有趣的发现，随着预测期的延长，φd和φw呈现出单调递减的趋势，而φm呈现出上升的趋势。预测期长度为1天时，φd最大，φm最小，随着预测期的延长这种情况发生逆转。这表明基于过去较短时间(如过去1天或者过去1周)的信息对未来较短期的波动率有更好的解释能力，而基于过去较长时间(如过去1个月)的信息对未来较长期的波动率有更好的解释能力。为了研究利用日内波动方向的收益率信息是否有助于更好地预测未来波动率，本研究将RV分解为RS-和RS+两部分，表达式为

(17)

用(17)式进行估计的结果见表3各预测期的第2行，可以看到，无论预测期为多长，负半方差的系数估计值都为正，数值明显大于正半方差的系数估计值的绝对值，除1天的φm值外，其他3个预测期系数的估计值均在1%水平上显著。正半方差的系数估计值符号不一致，在预测期为1天、22天和66天时，系数估计值的符号为负；在预测期为5天时，系数估计值为正。此外，它们在统计上都不显著。以上的实证结果表明H1得到验证。

表3已实现半方差与波动率预测结果Table 3Results for Realized Semivariance and Volatility Forecasting

注：括号中数据为系数估计值的Newey-West t统计量；***为在1%水平上显著，**为在5%水平上显著。下同。

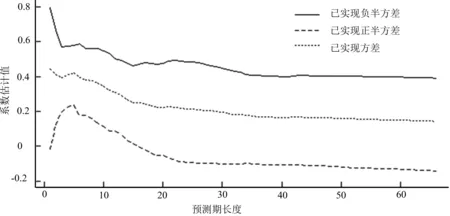
图1已实现方差和已实现半方差的系数估计值Figure 1Estimated Coefficients of Realized Variance and Semivariance

5“坏”跳跃、“好”跳跃与波动率预测的实证研究

5.1波动率的样本内预测

由上文可知，将已实现方差分解为已实现负半方差和已实现正半方差对预测未来波动率起到重要的作用，已实现负半方差包含的能够预测波动率的信息大于已实现正半方差包含的信息，已实现负半方差和已实现正半方差的极限形式都是由两部分组成，它们的第1部分是完全一致的，皆为二分之一的积分方差。所以，二者所产生的影响的差异仅源于它们不同的第2部分，即跳跃导致的股价波动部分。描述性统计结果表明，跳跃部分占已实现方差和已实现半方差的比重比较小，所以一个令人担心的问题是比重较大的连续运动部分的存在是否会稀释股价跳跃所产生的影响，本研究对此进行探讨。

使用符号跳跃变差研究这个问题，即ΔJ2≡RS+-RS-，该方法在理论上能够消除连续运动部分而只剩下了跳跃部分。如果一天中发生的跳跃主要是向下跳跃，该变量的数值为负；如果一天中发生的跳跃主要是向上跳跃，该变量的数值为正。使用该方法的好处是它在技术上的简单性，只要将已实现正半方差和已实现负半方差相减就可以得到。

本研究使用的参照模型为

(18)

在(18)式中，滞后1天的波动率信息仅包含其连续运动部分(用二次幂变差表示)，预测结果见表4各预测期的第1行。表4给出“坏”跳跃和“好”跳跃与波动率的预测结果。与表3一样，表4也由4个部分组成，分别对应预测期为1天、5天、22天和66天。由于连续运动部分占已实现方差的比重较大，回归结果与表3基准模型的结果类似，除1天的φm值外，其他系数的估计值均在1%水平上显著。

本研究探讨包含符号跳跃变差的模型，即

(19)

表4“坏”跳跃、“好”跳跃与波动率预测结果Table 4Results for “Bad” Jump, “Good” Jump and Volatility Forecasting

注：*为在10%水平上显著，下同。

为了区分出跳跃部分和连续运动部分对未来波动率的影响，(19)式既包括跳跃部分(用符号跳跃变差表示)，也包括连续运动部分(用二次幂变差表示)，预测结果见表4各预测期的第2行，可以发现，符号跳跃变差的系数φJ的估计值在4个预测期皆为负且都在统计上显著。这表明，如果一天中的跳跃主要由负跳跃构成，这样的日子对应未来更高的波动率；如果一天中的跳跃主要由正跳跃构成，这样的日子对应未来更低的波动率。由此，进一步推断出，负跳跃导致未来波动率上升而正跳跃导致未来波动率下降。这个结论与ANDERSEN et al.[37]的研究结果不同，他们的实证结果显示不区分方向的跳跃会导致未来标准普尔500指数波动率略微下降。而上文的分析表明ANDERSEN et al.[37]不区分跳跃方向的做法忽略了负跳跃和正跳跃对未来波动率造成的截然不同的影响，引入符号跳跃变差能够提供关于波动率预测的更多信息。

(20)

还要提及的一点是，前文的实证表明负半方差显著导致未来波动率上升，正半方差对未来波动率的影响在统计上和经济上并不显著，在极限形式下二者的差异仅在于其跳跃部分的不同。通过引入负跳跃变差和正跳跃变差，本研究可以发现，不但负跳跃对未来波动率产生显著影响，正跳跃也会对未来波动率产生显著影响，二者在影响方向上恰好相反。

图2负跳跃变差和正跳跃变差的系数估计值Figure 2Estimated Coefficients of Negative and Positive Jump Variations

正半方差与正跳跃之间在统计显著性上的差异来源于连续运动部分，二次幂变差(体现连续运动部分)的系数估计值为正(见表4的φc)，正跳跃变差的系数估计值为负，这二者效应的叠加导致已实现正半方差的系数估计值在经济上和统计上不显著。因此，正是连续运动部分稀释和掩盖了正跳跃对未来波动率的影响。与之相反，二次幂变差和负跳跃变差的系数估计值皆为正，这二者效应叠加导致已实现负半方差的系数估计值为正且在经济上和统计上都显著。由此，H3得到验证。由于股价的负跳跃导致未来波动率上升，而风险规避者厌恶高波动率，所以本研究将负跳跃称为“坏”跳跃；股价的正跳跃导致未来波动率下降，而风险规避者偏好低波动率，所以本研究将正跳跃称为“好”跳跃。

5.2波动率的样本外预测

本研究使用的比较方法如下：第1步，对被预测变量和预测变量的前100个样本观测值做回归并得到系数估计值；第2步，利用得到的系数估计值和预测变量第101个样本观测值得到第101个被预测变量的预测值；第3步，将被预测变量第101个实际观测值和第2步中得到其预测值相减得到其预测误差；第4步，重复前3步的工作，逐一延长用于参数估计的回归中使用的观测值的样本量，不断利用更新的系数估计值和新一期的预测变量的观测值得到下一个被预测变量的预测值，并计算相应的预测误差。

需要指出的是，关于最初模型参数估计的样本长度(前100个样本)的选择是基于模型参数估计的准确性(即足够长的时间序列用于估计)和产生足够长的预测值的时间序列这两者之间的平衡。对于得到的预测值和预测误差，本研究使用两种方法比较其预测结果的优劣。

第1种方法使用DM统计量[39]，表达式为

(21)

两两对比8组样本外预测结果。由表5第2列和第3列可知，在这两组4个预测期共8个结果中，DM统计量皆为正，且其中6个结果的原假设在5%显著性水平上被拒绝，其中7个结果的原假设在10%显著性水平上被拒绝，这表明对RV的拆分有助于改善样本外预测能力。由表5第4列和第5列可知，在这8个结果中，DM统计量皆为正，且其中5个结果的原假设在5%显著性水平上被拒绝，这表明充分利用1天内价格变动的高频信息比仅利用1天总收益率的正负号的单一信息能得到更好的样本外预测效果。由表5第6列和第7列可知，在这8个结果中，有6个结果的DM统计量为正，且其中2个结果的原假设在5%显著性水平上被拒绝，4个结果的原假设在10%显著性水平上被拒绝，这在一定程度上表明利用包含股价跳跃部分的信息以及日内波动方向的信息比仅利用股价连续运动部分的信息能够得到更好的样本外预测结果。为了进一步清楚比较跳跃信息的样本外预测作用，由表5第8列和第9列可知，除预测期为5天的情形，其他结果的原假设都在5%显著性水平上被拒绝。以上结果表明，充分利用跳跃方向的信息能够获得更好的样本外预测效果。

(22)

表5DM统计量Table 5DM Statistics

表6样本外Table 6Out-of-Sample

6稳健性检验

6.1利用完整的滞后信息

前文的实证结果是基于仅仅利用滞后1天的日内收益率正负符号信息得到的，下面进一步拓展日内收益率正负符号信息来源的时间段。本研究考察同时利用滞后1天、滞后1周和滞后1个月的负跳跃变差和正跳跃变差以及二次幂变差信息的情形。在这种利用完整的滞后信息情况下的表达式为

(23)

用(23)式进行估计的结果见表7，回归结果再次证明负跳跃导致未来波动率上升而正跳跃导致未来波动率下降。在完整利用滞后1天、滞后1周和滞后1个月的日内收益率正负符号信息的情形下，前文的实证结果不变。

6.2负跳跃变差和正跳跃变差的第2种定义

上文的实证结果是基于负跳跃变差和正跳跃变差的第1种定义得到的，下面探讨在使用二者的第2种定义时实证结果是否会发生改变。相应的表达式

变为

(24)

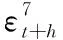
表7完整滞后信息下的负跳跃变差、正跳跃变差与波动率预测结果Table 7Results for Negative Jump Variation, Positive Jump Variation and Volatility Forecasting under Complete Lag Information

表8负跳跃变差和正跳跃变差的第2种定义Table 8The Second Definition of Negative Jump Variation and Positive Jump Variation

采用(24)式的估计结果见表8。由表8可知，负跳跃变差的系数估计值全部为正，正跳跃变差的系数估计值全部为负，且大多数情形下两者在统计上显著。再一次表明负跳跃会导致未来波动率上升，正跳跃会导致未来波动率下降，进一步支持上文的结果。

7结论

由于已实现方差中的连续运动部分比重较大，一个令人担心的问题是跳跃部分对未来波动率的影响会被稀释。因此，本研究专门剥离出负跳跃和正跳跃，并基于此研究其是否有助于改进中国股市的波动率预测，得到以下结论。

(1)基于HAR模型的实证结果表明，已实现负半方差水平与未来一段时间(本研究考虑未来1天至未来3个月的情形)的波动率水平正相关，且该结果在统计上和经济上显著，而已实现正半方差对未来一段时间波动率的影响在统计上和经济上不显著。

(2)负跳跃水平与未来波动率水平正相关，正跳跃水平与未来波动率水平负相关。由于风险规避者厌恶波动，因此本研究将这两者分别称为“坏”跳跃和“好”跳跃。

(3)“好”跳跃导致未来波动率下降，而连续运动部分的上升导致未来波动率上升，二者效应的总和导致已实现正半方差对未来波动率的影响不显著。“坏”跳跃和连续运动部分的上升都将导致未来波动率上升，二者效应的总和导致已实现负半方差对未来波动率产生显著的正影响。

本研究的学术贡献为：①利用日内收益率的正负符号信息，并基于此提取和剥离两种不同方向的跳跃。②实证研究证明“坏”跳跃和“好”跳跃会对波动率产生不对称影响，而这一点是不区分方向的跳跃无法体现的。由于“坏”跳跃和“好”跳跃对波动率产生相反方向的影响，因此对跳跃方向不加区分会大大削弱跳跃的实际影响。③利用一系列的统计指标证明“坏”跳跃和“好”跳跃能够明显改进波动率的样本内和样本外预测能力，进一步丰富了波动率预测方面的研究。

本研究还存在不足之处，对于负跳跃和正跳跃的研究仅涉及波动率预测领域。事实上，它在金融领域可能还有更多可研究和应用的地方，包括利用负跳跃和正跳跃是否能够优化组合配置以及是否有助于金融资产风险控制等，这些方向有待于后续进一步的研究。