浅谈高中数学中数形结合法的运用探讨
由文心
(吉林省临江市第二中学)
在实际数学教学中,教师所采用的方法是多种多样的,但是考虑到数学课程自身抽象性的特点,数形结合的教学思想是受到更多的数学教师认可的。在数学教学实践中,大多数老师都会采用数形结合的思想来展开整节课的讲解,通过数形结合提高学生的理解水平,帮助学生解决遇到的各种难题。所以本文主要就是分析在实际的数学教学中数形结合思想的实际应用。
一、数形结合解决集合问题
集合问题是高中数学的入门内容,同时也是高中数学的基础。在集合这一内容中包含了数学中的很多理念。但是由于集合本身所具有的逻辑性,使得很多学生在学习集合的过程中出现问题。而数形结合思想的应用有效地解决了这些问题。究其原因,主要是集合中的大部分知识,比如关系交集、并集以及补集等等都是间接地和图形相互联系的,并且基础的表达式比如{A,B,C}也与图形息息相关。在实际的解题过程中,数形结合的思想能够有效地解决集合的问题,换言之,就是将集合关系转化成为关系图形,这样更加形象化,有利于学生的理解。
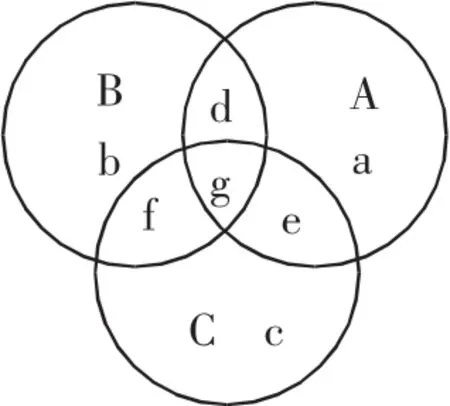
正如平时所常用到的方法,数形结合在解决集合问题的时候是以两种方式体现的,一种就是数轴,这是很有效且很方便的一种图形。而另外一种则是韦恩图。与数轴相比,韦恩图能够更加清晰地展示出各个集合之间存在的关系,使得最后的结合更加直观和形象,而数轴仅仅是能够表示出大概的关系。比如,在对集合A和集合B之间存在的包含关系分析的时候,由于其中关系到了不等式的问题,所以利用数轴的方法更加简单和直接。而用韦恩图进行分析的问题一般都是趋向于数型集合这类问题,这种方法能够更加具体地将条件以图形的形式展示出来。
例如一道题目:“在一次学校组织的数学竞赛中,总共给出了三个题目,分别是1,2,3。那么参赛的人数总共有25个,其中所有的人都必须至少选做一个题目。最后经过统计可以知道,在1题答错的人数中,答对第2题的人数是答对第3题人数的2倍。而答对第1个题的人数比余下的人数多一个。而只答对一道题目的学生的总人数中有一半的学生没有答对第1题。请问有几个学生答对了第2题?”这个问题在刚开始分析的时候可能会感觉到关系非常复杂,条理也并不是非常清晰,尤其是那些逻辑思维比较差的学生就会感觉难度非常大。但是借助韦恩图进行分析,就会更加直观。其中的三个圆分别表示答出三个题目的人数,比如可以将其中的A、B、C作为每一个题目答对的人数,而a,b,c,d,f,e,g则是代表着答对一个题目以上的人数。随后将题目中的数字带入展开分析即可。
二、数形结合解决方程和不等式问题
在高中数学教学中,最为常见也是最为重要的一个图形工具就是坐标系。由于坐标系的存在,具有高度的空间性以及抽象性的知识都可以变得更加直观,极大地促进了学生对知识的理解。尤其是针对方程以及不等式等的问题,坐标系的存在就发挥了非常大的作用。利用坐标系解决问题的方法主要是通过分析方程或者是不等式两边的式子,将其绘制成坐标图,标注重要的数字及信息,最后通过分析绘制成的图像就能够简化方程和不等式的问题。
比如,在针对这一方程sin2x=log5x的时候,求这一方程的解有多少个?这一问题看似非常复杂,但是学生通过分析方程,并将其绘制成坐标系图,直接将两边的函数绘制成两个图像,最后只需要观察这两个图像之间有多少个相交的点即可得到答案,不仅方便解答,而且准确度高。
三、数形结合解决函数极值问题
在高中阶段,函数的极值问题也是这一节内容中常见的题目,而极值的求解就是不等式的解决方法,即借助图形绘制来完成。
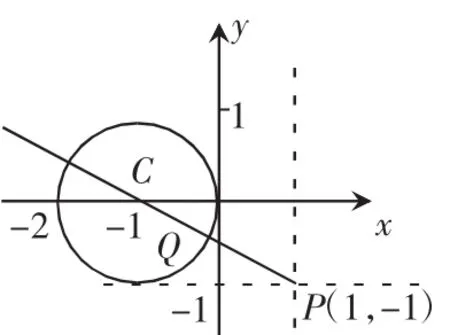
比如,对于不等式(a+b)2≥0,想要求得最后的极值,那么最简单的方法就是将这一不等式转化为图形的形式,不仅可以减少不必要的大量的计算,还能够有效地提升准确率。
又如,方程 x2+y2+2x=0,求(x-1)2+(y+1)2的最小值。如果对于这道题用普通的计算方法,那么计算的过程是非常复杂的,首先要从第一个方程给出的条件中确定x与y的关系以及两者的取值范围,随后还要借助第二个方程进行大量的运算。而在实际的解题中,学生在计算中经常会出现很多的问题,降低准确率。所以可以利用数形结合的思想,绘制出如上图所示的图形,这样就有效地将极值问题转化为了图形问题。
综上所述,数形结合的思想在高中数学中的应用是非常广泛的,能够极大地减少不必要的计算,降低问题的复杂程度,提高计算的准确率。数形结合在以后的高中数学教学中应该被广泛地采用,使问题更加直观,高中数学的解题速度极大地提高。
尚军.高中数学教学中数形结合法的应用探讨[J].广西教育,2016(42).

