基于微分控制策略的快速粒子群优化算法
樊吕彬,刘亚红,张 玮
(太原理工大学 化学化工学院,太原 030024)
0 概述
粒子群优化(Particle Swarm Optimization,PSO)算法是一种基于种群全局随机搜索策略的智能进化算法[1]。相比于其他智能算法,粒子群优化算法在解决多目标优化、动态寻优等问题上,具有结构简单、易编程实现等特点,被广泛应用于函数优化、资源配置、神经网络训练和路径选择等多个领域。
为提高粒子群优化算法种群在进化后期的多样性,避免寻优过程陷入局部最优,克服早熟收敛,相关学者提出了多种改进方法,按照改进机制的不同主要是在参数设置[2]、学习机制[3]和拓扑结构[4]等3个方面。
相应的改进算法在避免陷入局部最优上取得了较好的效果,但对于加快算法的寻优速度、提高优化效率,则需要考虑研究算法本身的特性进而找到改进策略。比例-积分-微分(Proportional-Integral-Derivative,PID)控制是目前最常用的控制策略,已大量应用于各种控制问题。受PID控制的启发,文献[5]认为PSO是一种有2个输入和1个输出的反馈控制系统,通过在粒子群优化算法中引入加速度项,使算法进化行为呈现三阶系统特性,增加种群产生的多样性;文献[6]针对PIDPSO引入加速度项后可选参数多的问题,为提高算法的计算效率,使参数随着进化代数而变化,提出了一种自适应PID粒子群算法;文献[7]提出了一种增量型PID控制器PSO(IPID-PSO),通过对粒子轨迹特性的分析,经过变换后将粒子群速度更新机制解释为一个增量型PID控制过程。
本文受前人工作的启发,研究种群寻优过程的运行机制,推导出PSO近似于一种比例-积分(Proportional-Integral,PI)控制,而由于其固有积分属性的存在,使算法收敛速度变慢。为使种群在寻优过程中快速向最优位置搜索,减少与全局最优值之间的偏差,避免寻优过程振荡,通过添加微分项,提出微分控制的改进策略,利用该策略加快标准粒子群及其改进算法的收敛速度,改善搜索特性,提高寻优效率。
1 粒子群算法速度轨迹分析
在标准PSO中,整个种群随机初始化m个粒子,每个粒子根据其速度和位置的不同,随机分配一个速度向量vi(t)和位置向量xi(t)。粒子在多维空间的飞行过程中逐代搜索最优解,其中每个粒子都是潜在解。粒子根据其自身和整个种群所经过的最好适应度值的位置确定下一次飞行的速度和方向,个体所经过的适应度最好位置称为个体最优点pbest,种群经过的适应度最好的位置称为全局最优点gbest。种群根据个体最优点和全局最优点进行逐代进化,其速度更新公式为:
vi,d(t+1)=wvi,d(t)+c1r1(pbesti,d-xi,d(t))+
c2r2(gbestd-xi,d(t))
(1)
种群位置更新公式为:
xi,d(t+1)=xi,d(t)+vi,d(t+1)
(2)
其中,w称为惯性权重,表示对上一代速度的惯性继承。c1和c2为常数,分别称为个体和社会加速因子,用以调节迭代步长。r1和r2为取值在[0,1]之间服从均匀分布的随机数。
2 粒子群优化算法的控制策略分析及改进
2.1 粒子群算法控制策略分析
在标准粒子群算法中,加速因子c1和c2可以平衡种群在进化过程中的全局勘探和局部探索能力,通常取c1=c2=c,则由式(1)得:
(3)
其中,a1为取值在[0,1]之间的随机数,a为取值在[0,2]之间的随机数。
令B(t)=a1pi(t)+(1-a1)pg(t),则B(t)为个体最优值位置与全局最优值位置的矢量和,将其代入式(3)可得:
v(t+1)=wv(t)+ca{B(t)-x(t)}
(4)
根据控制策略理论,将粒子群优化算法视为反馈控制系统,把种群个体作为控制对象,B(t)位置为给定值,个体位置x(t)为测量值,则其反馈控制的系统偏差为e(t)=B(t)-x(t),通过负反馈调节,使粒子的当前位置向最优粒子靠近。
首先假设每次迭代时最优粒子位置B(t)固定,将式(4)带入式(2)中得:
x(t+1)=x(t)+wv(t)+ca{B(t)-x(t)}
(5)
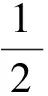
Ex(t+1)-Ex(t)=wEv(t)+c(B′-Ex(t))
(6)
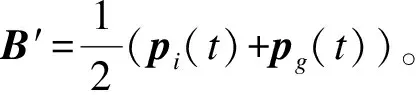
利用式(6)的递推关系可得:
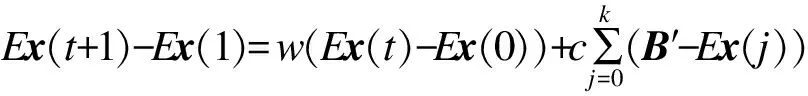
(7)
根据偏差e(t)的定义将上式整理为:
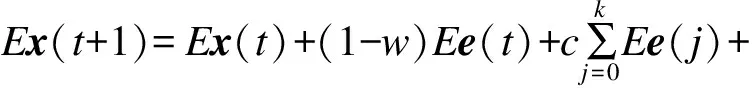
x(1)-wx(0)-(1-w)B′
(8)
则其速度期望为:
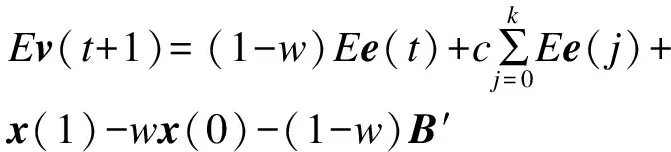
(9)
式(9)通过与PID控制策略的位置型表达式(10)[8]相类比,可得粒子群优化算法的速度更新机制为比例-积分(Proportional-Integral,PI)控制。
(10)
其中,比例项为Kp=1-w,积分项Ki=c,速度初值为x(1)-wx(0)-(1-w)B′。因此可以将标准粒子群算法视为一种比例-积分(PI)控制策略。
2.2 微分项粒子群算法控制策略
文献[9]认为不同的系统性能参数会使粒子群算法的寻优过程呈现出不同性能:超调量越大则种群将会在更大搜索空间中寻优,算法具有更强的探测能力;衰减比越大,则种群将以更快的速度靠近最优值位置,但会减弱粒子群的搜索能力,不利于跳出局部最优。
根据偏差的比例(P)、积分(I)、微分(D)进行控制,是控制系统中应用最为广泛的一种控制规律。经过上节分析可知,粒子群优化算法的寻优过程为比例-积分(PI)控制。若在粒子群优化算法中加入微分控制项,则:
1)微分控制项会减小超调量和衰减比,克服系统振荡,使响应过程更加柔和,提高系统的稳定性。
2)微分控制能够加快系统的响应速度,减小调整时间,使得系统响应快速趋于稳态。
离散化的微分项位置型控制算式为:
D(t)=Kd(e(t)-e(t-1))
(11)
离散控制算式有位置型和增量型2种。位置型控制算式会使偏差逐代累积,同时占用较多的数据储存单元,不利于计算机运算。因此,将微分项的位置型控制算式相减可得增量型控制算式:
ΔD(t)=D(t)-D(t-1)=
Kd(e(t)-e(t-1))-Kd(e(t-1)-e(t-2))=
Kd{(B(t)-x(t))-2(B(t-1)-x(t-1))+
(B(t-2)-x(t-2))
(12)
将上式带入标准粒子群算法的速度迭代方程,可得带微分控制项的速度迭代方程:
(13)
由于在进化过程中通过对标准粒子群算法引入微分项,利用微分控制策略对最优位置的偏差进行反馈调节,因此同样可将微分环节引入到改进粒子群算法中。
通过将微分控制项引入标准粒子群优化(Standard SPO,SPSO)算法及全信息粒子群(Full Information Particle Swarm,FIPS)算法[10],分别可得其改进算法D-SPSO和D-FIPS的速度迭代方程。
D-SPSO算法速度迭代方程为:
vi,d(t+1)=wvi,d(t)+c1r1(pbesti,d-xi,d(t))+
c2r2(gbestd-xi,d(t))+ΔDi
(14)
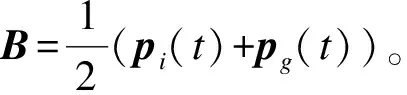
D-FIPS算法速度迭代方程为:
vi,d(t+1)=wvi,d(t)+ck(FIPS(t)-xi,d(t))+ΔDi
(15)
其中,B=FIPS(t)。
2.3 轨迹特性分析
由于粒子群算法在解空间中进行随机搜索,因此搜索轨迹的稳定性是衡量其性能的重要指标[11],以改进算法D-SPSO为例对其搜索轨迹的收敛性进行证明。
定理参数w、c1+c2和Kd满足条件式(16)时,D-SPSO算法是稳定收敛的。
(16)
证明:通过进化方程可以看出,粒子在每一维的更新都是相互独立的,且由于各粒子是随机生成,因此可以将算法设为一维情况进行处理,其结果同样适用于其他粒子。根据降维简化,将式(14)带入式(2),得到如下离散型迭代公式:
xt+3+(c1r1+c2r2-1-w+Kd)xt+2+(w-2Kd)xt+1+
Kdxt-c1r1pbest(t)-c2r2gbest(t)=0
(17)
(18)
根据Z变换平移定理[13]对式(18)进行变换操作,经整理后如下:
(z3+T1z2+T2z+T3)Ex(z)=S
(19)
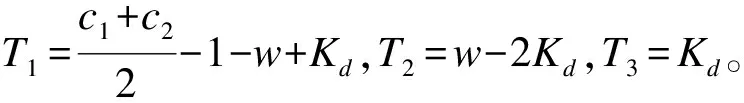
z2[x(1)+T1x(0)]+z[x(2)+T1x(1)+T2x(0)]

Au3+Bu2+Cu+D=S
(20)
其中,A=1+T1+T2+T3,B=3+T1-T2-3T3,C=3-T1-T2+3T3,D=1-T1+T2-T3。
由式(20)可以得出,其特征方程为:
Au3+Bu2+Cu+D=0
(21)
离散系统稳定性判据:在劳斯阵列表第1列元素均大于0,且特征方程各系数均取正值时,系统趋于稳定。
根据离散系统稳定性判据可得,若要使系统趋于稳定,则特征方程式(21)应满足下式:
(22)
即当参数w、c1+c2和Kd满足条件式(22)时,每个粒子的寻优轨迹收敛,种群寻优过程趋于稳定。证毕。
2.4 算法流程
微分控制策略标准粒子群算法D-SPSO的执行流程如图1所示。

图1 D-SPSO算法流程
微分控制策略全信息粒子群算法D-FIPS的执行步骤如下:
步骤1初始化种群,随机生成种群中各粒子位置和速度,并设置各参数值。
步骤2计算种群中每个粒子适应度值。
步骤3更新种群个体最优点pbest及个体最优值pbestval。
步骤4更新种群各邻域中的全信息系数ck及全信息粒子FIPS[10]。
步骤5根据式(12)和式(15)计算微分控制项的增量型控制算式ΔD。
步骤6按照式(15)和式(2)对种群速度和位置进行更新。
步骤7判断是否达到终止条件,若满足,则停止迭代,输出最优值;否则,迭代次数t=t+1,并转至步骤2。
3 实验仿真及性能分析
3.1 仿真实验结果
为了验证微分控制策略的有效性,分别利用标准粒子群算法SPSO和改进算法FIPS进行实验,并选取7个经典测试函数,通过仿真实验分析其性能。测试函数的寻优范围、极值和目标精度如表1所示。
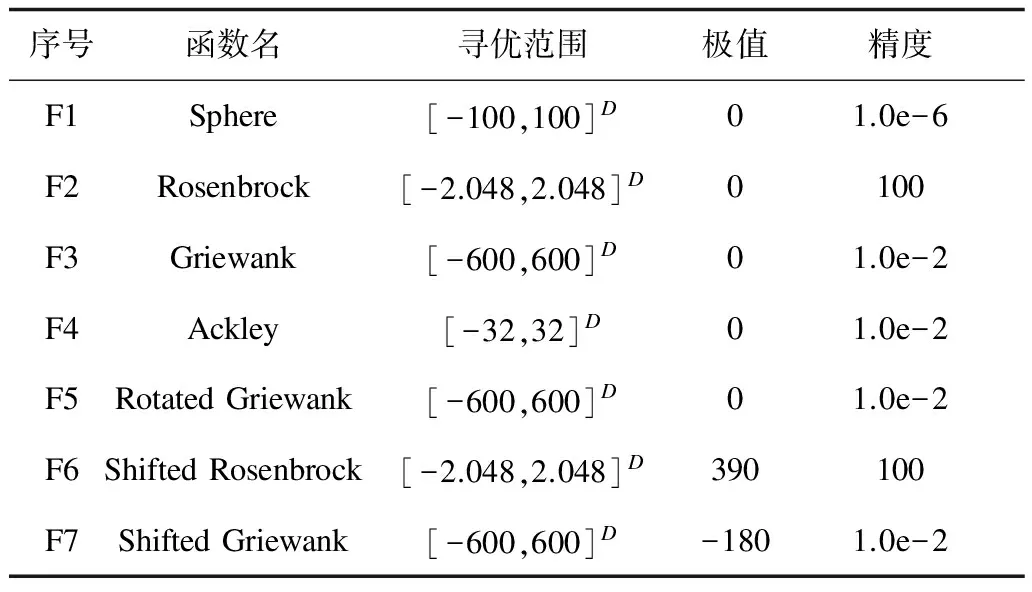
表1 经典测试函数
Sphere为单模态二次函数,在定义域中只有全局极小值点没有局部极小值点,是评价算法收敛精度的经典函数;Rosenbrock为非凸、病态单峰函数,最优点不在空间中心,算法很难辨别搜索方向;Griewank为剧烈震荡的多峰函数,其局部极小值随维数不断增加,在低维空间更难寻优;Ackely为具有大量局部最优点的多峰函数,全局最优解位于一个狭窄区域,多峰函数常用以评价算法跳出局部最优的性能。
在实验过程中,每组实验独立运行30次,种群经过5 000次迭代后停止运行,即达到2.5E+05次函数计算次数(FE)时终止运算。种群规模设为50,在30维空间内进行寻优,粒子的最大寻优速度Vmax通常设置为寻优范围的0.1倍。惯性权重w采用文献[14]提出的线性递减惯性权重策略,以平衡进化过程中的局部和全局搜索能力。
根据轨迹稳定性分析可得:当参数w、c1+c2取值为表2中时,Kd取值为[0,0.2]。分别对微分控制策略的Kd采用阶跃值和固定值,采用阶跃值时,前期较大的Kd有助于增加微分控制的作用,减小系统的超调量,加快收敛速度;后期采用较小的Kd,突出积分项的影响,增加种群的多样性,同时进行精细搜索提高精度,从而在整个过程中提高寻优效率。各算法的参数设置如表2所示。

表2 各算法及参数设置
3.2 算法性能分析
3.2.1 优化精度分析
从表3中的寻优结果来看,相比于标准SPSO,D-SPSO1和D-SPSO2算法对各个函数的适应度均值都有提高,表明在相同的计算次数下,D-SPSO具有更高的计算效率。其中,Mean表示在经过2.5E+05次函数计算后,所得到的平均适应度值,Std表示2.5E+05次函数计算后的标准差,Min表示迭代达到终止条件时,函数所得到的最小适应度值,Imp表示改进算法的平均适应度值提升程度。在方差方面,D-SPSO对函数F1、F2、F4、F7取得的性能上的提高,有助于提高算法的稳定性。同样对于改进算法FIPS,如表4所示,D-FIPS1和D-FIPS2算法对函数F1、F3、F5、F7的适应度均值都有较大提高,且方差优于FIPS,可见微分控制策略不但提高了计算效率也增强了算法的稳定性。
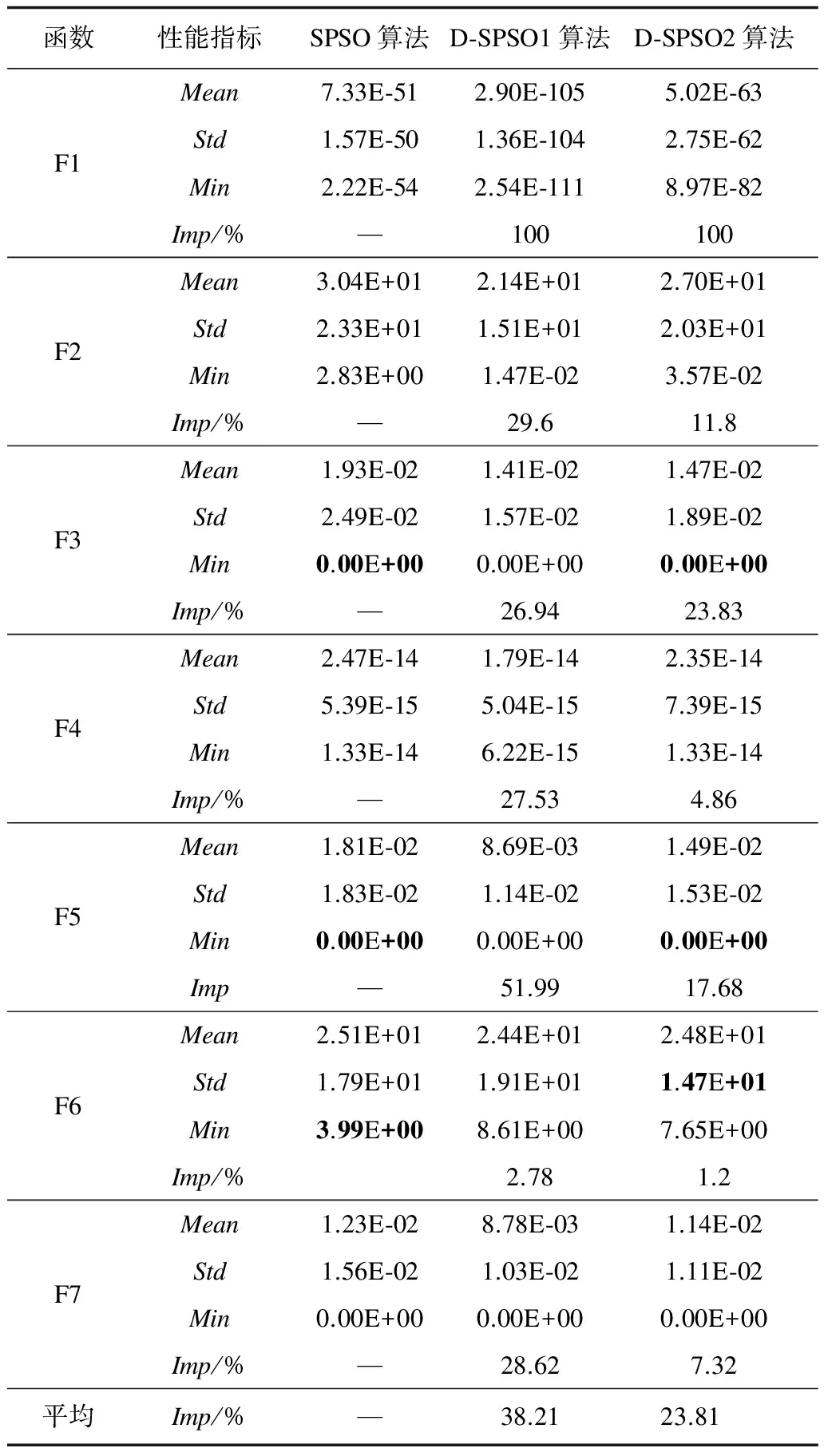
表3 测试函数仿真结果1

表4 测试函数仿真结果2
为便于比较微分策略对粒子群改进算法的性能提高程度,通过适应度均值[15]研究其性能的提升:
(23)
若微分控制改进粒子群算法得到的适应度均值更小,则Imp为正值,否则其为负值。
由表3、表4可以看出,D-SPSO和D-FIPS对原算法的平均适应度均有提高,其中,D-SPSO对函数F1、F2、F4、F5和F7的提高均在30%左右;D-FIPS对函数F1、F3、F5和F7取得了近似于100%的改进效果。对于改进算法较难优化的多峰函数和旋转与偏移函数,D-SPSO和D-FIPS取得了较好的平均适应度提升度。同时根据平均提升度可以看出,在Kd采用阶跃值时,对于优化性能的提升度要高于采用固定值,说明在不同时期微分控制作用的强弱,对粒子群算法性能的改进具有明显的影响。
3.2.2 算法复杂度及平均计算次数分析
算法复杂度[16]是评估算法性能的一个重要指标,决定了算法的寻优速度和优化效率。以标准粒子群算法SPSO为例,设求解问题的维数为D,种群规模为N,最大迭代次数为T。在每次进化过程中,算法主要的计算量包括粒子个体最优位置更新与全局最优位置更新两部分,在引入微分控制策略后,由于位置B(t)为pbest和gbest的矢量和,其更新由后者位置更新来确定。最复杂情况下最大计算时间复杂度为T×O(N×D),保留最优个体的存储空间复杂度为O(N×D),所以该算法的最大复杂度:
O(T,N,D)=T×O(N×D)+O(N×D)
(24)
由式(24)可以得到,相对于基本粒子群算法,在引入微分项后,微分策略的粒子群算法并没有明显地增加算法的复杂度。
图2和图3为各算法在经过30次实验仿真后所需的平均计算次数,其中函数计算次数(FE)反映了各算法在寻优过程中调用测试函数的次数。从图中可以看出:对各测试函数,SPSO和FIPS算法的时间复杂度均最大,在引入微分策略后,使D-SPSO和D-FIPS算法达到寻优要求时的函数计算次数最少,加快了寻优速度。
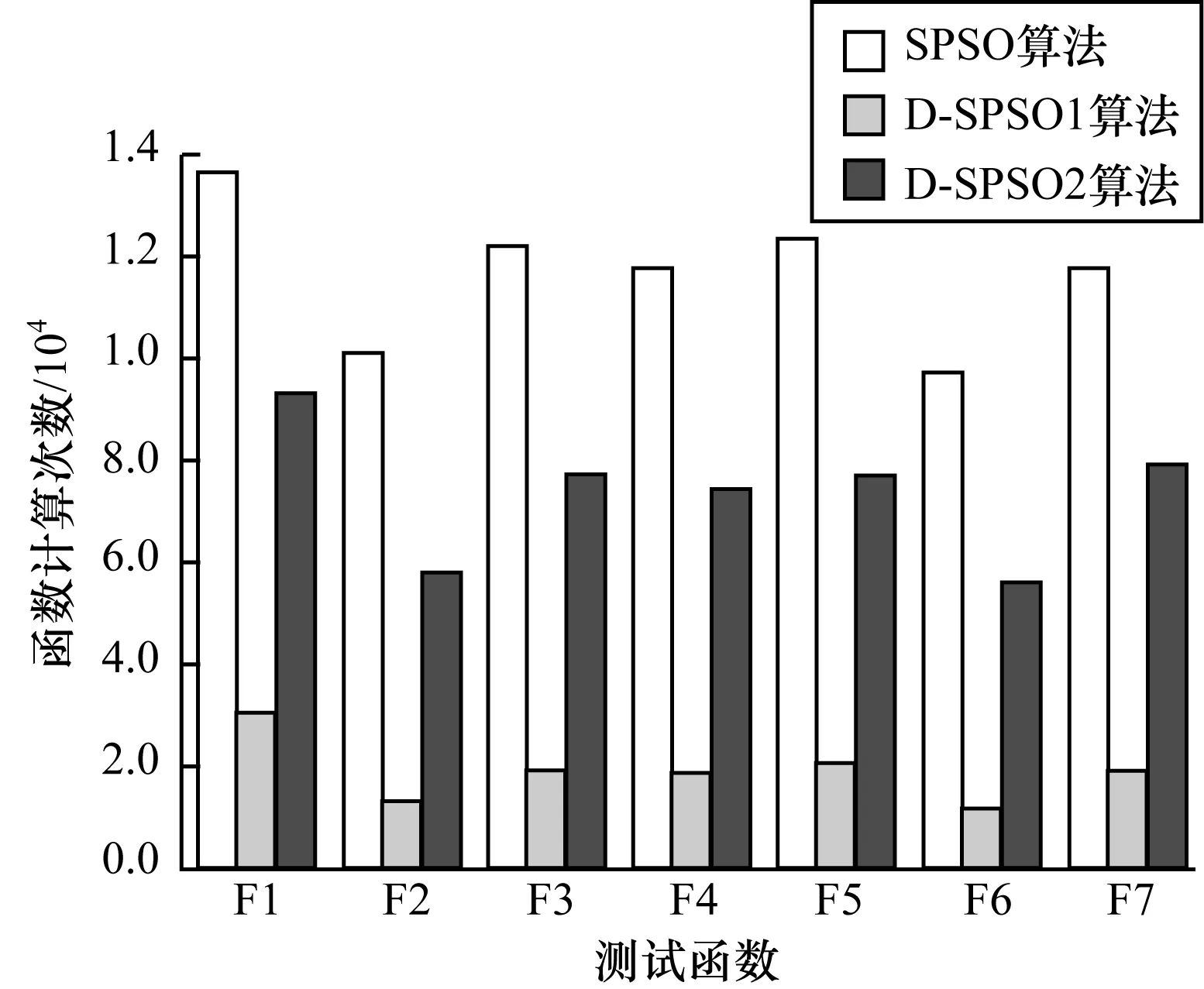
图2 SPSO与D-SPSO测试函数平均计算次数
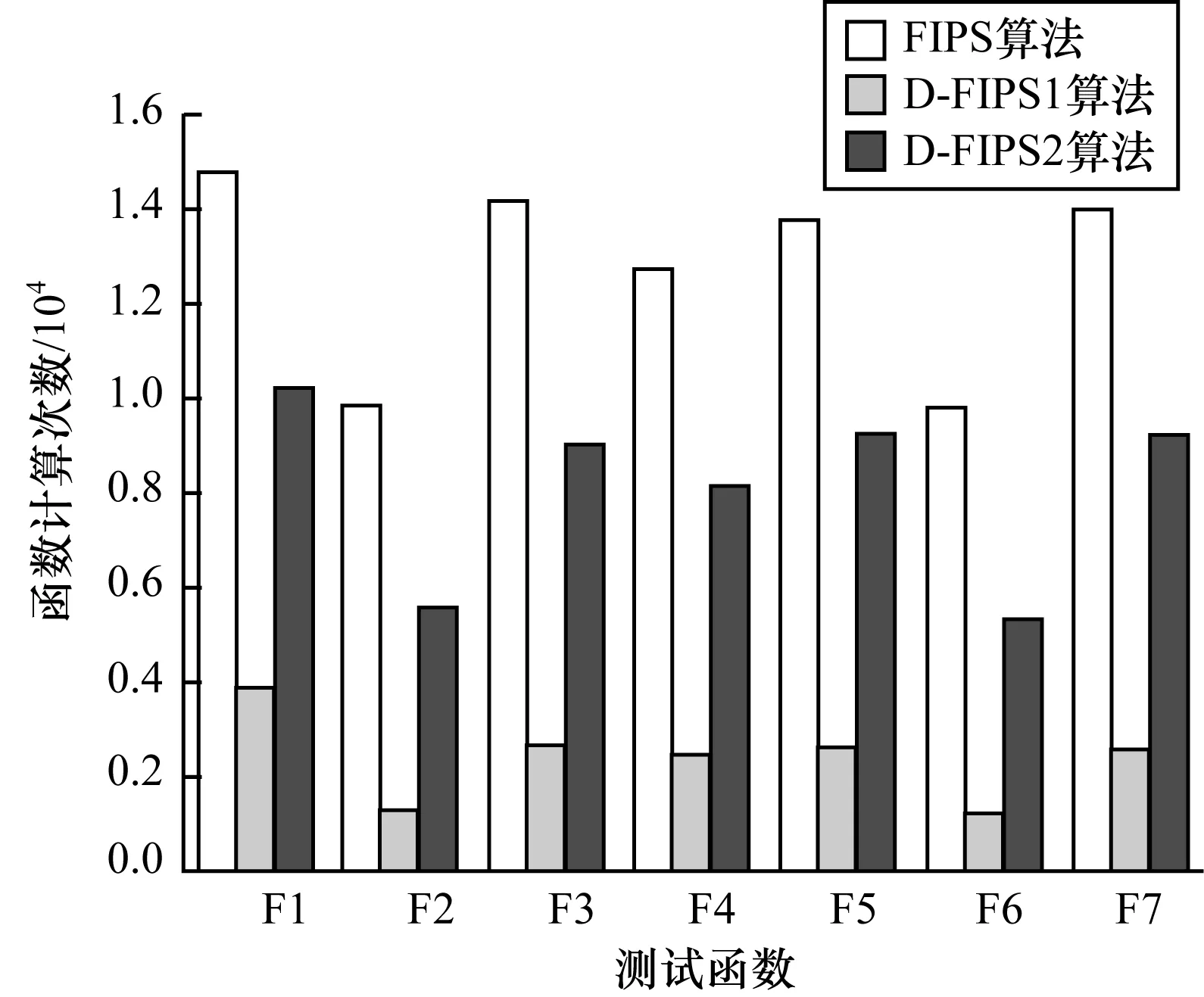
图3 FIPS与D-FIPS测试函数平均计算次数
3.2.3 优化成功率分析
表5、表6记录了各算法的函数计算次数和收敛成功率。其中,Fe表示算法在固定函数迭代次数内满足阈值所需的平均函数计算次数,反映了收敛速度的快慢,SR表示算法成功收敛试验次数占总试验次数的比例。算法SPSO、D-SPSO1和D-SPSO2的平均函数计算次数分别为116 745、19 466和73 826,平均收敛成功率分别为76.19%、84.76%和80.48%。算法FIPS、D-FIPS1和D-FIPS2的平均函数计算次数分别为127 772、24 210和81 170,平均收敛成功率均为100%。证明D-SPSO和D-FIPS不仅能以很少的函数计算次数达到寻优精度要求,同时也能取得较高的成功率,说明微分控制策略不仅提高了优化速度也能够避免陷入局部最优,具有良好的优化效率。

表5 仿真所需函数计算次数及成功率1

表6 仿真所需函数计算次数及成功率2
3.2.4 优化过程曲线
为了更加直观地反映各算法的搜索特性,对SPSO和FIPS分别选择不同的测试函数,与相应的微分控制策略改进算法进行比较。从图4~图7可以看出,微分策略在保证足够的寻优精度条件下,能够加快种群寻优速度,提高优化效率,同时对于采用不同Kd的微分策略,在不同时期微分作用的强弱对取得不同的进化速度有明显差异。

图4 Sphere函数收敛曲线
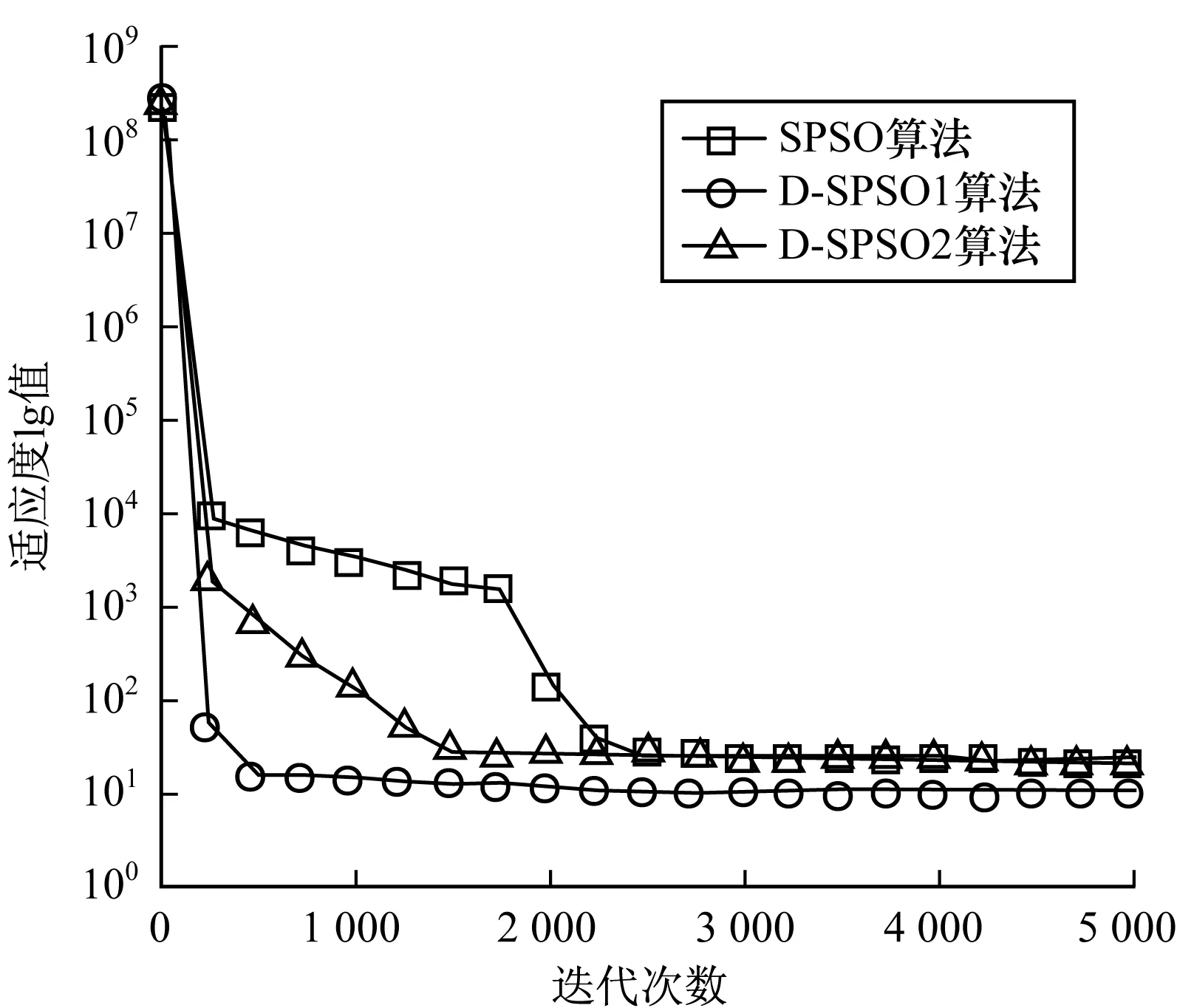
图5 ShiftedRosenbrock函数收敛曲线
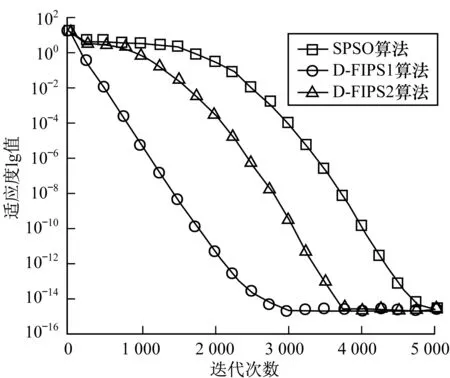
图6 Ackley函数收敛曲线
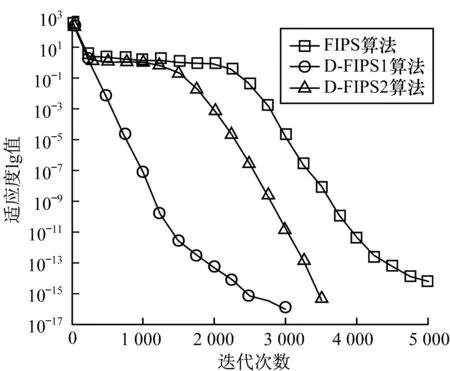
图7 RotatedGriewank函数收敛曲线
4 结束语
本文通过对粒子群优化算法进行轨迹分析,认为其搜索过程为比例-积分(PI)控制策略,通过在标准粒子群及其改进算法中引入微分项,提出微分控制策略的快速粒子群算法。通过对D-SPSO和D-FIPS进行仿真实验对比,认为微分控制策略的改进算法在解决大多数测试函数时能达到预设寻优精度,并且其函数计算次数少、寻优速度快。证明了引入该策略的改进粒子群优化算法在解决进化过程中出现的寻优效率低和寻优速度慢的问题上,取得了良好的效果,而且该策略不仅适用标准粒子群算法,对于改进优化算法也有较好的效果,对大多数粒子群算法都具有适用性,具有良好的应用拓展性。
[1] KENNEDY J,EBERHART R.Particle Swarm Optimization[C]//Proceedings of the 4th IEEE International Cofference on Neural Netwoks.Washington D.C.,USA:IEEE Press,1995:1942-1948.
[2] RATNAWEERA A,HALGAMUGE S K,WATSONH C.Self-organizing Hierarchical Particle Swarm Optimizer with Time-varying Acceleration coefficients[J].IEEE Transactions on Evolutionary Computation,2004,8(3):240-255.
[3] LIANG J J,QIN A K,SUGANTHAN P N,et al.Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Multimodal Functions[J].IEEE Transactions on Evolutionary Computation,2006,10(3):281-295.
[4] KENNEDY J,MENDES R.Population Structure and Particle Swarm Performance[C]//Proceedings of the Evolutionary Computation Congress.Washington D.C.,USA:IEEE Press,2002:1671-1676.
[5] CUI Zhihua,CAI Xingjuan.Integral Particle Swarm Optimization with Dispersed Accelerator Information[J].Fundamenta Informaticae,2009,95(4):427-447.
[6] 蔡星娟,崔志华,曾建潮,等.自适应PID控制微粒群算法[C]//第二十六届中国控制会议论文集.北京:[出版者不详],2007.
[7] ZHANG J,YANG S.A Novel PSO Algorithm Based on an Incremental PID Controlled Search Strategy[J].Soft Computing,2016,20(3):991-1005.
[8] 于海生.计算机控制技术[M].北京:机械工业出版社,2007.
[9] ZHANG Wei,LIU Jiao,FAN Lübin,et al.Control Strategy PSO[J].Applied Soft Computing,2016,38(3):75-86.
[10] MENDES R,KENNEDY J,NEVES J.The Fully Informed Particle Swarm:Simpler,Maybe Better[J].IEEE Transactions on Evolutionary Computation,2004,8(3):204-210.
[11] 韩 璞,孟 丽,王 彪,等.粒子群算法中粒子轨迹特性研究[J].计算机仿真,2015,32(12):235-240.
[12] 张 玮,王化奎.粒子群算法稳定性的参数选择策略分析[J].系统仿真学报,2009,21(14):4339-4344,4350.
[13] 李 宁,孙德宝,邹 彤,等.基于差分方程的PSO算法粒子运动轨迹分析[J].计算机学报,2006,29(11):2052-2060.
[14] SHI Yuhui,EBERHART R.Parameter Selection in Particle Swarm Optimization[C]//Proceedings of International Conference on Evolutionary Programming.Berlin,Germany:Springer,1998:591-600.
[15] LIM W H,ISA M N A.Adaptive Division of Labor Particle Swarm Optimization[J].Expert Systems with Applications,2015,42(14):5887-5903.
[16] 王永贵,林 琳,刘宪国.基于CGA和PSO的双种群混合算法[J].计算机工程,2014,40(7):148-153.

