基于异构多核系统的混合关键任务调度算法
赵瑞姣,朱怡安,李 联
(西北工业大学 a.计算机学院; b.软件与微电子学院,西安 710072)
0 概述
面对嵌入式系统功能需求的复杂化和多样性,目前多核系统已基本取代单核系统,以更好地满足系统的需要。此外,将不同关键级的任务整合到一个普通的计算平台进行更优调度,已经吸引了包括工业界和学术界在内很多专家的高度重视。在混合关键系统[1]中,设计者考虑到成本和能耗等问题将系统分为不同的运行级别,在要求不高的情况下,系统运行在非关键等级,此时,不论是成本还是能耗都比较低。但是当系统处于某种特殊情况时,为了确保其安全性,需要提高系统的关键级。当前很多认证标准如自动化领域的ISO标准[2]以及航空电子领域的DO-178C标准[3]等都根据每个功能应具备的安全程度明确规定了关键级别。
此外,随着异构多核系统[4]的兴起,异构的多核处理器以其优于同构多核处理器的性能被广泛应用在很多的控制领域,包括航天控制、遥感控制等。然而目前多数混合关键系统(Mixed-Criticality System,MCS)任务调度问题都是在同构多核的基础上被提出,未全面考虑异构多核的特性。为此,本文针对异构多核系统的相关特性,提出一种混合关键任务调度算法。
1 研究现状
文献[5]提出了混合关键系统MCS的概念,并同时运用一种形式化的方法对这一概念进行了定义,此后关于MCS的研究成为一个非常热门的方向。文献[6]建立了自适应混合关键模型AMC。在该模型中,当系统升级为高关键级别时,所有的低关键级的任务都会被直接丢弃,这虽然保证了高关键级任务的CPU执行时间,但是却完全忽略了低关键级任务的执行,由于所有任务都以最坏执行时间作为调度依据,而在大部分情况下都达不到最坏情况,因此这种在关键级切换过程中将低关键级任务直接丢弃的做法是极其不合理的。而且对于一些应用来说,偶尔的延时[7]是可以被接受的,这些延时任务的执行结果仍有参考价值。为了弥补AMC任务处理过程的不足,适当地考虑给低关键级任务提供一定等级的服务质量,文献[8]提出了一种类似弹性任务模型的处理机制,当系统处于高关键级时,它会调整低关键级任务的周期,但该方法是基于固定优先级的任务调度,不能实现系统的动态调度[9-10]。而由于混合关键系统处于不同关键级别时优先顺序可能发生改变,因此从这方面而言,该方法不再适用。
文献[11]给出了一种对于混合关键系统中低关键任务的优先级定义方法。对低关键任务进行服务等级的划分,通过服务等级的重新划分,大幅增加低关键任务的调度公平性[12],使得对低关键任务的调度更加合理。但是该方法并没有考虑如何提高关键任务的调度成功率,同时也没有考虑处理器负载情况。为在关键级提升时保证高关键级任务的正确执行,文献[13]提出了MCPI算法,在关键级提升时对任务的优先级进行重新分配,将高关键任务的优先级提高,以便能优先执行高关键任务。该方法在很大程度上降低了关键任务的丢失率,提高了系统的安全性,但是对低关键级任务只是采用了best-effort处理,没有充分利用任务执行过程中的slack时隙[14],降低了对低关键任务的接受能力。
针对混合关键系统的任务调度特点,文献[15]提出了一种双分区的调度策略,在系统处于不同的关键级别时重新对非关键任务进行处理器的映射。但该方法仅考虑了非关键任务的重新分配以及核间迁移,在非关键任务的迁移过程中没有考虑利用任务执行过程中的slack时隙进行非关键任务的处理,所以,该方法仍有很大的改进空间。
基于上述方法的不足,本文提出一种基于异构多核系统的混合关键任务调度算法。对文献[15]中DPM算法进行扩展与改进,去除不允许高关键任务核间迁移的限制。将混合关键任务的调度分为处理器映射以及系统模式切换处理2个阶段。在处理器映射阶段,优先将关键任务分配到强核上进行处理同时以处理器最大剩余带宽为指标,运用启发式方法进行任务分配,采用EDF算法[16]进行单处理器上的任务集调度,从而最大化处理器的利用率。此外,引入回收队列,完成对非关键任务的回收再分配,更好地利用slack时隙,使混合关键任务调度过程中关键任务和非关键任务的调度成功率都有所提高。
2 异构多核系统与任务模型
本文算法采用双关键级任务模型。需要强调的是,由于最终要完成异构多核处理器上的混合关键任务调度,因此在保证关键任务截止期要求的同时也要最大限度地提高非关键任务的调度成功率,同时还要考虑异构多核的负载均衡能力。
2.1 异构处理器模型
异构处理器与同构处理器的不同表现为CPU处理能力的非对称性,每个处理器在未分配任务时,均有一个初始的资源利用率带宽。本文中对异构处理器做出如下定义:
定义1异构处理器模型表示为C={C1,C2,…,Cm},其中,m表示系统中处理器核数,Ci表示的是第i个处理器的单位时间的计算能力,由于异构并行系统中不同核具有不同的计算能力,因此Ci的值也会有所不同。
定义2异构系统中各个核的计算能力不同,因此,每个任务的处理时间因处理器的不同而变化,可用矩阵M表示如下:
其中,ti(i,j)表示任务i在处理器j上的执行时间。
定义3对于每个处理器都会有剩余的计算带宽,即每个处理器的最大剩余可用利用率。系统的剩余利用率可用U={U1,U2,…,Um}表示,其中Ui为第i个处理器的剩余计算带宽。
2.2 任务模型
本文研究的是双关键级模式的混合任务在异构处理器上的调度问题,因此,对以往的任务模型做适当修改,给出以下定义:
定义4对于每一个任务,可由五元组表示为{Li,S,Ci(LO),Ci(HI),Ti(LO),Ti(HI)},其中,S是任务的释放时间,即到达时间,Li∈{LO,HI}表示任务i所处的关键级别,Ci(LO)表示任务wi在LO模式下的最坏执行时间,Ci(HI)表示任务wi在HI模式下的最坏执行时间,Ti(LO)、Ti(HI)分别表示任务wi在非关键LO模式和关键HI模式下的周期。其中Ci(LO)和Ci(HI)是一个m维向量元素,分别表示任务在不同的处理核上的最坏执行时间,其值与计算能力成反比。同时处于2种不同模式下的任务的最坏执行时间和周期满足以下关系:当Li=LO时,Ci(LO)=Ci(HI),Ti(LO)≤Ti(HI);当Li=HI时,Ci(LO)≤Ci(HI),Ti(LO)=Ti(HI)。从上式可以看出,当系统从非关键LO模式转换为关键HI模式时,降低了对非关键任务的服务质量。
定义5每一个任务wi有2个带宽利用率,用二元组(ui(LO),ui(HI))表示,其中,ui(LO)=Ci(LO)/Ti(LO),ui(HI)=Ci(HI)/Ti(HI)。
定义6如果每一个任务都能在其死限之前完成,那么该任务可调度;如果一个任务集中的所有任务都能在死限前完成,那么该任务集可调度。

3 异构混合关键任务调度算法
3.1 调度模型
为了充分利用异构并行系统的特性,同时考虑到运用计算能力强的核来处理关键任务可以使其更快更好地完成,本文将异构处理器模型进一步表示为C={πq,πr},其中πq代表强核集,即Ci>1的处理器构成的集合,πr代表弱核集,即Ci≤1的处理器核构成的集合,由于关键任务的死限丢失会给系统造成很严重的后果,直接关系到系统的安全性,因此此处优先考虑将其映射到强核集合上进行调度,将非关键任务映射到弱核集进行调度,并同时记录各个核的剩余负载情况U={U1,U2,…,Um},当任务到来时优先考虑将任务分配到剩余负载较高的核上调度。图1为本文算法的调度模型,其中虚线箭头表示对不能直接调度的任务的重新分配再调度。
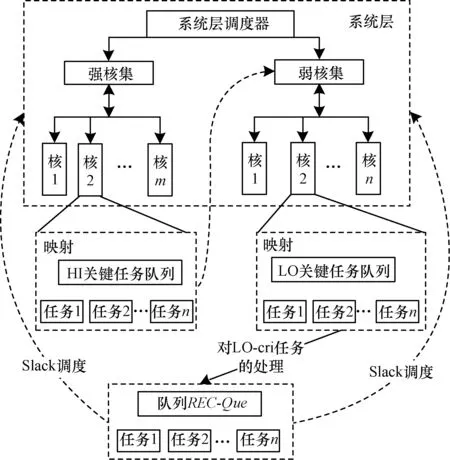
图1 异构多核系统的调度模型
为使关键任务能有效地利用强核的计算能力,保证系统的安全性,在异构多核的调度过程中始终坚持以下原则:1)每个任务都是独立执行的;2)忽略核间迁移和级别切换的开销;3)同一时刻一个任务只能在一个核上执行。
3.2 算法实现
本文算法考虑异构多核中CPU的执行能力不同的特性以及关键任务和非任务的核间迁移,并且对于被迫中止执行的非关键任务采取回收再调度的策略,一方面为关键任务提供了更多的执行时间和更优的服务质量,保证系统的安全;另一方面也弥补了直接将非关键任务丢弃的不足,降低了非关键任务的死限丢失率。
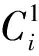
阶段1异构处理器的映射阶段
1)对于m个异构处理器C={πq,πr},πq={C1,C2,…,Cm1},其中,Ci>1,1≤i≤m1,πr={C1,C2,…,Cm2},其中,Cj≤1,1≤j≤m2,HI-Que={w1,w2,…,wn1},LO-Que={w1,w2,…,wn2},系统关键级ζ∈{HI,LO},初始值为LO,REC-Que=Ø,利用率U={U1max,U2max,…,Ummax}。
2)若HI-Que≠Ø,将HI任务wi按照死限时间(默认T)递增的顺序进行排序,作为任务调度的优先级,跳转至步骤4)。
3)若LO-Que≠Ø,LO任务wi按照死限时间(默认T)递增的顺序进行排序,作为任务调度的优先级,跳转至步骤4);否则,跳转至步骤5)。
4)∀wi∈HI-Que,若∃Uj>0,1≤j≤m1,则将wi按照计算的优先级顺序在πq中选择U最大的核Cj进行处理,若调度成功,更新Ujmax=Ujmax-Ci(i,j)/Ti(LO),若不能成功调度,将系统关键级升高,即更新ζ=HI,进入阶段2。
5)∀wi∈LO-Que,若Uj>0,1≤j≤m2,将wi依据优先级先后分配给πr中利用率U最大的核Cj调度,调度成功,更新Ujmax=Ujmax-Ci(i,j)/Ti(LO),否则,关键级提升,更新ζ=HI。
6)退出算法。
阶段2系统关键级切换的处理阶段
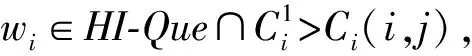
2)当ζ=HI时,∃wi∈HI-Que∩wiπq,此时进行强核集πq中HI任务的重新分配,直至任务可以调度。
3)若步骤2)不成立,将HI任务wi映射到弱核集πr中进行调度,并强行中止利用率U最大的核上的LO任务的执行,进行HI任务的调度,计算该核的剩余利用率Ujmax=Ujmax-Ci(i,j)/Ti(HI)+Cj(i,j)/Tj(HI),并同时将被终止的任务wj∈LO-Que在πr中其他核心进行重分配,若分配失败,跳转至步骤4)处理。
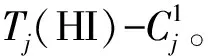

3.3 算法复杂度分析
对于每一个关键任务来说,最好情况是一次性成功映射到强核集中的某个处理器并成功在该核调度,复杂度为O(1),最坏情况是遍历完整个强核集都没能成功调度,此时在弱核集中抢占非关键级任务的执行时间来执行,时间复杂度是O(m1+1),其中m1表示强核集的CPU个数。所以,对全部的关键任务调度的复杂度为O((m1+1)×n1),n1表示关键任务的数量。
对于非关键任务来说,在弱核集的某个处理器上调度成功的最小复杂度为O(1),最大时间复杂度为O(m2),其中m2为弱核集的CPU个数。当其不能在弱核集中成功调度时,将其暂时存放入REC-Que回收队列,以便进行一个利用空闲时间的全局调度,此时时间复杂度为O(m×n2′),其中n2′表示回收队列中的非关键任务数量。对于有n2个非关键任务的调度的复杂度为O(m2×n2)。综上所述,算法的总复杂度可表示为O(n1×(m1+1)+m2×n2+m×n2′)。可以看出,算法复杂度与异构处理器核的处理能力和数量、关键任务与非关键任务的个数有直接关系,并且该复杂度在可接受的范围内。
4 仿真实验
仿真实验依据文献[15]方法进行。仿真实验均基于以下假设:处理器核数为4,调整其中2个核的频率为1 GHz,另外2个核心频率为1.5 GHz,系统的整体CPU资源利用率区间为[1.0,3.8],对于实验中非关键任务的周期T(LO),随机从{10,20,40,50,100,200,400,500,1 000} ms中选取,为保证系统关键级提升后的周期约束关系,即Ti(LO)≤Ti(HI),此处假设T(HI)=2×T(LO)。当系统处于非关键LO模式下,每个任务的最坏执行时间Ci(LO)为0.2~0.8倍的任务周期T(LO),且保证Ci(HI)=2×Ci(LO)。
1)验证不同CPU利用率下算法的调度成功率。
实验方案:控制实验数据中关键任务数量与非关键任务数量的比值为1∶1,并随机生成1 000个实验任务集,每个任务集中包括10个~20个相互独立的任务来进行实验,并对实验数据进行平均。图2展示了本文算法与DPM算法[13]的对比结果,从中可以看出,在系统处于相同CPU利用率的情况下,本文算法有更高的任务接受能力,尤其是当系统利用率越高时,本文算法可以接受更多的任务。

图2 CPU利用率与任务接受能力的关系
2)验证不同任务数情况下算法的可靠性。
实验方案:控制实验数据中关键任务数量与非关键任务数量的比值为1∶1,并且设定每个核的CPU利用率为85%,同时使任务集中的任务数量在20~100中均匀分布,以此为输入进行验证,图3展示了实验结果。可以看出,随着任务集中任务数量的不断增多,本文算法的任务丢失率明显低于DPM算法,并且在任务数量增加时对任务的接受能力趋于稳定。
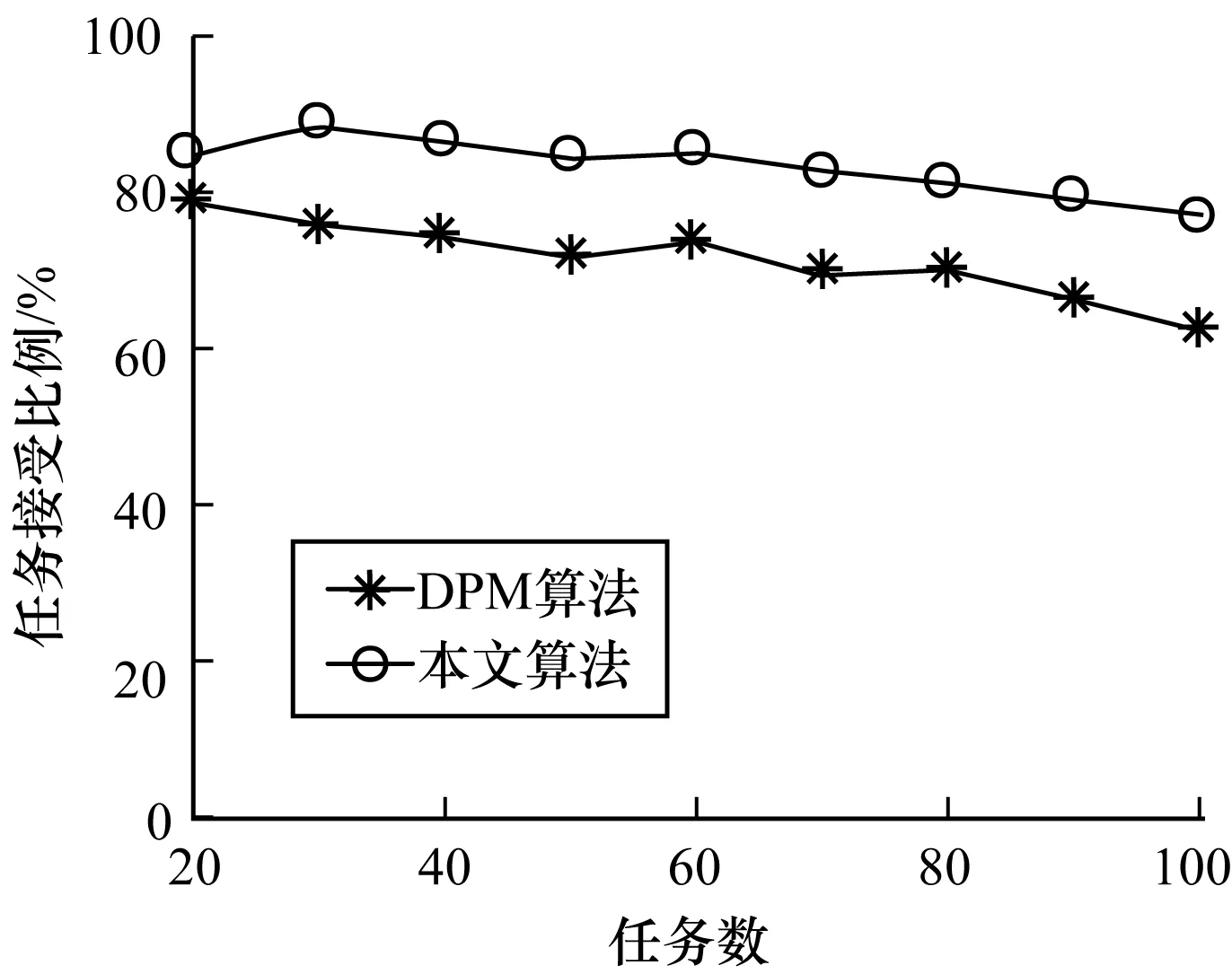
图3 任务数与任务接受能力的关系
3)验证关键任务和非关键任务的比例发生变化时,算法是否能保持优越性。
实验方案:将任务集中2种任务所占百分比在20%~70%之间进行调整,实验的结果如图4所示。可以看出,当关键任务占比小于30%时,使用不同的算法对任务可调度性的影响并不大,但是随着关键任务占比的不断增加,本文算法可以很大程度上提高系统对任务的接受能力,这主要是因为DPM算法并没有考虑关键任务的核间迁移。
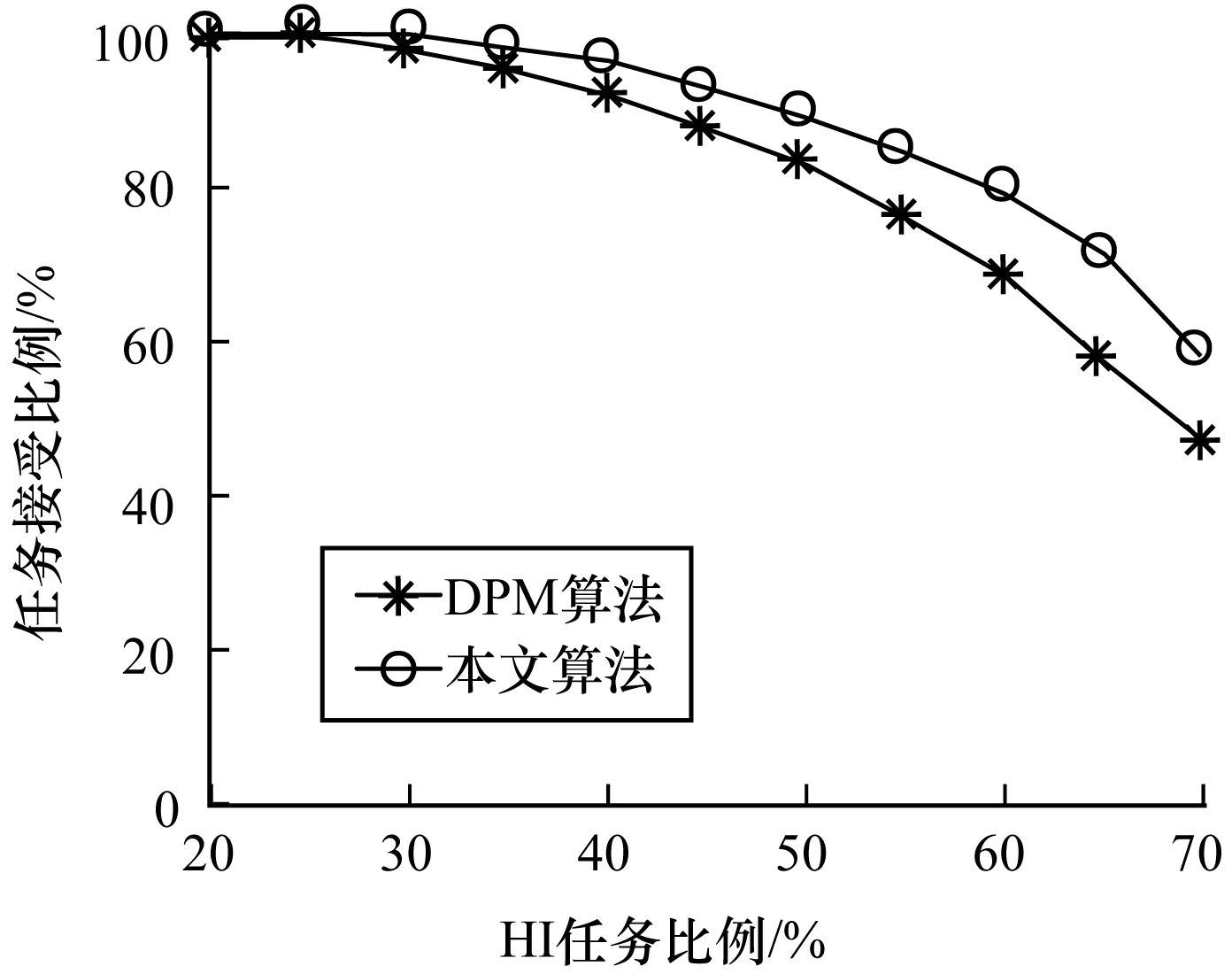
图4 HI任务比例与任务接受能力的关系
5 结束语
针对异构多核特性以及混合关键任务调度过程中存在的问题,本文提出一种更适用于异构多核系统的混合关键任务调度算法。从2个方面着手进行任务调度,首先将关键任务和非关键任务划分为不同的集合进行处理器映射,综合考虑异构处理器的特性尽量将关键任务优先分配给计算能力强的核,并且允许任务的核间迁移,保证系统的安全;其次考虑在系统关键级切换时对于非关键任务的处理,本文对于被迫中止的非关键级任务并没有采用直接丢弃的处理方式,而是将其回收,并采用全局的调度策略,通过任务执行过程中的空闲时隙进行调度,从而提高对低关键级任务的接受能力。仿真实验结果表明,本文算法可有效提高系统任务接受能力。下一步将从关键级切换时间以及核间迁移时间出发对该算法进行扩展,提高其精确度与实用性。
[1] BURNS A,DAVIS R.Mixed Criticality Systems-A Review[D].York,UK:University of York,2013.
[2] HEFFERNAN D,MACNAMEE C,FOGARTY P.Runtime Verification Monitoring for Automotive Embedded Systems Using the ISO 26262 Functional Safety Standard as a Guide for the Definition of the Monitored Properties[J].IET Software,2014,8(5):193-203.
[3] MOLLISON M S,ERICKSON J P,ANDERSON J H,et al.
Mixed-criticality Real-time Scheduling for Multicore Systems[C]//Proceedings of IEEE International Conference on Computer and Information Technology.Washington D.C.,USA:IEEE Press,2010:1864-1871.
[4] 姚丽莎,王占凤,程家兴.基于人工鱼群遗传算法的异构多核系统任务调度研究[J].计算机工程与科学,2014,36(10):1866-1871.
[5] VESTAL S.Preemptive Scheduling of Multi-criticality Systems with Varying Degrees of Execution Time Assurance[C]//Proceedings of RTSS’07.Washington D.C.,USA:IEEE Press,2008:239-243.
[6] BARUAH S K,BURNS A,DAVIS R I.Response-time Analysis for Mixed Criticality Systems[C]//Proceedings of RTSS’11.Washington D.C.,USA:IEEE Press,2011:34-43.
[7] YIP E,KUO M,BROMAN D,et al.Relaxing the Synchronous Approach for Mixed-criticality Systems[C]//Proceedings of the 20th IEEE Real-time and Embedded Technology and Application Symposium.Washington D.C.,USA:IEEE Press,2014:89-100.
[8] BURNS A,BARUAH S.Towards a More Practical Model for Mixed Criticality Systems[EB/OL].[2016-05-10].http://www-users.cs.york.ac.uk/~robdavis/wmc2013/paper3.pdf.
[9] 刘 怀,费树岷.基于双优先级的实时多任务动态调度[J].计算机工程,2005,31(18):16-18.
[10] SU Hang,ZHU Dakai,MOSSE D.Scheduling Algorithms for Elastic Mixed-criticality Tasks in Multicore Systems[C]//Proceedings of IEEE International Conference on Embedded and Real-time Computing Systems and Applications.Washington D.C.,USA:IEEE Press,2013:352-357.
[11] HIKMET M,KUO M M,ROOP P S,et al.Mixed-criticality Systems as a Service for Non-critical Tasks[C]//Proceedings of IEEE International Symposium on Real-time Distributed Computing.Washington D.C.,USA:IEEE Press,2016:221-228.
[12] 王 涛,安 虹,孙 涛,等.面向动态异构多核处理器的公平调度算法[J].软件学报,2014,25(S2):80-89.
[13] SOCCI D,POPLAVKO P,BENSALEM S,et al.Multiprocessor Scheduling of Precedence-constrained Mixed-critical Jobs[C]//Proceedings of International Symposium on Real-time Distributed Computing.Washington D.C.,USA:IEEE Press,2015:198-207.
[14] 朱怡安,黄姝娟,段俊花,等.新的混合关键任务调度算法的研究[J].电子科技大学学报,2014,43(2):268-271,286.
[15] AL-BAYATI,Z,ZHAO Qingling,YOUSSEF A,et al.Enhanced Partitioned Scheduling of Mixed-criticality Systems on Multicore Platforms[C]//Proceedings of ASP-DAC’15.Chiba,Japan:[s.n.],2015:630-635.
[16] LEE J.New Response Time Analysis for Global EDF on a Multiprocessor Platform[J].Journal of Systems Architecture,2016,65:59-63.

